钢结构螺栓节点力学特性敏感性分析

摘 要：钢结构螺栓节点受力特性一直是相关领域研究的重点和难点。本文通过试验和数值模拟手段对其进行研究，并对比了试验结果和数值模拟结果的差异。结果表明：与试验结果相比，数值模拟结果在数值和变化趋势上都较为接近，差幅在5%内，证明本文建立的有限元数值模型是合理、有效的。刚度比参数对螺栓节点的影响主要体现在数值方面，并不改变其随转角的变化趋势。节点弯矩与刚度比呈现负相关关系，随刚度比增加而减少。转角弯矩随钢材屈服刚度增加而减少，且位移持续减少。垫板厚度对螺栓节点弯矩影响较小，主要体现在垫板区域的受力分布方面。

关键词：钢结构；螺栓节点；刚度比；数值模拟

中图分类号：TU 39 " 文献标志码：A

随着我国基建行业的发展和城市化的推进，大跨度钢结构工程项目越来越多。因此，针对钢结构的力学特性和相关设计，许多研究人员进行了一系列研究。

丁文其等[1]提出了波纹钢结构N-M-T（轴力-弯矩-温度）曲面，对波纹钢结构在高温下的压弯性态进行了研究。徐言等[2]提出一种膜材自动脱落装置的概念构造设计，并利用数值计算方法探究了装置夹角和抗拔深度对承载力的影响。谢甫哲等[3]对复杂空间钢结构多点同步提高施工与监测技术进行了研究，分析了同步提高和不同步提高情况下结构的受力状态。杨雪等[4]基于midas Gen软件建立结构整体单尺度模型及包括关键节点的多尺度模型，探讨了结构的稳定性、动力响应等力学性能。赵跃港等[5]采用有限元数值模拟工具分析了3种不同施工方案，对比了不同方案对主体钢结构受力、变形及支撑结构最大支反力的影响。刘勇等[6]采用数值模拟手段分析了地震荷载作用下不同节点的受力情况及结构动力特性。

本文对室内模型试验和数值模拟进行了研究。通过室内试验数据验证了模型的有效性，并根据已验证的模型对影响钢结构螺栓节点力学性能的因素进行了分析和讨论。

1 试验概况

本文研究对象为钢结构新型柱-柱螺栓节点，内框架柱下端的方形槽内结构由上至下依次为定位板、定位筒以及下端板。在下部模块中，内框架柱上端的方形槽内则焊接有多个上端板，并设置垫块于上下模块之间（图1）。梁柱截面尺寸均为150mm×150mm×8mm，其中，梁长度为1.5m，柱长度为1m，均为冷弯方钢管柱。垫板和上端板厚度均为30mm，下端板厚度为15mm，斜加劲肋厚度为10mm。螺栓为45号钢，其余材料钢材均为Q235B，焊缝为E43。表1为钢材的力学参数。

为探究柱在轴压作用下内置螺栓节点的抗弯性能，本文进行抗弯试验研究。试验对象由四梁四柱连接而成，采用液压千斤顶在梁两端进行同步对称加载，加载方式由荷载控制。通过施加恒定压力于柱顶模拟柱轴力，将轴压荷载设为540kN。

2 有限元数值模型

2.1 模型建立

采用有限元数值模拟软件进行三维建模，根据试验数据对模型有效性进行验证，对内置螺栓节点性能以及主要影响因素进行探究。

根据室内试验结果对钢材力学计算参数进行取值，将泊松比设为0.3，摩擦系数为0.2，屈服条件遵循mises屈服准则。当进行网格划分时，对螺栓节点进行局部网格加密处理，共划分93427个10节点有限元网格，图1为该有限元模型的网格划分情况。

在建模过程中，为提高计算效率，同时不影响计算精度，可以忽略定位板和定位筒设定，同时，将上端板设置为3块，下端板为1块。在接触条件方面，将下端板与螺栓的接触条件设置为滑移接触，通过绑定连接模拟焊缝连接。在边界条件方面，施加平面外约束于梁侧面，通过预紧力固定螺栓，固定后在每个柱施加267kN的轴力，梁两侧加载方式为位移控制，加载位移为100mm。

2.2 模型验证

图2为梁节点弯矩随转角的变化曲线对比情况。从图中可以看出，在试验工况中，当转角小于0.02rad时，随着梁转角增加，节点弯矩呈现线性增加变化趋势，当转角超过0.02rad时，弯矩随转角增加速率大幅下降，增加速度较为缓慢，表明此时材料已进入强化阶段，其峰值弯矩达到172.4kN∙m，对应的转角约为0.04rad。

与试验结果相比，数值模拟结果在数值和变化趋势上都较为接近，说明本文建立的钢结构螺栓节点力学分析模型的合理、有效性。在进入强化阶段后，弯矩数值模拟计算结果比试验结果略大，在转角为0.04rad的工况下，弯矩试验结果为176.7kN∙m，数值模拟计算结果为182.1kN∙m，差值约为3.1%。在数值模拟中仍存在一系列理想化假定，例如本构计算模型和变形约束条件假定以及未考虑材料的各向异性等，但整体而言，数值模拟结果与试验结果差幅在5%以内。本文建立的数值模型是研究钢结构螺栓节点力学特性的有效工具。

3 结果分析与讨论

采用研究模型对钢结构螺栓节点力学性能的影响因素进行探究，包括上下梁刚度比、钢材屈服强度和垫板厚度，并对其进行对照模拟。初始条件的上下梁刚度比为1.0、钢材屈服强度为309MPa，垫板厚度为30mm。

3.1 刚度比影响

图3为5种不同地板梁、天花板梁刚度比工况下钢结构螺栓节点的转角-弯矩变化曲线。从图中可以看出，不同刚度比工况下的节点弯矩随转角的变化趋势基本一致，当前期转角小于0.02rad时，随着梁转角增加，节点弯矩呈线性，当转角超过0.02rad时，曲线变缓，各工况差异主要为数值差异。随着地板梁与天花板梁刚度比增加，相同节点转角工况下的弯矩随之变小，节点弯矩与刚度比呈负相关关系。在刚度比为1.0的工况下，转角0.02rad时对应的节点弯矩为251.2kN∙m，在刚度比为1.5的工况下，转角0.02rad时对应的节点弯矩为228.1kN∙m，比前者减少了9.2%；在刚度比为2.0工况下，转角0.02rad时对应的节点弯矩为204.3kN∙m，比前者减少了10.4%，在刚度比为2.5的工况下，转角0.02rad时对应的节点弯矩为184.5kN∙m，比前者减少了9.7%，在刚度比为3.5的工况下，转角0.02rad时对应的节点弯矩为154.7kN∙m，比前者减少了16.2%。

表2为5种工况下初始抗弯强度、屈服弯矩和塑性弯矩的变化情况。从表2可以看出，增加地板梁与天花板梁的刚度比会使节点的抗弯承载力明显提高，但与此同时，随着地板梁高度增加，下柱的塑性区范围也随之变大，会对结构安全造成影响。

3.2 屈服强度影响

图4为两种不同钢材屈服强度工况下的节点转角-弯矩曲线，分别为Q235钢和Q345钢，屈服强度分别为309MPa和400MPa。从图中可以看出，随着钢材屈服强度增加，相同转角位移条件下转角弯矩减少，钢材屈服强度与节点弯矩呈负相关关系。同时，钢材弹性变化阶段亦存在差异，随着钢材屈服强度增加，节点转角-弯矩线性变化阶段持续位移减少，即当位移较小时，节点弯矩就达到稳定状态，随着节点转角增加弯矩增加缓慢或不再增加。在Q235钢材工况下，节点弯矩峰值达到了226kN∙m。在Q345钢材工况下，节点弯矩峰值为178kN∙m，比前者降低了21.2%，由此可见，钢材屈服强度对螺栓节点力学性能也有较为明显的影响。

表3为2种工况下初始抗弯强度、屈服弯矩和塑性弯矩的变化情况。从表3可以看出，两种工况下螺栓节点初始抗弯刚度完全一致，主要差异在节点屈服弯矩和塑性弯矩方面。在Q235钢材工况下，螺栓节点屈服弯矩为151.4kN∙m，塑性弯矩为176.8kN∙m，在Q345钢材工况下，螺栓节点屈服弯矩为212.6kN∙m，塑性弯矩为227.6kN∙m，比前者分别增加了40.4%和28.4%。这也验证了上述分析结论，即钢材屈服强度对螺栓节点力学性能也有较为明显的影响，具体体现在屈服弯矩和塑性弯矩方面。

3.3 垫板厚度的影响

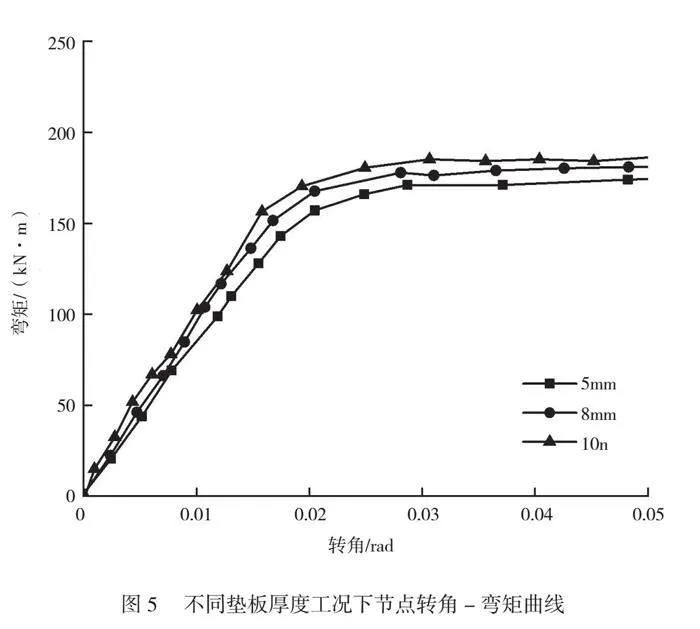
图5为不同垫板厚度工况下的节点转角-弯矩曲线。从图中可以看出，与上下梁刚度比和屈服强度相比，垫板厚度影响较小。在3种工况下，螺栓节点弯矩随转角变化趋势基本一致，先线性增加后逐步稳定，主要差异为数值差异。在相同转角条件下，垫板厚度越大对应的节点弯矩越大，同时节点刚度、屈服弯矩和塑性弯矩也越大，但差异较小。表明垫板厚度主要是对垫板区域的受力情况有较为明显的影响。

4 结论

为研究钢结构螺栓节点力学特性和相关影响因素，本文通过加载试验和数值仿真模拟，验证了数值模型的有效性，同时对钢结构螺栓节点力学特点进行探究。得出以下结论。1）不同刚度比工况下的螺栓节点弯矩随转角的变化趋势基本一致，当转角超过0.02rad时，曲线变缓，各工况差异主要为数值差异。随着地板梁与天花板梁刚度比增加，相同节点转角工况下弯矩随之减少，节点弯矩与刚度比呈负相关关系。2）随着钢材屈服强度增加，相同转角位移条件下转角弯矩减少，钢材屈服强度与节点弯矩大小呈负相关关系。钢材弹性变化阶段亦存在差异，随着钢材屈服强度增加，节点转角-弯矩线性变化阶段位移持续减少。3）与上下梁刚度比和屈服强度相比，垫板厚度对其影响较小。垫板厚度主要是对垫板区域的受力情况有较为明显的影响。

参考文献

[1]丁文其，马畅，刘常浩，等.波纹钢结构高温压弯性态数值模拟与理论分析[J].工程机械与维修，2024（3）：11-13.

[2]徐言，王仲迪.强风作用下大跨度屋盖膜结构自动脱落装置概念设计及受力分析[J].工业建筑，2023，53（增刊2）：289-294.

[3]谢甫哲，陈丙辉，袁小军，等.复杂空间钢结构多点同步提升施工与监测技术研究[J].建筑结构，2023，53（14）：126-131.

[4]杨雪，王金龙，刘宇雄，等.基于多尺度模型大悬挑钢结构力学性能分析[J].长沙理工大学学报（自然科学版），2023，20（2）：137-145.

[5]赵跃港，贺子奇，张花杰，等.空间管桁架钢结构体育馆吊装施工方案对比分析[J].河南大学学报（自然科学版），2023，53（2）：244-252.

[6]刘勇，魏珍中，刘佳敏，等.装配式钢结构配套外挂墙板连接节点受力性能分析[J].山西建筑，2022，48（23）：10-14.