趣味数独：数对法

当一单元中某两格仅可能为两个数字时，称这两格构成数对。如果格A和格B是数对，那么它们的值仅可能是a和b（a和b是1～9之间的任何两个数字），可以将该数对记为{a，b}。

数对出现在宫里，成为宫数对；出现在行（列）中，称为行（列）数对。

根据抽屉原理，格A和格B构成数对{a，b}，格A和格B的值只能是a和b，而不可能是其他数。这就是数对有别于普通区块的重要性质，即数对的占位作用。

大部分的数对是排除的结果，通过排除法形成的数对称为排除数对；还有一部分数对是通过余数法形成的，通过余数法形成的数对称为余数数对。

下面请尝试找出下列例题的数对。

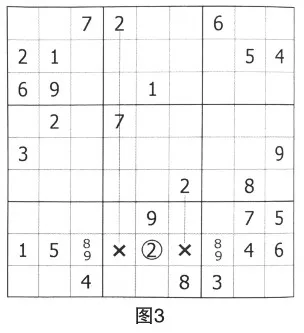
1.数对R（2，3）C3={6，8}是排除数对，是由数字6和8对第一宫排除形成的。第一宫中，空格R1C1、R1C3及R2C1排除数字6和8，因此数字6和8只能在空格R2C3和R3C3中。

2.数对R（8，9）C7={5，6}是排除数对，是由数字5和6对第九宫排除形成的。

3.数对R（8，9）C2={4，6}是余数数对。第二列中只有这两个空格，也就是说除了4和6，其他数字在第二列中已经全部出现。

4.数对R5C（4，6）={6，9}是余数数对，空格R5C4和R5C6的余数只有数字6和9。

观察下列例题，找出第八宫中空格R8C5中的数字。

注意观察第八宫，已经出现了数字8和9，故空格R8C4和R8C6中的数字排除8和9。

因此，对于第八行，存在数对R8C（3，7）={8，9}。

考虑数对R8C（3，7）的占位作用，用数字2对第八行进行排除，R8C5=2。

数对的应用主要是数对排除法、数对替代法以及数对占位法。

下面例题中，如果能发现数对，得到唯一解就比较容易了。

如下图所示，第一宫中，应用宫排除法，发现数对R（2，3）C2={1，2}。

第一步：第一宫R（2，3）C2={1，2}，应用数对占位法，R1C3=4。

数对的占位作用在这里至关重要。因为用数字4对第一宫进行排除，空格R2C2和R3C2是不能确定是否排除数字4，而数对R（2，3）C2的存在，使这两个空格排除了1和2以外的数字。

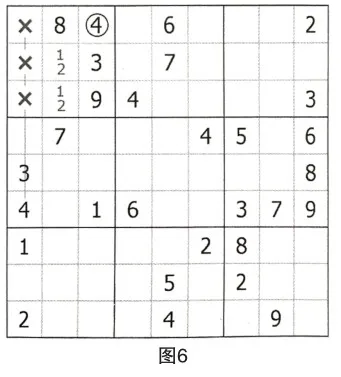
第二步：由于R（2，3）C2={1，2}，因此应用数对替代法，R6C2=5。

如果不考虑数对的作用，空格R6C2的余数就是2和5；如果考虑数对，利用其替代作用，空格R6C2的余数就仅剩下数字5。

如下图所示，用数字1对第九列进行排除，发现区块R（8，9）C9=1。

如下图所示，用数字7对第三宫进行排除，发现区块R（1，3）C7=7。

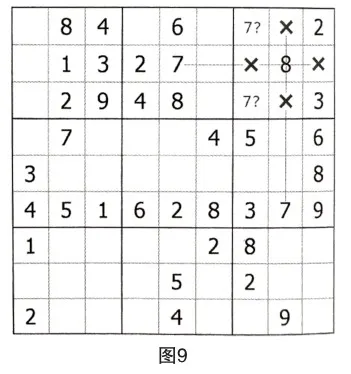
第三步：应用区块替代法，考虑到区块R（8，9）C9和R（1，3）C7的替代作用，点算空格R9C7的余数，得到R9C7=6。

进展至此，下一步的突破口应该选择哪里？

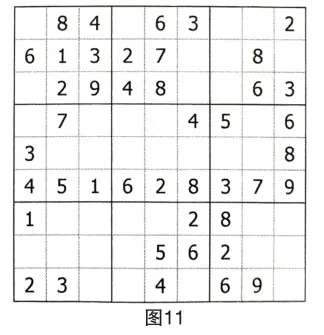
用数字5和7对第五宫进行排除，发现数对R5C（4，6）={5，7}。

第四步：用数字9对第六列进行排除，因为数对R5C（4，6）={5，7}对空格R5C6的占位作用，得到R2C6=9。

至此，后续的工作均可以通过基础算法完成，不再赘述。

下面试着挑战一下后面的习题吧！

（摘自化学工业出版社《数独游戏：从基础到精通，让你越玩越聪明》）