基于Cov面截关联的线路几何变形综合因子预测模型研究

摘 要：针对线路施工过程发生几何变形的偶然性，建立单一因子模型数据可靠性差、精度低，因此本文提出考虑综合因子影响线路几何变形的Cov面截关联预测。该模型主要是通过建立综合综合因子变化模型的不确定参数以及采用大量数据的统计特性，来弥补模型中方差的不足，并考虑横截面数据存在的共性和差异特点，建立Cov面截关联，对比分析预测与实测数据，其结果验证了该方法在线路几何变形应用中的可行性，表明该方法能有效提高数据的可靠性和精度。

关键词：综合因子变化；Cov面截关联；预测分析

中图分类号：U 21 " " " " 文献标志码：A

线路顶进箱涵施工过程采用加固线路方式，开挖一段路基后顶进一段方式交替进行，会使原有应力状态遭受破坏，对线路运营产生影响。线路几何变形监测一直是保障线路安全运营的重要手段。新兴且成熟的监测方式越来越多地应用到线路外业监测，这些方法已经成为便捷采集线路几何变形数据重要手段之一。同时，线路几何变形监测数据也由较为成熟的单测点的数学模型等向多测点模型的不同量化因子的混合模型理论等方法扩展，例如众多研究采用灰色理论、混沌模型、人工智能、统计学习理论等多种模型组合的方式，对线路几何变形规律进行分析、预测，取得良好的效果。虽然这种分析方法已经非常成熟且实用，但是却忽略了监测点之间的关联性，无法从整体把握线路几何变形规律。本文建立监测点数据联系，对影响因子进行逐一及综合分析，从多尺度等角度分析线路的位移规律，为分析线路复杂的变形规律提供众多思路。从多因素角度分析特点，利用支持向量机分类的优势[1]，分析线路中长期的监测资料，充分考虑监测点的位置信息，对线路几何变形监测数据进行计算分析。

1 数学建模原理

1.1 常规统计模型

1.1.1 常规建模方法

根据成因，可将线路几何变形分为线路道床充盈分量δH、路基土压力分量δT两个部分，变形的计算过程如公式（1）所示。

δ=δH+δT " " " nbsp; " " " " "（1）

基于工程力学原理，在线路施工作业过程中，线路水平轨距与竖向轨距受到水平力与垂直力作用，因此该模型的表达式如公式（2）所示。

（2）

式中：Hu、Hu0为对应往后观测、初始观测所得到的数据；t为对应观测日至初始观测时间；t0为第一次观测到初始观测的时间；θ=t/100，θ0=t0/100；其他为回归系数。

1.1.2 模型参数求解

基于回归理论，传统模型可用公式（3）～公式（7）表示。

（3）

（4）

（5）

（6）

（7）

式中：Y为观测值；β为待估参数；X为对应自变量；ε为随机误差。

为了求解参数β，进行最小二乘平差求取结果，得到公式（8）。

=（XTX）-1XTY " " " " " " " "（8）

1.2 Cov面截关联模型

Cov面截关联模型既要保持共性，又要体现其差异，其表达式如公式（9）～公式（12）所示。

Y=Xβ+μ " " " " " " " " " " （9）

（10）

（11）

（12）

式中：μi包括垂直线路方向截面 i和关于时间t的回归常数与随机误差。其与传统模型区别是此处的Y是二维的，即除了在时序上的观测数据变化，还包括空间垂直线路方向截面上观测数据变化[2]。

X仍为自变量结构矩阵，但此时自变量结构矩阵的第一列元素不再为“1”，因此由自变量结构矩阵决定的回归参数中不含常数项，结合线路变形特点，可知X可由道床充盈度和路基土压力两种影响因子组成[3]。

2 实例分析

2.1 工程概况

本文所用数据来源于宿州市某省道穿越符离集站立交工程项目。本工程位于符离集站北场内，路基区域为直线段落，本工程为顶进箱涵穿越既有线9股道，预留线3股道。新建四孔（9+9+9+9）m分离式框构，由东向西下穿符离集站既有9股道，箱身全长58.4m。本工程属于国铁I级铁路，电气化铁路，钢筋混泥土枕，有砟轨道，设计目标速度160km/h。

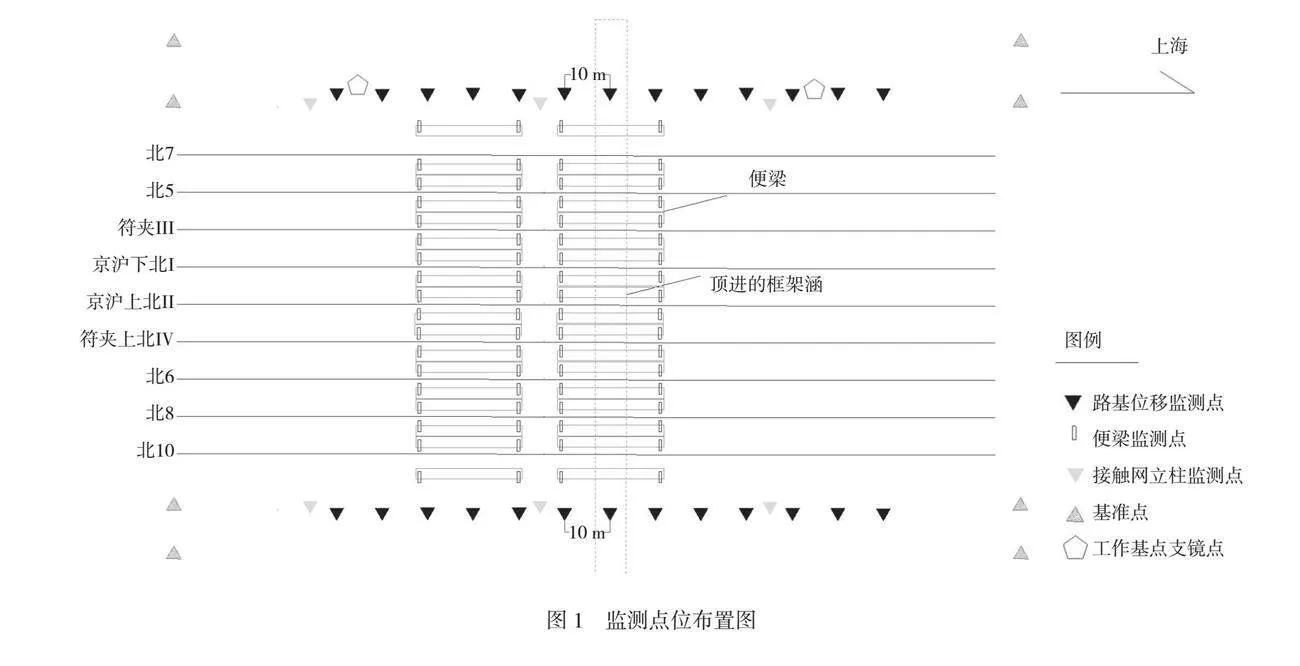
箱涵顶进前已完成基准点、工作基点、便梁监测点、路基监测点、电气化接触网立柱监测点等布设工作，具体监测点位布置如图1所示。

2.2 数据预处理

考虑Cov面截数据模型的具体效应量代表单个测量点偏离整个面板效应的幅度“公差”，因此选择了路基、便梁和同一横截面轨道垂直位移的Cov面截数据，建立对应的模型并研究线路的垂直位移变形。此外，由于受架空接触网搬迁的影响，面板中的所有测量点都需要考虑最后一个测量点获得稳定初始值所需的时间，并避免由于“单位根”和协整问题导致的面板数据虚假回归，建模时间间隔为2021年5月25日—2021年8月30日。

2.3 本工程Cov面截数据模型分类及检验

本工程采用变截Cov面板数据模型的表达式如公式（13）、公式（14）所示。

Y=Dα+Xβ+ε " " " " " " " "（13）

（14）

D的表达式如公式（15）所示。

（15）

该随机效应模型假设αi与εi是与自变量矩阵X不相关的随机变量，将这些变量组合的模型称为误差随机模型，并需要对上述建立的模型进行假设检验，原理：先建立原假设E（αi|Xi）=0，当具备这些条件时，再使用FGLS方法获得估计回归系数βFGLS（该回归系数差异不应显著），其特征随着样本增加而减少，逐渐接近0。构造统计量W，如公式（16）所示。

W=（βLSDV-βFGLS）Ω1-1（βLSDV-βFGLS） " " "（16）

式中：Ω1-1为协方差矩阵。

当原假设成立时，该模型符合自由度为K的χ2分布。应用F检验法对上述模型统计量进行假设检验，即用统计量F进行检验，如公式（17）所示。

（17）

式中： S0、S1分别为传统模型、 Cov面截关联模型的残差平方和；T为观测周期。

2.4 模型检验

模型检验结果见表1～表3。

通过F测试可以看出模型1和模型2构建的混合模型的决定系数R2分别为0.78、0.81，表明拟合优度相对较差（应将其排除在外），根据表3统计的结果，基于R2的判断系数标准，Cov面截关联数据Model拟合优度均大于0.9，且标准偏差分别只有2.77mm和3.01mm，其精度明显有所提高，因此优先选择Cov面截距数据模型。

2.5 建模成果及外延性评价

便梁道床充盈度模型预测与实测累计变化量如图2所示。

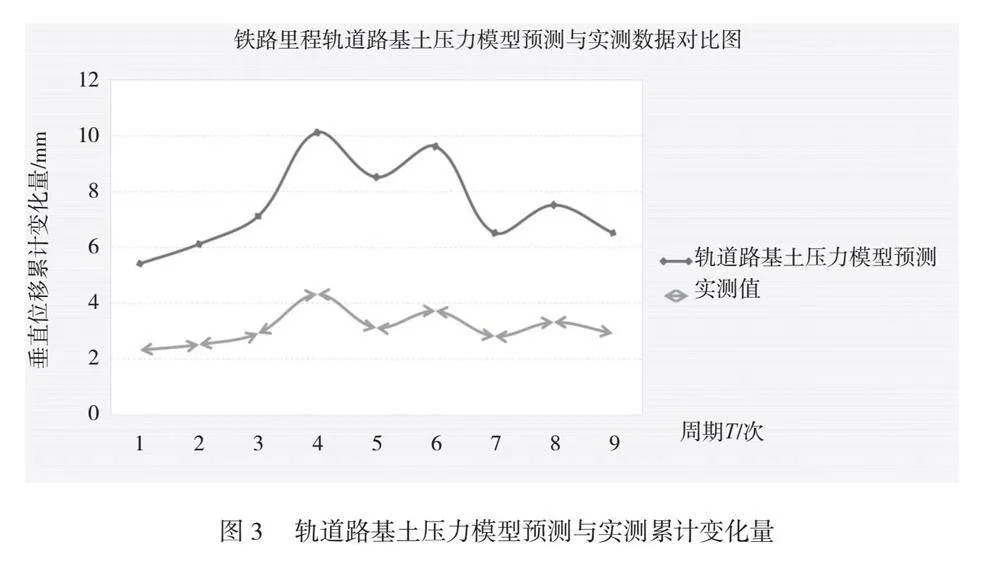
轨道路基土压力模型预测与实测累计变化量如图3所示。

Cov面截综合因子模型预测与实测累计变化量如图4所示。

通过建立单一因子模型，由图2得知，道床充盈度模型预测与实测最大误差为2.1mm，由图3得知，路基土压力模型预测与实测最大误差为6mm，其单一模型与实测值变化误差均较大，超出可允许误差2mm。由图4得知，考虑综合因子（道床充盈度和路基土压力）后，Cov面截综合因子模型预测的垂直位移与实测数据显示一致，基本保持平坦，建立的Cov面截关联模型与实测值最大误差在0.4mm，其精度能满足相应规范要求，说明Cov面截关联数据模型较好地克服了预测数据发散行为，具有良好的收敛一致性。

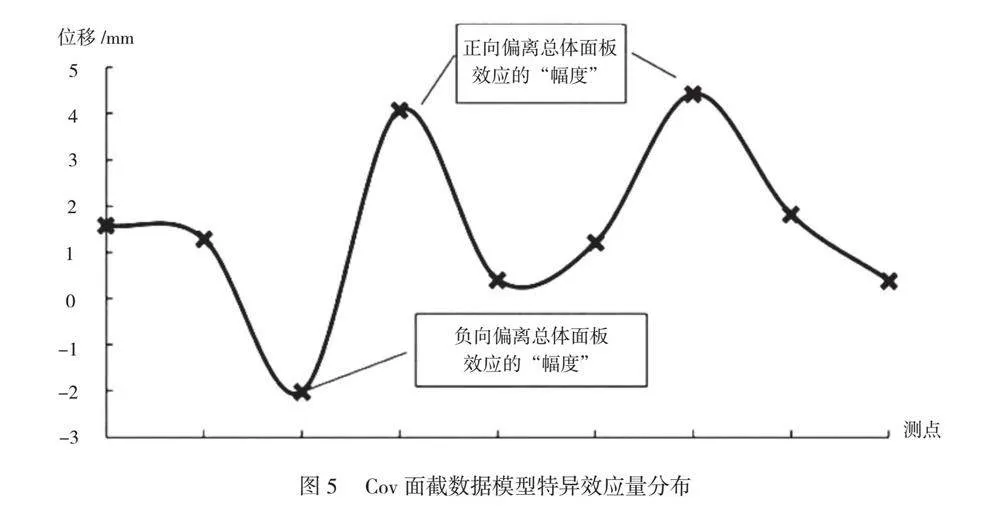
Cov面截数据模型特异效应量分布如图5所示。

通过研究模型中每个测量点的具体影响量αi分布，由图5得知，Cov面截数据αi的正、负及幅度表示面板中测量点偏离整体面板效应的方向及幅度保持在2～4mm，符合测量精度要求，说明Cov面截关联模型具有良好的可扩展性，在超过一个周期的预测区间内，模型中的测量点可以准确地感知影响因素变化引起的变形响应。因此，它不仅可以定义面板面积的“公差”，还可以将整条线建模为块。

3 结语

本文针对线路沉降因素较多，单因子数据模型已无法满足预测精度的问题，提出分别建立单一因子、综合因子的影响线路几何变形的Cov面截关联预测，建立模型与监测数据进行预测和对比分析，得到以下结论。1）对比单一因子模型与综合因子模型预测与实测累计变化量，得出其线路沉降受道床充盈度和路基土压力两者共同作用，建立的综合因子Cov面截关联模型与实测数据保持相对稳定的状态，可以为当前线路变形数据提供可靠支撑。2） Cov面截关联数据模型的特异效应量αi的正负与大小分别表征个体测点偏离总体面板效应的方向与幅度。因此可将特异效应量作“限差”识别线路测点的面板属性，并分块建模，其拟合精度及外延性证明，采用Cov面截关联数据模型对线路进行分块建模是可行的，且该模型具有较好的预测能力，也可对线路进行在线实时监控、分级预警。3）本文采用Cov面截关联数据对长序列大样本的监测数据进行建模，统计数据表明，该模型具有控制异质性的特点，且参数能兼顾整个面板区域测点的变形特性，也可弥补常规统计模型仅针对单一测点评价变形分量的局限性，并且还可减少因子的多重共线性、鲁棒性等，具有较好的探索研究价值和应用前景。

参考文献

[1]侯涛.基于沉降特性的沉降预测方法[J].测绘技术装备，2022，24（4）：11-14.

[2]李红祥， 岳东杰， 李立瑞. 基于主成分回归的大坝位移模型[J]. 水电自动化与大坝监测，2008，32（5）：61-64.

[3]王继敏，顾冲时，张晨，等.基于面板时空模型的锦屏一级大坝变形性态分析[J].水力发电学报，2020，39（11）：21-30.

通信作者：黄明翔（1990—），男，江西上饶人，工程师，研究方向为精密工程测量、空间数据处理与质量控制。

电子邮箱：minson.huang@qq.com。