架空输电线路无跨越架封网计算方法研究

摘 要：首先，本文在封网参数的基础上对封网承力索张力进行计算，并分析承力索最初的设置阶段、正常工作阶段以及承力索存在故障阶段的张力。其次，确定封网状态下承力索弧垂，计算交叉跨越净空距离。最后，结果表明，算法2中空载状态下承力索张力为4279.66N，安全系数仍为50，与施工方案规格的匹配度更理想。经本文方法计算的承力索空载拉力值、承力索封网后拉力值、空载时承力索弧垂、封网后承力索弧垂值与测量结果相差的数值分别为26N、24N、0.075m、0.006m，最大误差率不超过0.42%。由此可见，本文提出的计算方法更适合运用在实际架空输电线路建设施工中。

关键词：架空输电线路；无跨越架封网；承力索张力；承力索弧垂；安全系数

中图分类号：TL 098 " 文献标志码：A

随着国民经济快速发展，电网建设也在与时俱进，输电线路建设作为电网建设的重要内容，其建设过程中经常会出现跨电力线的问题。由于工程现场的施工需求，无法对被跨越的电力线停电，因此要求在跨越电力线过程中不可以无电跨越[1]。随着输电线路建设方案优化，以迪尼玛绳索作为承力索，该绳索不仅绝缘且张力更佳，绝缘网的安装离不开承力索的支撑[2]。在安装导线的过程中发生故障导致导线突然掉落，绝缘网会接住导线，不会因导线直接掉落在其他电源线路而造成更大的事故，输电线路施工过程需要保持带电状态。迪尼玛绳索规格型号的选择决定承力索的张力以及后续故障状态时绝缘网的承接力，因此需要选择符合施工要求的迪尼玛绳索[3]。本文采用在塔上悬挂临时横担，在临时横担上悬挂滑车，在滑车里设置承力索，在承力索上封网保护高压电力线的施工方法，该方法更简单，安全风险也相对较小。但使用这种方法进行跨越封网需要合理选择迪尼玛承力索的规格，承力索的受力计算就显得尤为重要，为架空输电线路不停电跨越施工提供技术支持。

1 无跨越架封网计算

1.1 封网参数确定

表1为不同轴承在220kV电压下的红线Ⅰ和Ⅱ的参数情况，并结合工程中实际的跨越状态，对220kV电压下的红线进行不停电封网，此时在工程线路的三相导线的部位设置单相封网成为主要的封网方法，而其具体的宽度C和单位长度的风压W4（10）满足的相关计算如公式（1）所示。

C≥2W4（10）[m（l-m）/（2H）+λ/ω]+b，W4（10）=0.0613kd

（1）

式中：m、l、H分别为现场线路附近的杆塔与跨越架之间的横向长度、跨越档之间的长度、导线水平张力；λ、ω、b、k、d分别为现场线路放线滑车的总长、定量导线质量、面相横向的同相子导线之间的长度、空气动力系数、导线直径，这里的空气动力系数为1.1[4]。

此时，保护下面线路的绝缘网长度lW须满足lW≥n/sinα+C/tanα+2lb[2]，其中n、α、lb分别为被跨越的红线其两端线路之间的长度、跨越过程中产生的角度、绝缘网的一端超过电力线的距离。一般会选择一种绝缘杆作为封网工具，该工具通常为玻璃钢材质，长度为6.5m，绝缘杆数量为12根，间距固定为3.5m，且绝缘杆间通过长度为3.5m的绳子连接控制，并将绝缘杆横吊在2条垂直向下的迪尼玛绳子上，2条绳子（型号为ø18）间的距离为6.5m，绝缘杆的横吊工具通常为滑车或者环扣[5-6]。

要搭建一个临时的横担，通常选择钢制的横担，尺寸为32.5m×0.55m×0.55m，铁塔本身有一个横担，因此临时的横担通常设置在原横担的下方，并距离原横担8.5m。

1.2 封网承力索张力计算

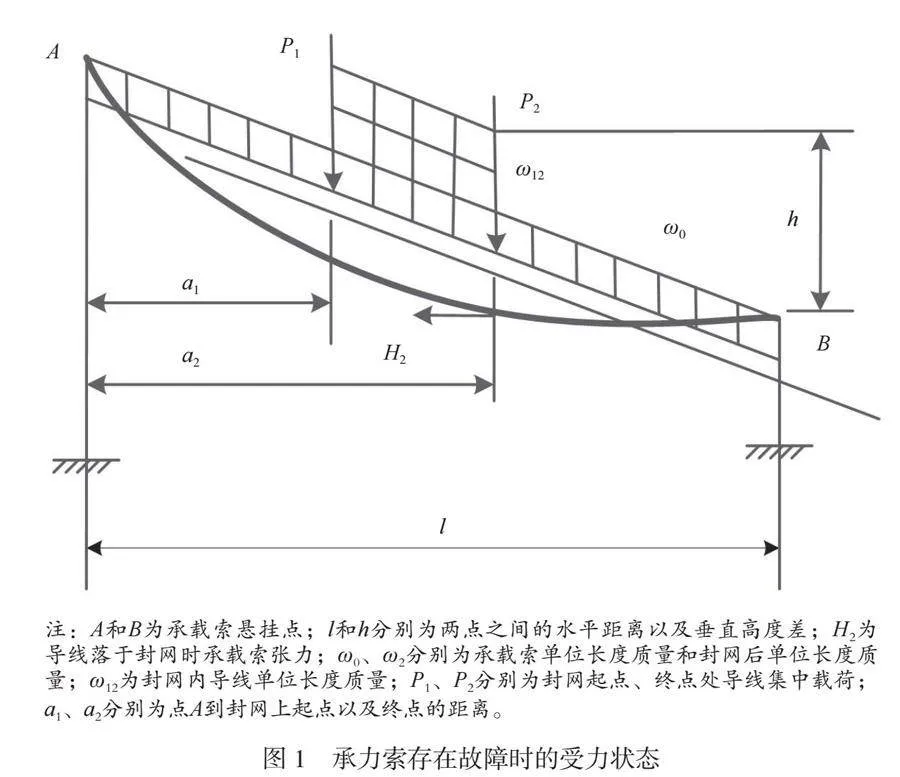
承力索的状态分为2种，一种是正常的工作状态，另外一种是存在故障时的工作状态[7]。当正常工作时，承力索承受自身质量和封网设备质量2个方面的力，此时的荷载分布均匀，且只有1个荷载。但当承力索存在故障时，导线会从高处落下，掉落至保护网中，此时承力索除了承受自身封网设备的质量外，还要承受落入保护网中导线的质量，此时荷载分布均匀，但封网的两侧均要承受一个荷载，均匀分布的荷载以及聚集在一处的荷载，单根承力索承受质量按封网后质量叠加的一半计算，同时导线分裂成多个单位长度和单位质量的导线，承力索存在故障时受力如图1所示。封网承力索张力要根据承力索所处的阶段来计算，承力索一般处于3种阶段，最初的设置状态阶段、正常工作阶段、承力索存在故障时的阶段。因此，要根据不同阶段分别对承力索的张力进行计算[8]。

上文获取了承力索在最初的设置状态阶段的张力，需要通过承力索状态公式获取封网状态下的承力索张力H1，如公式（2）所示。

（2）

式中：K0为第一阶段承力索张力；l为跨越档之间的长度；ω0为承载索单位长度质量；S为承力索截面积；E为承力索弹性模量；K1为封网状态下的承力索张力；h为承载索悬挂点之间垂直高度差。

其中，满足ωt=ω0+ωf（ω1、K1、β分别为封网状态下的承力索单位长度质量、对承力索加长的系数以及跨越档长度差距，跨越档长度差距满足tanβ=h/l）。

如果封网位置与跨越档位置出现交集时，跨越档长度差距满足K1=K12-K11，此时跨越档内部封网的起点和终点的长度差距如公式（3）所示。

（3）

式中：ω0为承载索单位长度质量；ω1为封网状态下的承力索单位长度质量；ai为承力索上的力点与封网之间的直线距离，且满足i=1或2，此时 i表示封网的始末点。

当承力索处于故障时，分为静态和动态2个阶段。当处于故障的静态阶段时，导线落入封网内，承力索张力增加，此时承力索张力为H2，如公式（4）所示。

（4）

式中：K3为导线掉落封网内因重力而造成封网长度增加的系数；K4为导线掉落在封网内，因封网两侧的荷载增加而导致承力索长度增加的系数。

同时K3=K32-K31，ω2=ω1+ωd。此时跨越档内部封网的起点和终点的长度差距如公式（5）所示。

（5）

式中：ω2为封网设备质量和导线单位质量的总和；ωd为封网过程中导线单位质量，且K4=K42+K41。

此时跨越档内部封网的起点和终点的长度差距如公式（6）所示。

（6）

式中：Pi为封网两侧的荷载。

同时满足，。

当处于故障的动态阶段时，导线落入封网内，承力索张力增加，此时承力索张力为H3，而承力索单位长度质量满足 ω3=ω1+KdKhωd，且导线从高处掉落至封网中，因为自身重力造成一瞬间的冲力，该冲力系数用Kd 表示，在单回路时冲力系数为1.56，双回路时冲力系数为2.78。Kh表示导线掉落后的不均衡系数，该系数为1.16。承力索故障时其动态安全系数满足Ks=Tp/K3，且Ksgt;6。

1.3 封网状态下承力索弧垂

当承力索存在故障时，跨越物上方的封网最低点与被跨越物之间的垂直距离需要满足安全规则的要求，计算跨越点封网最低处的弧垂，如公式（7）所示。

fx=hA+x×tgβ-s-hx （7）

式中：s、x、hx、hA、β分别为故障时封网凹点与被跨越物之间的长度、被跨越物上方封网的最凹点与杆塔之间的距离、被跨越物最高点的高程、塔杆A点的承力索高程、AB两点的承力索跨越过程中产生的角度。

1.4 交叉跨越净空距离计算方法

结合上文获取的封网承力索张力相关计算，根据电线力学理论及几何关系可以推导出相关公式。

在导线的布置过程中，导线上任何一个点的弧垂如公式（8）所示。

（8）

式中：Wd、Td分别为子导线质量以及子导线的张力，通常会选择12%的破断张力。

导线点的高程如公式（9）所示。

（9）

封网承力索点的高程如公式（10）所示。

（10）

导线设置时，与封网承力索间的净空距离如公式（11）所示。

Δh=hDx-hx （11）

封网承力索距所跨线路的净空距离如公式（12）所示。

Δh=hx-h0，x=l0 （12）

获取承力索空载、正常运行、静态故障、动态故障4种情况下净空距离。当交叉跨越净空距离不符合要求时，需要对封网装置点高程、初始安全系数等进行调整。

2 架空输电线路计算方法验证

2.1 承力索张力对比

以某地区电力设计有限公司所承包的工程项目为例，该项目中存在110处封网跨越区域，均为不停电操作，通过本文方法在不停电的情况下完成项目设计及布置。该项目整体电压为220kV，将线路设计成同塔双回路，选择钢芯铝材质的导线，该导线型号通常为2×JL/G1A-630/45，试验中需要进行不停电施工。采用3种算法对该项目的相关数据进行计算。

算法1：将各工况下单根承力索受力视作均布荷载，各工况下单根承力索单位质量以档距为折算距离。

算法2：均匀分布的荷载以及聚集于一处的荷载，单根承力索承受质量按封网后质量叠加的一半计算，同时导线分裂成多个单位长度和单位质量的导线，算法2为本文采用的计算方法。

算法3：故障发生前的承力索受力看成一个均匀分布的荷载，故障发生时看成2种均匀分布的荷载和聚集于两侧的荷载，封网后单位质量通过绝缘绳长度获取。

通过3种算法计算承力索张力，见表2。算法1与算法2计算出的承力索张力数据更接近，算法3因数据不符被排除。对比算法1和算法2可知，算法1中，空载状态下承力索张力为2492.39N，安全系数为50。而算法2中空载状态下承力索张力为4279.66N，安全系数仍为50。因此算法2中的承力索张力值及安全系数与其规格的匹配度更理想，本文计算方法更适合运用在实际的输电线路建设中。

2.2 计算结果与实测数据对比

通过本文算法计算承力索空载拉力、空载时承力索弧垂、承力索封网后拉力、封网后承力索弧垂，同时通过仪器实测各个数据，2种数据如图2所示。现场测量的承力索空载拉力值为6462N，本文计算值为6436N，错误率0.4%；现场测量的承力索封网后拉力值为8175N，本文计算值为8199N，错误率只有0.29%；现场测量的空载时承力索弧垂值为1.785m，本文计算值为1.71m，错误率0.42%；现场测量的封网后承力索弧垂值为2.854m，本文计算值为2.86m，错误率0.21%；由此可见，通过本文研究的计算方法计算出的相关数据与实际测量数据很接近，且错误率最大不超过0.42%，因此本文研究的计算方法所计算出的数据准确率极高。

3 结语

在本文对架空输电线路无跨越架封网算法的研究中，进行了封网承力索张力、封网状态下承力索弧垂、交叉跨越净空距离的计算。因为封网承力索张力的计算过程中，施工状态存在多样性，所以对不同阶段的承力索张力进行计算。试验结果表明，与其他算法相比，本文计算空载状态下承力索张力为4279.66N，安全系数为50，与工程方案要求的规格匹配度更理想；现场测量的承力索空载拉力值、承力索封网后拉力值、空载时承力索弧垂值、封网后承力索弧垂值分别为6462N、8175N、1.78m、2.85m，而本文算法得出值分别为6436N、8199N、1.71m、2.86m，计算值错误率最大不超过0.42%，因此本文研究的计算方法所计算出的数据准确率极高，且更适合运用在实际的输电线路建设施工方案中。

参考文献

[1]陈亦，曾远，李晓斌，等.超高分子聚乙烯绳索在封网跨越施工中的应用[J].机械设计与制造，2023（4）：152-157.

[2]夏拥军，贾宁，万建成，等.悬索式跨越架用纤维绳索非线性本构关系试验研究[J].机械设计与制造，2021（2）：58-61.

[3]孟凡豪，夏拥军，马勇，等.悬索式跨越架用吸能装置吸能效果试验分析[J].振动与冲击，2022，41（8）：11.

[4]黄力，唐嘉晖，唐波，等.基于特征模理论的输电线路铁塔无源干扰研究[J].高电压技术，2023，49（6）：2598-2606.

[5]吴田，付道睿，彭勇，等.1000kV输电线路耐张塔带电作业电位转移电流脉冲波形特征参数研究[J].电网技术，2022（46）：33-36.

[6]邹丹旦，余霜鸿，邵戎，等.考虑复杂山地风加速的架空线路风偏闪络故障分析[J].电瓷避雷器，2022（4）：9.

[7]杨刚，傅中，程洋，等.同塔双回输电线路相参数新测量计算方法[J].电网技术，2023，47（6）：2522-2529.

[8]周伟绩，李凤婷，解超，等.基于准两相跳闸的同杆双回输电线路跨线故障跳闸策略[J].南方电网技术，2023，17（11）：130-137.