建筑工程中岩土边坡抗剪强度勘察技术研究

摘 要：由于传统岩土边坡抗剪强度勘察技术直接对岩土边坡抗剪强度勘察模型进行构建，未对岩土边坡应力分布状况进行解析，造成传统方法勘测效果较差，因此本文提出建筑工程中岩土边坡抗剪强度勘察技术研究。对岩土边坡应力分布状况进行解析，结合施工地区现有的岩土边坡调研结果，构建岩土边坡抗剪强度勘察模型，设计抗剪强度勘察流程，并对岩土边坡抗剪强度勘察值进行输出，设计对比试验。试验结果表明，该研究方法的勘测结果更接近真实岩土边坡抗剪强度，勘测结果更准确。

关键词：建筑工程；岩土边坡；抗剪强度；勘察技术

中图分类号：TU 45 " " 文献标志码：A

岩土边坡抗剪强度在建筑工程中具有重要意义，它直接关系到土体的稳定性和工程的安全性。岩土边坡是指土体与岩石相交处形成的斜坡，其稳定性对道路、铁路、水利工程等基础设施的设计和施工，乃至整个社会的发展都起着至关重要的作用[1]。岩土边坡的各种灾害事件时有发生，如滑坡、崩塌、泥石流等，给人民群众的生命财产带来了严重的损失。因此，加强岩土边坡抗剪强度的研究具有紧迫的现实意义。本文旨在对岩土边坡抗剪强度勘察技术研究进行深入探讨，分析岩土边坡的特性和力学行为，以期为工程师和决策者提供科学、准确的参考信息。

1 建筑工程中岩土边坡抗剪强度勘察方法设计

1.1 岩土边坡应力分布状况解析

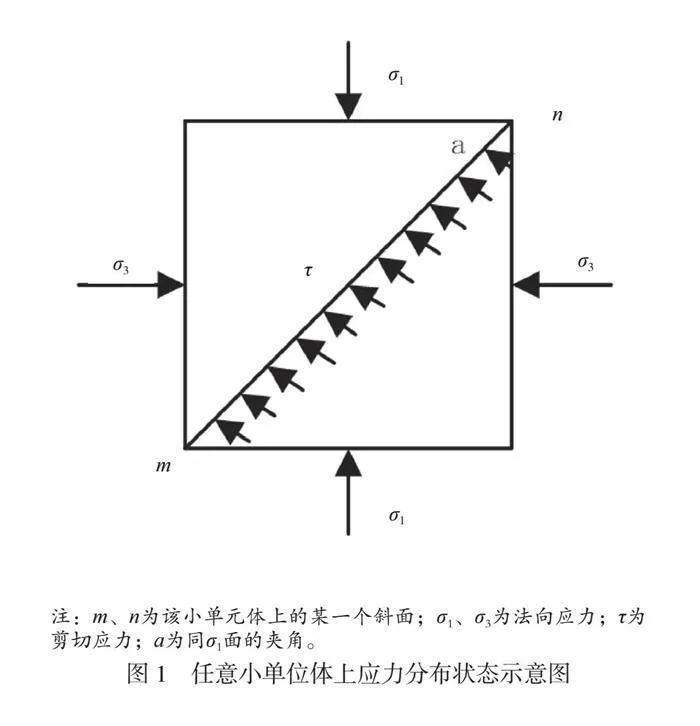
为了分析土壤应力分布情况，可以通过分析小的单位应力分布来解析岩土边坡应力分布状况[2]。对土体中任一点进行选择，设定该点为1个小单元体，如图1所示。

根据图1可知，此时小单元中的应力分布可由公式（1）、公式（2）表示。

τ=1/2（σ1-σ3）sin2a " " " " " " " " " "（1）

σ=1/2（σ1+σ3）+1/2（σ1-σ3）cos2a " " " " （2）

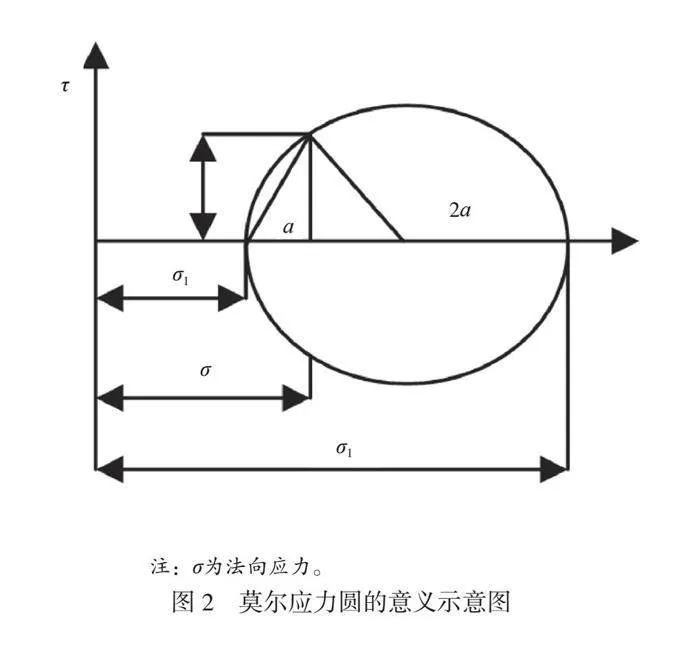
此外，如图2所示，莫尔应力圆可以直观地表示任意小单位体上应力分布状态。

通过图2可以看出，该图以点（1/2（σ1+σ3），0）为圆心，在σ-τ坐标系中，以1/2（σ1-σ3）为半径画圆。当小单元体或者土体中2a等于90°时，刚好处于剪应力最大值的形态，此时τmax=1/2（σ1-σ3）。如果要添加新变量，可以使用与默认变量相同的变量。

由于土体可以在不同的应力状态下达到破坏，因此可以绘制很多不用应力状态下的莫尔应力圆[3]。组成达到极限平衡状态时的曲线，绘出多个莫尔应力圆的公共切线（称为土体抗剪强度包线）。恰好满足极限平衡条件的土体抗剪强度包线正好切于莫尔应力圆圆周的点位。此时，通过达到边界平衡状态来全面描述应力分布，如公式（3）～公式（5）所示。

1/2（σ1-σ3）=Ccosφ+1/2（σ1+σ3）sinφ （3）

σ1=σ3tan2（45+φ/2）+2Ctan（45+φ/2） （4）

σ3=σ1tan2（45-φ/2）-2Ctan（45-φ/2） （5）

式中：C为莫尔应力圆圆周；φ为主应力施加方向与公共切线的角度。

如果土体中的小单位应力分布满足边界平衡条件，那么主应力施加的最大方向为90°。在剪应力破坏表面的方向与主应力作用的最小方向之间建立角度，如公式（6）所示。

acr=1/2（90°+φ）=45°+φ/2 " " " （6）

1.2 构建岩土边坡抗剪强度勘察模型

在岩土边坡应力分布状况解析后，可结合施工地区现有的岩土边坡调研结果，建立岩土边坡抗剪强度勘察模型。其中，抗剪强度后验概率分布与现场试验数据之间的关系如公式（7）所示。

（7）

式中：u为场地数据样本；μ和σ分别是未加工强度参数的平均值和标准差；f和S分别是偏离未加工强度参数分布的平均值和标准差。

将贝叶斯理论引入岩土工程参数的可变性并进行研究。其基本思想是整合传统未开发抗剪强度的经验范围和当地研究数据，并通过未开发的抗剪强度和变量经验公式来评估未开发的抗剪强度参数及其可变性。考虑开发的抗剪强度为服从对数正态分布的连续变量，引入贝叶斯的理论框架来求解抗剪强度变异性的过程。基于先前信息（即抗剪强度值的经验范围等）和液性指数来估算抗剪强度的概率分布参数，即均值和标准差。

该解决方案的思路是基于液性指数和抗剪强度的经验公式，确定由抗剪强度重新分配的可能密度函数的形式[4]，即P（LI，Prior），其中，LI为液性指数，Prior为对数值。根据先前关于该区域内抗剪强度的信息和液性指数测试指标，使用马尔可夫链蒙特卡罗的抽样方法，在先前概率密度函数的基础上产生与抗剪强度具有相同概率的等效样本。计算等效样本和贝叶斯分析的平均值和标准差。基于抗剪强度参数的先验信息和液性指数的现有现场调查数据，应用贝叶斯分析，抗剪强度的后部分布密度函数如公式（8）所示。

P（Su|μ，σ）=P（μ，σ|LI，Prior）dμdσ " " " "（8）

式中：P（μ，σ|LI，Prior）为抗剪强度Su平均值u和标准差σ的总体概率密度函数。

P（μ，σ|LI，Prior）可以结合贝叶斯公式计算先前信息数据，如公式（9）所示。

P（μ，σ|LI，Prior）=K·P（LI|μ，σ）P（μ，σ） （9）

式中：P（μ，σ）为先验分布；P（LI|μ，σ）为概率函数；K为归一化常数。

由此，利用密度函数重新分配抗剪强度产生的等效样本，不会影响分配的计算结果。抗剪强度的先前信息经过传播后，抗剪强度的平均值和标准偏差范围描述如公式（10）所示。

（10）

式中：μmax为平均抗剪强度的最大值；μmin为平均抗剪强度的最小值；σmax为抗剪强度标准差的最大值；σmin为抗剪强度标准偏差的最小值。

以可能性函数描述抗剪强度和液性指数之间的联系，计算过程如公式（11）所示。

LI=aln（Su）+b " " " " " " " " " " " " "（11）

其中，a=-0.452，b=2.336。

假设抗剪强度Su是一个连续变量，呈对数正态分布。设标准正态分布变量z为抗剪强度的对数值，进一步延展抗剪强度的分布变换如公式（12）、公式（13）所示。

ln（Su）=μN，Su+σN，Suz " （12）

（13）

假设液性指数偶然不相关，那么多组液性指数数据的独立多元正态概率密度函数如公式（14）所示。

（14）

式中：N为测量的液性指数值的个数。

岩土边坡抗剪强度勘察模型如公式（15）所示。

P（Su|LI，Prior）=K·∫P（Su|μ，σ）P（LI|μ，σ）P（μ，σ）dμdσ " " " " " " " " （15）

式中：K为多元正态分布的斜方差矩阵。

1.3 岩土边坡抗剪强度勘察值输出

直接求解抗剪强度的模型相关的概率密度函数较为困难。蒙特卡罗是一种采样解决方案。使用蒙特卡罗方法来求解上文设计的岩土边坡抗剪强度勘察模型，从一个目标分布中生成随机样本序列作为目标分布点，也称为对应于目标的上述散布点样本。使用上述构建模型，生成岩土边坡抗剪强度勘察值，详细情况如下。

首先，对马尔科夫状态链进行初始化，令Su，0=（μmax+μmin）/2最终结果不受初始状态影响。

其次，设u=1重复以下步骤，假设Su，0为u=0时刻状态的抗剪强度；进行抽样，随机得到下一个状态Su，i；随机生成一个均匀分布的随机数u，如果，

那么接受转移，此时Su，i相等，再进行迭代计算。

最后，在贝叶斯分析的背景下，结合液性指数作为观测值，样本的等效平均值和标准差被用作“等效”变量。基于上述建立模型，以等效样本的均值和标准差作为抗剪强度“等效的”变异性，输出岩土边坡抗剪强度勘察值。抗剪强度勘察流程如图3所示。

抗剪强度勘察值计算流程如下。1） 从岩土边坡土体测试中获得液性指标值。2） 获得该地区范围内抗剪强度参数值，包括平均值和标准差范围。3） 计算模型中似然函数的后验分布概率密度函数，考虑先验信息和概率函数。4） 计算马尔可夫链的初始位置。5） 计算等效样本的平均值和标准差，即等效的抗剪强度均值和标准化，使用30000当量的抗剪强度等效样本取均值，输出岩土边坡抗剪强度勘察数据。

2 试验论证

2.1 试验准备

以本建设项目为例，在实际施工过程中，具体包括3个岩土工程边坡抗剪强度勘测，即2个一级边坡和1个三级边坡。此外，还有一些基坑周边为土质边坡，集中在周围地区。石质和土质的最高高度为39m，属于斜坡类型。此外，勘探区两侧还有一些开挖方边坡，均为高度4m～8m的石头和土壤边坡。为了保证工程的顺利进行，对岩土边坡抗剪强度进行勘测研究。根据以往的施工经验，岩土边坡表面的垂直强度可能会影响边坡下滑力。确定岩土边坡抗剪强度是保证其稳定性的重要依据。该项目使用地质计算软件和Bishop切片法来探索施工边坡地质的稳定性。岩土物理力学指标参数见表1。

边坡稳定性计算结果分析见表2。

2.2 对比试验

对表1和表2的数据结果进行分析可知，该项目存在重大安全风险，必须进行充分的支护工作，以避免出现边坡不稳定的问题。本文对岩土边坡的纵向抗剪强度进行勘测。在岩土边坡下方2cm和8cm处采集了6个圆刀形样本，用于垂直荷载勘测，使用传统方法一、传统方法二和本文提出的方法分别对其进行纵向抗剪强度勘测，利用函数对不同方法勘测结果进行拟合计算，并将计算结果进行输出，3种方法试验结果对比见表3。

从表3中可以看出，本文提出的建筑工程中岩土边坡抗剪强度勘察技术与实际结果之间具有较高的拟合度。试验结果表明，本文提出的方法最大拟合和最小拟合值均在0.986以上，远远高于传统方法一和传统方法二的拟合度（0.903和0.918），表明本文提出的方法的勘测结果更接近真实岩土边坡抗剪强度，勘测结果更准确，结果更可靠。

3 结语

本文的研究对于深入探讨建筑工程中岩土边坡抗剪强度勘察技术具有重要的理论意义和实践价值，本文构建1个全面的岩土边坡抗剪强度勘察模型并对模型进行计算和分析，获取准确的岩土边坡抗剪强度勘察值。将勘察结果与工程实际相结合，提出相应的建议和措施，为建筑工程的安全稳定提供有力支持，可以为相关领域的工作提供参考。同时，还可以为保障建筑工程的安全性。

参考文献

[1]顾春生，唐鑫，朱常坤，等.基于主成分分析法优化神经网络的滆湖组黏性土抗剪强度预测[J].科学技术与工程，2023，23（28）：11980-11989.

[2]范亚坤，郑明新，吴珺华，等.干湿循环下煤系土抗剪强度与微观结构参数关联度研究[J].南昌航空大学学报（自然科学版），2023，37（2）：52-62.

[3]刘建平，周花玉，何天奎，等.含根量对根–土石复合体的抗剪强度影响试验初探——以垂丝海棠为例[J].岩石力学与工程学报，2023，42（增刊1）：3618-3628.

[4]张泽，白子玉，贺玉莹，等.基于流变学方法的沥青中高温性能及胶浆抗剪强度研究[J].河北工程大学学报（自然科学版），2022，39（4）：56-61，85.