风电经构网型柔直送出系统小扰动稳定性分析

摘 要：柔性直流输电（VSC-HVDC）技术已成为海上风电并网的主流趋势。目前，VSC-HVDC主要采用跟网型控制，但跟网型控制的系统容易出现小扰动稳定性问题。针对该问题，本文在柔性直流输电系统的整流侧采用构网型VSG（虚拟同步发电机）控制，建立了海上风电场经构网型VSC-HVDC送出系统的小扰动数学模型。利用特征值法分析了VSG控制参数对系统稳定性的影响。最后通过跟网型与构网型控制对根轨迹的影响分析结果的正确性。

关键词：VSC-HVDC；海上风电场；VSG；小扰动动态模型；特征值法；小扰动稳定性分析

中图分类号：TM 46 " " " " " 文献标志码：A

由于各种资源限制，中国的风电等新能源与电力需求呈反向分布。随着输电距离增加，鉴于交流电缆的无功充电效应，交流输电技术的经济优势逐渐减弱[1]。柔性直流输电（VSC-HVDC）具有潮流逆转快、事故后恢复供电和黑启动快以及无换相故障等优点，是风电长距离输电的最佳选择[2]。由于新能源并网和常规同步发电机安装比例降低，因此电网惯性低、阻尼不足。虚拟同步机（VSG）控制是一种常见的构网型控制。发生暂态故障或扰动时，VSG控制技术可提供惯性，从而提高电网的稳定性[3]。目前，将VSG控制技术应用于海上风电场经柔直送出系统的研究还很有限。

本文建立了风电场和柔性直流输电系统的小扰动模型，并分析其稳定性。其中，同步发电机和机侧变流器等效为恒流源，柔性直流输电系统等效为单端VSC模型。本文通过特征值分析，探究了惯性系数和下垂系数对系统稳定性的影响，并通过比较稳态和失稳参数验证了小扰动模型和特征值分析结果的正确性。

1 海上风电场经构网型VSC-HVDC送出系统

并网逆变器通过滤波电路、并网线路和升压变压器与VSC-HVDC系统相连，如图1所示。图1将聚合型风电场（SWF）简化为单个并网逆变器，由一台风力涡轮机和2台背靠背逆变器聚合而成。由于整流站和逆变站通过直流线路解耦，因此逆变站对整流站的影响可以忽略不计[4]，可将柔直系统的逆变侧等效为一个恒定直流源。

2 海上风电场经构网型VSC-HVDC送出系统的动态模型

2.1 风电场SWF动态模型

2.1.1 SWF交流线路的动态方程

风电场的有功功率在并网前需要经过滤波电路对高频谐波进行滤波。进而有功功率通过交流线路到达PCC点[5]。滤波电路和并网线路的动态方程如公式（1）～公式（3）所示。

（1）

（2）

（3）

式中：Vld、Vlq和ild、ilq分别为滤波线路的d、q轴电压、电流；Vod、Voq分别为变流器出口处的d、q轴电压、电流；Vsd、Vsq和isd、isq分别为集电线路的d、q轴电压、电流。

SWF控制系统包括6个一阶惯性环节，以响应控制器对交流电压或电流扰动的测量，如公式（4）所示。

（4）

式中：ildm和ilqm分别为滤波线路的d、q轴延时电流；Vodm和Voqm分别为变流器出口处的d、q轴延时电压；isdm和ilqm分别为集电线路的d、q轴延时电流；Tmid和Tmud为延时系数。

2.1.2 SWF控制回路的动态方程

SWF逆变器的控制目标是实现直流母线电压稳定，同时控制有功功率和无功功率，并通过采样SWF逆变器出口处的电压来实现有功电流和无功电流的解耦[6]，如公式（5）所示。

（5）

式中：e1～e5均为线性化的中间状态变量；Vdcref为直流电压的参考值；Q为无功功率；Qref为无功功率的参考值；Vref为功率环电压的参考值；Vm为相电压；Vn为额定电压；kivar为功率环积分系数；kpvdc和kivdc分别为并网逆变器d轴外环的比例系数和积分系数；kiv为并网逆变器q轴外环的积分系数；ildref和ilqref分别为并网逆变器出口d轴和q轴电流的参考值；ildm和ilqm分别为滤波电路的d轴和q轴的延时电流。

2.1.3 直流线路的动态方程

直流线路的动态方程如公式（6）所示。

（6）

2.1.4 锁相环的动态方程

PLL的动态方程如公式（7）所示。

（7）

式中：kpPLL和kiPLL分别为PLL的比例系数和积分系数。

2.2 VSC-HVDC系统的动态模型

2.2.1 整流侧交流线路的动态方程

VSC-HVDC交流系统动态数学模型如公式（8）、公式（9）所示。

（8）

（9）

式中：Vld1、Vlq1和ild1、ilq1分别为送端交流系统滤波线路的d、q轴电压和电流；Vod1和Voq1分别为变流器出口处的d、q轴电压；isd1和isq1分别为送端交流系统集电线路的d、q轴电流。

为避免代数回路，本文在VSC控制系统中加入了4个一阶惯性环节，以响应控制器对交流电压或电流扰动的测量，如公式（10）所示。

（10）

式中：ild1m和ilq1m分别为送端交流系统滤波线路的d、q轴延时电流；Vod1m和Voq1m分别为送端交流系统变流器出口处的d、q轴延时电压；ild1m和ilq1m分别为送端交流系统集电线路的d、q轴延时电流；

2.2.2 整流侧功率环的动态方程

VSG控制技术通过模拟同步发电机转子的运动方程，进行同步发电机的一次调频和电压励磁调节，控制方程如公式（11）所示。

（11）

式中：J为虚拟转动惯量，在机械方程中模拟发电机的惯量支撑电网；θ1为VSC-HVDC系统的相位角；ω0为额定角频率；ω1为VSG输出电压角频率；ωn为电网同步角频率；P为虚拟同步机控制输出电磁功率；Dp为阻尼系数；Vod1ref为送端交流系统滤波线路电压d轴的参考值；P1ref和Q1ref分别为虚拟同步机控制输出有功功率和无功功率的参考值；Vn为额定电压。

2.2.3 整流侧控制回路的动态方程

VSC-HVDC整流器控制系统的动态数学模型如公式（12）～公式（14）所示。

（12）

（13）

（14）

式中：e5～e8为线性化的中间状态变量；Vod1ref和Voq1ref分别为送端交流系统滤波线路电压d、q轴的参考值；ild1ref和ilq1ref分别为送端交流系统滤波线路电流d、q轴的参考值；kpv1、kiv1和kpi1、kii1分别为控制系统外环和内环PI控制器的比例系数和积分系数。

2.3 全系统小扰动模型

由于风电场和VSC-HVDC系统基于不同的旋转坐标系，因此需要对2个系统间的相位角进行转换，如公式（15）所示[7]。

（15）

式中：iod和ioq分别为风电场逆变器出口处的d、q轴电流；θ为风电场系统的相位角。

根据上述子系统的小扰动模型，可得海上风电场经VSC-HVDC并网的整个系统的小扰动模型，如公式（16）所示。

（16）

式中：Δx为线性化状态变量，由上述动态方程线性化后可得；Δu为线性化输入变量；A为状态矩阵；B为输入矩阵。

3 小扰动稳定性分析

特征值分析是分析小扰动稳定性的常用方法。通过分析参与因子，可得特征根对应的模态与状态变量间的相关性，从而进一步分析系统扰动发生的原因[8]。

3.1 惯性系数J对根轨迹的影响

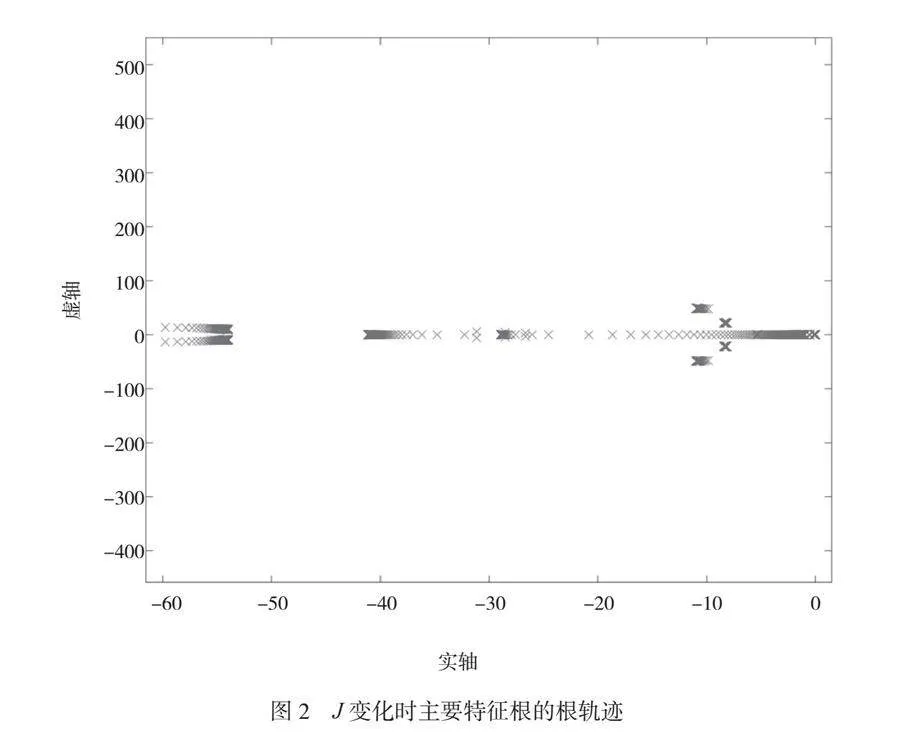
将所研究的参数在一定范围内进行变化，其他参数保持不变。J从0.5逐步增至20，主导特征值根轨迹如图2所示。

当转动惯量J从0.05增至20时，高频特性根基本不变，低频特性根的变化逐渐变慢。特征根和共轭特征根同时向左移动并远离虚轴，系统稳定性提高。

3.2 跟网型控制与构网型控制对根轨迹的影响对比

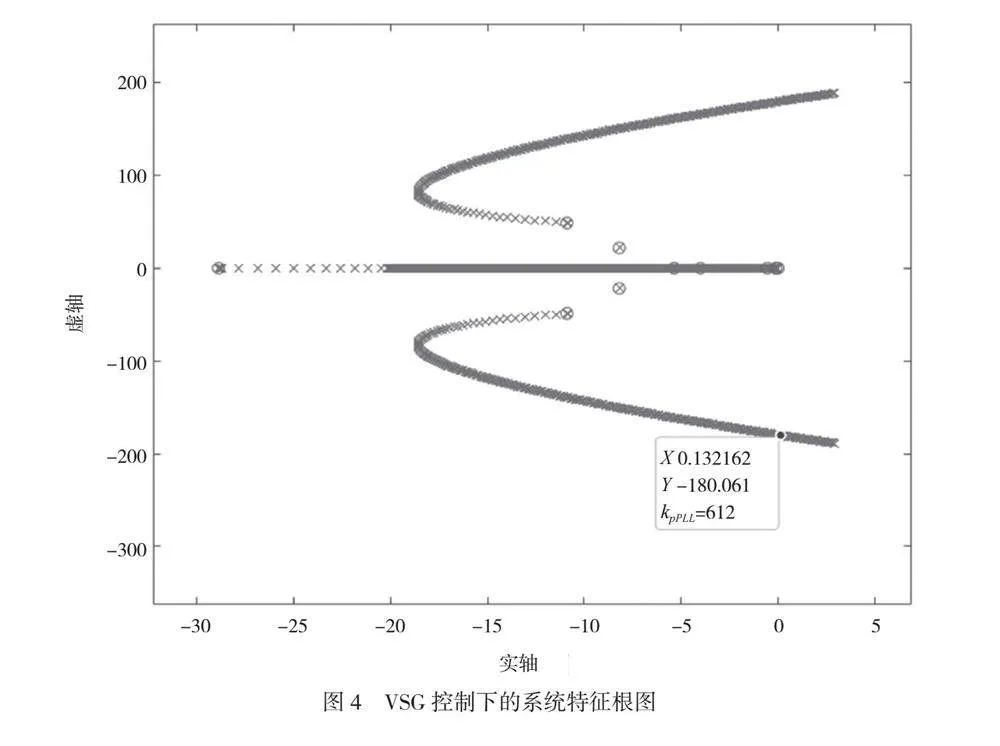
将本文采用的VSG控制方法与文献[9]中采用的VF控制（电压频率控制）进行比较，并改变风电场锁相环参数，观察2种不同控制方法下系统的稳定性，结果分别如图3、图4所示。采用VF控制的系统特征根在592处进入右半平面，采用VSG控制的系统特征根在612处进入右半平面。对比结果表明，2个根轨迹的波形基本相同。但采用VSG控制的系统具有更好的稳定性，由于其包括惯性回路，因此能为系统提供惯性支持。

4 结论

本文建立了海上风电场经VSC-HVDC送出系统的动态数学模型。风电场控制系统采用恒定直流电压和无功功率控制，整流侧控制系统采用VSG控制。并根据动态数学模型对整个系统进行了小扰动建模和特征值分析，探讨了惯性系数对系统稳定性的影响。最后通过比较跟网型控制与构网型控制对特征根轨迹的影响，验证了分析结果的正确性。

参考文献

[1]A KOROMPILI，Q WU，H ZHAO.Review of VSC HVDC connection for offshore wind power integration[J].Renewable and

sustainable energy reviews，2016（59）：1405-1414.

[2]肖朝霞，王成山，王守相.含多微型电源的微网小扰动稳定性分析[J].电力系统自动化，2009，33（6）：81-85.

[3]QU S，WANG Z.Cooperative control strategy of virtual synchronous

generator based on optimal damping ratio[J].IEEE Access，2021，9：709–719.

[4]裴继坤.直驱永磁风机经柔性直流输电并网的小干扰稳定性分析[D].北京：华北电力大学，2019.

[5]李文津，汤广福，贺之渊.DFIG风电场经模块化多电平柔性直流并网控制策略[J].电力系统自动化，2013，37（15）：20-26.

[6]邵冰冰.直驱风电场经柔直并网系统的振荡特性和抑制策略研究[D].北京：华北电力大学，2021.

[7]吴辉，阮晓东，杨东.虚拟同步发电机的小扰动建模与参数设计[J].电子工程学报，2016，63（1）：4292-4303.

[8]张杰，柔性高压直流系统小信号稳定性影响因素研究[D].北京：华北电力大学，2017.

[9]POGAKU，M PRODANOVIC，T C GREEN.Modeling analysis

and testing of autonomous operation of an inverter-based microgrid[J].

IEEE transactions on power electronics，2007，22（2）：613–625.

通信作者：李兰芳（1978-），女，湖北荆门人，博士，高级工程师，研究方向为柔性交/直流输配电成套电力电子装备关键技术。

电子邮箱：lilanfang@sgepri.sgcc.com.cn。