基于DECWOA的配电网故障定位技术要点探究

摘 要：本研究的主要目的是提高配电网故障定位技术的精确性，针对鲸鱼优化算法存在的局部寻优与全局优化不平衡问题，通过引入差分进化算法，提出了混沌鲸鱼优化算法（DECWOA）。试验表明，与传统鲸鱼优化算法相比，DECWOA在配电网故障定位中的定位精确度更高。该研究为提高配电网故障定位的准确性和效率提供了一种新的方法，为故障定位问题提供了更可靠的解决方案，这一研究成果对电力系统的稳定运行具有积极的推动作用。

关键词：DECWOA；配电网故障定位；Sine映射

中图分类号：TM 73 " " " " 文献标志码：A

当面对复杂多变的电力系统时，传统的故障定位方法存在一定的局限性，例如难以有效地对多节点同时发生信息畸变的情况进行处理。为了解决这个问题，本研究聚焦引入改进的鲸鱼优化算法（DECWOA）来优化配电网故障定位技术。DECWOA基于原始的鲸鱼优化算法（WOA）并通过3种有效的改进策略提高了其在寻优过程中的性能，尤其是防止陷入局部最优状态的问题。本研究旨在深入探究DECWOA在配电网故障定位中的应用要点，对其性能和有效性进行分析和试验验证。

1 鲸鱼优化算法的改进策略

1.1 Sine映射初始化种群

在本次研究中，相关研究人员尝试对鲸鱼优化算法进行改进，通过引入混沌映射来提高算法的精度和收敛速度。在具体实践中，研究人员考虑了2种混沌映射方式，即Logistic映射以及Sine映射，试验发现，Logistic混沌映射导致初始化种群主要集中在区域的右上部分和边界处，Sine混沌映射导致初始化种群分布相对均匀[1]。Sine混沌映射具有明显的混沌特性，能够有效避免初始化个体集中分布，有助于提高种群的多样性和搜索效率，Sine混沌映射的表达式如公式（1）所示。

（1）

式中：xn为第n次迭代时的变量值或状态。

xn随着迭代次数n逐步更新，通过混沌映射的计算来生成新的搜索点或个体的值。在本次研究中，xn+1初始值不为0，当映射迭代次数达到一定程度时，混沌映射个体分布充满整个解空间。

1.2 自适应惯性权重

在本次研究中，相关研究人员为了提高算法的优化效率和全局收敛能力，引入“自适应惯性权重”概念，这一概念的核心是在算法迭代过程中根据不同阶段的需求动态调整惯性权重的大小，以实现更高效的优化，研究人员设自适应惯性权重为ω，其计算过程如公式（2）所示[2]。

ω=0.5+exp（-ffit（x）/u）t nbsp; " " " "（2）

式中：ffit（x）为个体x的适应度数值；u为首次迭代优化全局最优适应度；t为迭代次数。

1.3 融合差分进化算法

在本次研究中，研究人员在保留鲸鱼优化算法优良特性的基础上，引入差分进化变异以及交叉操作。在差分进化算法中，每个个体被表示为一个向量，通常称为目标向量[3]。算法的核心是通过差分变异来生成新的个体，然后使用二项式交叉操作来更新目标向量。在本次研究中，相关研究人员针对每个目标向量，选择其他3个不同的个体来计算它们的差分向量。差分向量表示个体之间的差异，计算过程如公式（3）所示。

vid=xr1+F·（xr2-xr3） " " " "（3）

式中：vid为第d维度的变异个体数量；xr1、xr2、xr3为鲸鱼种群中随机挑选的个体，借助变异因子形成新的变异矢量；F为变异因子。

研究人员在此基础上进行二项交叉并得到试验向量，通过这种方式保留目标向量和变异向量的有用信息，计算过程如公式（4）所示。

（4）

式中：uid为第d维度试验体个数；rand[0，1]为[0，1]中的随机数；CR为交叉概率因素，其取值范围为[0，1]。

1.4 改进算法的步骤与流程

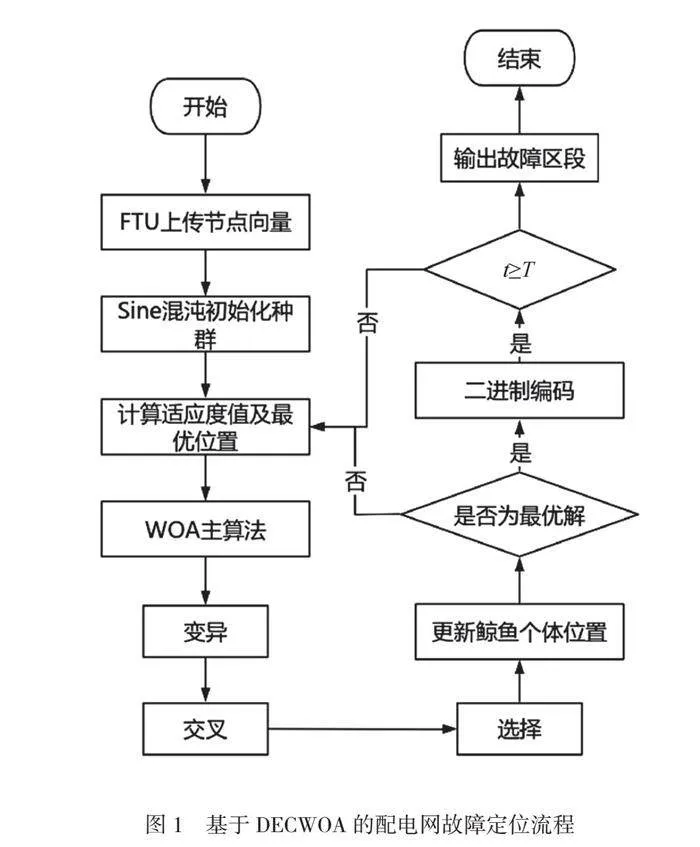
在本次研究中，相关研究人员基于差分进化算法以及鲸鱼优化算法，提出了一种新的配电网故障定位流程。该流程充分利用了自适应惯性权重和Sine映射混沌技术，以提高算法的全局搜索和局部优化能力。从微观层面来看，基于DECWOA的配电网故障定位流程主要分为以下9个步骤（如图1所示）。

1.4.1 设置参数

研究人员设定最大迭代次数为T，当前迭代次数为t，求解问题的维度为D，种群规模为N。

1.4.2 初始化种群

引入Sine映射混沌对鲸鱼种群进行初始化。Sine映射是一种经典的混沌映射，可以有效提高种群的多样性[4]。通过该步骤，研究人员得到了1组具有随机性的鲸鱼个体，为后续的搜索过程提供多样性。

1.4.3 更新鲸鱼位置

根据鲸鱼算法的寻优原理，计算概率因子p、系数|A|和自适应惯性权重O的值，通过这种方式更新鲸鱼个体的位置，引导鲸鱼在搜索空间中进行局部和全局搜索。

1.4.4 计算适应度值

计算每个鲸鱼个体的适应度值f，并记录最优鲸鱼的位置xbest及其对应的全局最优适应度值fbest。这一步骤有助于评估鲸鱼个体的优劣，并为后续的迭代提供参考。

1.4.5 变异操作

随机选取种群中互不相同的目标向量xi1、xi2、xi3，生成新的变异向量vid，通过引入新的变异基因，保持种群的多样性。

1.4.6 交叉操作

研究人员通过二项交叉操作将原目标向量以及变异向量生成新的试验向量uid，通过这种方式在种群中传播优良基因，提高搜索效率。

1.4.7 更新鲸鱼位置

基于试验向量uid和适应度值f来更新鲸鱼个体的位置。通过比较ffit（uid（t））与ffit（xid（t））的大小，确定是否更新位置。

1.4.8 适应度值计算

重新计算所有鲸鱼个体的适应度值，并比较当前全局最优适应度值fbest与新的适应度值，如果新适应度值更优，就更新fbest、gbest。

1.4.9 迭代终止条件

当迭代次数t达到最大迭代次数T时，算法终止。否则，返回步骤3，继续进行迭代。

2 算法性能测试与分析

为了验证上述算法的有效性，研究人员在实验室中搭建了完整的试验环境，使用MATLAB R2020b仿真软件，将D设为30，种群规模为40，研究人员考虑随机误差问题，将独立循环次数设为40次，最大迭代次数为600，取40次试验数据并计算平均值以及标准差，通过这种方式对每一种改进策略的贡献度进行横向对比[5]。

2.1 基准测试函数

在本次研究中，相关工作人员将CEC2023函数集作为基准测试函数，该函数集拥有多模态空间特征。研究人员利用充分性测试对测试结果进行比较（见表1）。

在表1中，F1、F2、F3、F4、F5代表单峰函数，其主要作用是判断DECOWA算法的收敛速度，F6、F7、F8、F9、F10代表非线性多峰函数，其主要作用是判断DECOWA算法的全局开发能力，F11、F12、F13、F14代表维数不变的多峰函数，其主要作用是计算DECOWA算法局部搜索能力。

2.2 改进策略的贡献度分析

在本次研究中，相关工作人员通过比较不同改进策略的效果来验证这些策略的合理性和优越性。其中，WOA-1为原始的鲸鱼算法，WOA-2为Sine混沌种群初始化的WOA算法，WOA-3为自适应惯性权重策略，WOA-4为融合差分进化算法。

研究人员比较WOA-2与基本WOA-1的性能差异，观察初始种群的分布均匀性和对全局搜索的影响[6]。如果WOA-2比WOA-1表现更好，那么说明Sine混沌种群初始化对全局搜索能力的提升有贡献，其原因是Sine混沌映射能够有效避免个体集中分布，提高了种群的多样性。而比较WOA-3与WOA-1的性能，更多的是判断惯性权重调整对全局和局部搜索的影响，以及在不同阶段的适应性。如果WOA-3比WOA-1表现更好，那么说明自适应惯性权重的引入对算法的动态调整有益，其原因是该策略在全局搜索和局部搜索阶段实现了合理的平衡。当WOA-4与WOA-1进行比较时，研究人员着重关注融合差分进化算法对算法的收敛速度和全局优化能力的影响。如果WOA-4比WOA-1表现更优，那么说明融合差分进化算法对改善全局搜索能力更具有效果，其原因是引入差分进化算法的弥补了原始WOA在全局搜索上的不足。研究人员通过对F1～F14融合改进策略寻优结果的综合对比得出以下结论。

加入改进策略的算法在很大程度上提升了WOA的优化性能。在测试函数F7、F9、F13和F14中，WOA-3和WOA-4均能够达到理论最优值。虽然WOA-3和WOA-4的优化能力相近，但是WOA-4的性能更稳定[7]。对测试函数F5、F7和F11来说，WOA-1的寻优效果比WOA-2好，其原因是改进惯性权重策略在提高算法收敛速度的同时，也提高了算法的局部搜索能力。而在测试函数F4中，WOA-3的寻优效果比WOA-4好。这表明在特定问题上，WOA-3的优化策略更具优势。在测试函数F12中，WOA-2的寻优效果比WOA-3好。然而，在30次计算中，WOA-3的最优值更接近理论最优值，说明WOA-3在某些情况下，具有更高的搜索效率。从整体上看，3种改进策略均在不同程度上提高了WOA的优化性能。其中，WOA-4（融合DEC改进）在计算能力上改善最大，其次是改进惯性权重的WOA-3，最后是Sine混沌优化初始种群的WOA-2。这表明DECWOA在综合性能上具有优势，可以更好地应对复杂优化问题。因此，DECWOA可以视为一种以融合DEC为主体、以改进惯性权重和融合Sine混沌映射为辅助手段的多策略改进算法。

2.3 与其他算法性能对比

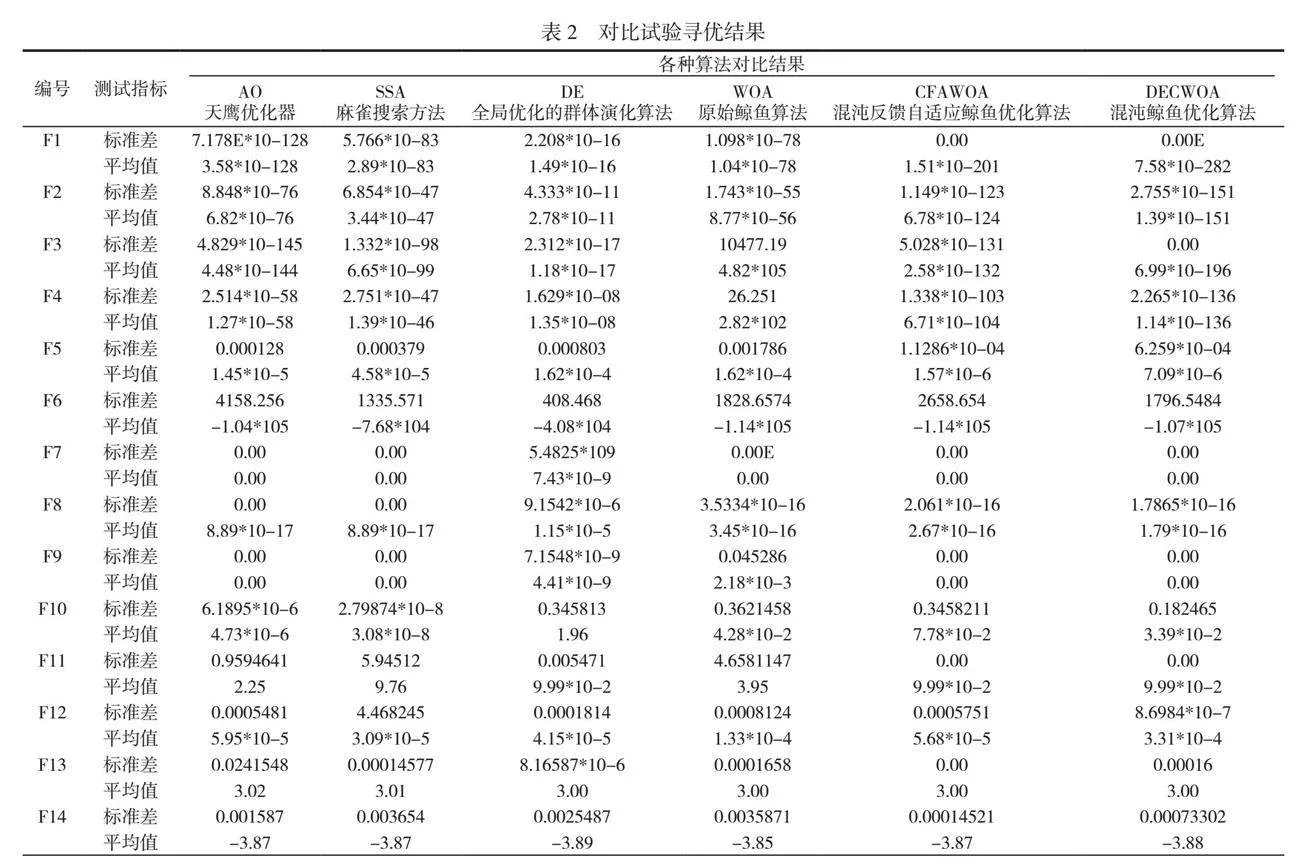
除了分析改进策略贡献度之外，研究人员还引入了几种常见的智能算法与DECWOA进行横向对比。为了尽可能减少误差，研究人员对F1～F14函数进行独立测试，测试共计进行30轮，统计测试函数的标准差与平均值（见表2）。

分析表2中的数据可以发现，在单峰测试函数F1～F5的优化研究中，DECWOA展现出了卓越的计算精度和稳定的性能，其标准差最小，说明该算法在应对不确定性问题时具有较高的鲁棒性，DECWOA在实际应用中能够适应各种复杂环境，为优化问题提供可靠的解决方案[8]。在非线性多峰测试函数F6～F10优化问题上，DECWOA表现出了优异的寻优效果和强大的全局开发能力。其寻优平均值比其他对比算法高，显示DECWOA在解决复杂多峰优化问题时具有较高的竞争力，这就为DECWOA在实际工程中的应用提供了有力的依据。然而，在固维多峰测试函数F10和F12中，DECWOA的寻优平均值比SSA和AO算法略低，这表明DECWOA在局部探索能力方面还有待提高。为了进一步提高DECWOA的性能，研究者们可以在算法改进中重点关注局部搜索策略的优化。

从整体上看，改进后的DECWOA在优化精度上取得了显著提升，特别是在单峰测试函数F1～F5中表现突出。试验数据证实了DE（差分进化）算法的计算精度比基本的WOA（鲸鱼优化算法）高，但比DECWOA低。通过对比试验结果的收敛曲线可以看出，DECWOA具有更高的寻优精度和更快的收敛速度，且不易陷入局部最优状态。在多种测试函数中的表现证实了DECWOA相较于其他算法的优势，特别是在F12和F14中成果尤为显著。DECWOA的改进策略成功避免了WOA陷入局部最优状态，从而提高了寻优精度和收敛速度。这为DECWOA在实际应用中提供了有力的支持，有望成为解决优化问题的有力工具。

3 结语

在本次研究中，为解决基于WOA算法的配电网故障定位过程中容易陷入局部最优的问题，相关工作人员提出了基于DECWOA算法的故障定位策略。通过试验证明，DECWOA在大多数情况下均具有更快的收敛速度和更高的精度，证实了其在解决复杂优化问题方面的优势。同时，研究人员还分析了DECWOA在处理具有多峰特性的函数时改进策略对其寻优性能的提升作用，从而进一步说明了DECWOA在实际应用中的适用性。在今后的研究中，研究人员将继续探索更多有效的改进策略，以提高WOA的性能，为实际问题的解决提供更优质的服务。

参考文献

[1]齐郑，黄朝晖，陈艳波.基于零序分量的阻抗法配电网故障定位技术[J].电力系统保护与控制，2023，51（6）：54-62.

[2]刘杰荣，张耀宇，关家华，等.基于量测大数据和数学形态学的配电网故障检测及定位方法研究[J].智慧电力，2020，48（1）：97-104.

[3]余修勇，肖立业.直流配电网故障识别和定位技术研究综述[J].电工电能新技术，2019，38（7）：56-66.

[4]李振兴，孟晓星，李振华，等.应用等效网络原理的新型配电网故障定位技术[J].电力系统及其自动化学报，2019，31（1）：31-39.

[5]王秋杰，金涛，谭洪，等.基于分层模型和智能校验算法的配电网故障定位技术[J].电工技术学报，2018，33（22）：5327-5337.

[6]刘健，张志华，陈宜凯，等.适用于含DG配电网故障处理性能测试的主站注入测试技术[J].电力系统自动化，2017，41（13）：119-124，132.

[7]程学珍，林晓晓，朱春华，等.含分布式电源的配电网故障诊断方法[J].工矿自动化，2017，43（4）：55-59.

[8]吴骏，王震，袁海星，等.基于物联网技术的配电网故障定位研究[J].高压电器，2015，51（12）：72-78.