见微知著：代数式中蕴含的数学思想方法

进入“代数式”这一章的学习，我们开始体验从“算术”到“代数”的飞跃。在学习过程中，我们可以发现算术和代数的联系与区别，也能逐步感受代数的特点：抽象性、简洁性、一般性。本章需要掌握的主要概念包括代数式、整式、单项式、多项式、代数式的值、同类项等。同时，我们在研究代数式的相关运算时也离不开数的运算，有些学习经验可以进行类比迁移。

作为初中数学代数板块的起始内容，代数式是我们后面研究方程、不等式、整式乘法、分式、二次根式、函数等内容的基础，起着“统领全文”的作用。而代数式中所蕴含的数学思想方法贯穿我们初中数学学习的始终，需要我们重点关注和深入研究。

分类讨论

例1 比较a+b与a-b的大小。

【解析】比较代数式的大小，我们可以采用作差法。（a+b）-（a-b）=2b。其中，b可以取任意值，因此这两个式子的大小关系不确定，我们需要分三种情况讨论：当b＞0时，a+b＞a-b；当b＜0时，a+b＜a-b；当b=0时，a+b=a-b。

比较两个数的大小，结论是确定的。而代数式中的字母可以取任意值，所以在一般情况下，我们无法直接比较两个代数式的大小。此时，我们可以先作差，然后对作差的结果进行分类讨论，但要注意讨论过程中不要出现重复或者遗漏等情况。

整体思想

例2 已知代数式x2-2x+3的值是7，则代数式-4x+2x2的值是 。

【解析】一般情况下，我们需要知道代数式中所含字母的值，然后将其代入代数式求值，比如本例中知道x的值即可。根据已知条件，得x2-2x+3=7。以我们目前的知识储备无法直接解这个方程，也就无法知道x的具体值。但是我们可以得到x2-2x=4。如果将x2-2x看成一个整体，所求代数式-4x+2x2的值正好是x2-2x的两倍，所以得到代数式-4x+2x2的值是8。

求代数式的值，我们除了将代数式中所含字母的值代入，还可以根据已知条件进行变形，然后整体代入求值。这就是整体思想的魅力。

猜想归纳

例3 观察下列关于x的单项式，探究其规律：x，4x3，9x5，16x7，25x9……按照上述规律，第n项是 。

【解析】此类题型考查通过猜想归纳发现所列代数式的规律。我们一般从以下角度观察：系数、字母、字母的指数，即单项式的各项要素。通过观察，我们猜想系数为n平方，字母都是x，字母的指数为2n-1，由此我们归纳出第n项为n2x2n-1。

猜想归纳是非常重要的数学思想，对于研究问题、发现规律有着重要的作用。我们要学会在观察的基础上发现问题本质，大胆猜想、谨慎归纳、小心论证。

数形结合

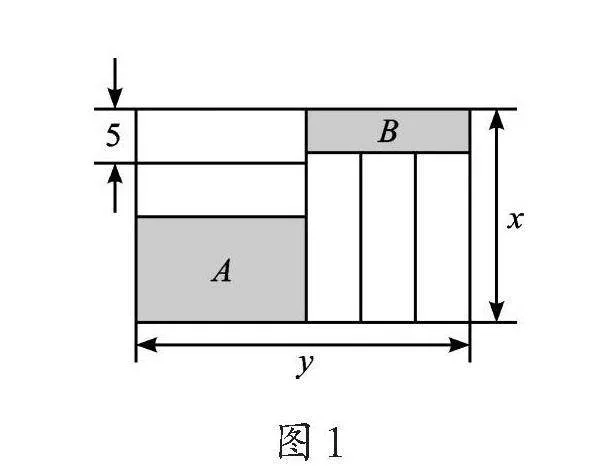
例4 如图1，长为y（cm），宽为x（cm）的大长方形被分割为7小块。除阴影A、B外，其余5块是形状、大小完全相同的小长方形，其较短的边长为5cm，则阴影A的较短边和阴影B的较短边之和为（ ）。

<D：＼JR工作＼初中生＼7年级＼11＼王张毅-1.tif>

图1

A.x-y+5 B.2x+y+5

C.2x-y+5 D.x+y+5

【解析】结合图形中所蕴含的边与边之间的数量关系，我们可以分别表示出A的较短边长为x-10，阴影B的较短边长为x-（y-15），然后相加得到所求的两条边之和为2x-y+5。故选C。

矩形是沟通代数与几何的重要桥梁之一。通过代数式对矩形周长和面积的表示，我们可以更加直观地感受代数式所蕴含的实际意义。在后续学习整式的乘法时，我们能够更加深切地感受这一点。

数学思想是掌握和运用数学知识的强大工具。在学习数学的过程中，我们应当努力发现并深刻理解这些思想，如分类讨论、整体思想、归纳推理、数形结合等。随着学习的深入，我们还将逐渐接触到更多数学思想，例如类比推理、问题转化、从特殊到一般等，这些丰富的思想将为我们的数学学习之旅增添更多色彩。

（作者单位：江苏省南京市宁海中学分校）