不确定环境下医疗废物回收网络鲁棒优化研究

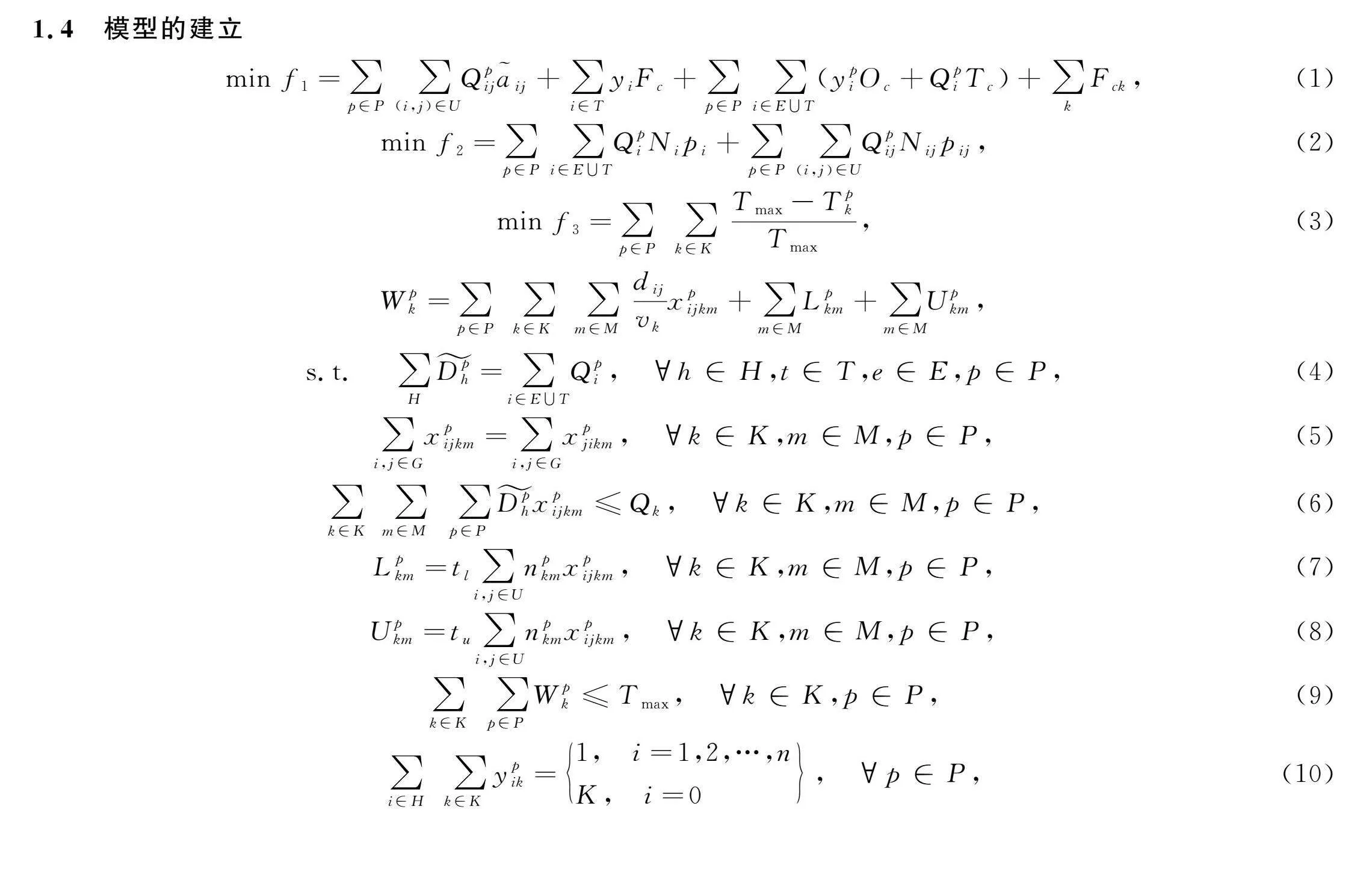
摘 要：针对医疗废物回收网络的不确定性，选取医疗废物量和运输成本作为关键变量，构建有多个不确定参数的多目标非线性整数规划模型，并引入鲁棒优化来处理不确定因素。结合多目标粒子群优化算法（MOPSO）和遗传算法（GA）求解该模型，外层GA负责选址决策，内层MOPSO针对选址结果进行配送路径优化，并以国内某城市为实证对象进行仿真验证。结果表明：相较于传统遗传算法，所提算法总成本降低了10.37%，总风险减少了1.86%，工作量偏差缩减了50.18%；敏感性分析表明，医疗废物量的不确定性对目标函数的影响更为显著。所提模型使得决策者可根据风险偏好调整不确定参数，以获得最佳的医疗废物回收网络优化方案，为进一步的医疗废物回收研究提供了参考。

关键词：城市运输经济学；医疗废物；回收网络；鲁棒优化；多目标粒子群优化算法

中图分类号：U121

文献标识码：A

DOI：10.7535/hbkd.2024yx05010

Robust optimization of medical waste recycling

network in uncertain environment

LI Changbing，LIANG Qin， WU Ling

（School of Economics and Management， Chongqing University of Posts and Telecommunications， Chongqing 400065， China）

Abstract：Aiming at the uncertainty of medical waste recycling network， with the quantity and transportation cost of medical waste as the key variables， a multi-objective nonlinear integer programming model with multiple uncertain parameters was constructed， and robust optimization was introduced to deal with the uncertain factors. Multi-objective particle swarm optimization （MOPSO） and genetic algorithm （GA） were combined to solve the model. The outer GA was responsible for location decision， and the inner MOPSO was responsible for distribution path optimization based on location selection results. A domestic city was selected as the empirical object for the simulation. The results show that compared with the traditional genetic algorithm， the proposed algorithm reduces the total cost by 10.37%， the total risk by 1.86% and the workload deviation by 50.18%; Sensitivity analysis proves that the uncertainty of medical waste volume has more significant influence on the objective function. The proposed mode can help the decision makers adjust the uncertain parameters according to the risk appetite to obtain the best medical waste recycling network optimization scheme， which provides some reference for further study of medical waste recycling.

Keywords：urban transportation economics; medical waste; recycling network; robust optimization; multi-objective particle swarm optimization algorithm

医疗废物携带大量病菌，管理不善会威胁健康与环境[1]。为确保公共卫生安全，需构建医疗废物回收网络，但回收环节复杂多变，涉及成本[2]、废物量[3]等因素。为解决这些问题，学术界常用的有模糊规划、随机规划和鲁棒优化等技术。模糊规划因适应性强，常用于处理不确定性问题。例如BABAEE等[4]提出模糊需求下的双目标模型，并采用多目标入侵杂草优化算法和ε约束方法求解；JONEGHANI等[5]从可持续发展的角度，构建了不确定性条件下的多目标混合整数线性规划模型。随机规划能描述随机情境的不确定性。例如：蒲松等[6]研究离散随机参数下的医疗回收网络问题，并采用BD（benders decomposition）加速方法求解；YU等[7]以人口为随机参数，用样本平均近似-遗传编程方法求解，验证随机模型更能应对环境变化。鲁棒优化在随机规划基础上分析不确定集合和离散情境。例如：ZHAO等[8]针对新冠疫情期间废物问题，用基于场景的双目标鲁棒优化方法求解；KARGAR等[9]用鲁棒优化控制医疗废物量的不确定参数，建立多目标混合整数规划模型。

目前对于医疗废物回收网络的研究主要有2方面：一是运用多准则决策方法来评价回收过程。如MISHRA等[10]提出多准则复杂比例评价法选择危险废物回收设施地址；GHOUSHCHI等[11]用球面模糊集扩展多标准决策来选择医疗废物填埋场，MI等[12]用带有幂次有序加权平均算子的软似然函数描述决策者的偏好，并将其运用到医疗废物管理方法中；二是构建医疗废物回收网络。如YU等[13]提出了一种多目标多周期混合整数规划，用于流行病逆向物流网络设计；TIRKOLAEE等[14]开发了一种多目标混合整数规划模型，以研究新冠疫情期间医疗废物的可持续选址路径问题；李欣等[15]考虑了时间、风险和成本，提出了基于医院、中转点、处理中心联动的三级运输网络优化模型；鲍秀麟等[16]从政府、公众和处理中心承包商角度设计改进的多目标樽海鞘算法，以解决医疗废物处理中心的选址路径问题。

综上所述，现有研究在医疗废物回收网络建模时通常仅考虑单一不确定因素，但实际情况复杂得多。医疗废物量受医疗机构和患者流量的影响，运输成本则与废物量、燃油和交通状况相关。为减少不确定性，本文聚焦医疗废物量和运输成本，采用鲁棒优化处理。同时，考虑医疗废物对回收人员的潜在危害[17]，从社会效应、经济成本和运输风险角度构建多目标非线性混合整数优化模型，并结合多目标粒子群算法和遗传算法优化回收网络，最后通过实例验证算法的有效性。

1 问题描述及模型构建

1.1 问题说明

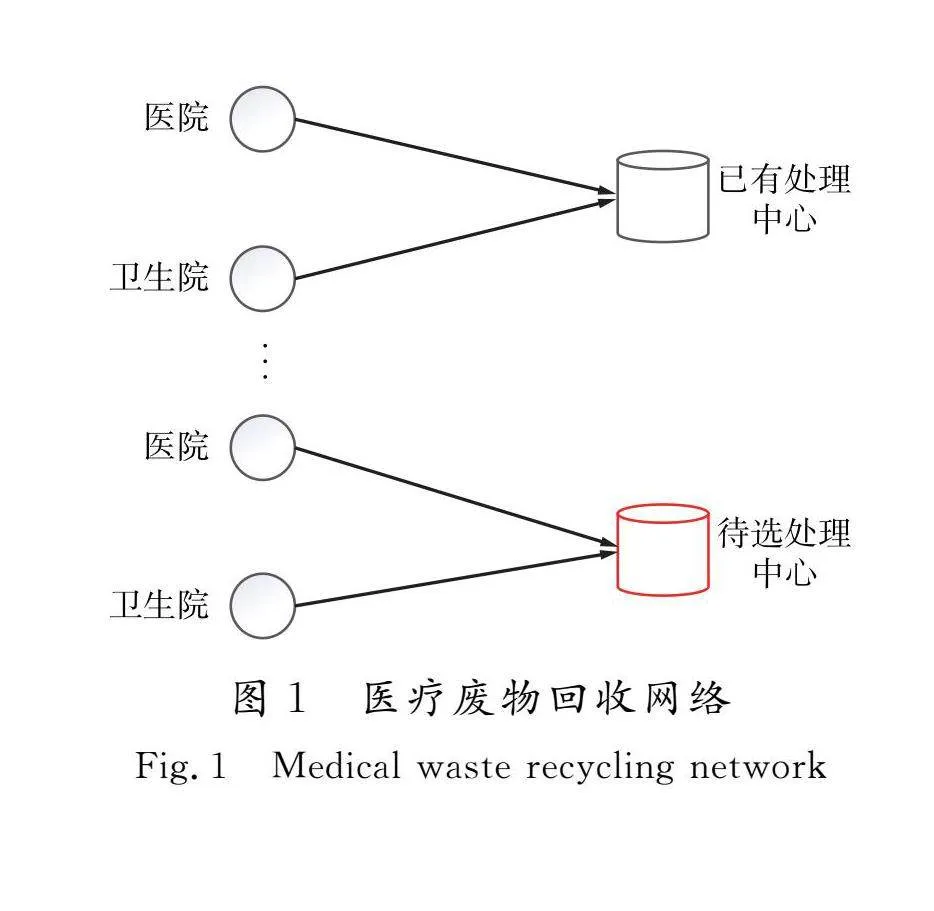
如图1所示，本文所构建的医疗废物回收网络是由医院和回收处理中心组成的二级回收网络。在此回收网络中，每个周期有专门的车辆将各医院和卫生院产生的医疗废物运送至医疗废物处理中心集中处理。图2给出了运输车辆在此网络中任意一周期内的运输路线示例。在一个回收周期内，车辆1先从停车场出发至医院收集医疗废物，然后驶入医疗处理中心卸载收集来的废物，以此完成车辆的一次行程。而倘若有下个行程，则直接以处理中心为起点，重复医院到处理中心的转运工作，直至所有医院所产生的医疗废物被转运完，最后返回停车场。为了完成一个周期内医疗废物的收运工作，考虑使用多辆运输车按照上述路线依次完成收运工作。

1.2 模型假设

1）医疗废物在运输及处理过程中产生的风险和人口密度、运输距离及医疗废物的数量正相关，且具有可加性。

2）网络中每家医院由1辆车所覆盖。

3）每辆车从停车场开始其第1次行程，并依次前往医院装载医疗废物，直至将医疗废物运送至医疗废物处理中心才结束。然后从处置中心开始可能的第2次行程，并再次结束。

4）医疗废物处理中心的运营成本和处理的危险医疗废物数量呈线性相关。

5）车辆存在最长可用服务时间。

1.3 参数设置

参数符号定义见表1。

1.4 模型的建立

min f1=∑p∈P

∑（i，j）∈U

Qpijij+∑i∈T

yiFc+

∑p∈P

∑i∈E∪T（ypiOc+QpiTc）+

∑kFck，（1）

min f2=∑p∈P∑i∈E∪TQpiNipi+

∑p∈P∑（i，j）∈U

QpijNijpij，（2）

min f3=∑p∈P∑k∈KTmax-TpkTmax，（3）

Wpk=∑p∈P∑k∈K∑m∈M

dijvkxpijkm+∑m∈MLpkm+∑m∈MUpkm，

s.t. ∑HDph=∑i∈E∪TQpi， h∈H，t∈T，e∈E，p∈P，（4）

∑i，j∈Gxpijkm=∑i，j∈Gxpjikm， k∈K，m∈M，p∈P，（5）

oXPuPbsLLgN4XPqQWZCZ+g==

∑k∈K∑m∈M∑p∈PDphxpijkm≤Qk， k∈K，m∈M，p∈P，（6）

Lpkm=tl∑i，j∈Unpkmxpijkm， k∈K，m∈M，p∈P，（7）

Upkm=tu∑i，j∈Unpkmxpijkm， k∈K，m∈M，p∈P，（8）

∑k∈K∑p∈PWpk≤Tmax， k∈K，p∈P，（9）

∑i∈H∑k∈Kypik=1， i= …，nK， i=0， p∈P，（10）

∑i，j∈V∑m∈Mxpijkm≤Axpk， k∈K，p∈P，（11）

∑k∈K∑m∈M（xpijkm+xpjikm）=1， （i，j）∈U，p∈P，（12）

∑j∈Hxp1jkm=ypk， k∈K，m=1，p∈P，

∑j∈H∑i∈Expjikm=ypk， k∈K，m=1，p∈P，（13）

∑i∈S∑j∈S，i≠jxpijkm≤|S|-1， S∈V，S≠，k∈K，m∈M，p∈P，（14）

Qpi≤ypiMi， i∈{E，T}，p∈P，（15）

ypi≤yi， i∈T，p∈P，（16）

∑p∈Pypi≥yi， i∈T，（17）

yp-1i≤ypi， i∈T，p∈P，（18）

ypi-yp-1i≤yi， i∈T，p∈P，（19）

∑p∈Pypi≥1， i∈{E，T}，（20）

dpij，Qpi，Lpkm，Upkm≥0， i，j∈U， k∈K，m∈M，p∈P，（21）

yi，ypi，xpijkm，ypk∈{0，1}， i∈{E，T}， k∈K，m∈M，p∈P。（22）

式（1）为总经济成本（元），包括运输成本、建设成本、运营成本和车辆使用成本；式（2）为总风险（人·t），主要由处理风险和运输风险构成；式（3）为工作量偏差，该目标通过平衡各时间段内车辆的总服务时间，使工作量偏差最小化，即最大限度地提高员工的满意度。式（4）表示处理中心的流量平衡；式（5）表示车辆网络中流量平衡；式（6）表示车辆在每次行程中的容量限制，t；式（7）和式（8）计算第k辆车在第m次行程和第p个周期的总装载时间、总卸载时间；式（9）为车辆的最大可使用时间，h；式（10）表示医疗废物运输车辆的数目为K；式（11）表示车辆在已经分配时才能构建路线；式（12）确保所需边缘仅由1辆车提供；式（13）保证车辆应从停车场开始第1次行驶，并在处置场结束；式（14）消除任何可能的子行程；式（15）表示处理中心e和新建处理中心t的容量限制，t；式（16）表示新建处理中心t的选择和运行期；式（17）保证新建处理中心t被使用次数多于开放次数；式（18）表示新建处理中心t如被使用，该中心就要运营到时间周期结束；式（19）表示新建处理中心t被使用，该中心必须是开放的；式（20）保证至少选择1个处理中心e和新建处理中心t；式（21）和式（22）分别表示各决策变量为非负变量和0-1变量。

2 遗传多目标粒子群算法设计

2.1 模型处理

1）车辆行驶速度的动态处理

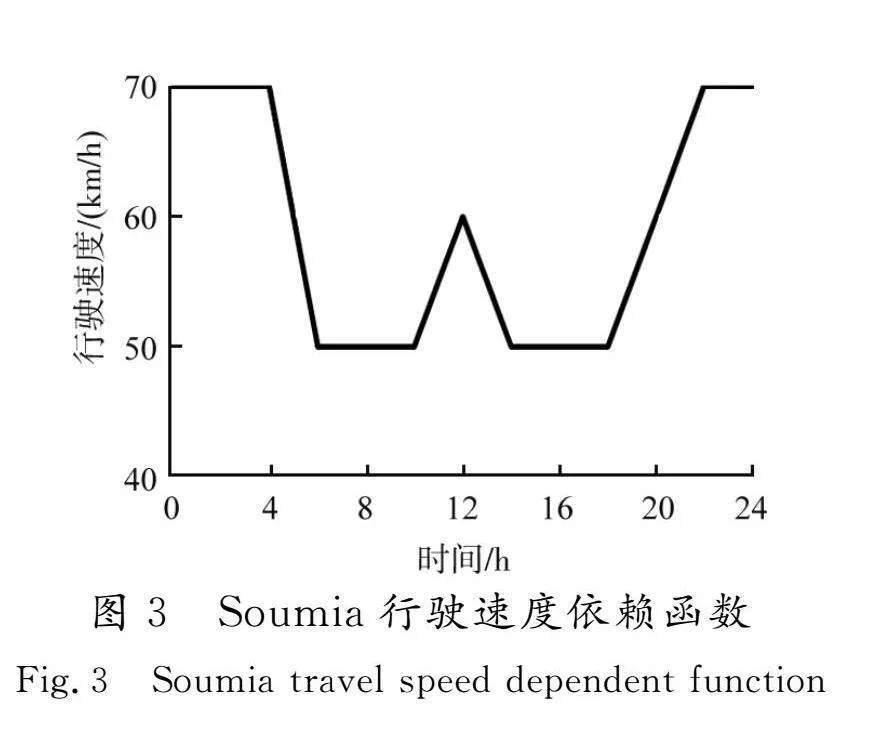
车辆行驶途中存在诸多干扰因素，车辆很难保持匀速行驶，因此为了能更好地刻画运送医疗废物的车辆的行驶速度，考虑借鉴SOUMIAtffu等[18]提出的速度依赖函数（见图3）来描述车辆在早高峰和晚高峰连续行驶时期车速的时刻变化。

2）不确定参数的处理

由于所构建的模型内含有2个不确定参数，所以导致目标函数f1不具有明确意义且约束条件不清晰。对于此类不确定环境下的复杂问题，采用鲁棒线性规划方法将参数的不确定性转化为可求解的线性模型。将2个不确定参数用区间数进行定义，如单位运输成本

ij和医疗废物量Dpt，分别定义其名义值和最大偏离值[19]。将带有不确定参数的模型转化为鲁棒优化模型。具体的鲁棒优化处理过程如下。

步骤1：单位运输成本不确定的鲁棒优化处理

定义不确定参数ij范围为［ij-ij，ij+ij］，其中ij和ij分别代表名义值和其最大偏离值。参照文献[19]对不确定参数的处理，引入辅助变量f，目标函数f1等价于：

min f，（23）

∑p∈P∑i∈U∑j∈U

Qpijij≤f-∑i∈TyiFc-∑p∈P∑i∈E∪T

（ypiOc+QpiTc）-∑kFck。（24）

引入保护函数：β（Z，Γi）=max{Si∪ti|SiBi，|Si|=Γi，ti∈Bi＼Si}

∑j∈SiQpijij+（Γi－Γi）itiQpij。

Γi是不确定性预算，属于控制系数，所属范围为［0，|Bi|］，故：

∑p∈P∑i∈U∑j∈U{Qpijij+β（Z，Γi）}≤f-

∑i∈TyiFc-∑p∈P∑i∈E∪T（ypiOc+QpiTc）-

∑kFck。（25）

将保护函数转化为线性规划模型，且根据强对偶理论，式（25）可转化为

∑p∈P∑i∈U∑j∈U{Qpijij+

∑j∈Bipij+ΓiZi}≤f-∑i∈TyiFc-∑p∈P

∑i∈E∪T（ypiOc+QpiTc）-∑kFck，（26）

s.t. pij+Zi≥Qpijij， j∈Bi，

pij≥0， j∈Bi， i，

Zi≥0， i。（27）

步骤2：对医疗废物量的鲁棒优化处理

对式（4）和式（6）进行处理：

∑i∈E∪TQpi≥∑i∈Hpi+Γpi

|J|pi， i∈H，t∈T，e∈E，p∈P，（28）

Qk≥∑k∈K∑m∈M∑p∈P（pi+Γpi

|J|pi）xpijkm， k∈K，m∈M，p∈P。（29）

综上，本文所建立的含有2个模糊参数的模型就转化为以下的确定性线性规划模型：

min f，（30）

min f2=b10c543b4933f3b68cdfa2a755daedb7∑p∈P∑i∈E∪TQpiNipbi+∑p∈P

∑i，j∈UQpijNijpbij，（31）

min f3=∑p∈P∑k∈KTmax-WpkTmax ，

Wpk=∑p∈P∑k∈K∑m∈Mdijvkxpijkm+∑m∈MLpkm+∑m∈MUpkm，（32）

s.t. 式（5）、式（7）—式（22）、式（26）—式（29）。

2.2 算法设计

本文模型是多目标非线性整数规划模型，属于NP-hard问题。针对问题类型和模型特点，选择多目标粒子群优化算法MOPSO

（multi-objective particle swarm optimization algorithm）来求解。相较于标准粒子群算法，多目标粒子群优化算法引入了Pareto Dominance的概念，在寻优过程中将每个粒子的历史非支配解保存在外部储存库中，同时进行粒子的矢量速度和位置迭代。而对于外部存储库的维护，关菲等[20]提出将NSGA-Ⅱ（non-dominated sorting genetic algorithm Ⅱ）中拥挤距离排序和非支配排序思想用于外部存储库的更新。具体的维护方案如下：将每次算法迭代产生的新种群和外部存储库中的非劣解进行排序，如果新种群不受外部存储库中的元素支配，则加入外部存储库，否则便忽略。每次算法更新迭代都重复以上过程，直到新产生种群没有非劣解时，完成整个外部存储库的更新，并对外部存储库中的非劣解进行拥挤距离排序。

经过以上操作，MOPSO能避免陷入局部最优。不过该算法在搜索过程中信息交流和协同合作不够充分，导致难以快速找到全局最优解。因此为了提高求解速度，利用遗传算法（GA）具有多种群并行优化的特点，将两者相结合，设计GA-MOPSO（genetic algorithm-multi-objective particle swarm optimization algorithm）优化算法进行求解。算法逻辑是：首先，利用GA进行设施选址处理，将GA的选址结果作为MOPSO的输入，然后完成运量分配和路线选择，最后再将优化结果反馈给GA，从而完成模型的求解。

具体的算法求解过程如下。

step1：初始化相关数据和参数，进行二进制编码，随机生成一组0-1变量作为初始种群。选择该位置对应的候选站点为1，否则为0。

step2： 根据鲁棒优化处理后的模型计算GA初始种群的适应度函数。

step2.1：初始化粒子群及参数设置，计算每个粒子的适应度函数，根据pareto原则取舍种群并储存到外部存储库。

step2.2：令起始位置为个体最优，初始速度为0，计算pbest。

step2.3：根据2.1的方法计算外部存储库中的非劣解的拥挤度，选择gbest。

step2.4：更新粒子的速度、位置信息和适应度函数，更新外部存储库。

step2.5：检查是否到达最大迭代次数，若满足，则返回最优路径和适应度，否则转至step2.2。

step3：对种群进行交叉、选择和变异等操作，产生新一代种群。

step4： 种群更新。

step5： 检查终止迭代规则， 若满足，则输出结果， 否则转至step2。

综上所述，step2.1—step2.5为MOPSO的算法流程，其他为GA的算法流程。算法流程图如图4所示。

2.3 编码方式

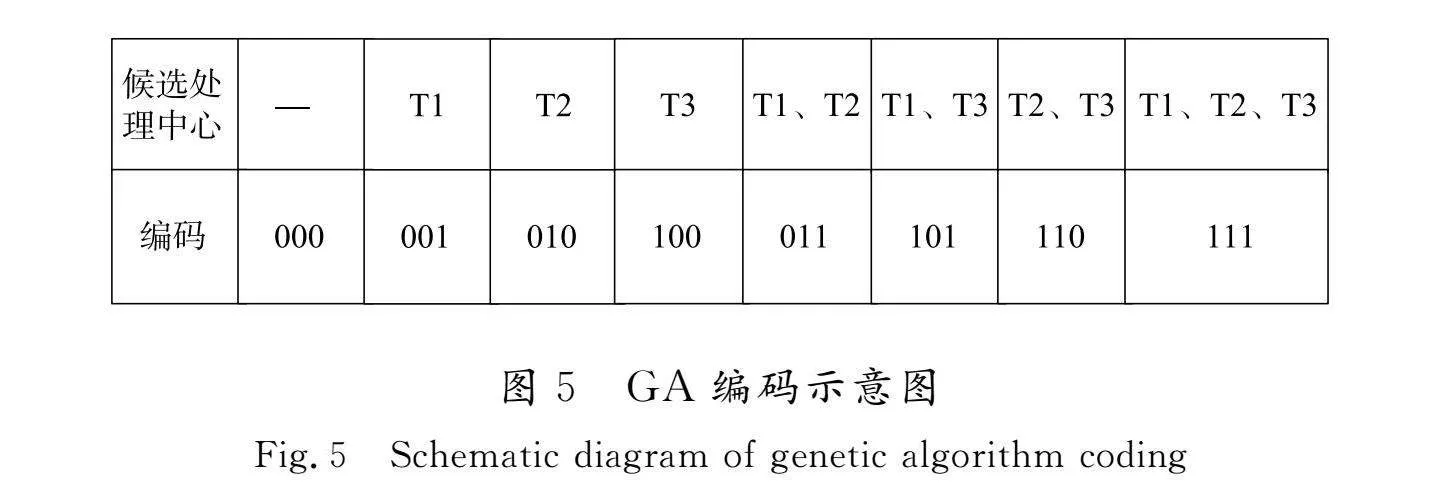
GA部分采用二进制编码，将染色体表示为0和1的序列，并随机生成一组这样的序列作为初始种群。若某位置对应候选中心，则编码为1，否则为0。GA编码示意图如图5所示。

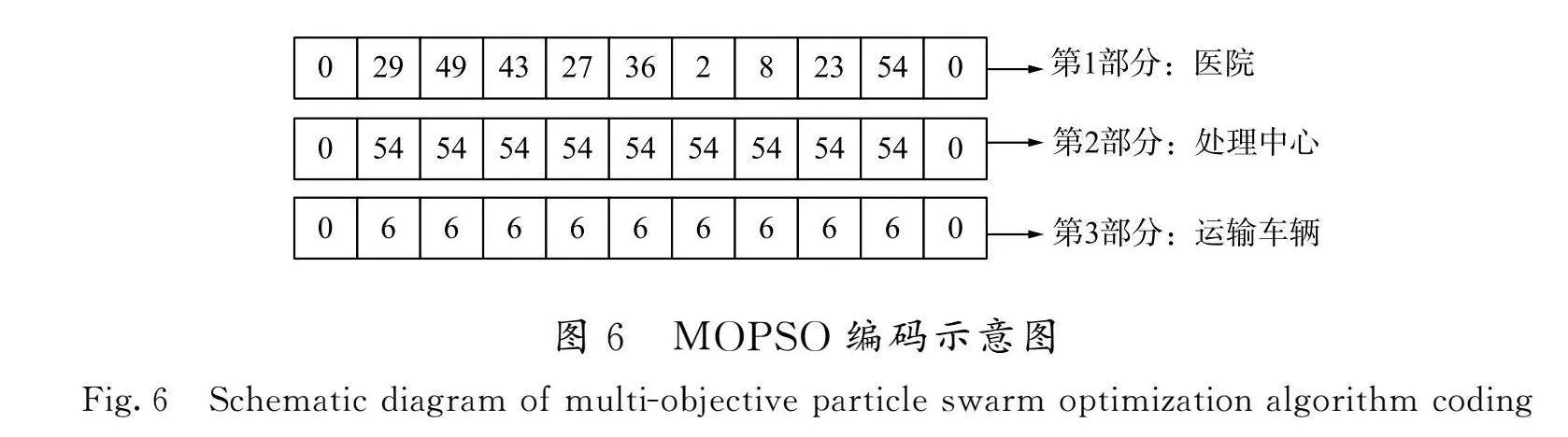
MOPSO通过自然数矩阵编码形成3×n矩阵，该三维矩阵代表一个配送方案，先根据医院配送线路选择处理站，再交由车辆完成配送。其编码包含医院配送路径、处理中心和运输车信息，如图6所示。

2.4 适应度函数

GA选取的适应度函数以最小化总成本为标准，涵盖了建设处理中心、运营处理中心及运输的各项成本。每个染色体代表一个选址方案，因此，个体x的适应度函数为

f（x）=1/C（x）。

MOPSO的适应度函数源于对多个目标函数的综合考虑，因此直接针对3个不同的目标函数进行优化。即，将这3个目标函数经过适

当的换算，统一到同一计量单位下，以cost_fitness定义。

2.5 遗传操作

1）选择 采用轮盘赌法从群体中挑选优秀个体作为父代进行遗传。假设群体有m个个体，个体i的适应度为f（xi），则个体i被选中遗传至下一代的概率与其适应度成正比，即

Pxi=f（xi）∑mif（xi）。

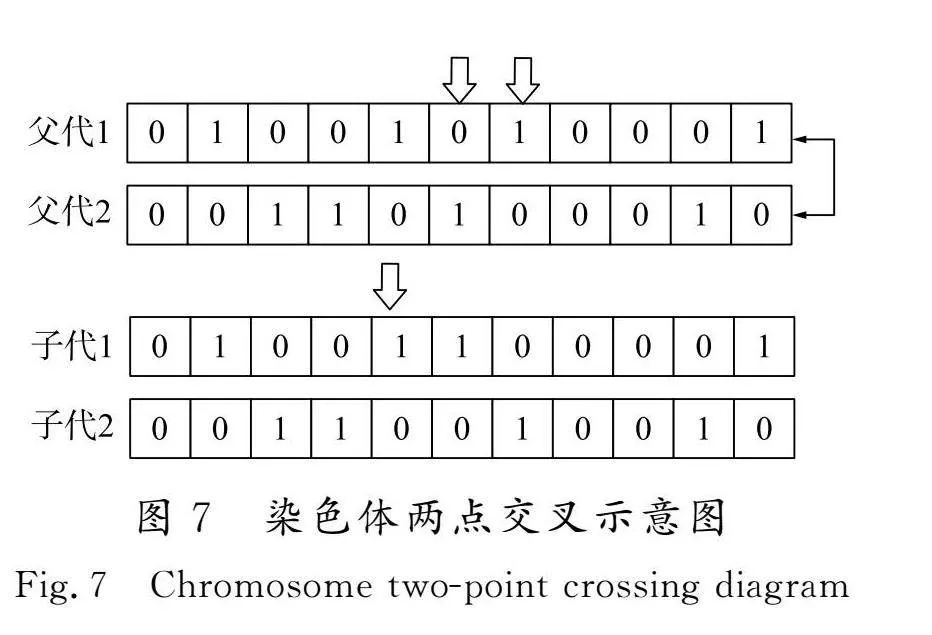
2）交叉 如图7所示，采用两点交叉方法，即随机选择2个染色体，并从中确定2个自然数n1和n2作为交叉点，随后交换这2个染色体在n1至n2之间的基因片段。

3）变异 如图8所示，随机从m个父本中选1个个体，若其变异概率在0.001～0.1之间，则对其前J个基因进行变异。变异过程就是随机选择2个基因位置并互换。

3 实例分析

3.1 数据来源

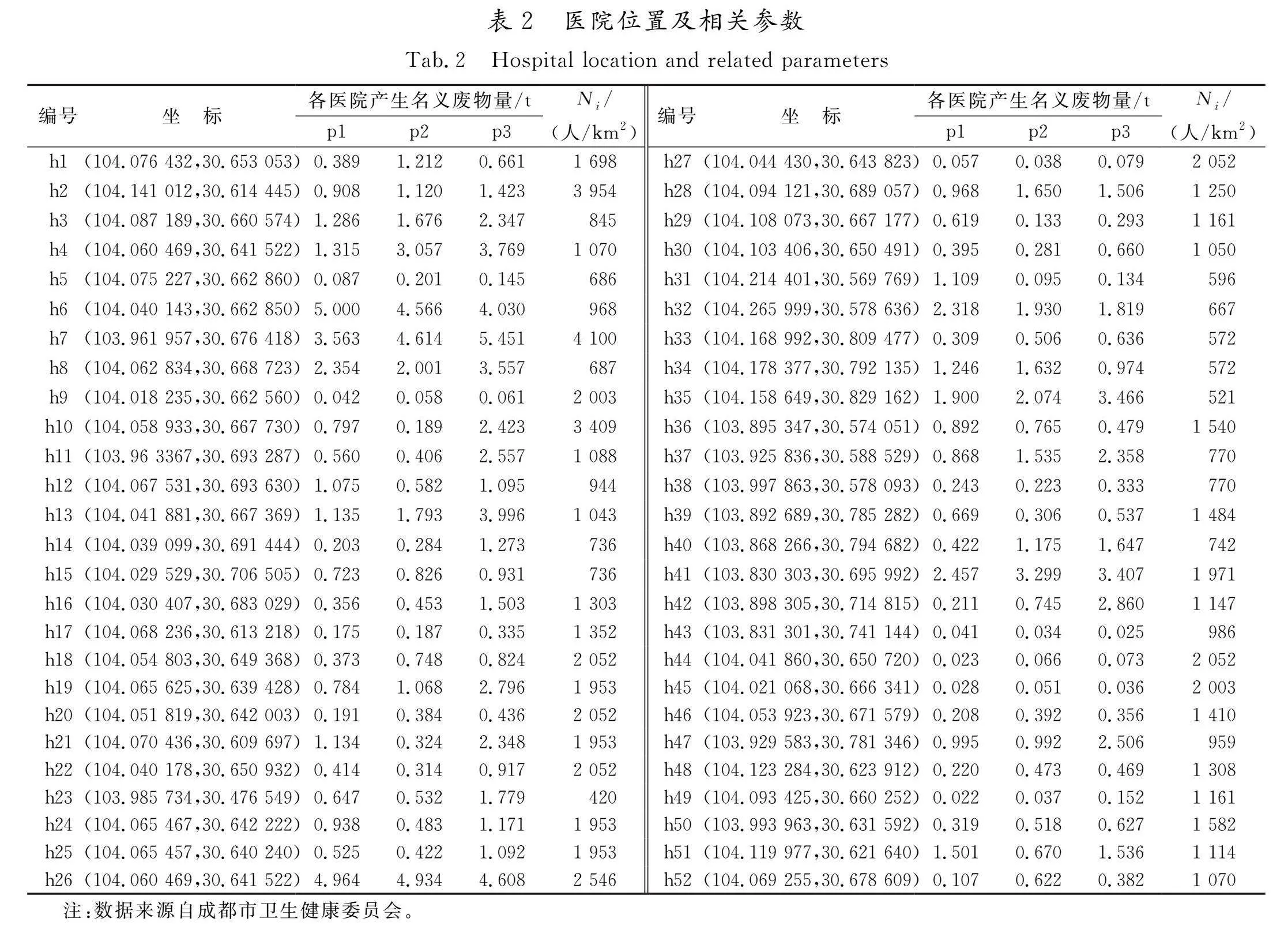
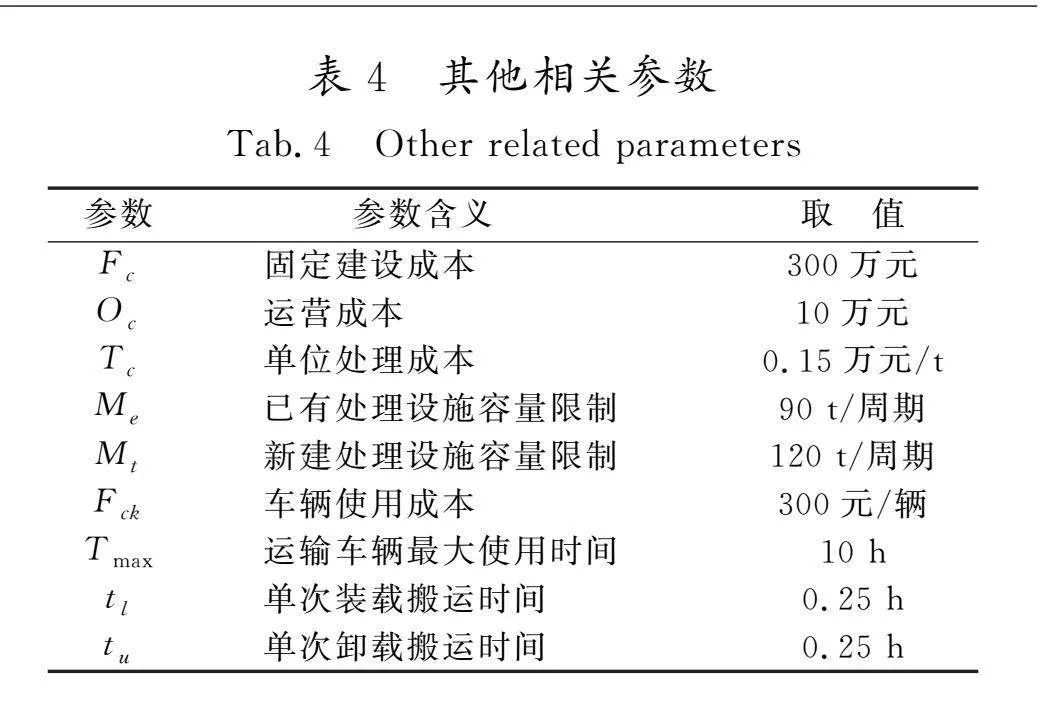
现以成都市医疗废物回收企业为例，其服务范围为该市所有的区，选取在其所负责区域内所有病床数在19张（含19张）以上的三甲和部分三乙医院作为配送点。回收网络中的所有配送点的位置坐标、医院所产生的名义废物量及人口密度如表2所示，该市已有医疗废物处理中心和候选医疗废物处理中心的位置坐标及人口密度见表3，其他相关参数见表4。另外，运输成本和节点i到节点j的人口密度由于数据量较大，本文不做展示。医疗废物7111eb4821267bbc49947cbdab7bc26e86d2af31a8c9716ad1227e4332bbcfb9运输过程中产生风险的概率为3.6×运输距离×10-7[21]，处理中心发生风险的概率为πr2×人口密度[22]，处理中心的感染半径设置为2 km[23]。

3.2 试验结果与分析

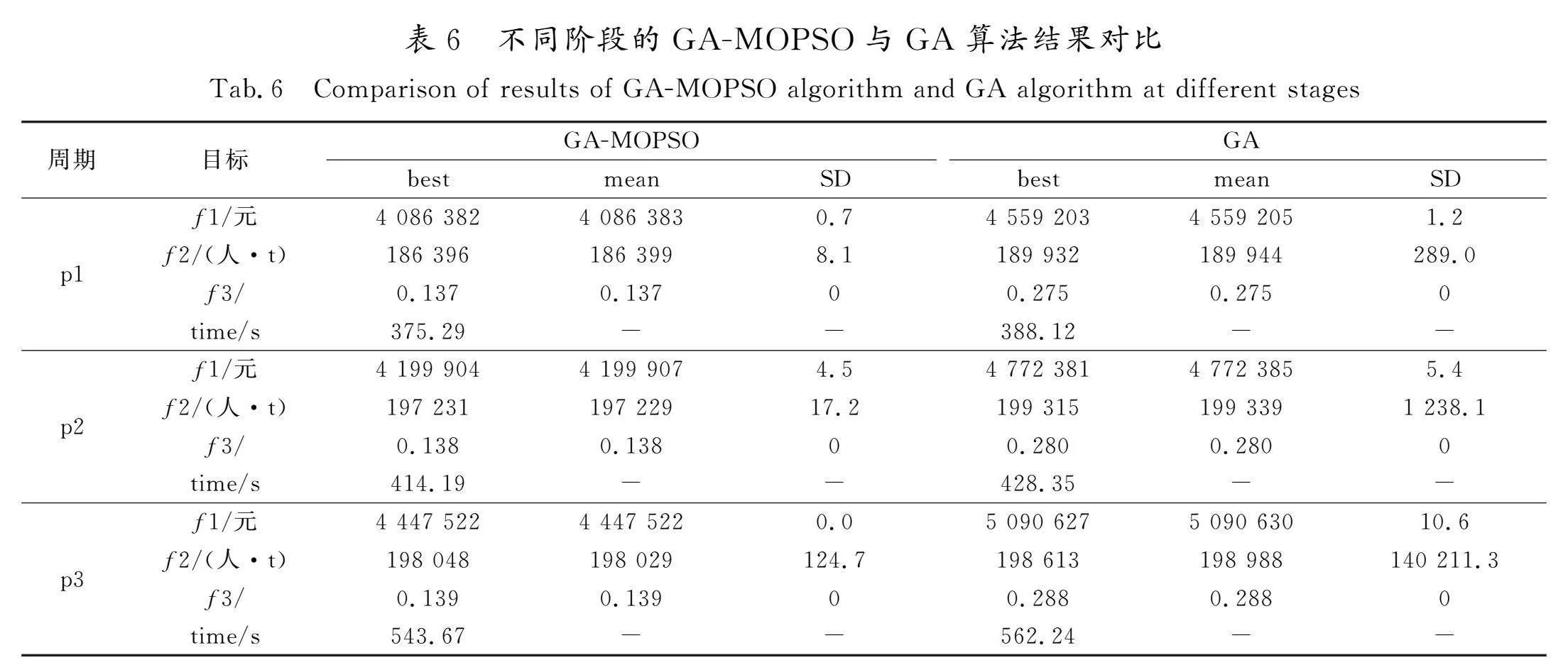
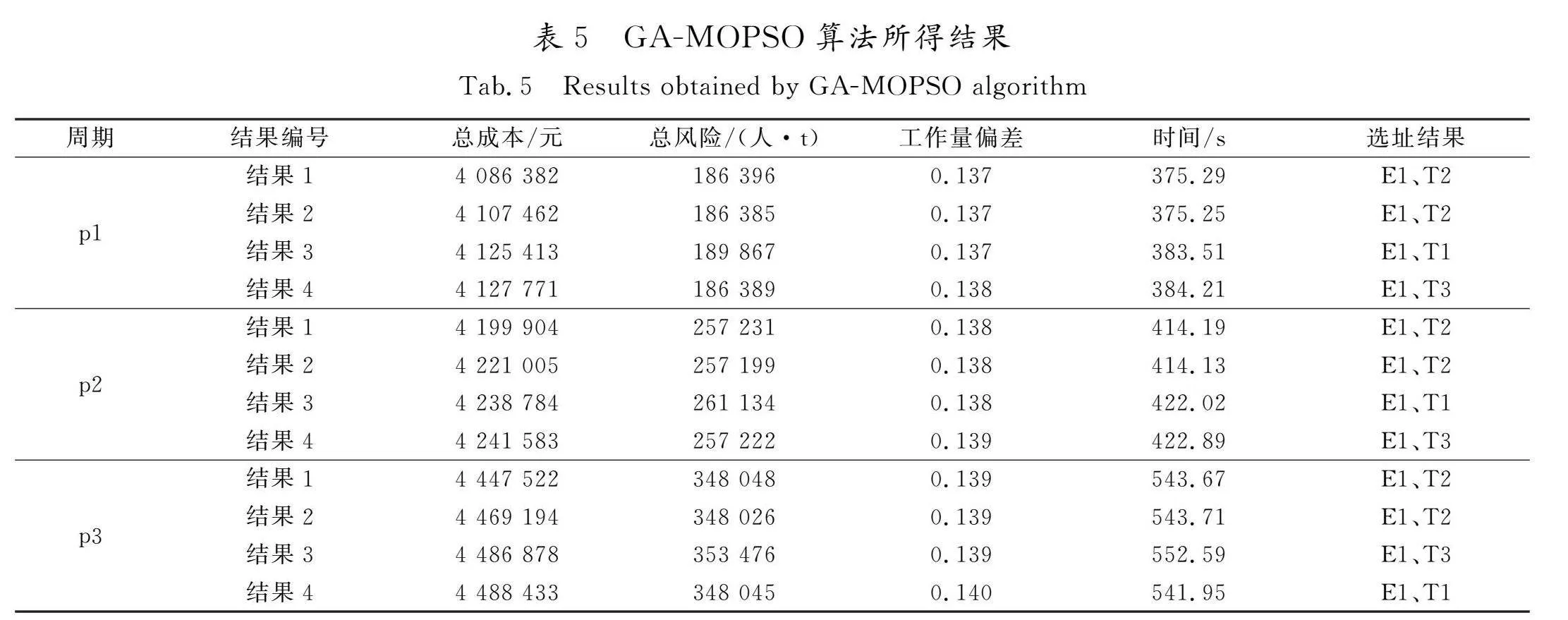
本文采用Python2022软件编写GA、MOPSO代码，所有试验都在Corei5/2.5 GHz/Windows11的计算环境下完成。GA参数设置如下：初始化种群pop_size=20，交叉概率cross_rate=0.8以及变异概率mutation_rate=0.1；MOPSO设pop_size=20，外部存储库repository=100，求解次数run_num=200。由于本文模型是多目标问题，求解选址问题时将多目标问题通过加权转化为单目标求解，其权重从大到小依次是成本（weight=0.6）、风险（weight=0.3）和满意度（weight=0.1）。另外，由于不确定参数的控制系数取值范围有所不同，为了所得结果更直观，将Γi、Γpi这2个控制系数归一化处理，控制系数变化范围为[0，10]。每周期经过20次独立运算得到运行结果可知，根据表5运行结果，T2为选址的最优结果。同时，为了比较本算法的有效性和稳定性，将路径优化阶段的MOPSO算法改成GA算法进行对比，2种算法的最优计算结果（best）、最优计算结果的平均值（mean）和标准差（SD）见表6。

由表6算法对比可知，GA-MOPSO所求解结果比GA算法有明显优势，比如p1周期内，GA-MOPSO所求总成本比GA低10.37%，总风险低1.86%，工作量偏差低50.18%，求解速度快3.31%。这说明，在医疗废物回收网络的场景中，GA-MOPSO具有更好的求解性能。相较于GA，GA-MOPSO不仅能够降低成本和风险，还能实现更合理的车辆分配路径。更重要的是，这种优势在不同周期内也得到了验证。从SD来看，GA-MOPSO在总成本和工作量偏差上的SD值普遍低于GA，表明GA-MOPSO在这些目标上产生的解更为稳定。对于总风险，尽管在某些周期中GA-MOPSO的SD值偏高，但相较于GA，GA-MOPSO仍然具有优越性。

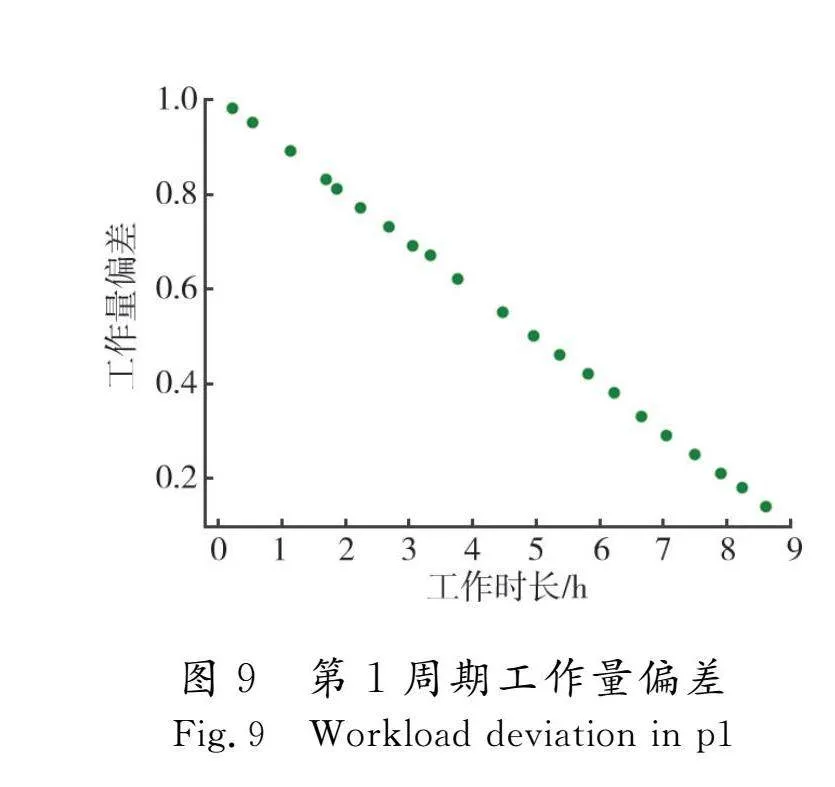
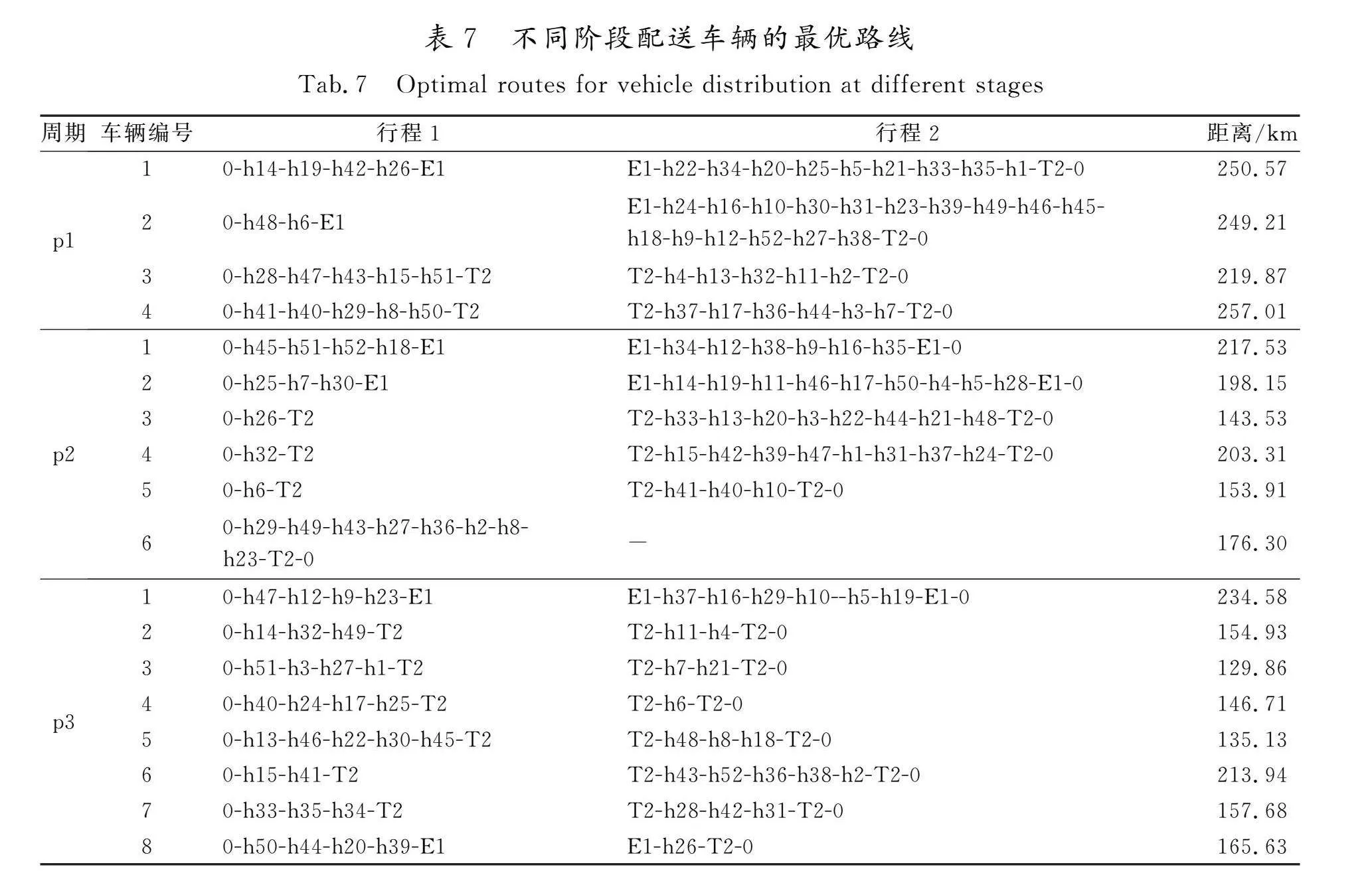
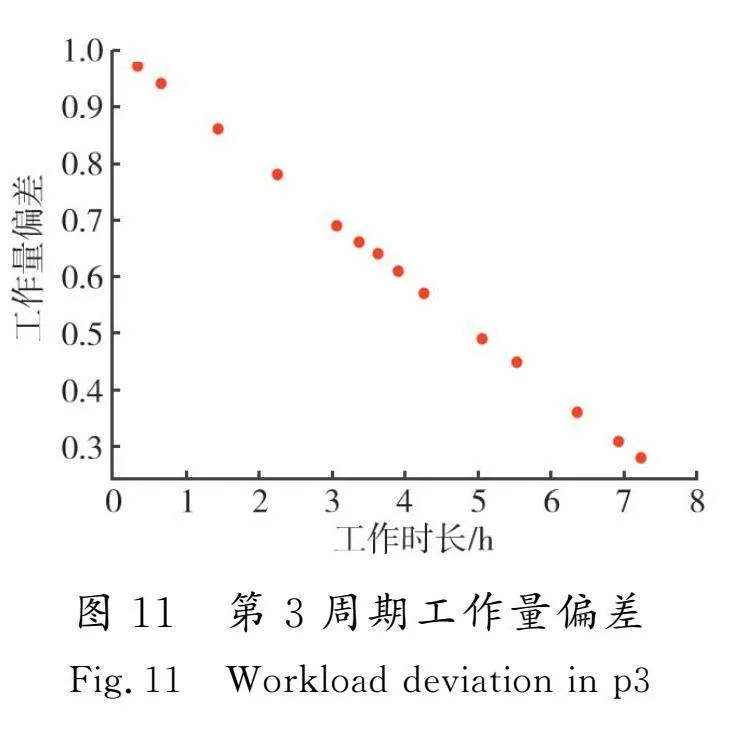
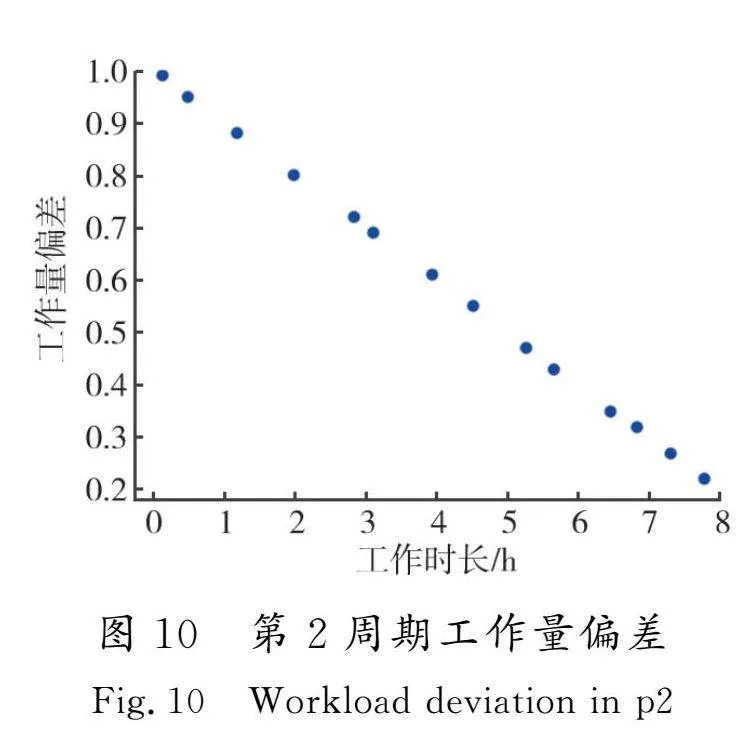
表7是GA-MOPSO所求解的不同阶段车辆的最优路线，可知每个阶段本算法所求的候选点均为T2，说明2种算法对于选址成本基本相同，因此导致2种算法所求结果大相径庭的便是配送路径，从而证明本文算法在路径优化方面更具优势。图9—图11是不同周期内工作量偏差随工作时间变化的结果，由图可知随着工作时间的减少，工作量偏差逐步增大，说明各时间段的车辆总服务时间得到平衡，员工满意度有所上升。

3.3 敏感性分析

为了研究鲁棒优化处理不确定信息的性能及效果，对模型中运输成本、医疗废物量对目标函数的影响进行分析，即对不确定参数的控制系数Γi、Γpi和车辆最长行驶时间Tmax进行敏感性分析。

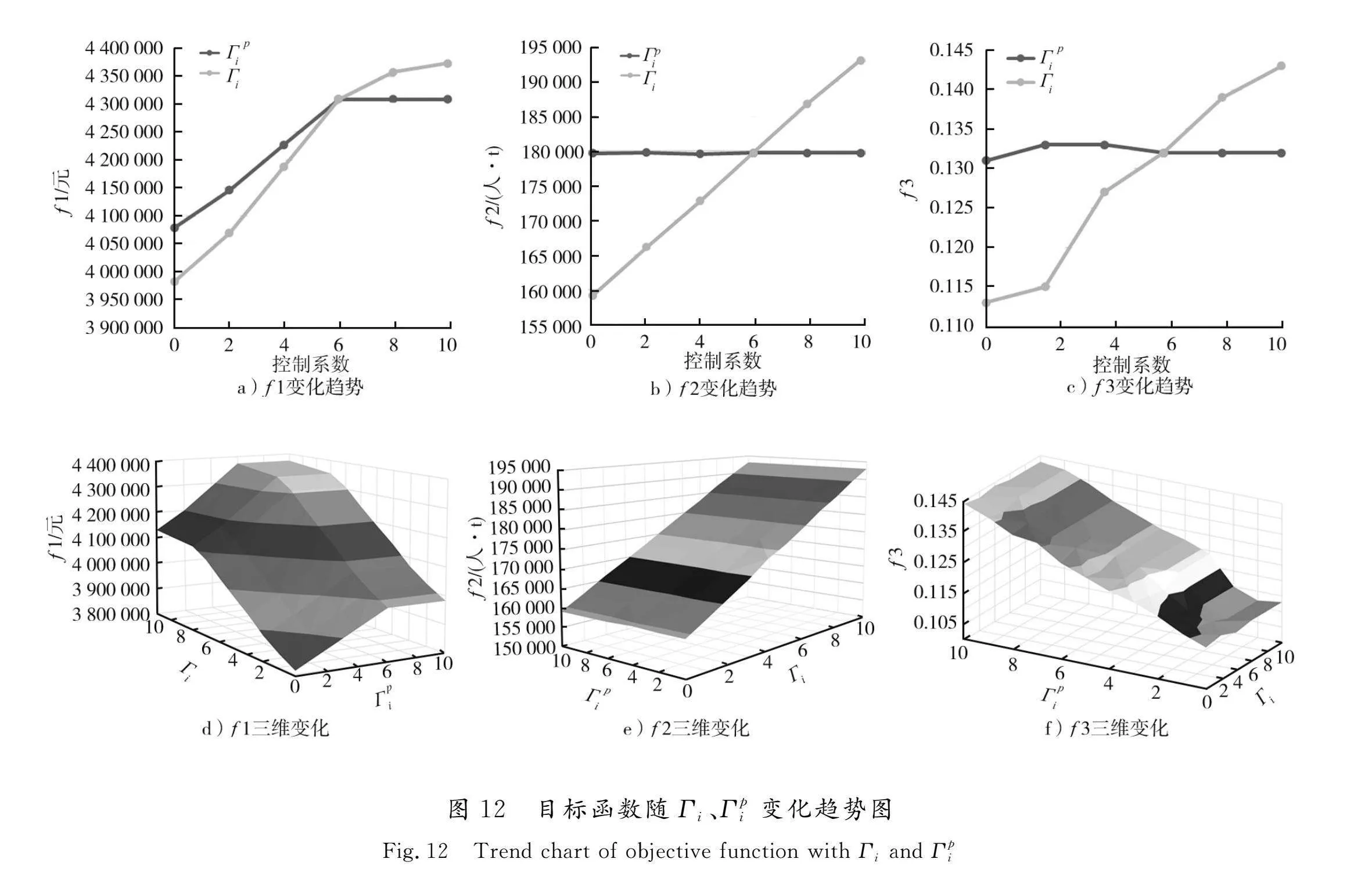
当Γi=Γpi=0时，鲁棒模型为名义模型，即为名义医疗废物量和名义运输成本下的线性规划模型。图12为Γi、Γpi在不同组合下对目标函数的影响，研究的是单一不确定参数变化相应的成本、风险和工作量偏差会如何变化。图12 a）—c）为运输成本或医疗废物产生量不确定时，总成本随着控制系数Γi、Γpi的变化趋势图，图12 d）—f）则是相应的三维变化曲面图。由图12 a）可以看出，随着Γi、Γpi的增加，总成本均呈上涨的趋势，当Γi≤6时，总成本增幅较为明显，当Γi≥6时，上涨的趋势有所下降。除此之外，无论Γi如何变化，Γi变化导致的总成本明显高于Γpi变化导致的总成本，说明医疗废物量的不确定性比运输成本的不确定性对总成本的影响更大。同理从图12 d）也可看出，相较于Γpi、Γi变化更能影响总成本。这是因为单位运输成本仅存在于成本目标函数，而医疗废物量的多少不仅影响成本、风险和工作量偏差，还会影响候选点的容量，因而影响候选点的位置选择。

图12 b）、e）是控制系数Γi、Γpi对总风险的影响，由图可知，随着Γi的增加，总风险单调递增，且增加的幅度明显。而随着Γpi增加，总风险无明显变化，说明运输成本的不确定性并不会对风险造成明显影响，仅有医疗废物量的不确定性能引起总风险的明显变化。图12 c）、f）展示了控制系数Γi或Γpi变化对工作量偏差的影响，由图不难看出单位运输成本不会影响工作量偏差，而Γi却能引起工作量偏差变化，Γi越大工作量偏差也越大，说明Γi增大各时间段的车辆总服务时间的平衡状态愈加恶化。其实Γi能对3个目标函数产生明显影响的根本原因还是在于废物量多少能间接影响候选点的位置问题。

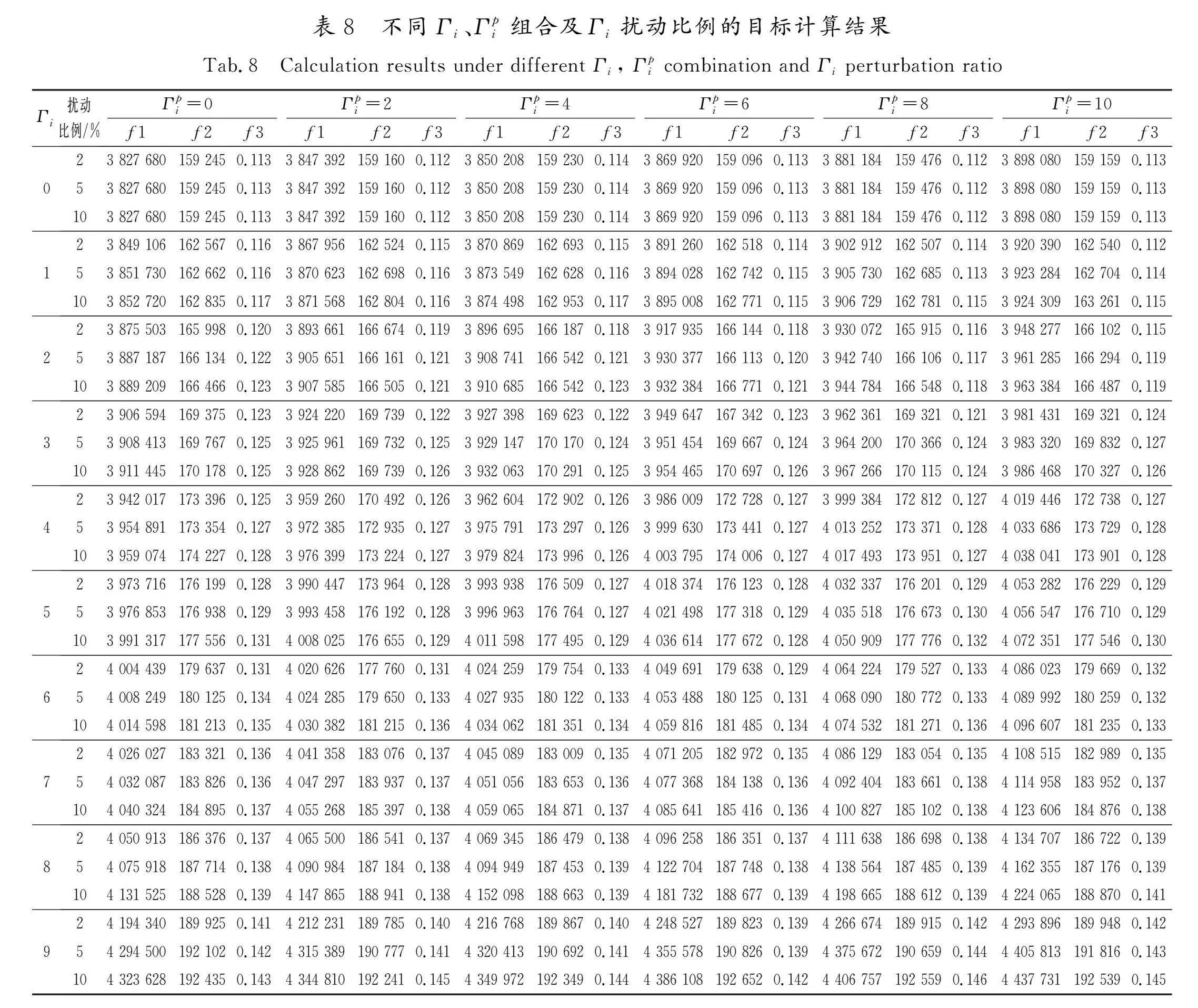
表8为控制系数Γi、Γpi在不同组合下当医疗废物量发生扰动（2%、5%和10%）的计算结果，单位运输成本的扰动比例为5%。由表8可知，当Γi、Γpi增加时，单位运输成本和医疗废物量的不确定性增加，鲁棒模型的保守性增强，最优总成本增大。另外，由医疗废物量的扰动比例可知，相同扰动比例下目标函数随着Γi、Γpi增加而增加；当不同Γi、Γpi组合时，目标函数亦随着扰动比例增大而增大，说明不确定性增加，风险也就越大，因此决策者可以根据自己对风险的喜好程度选择Γi和Γpi的组合方式，以使所求得的结果最优。

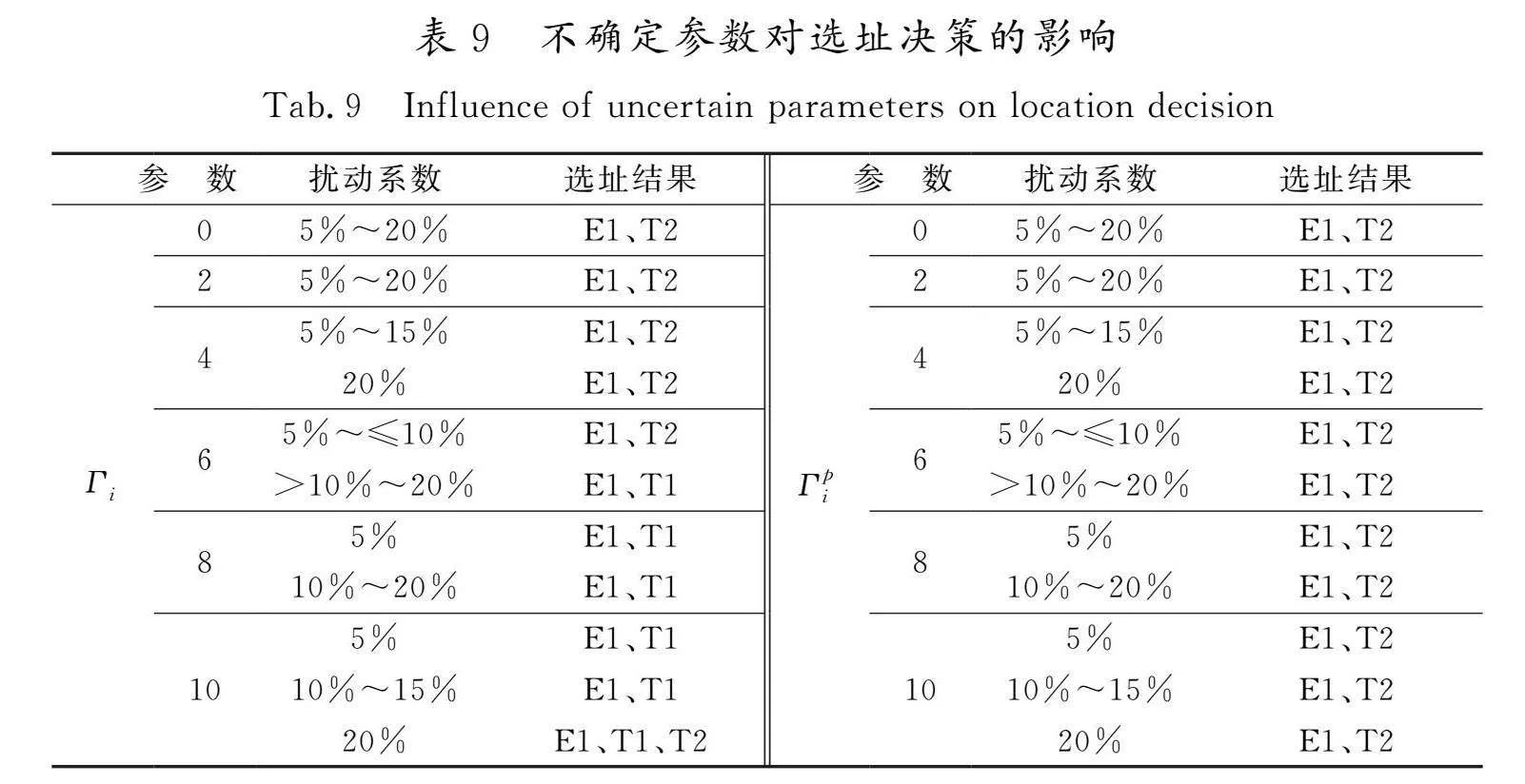
由表9可知，随着Γi的不断增大，废物量的不确定性增大，迫使医疗废物回收网络开放更多的候选处理点，而单位运输成本对选址决策无影响。

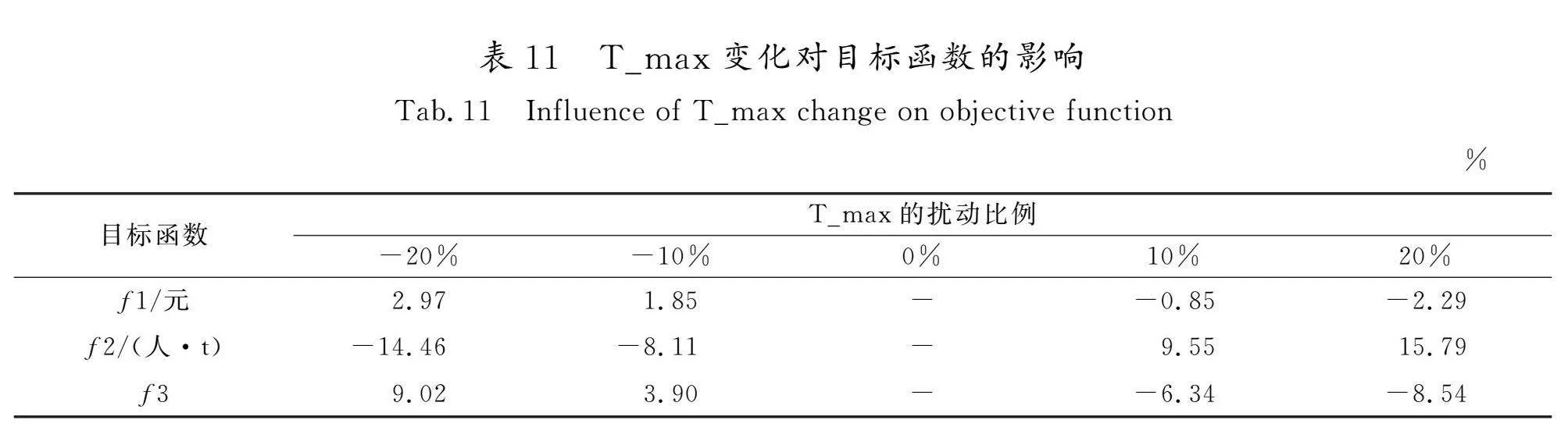
表10和表11为不同扰动比例下的T_max对目标函数的影响。由表10可以看出，随着T_max的变化，3个目标函数在不同方向上发生了变化。首先是总目标和工作量偏差随着T_max的增大而减小。由于车辆最大使用时间增加，车辆能在1个周期obvv1ClXiPyuqoCL4h6ZpQ==内完成更多的回收服务，因此车辆使用成本降低。同时，这种变化也导致了工作量的偏差。由于车辆使用率提高和运往处理站的运往次数减少，车辆在各时间段的总服务时间达到平衡。而总风险随着T_max的增大而增大，是由于车辆在更多的使用时间内运输了较以往更多的医疗废物所致。表11为目标函数在T_max的不同扰动比例下变化的百分比。由此可知，增幅最大的是总风险，增长了15.79%，其余2个目标的变化均小于目标二，说明参数T_max对总风险有较大影响。综上所述，增加参数T_max可以减少成本和工作量偏差，但是会导致总风险增加。根据以上结果，决策者可以找到最合适的参数值以完成回收网络的构建和分配。

4 结 语

在医疗废物回收工作的不确定环境背景下，考虑回收量和运输成本2个不确定因素，从成本、风险以及工作量偏差等3个方面，构建了不确定信息环境下多周期多目标的处理中心选址和路径优化模型，以研究医疗废物处理设施选址和流量分配问题。由于模型含有2个不确定参数，导致所构建的模型不具有明确意义且约束条件不清晰。利用鲁棒优化方法，转化成可求解的混合线性整数规划模型，并将引入拥挤距离和非支配排序思想的MOPSO算法与GA算法相结合，提出GA-MOPSO算法。以成都市的实际数据作为算例，从应用层面验证了该算法的可靠性。对重要参数进行的敏感性分析表明，相较于运输成本的不确定性，医疗废物量的不确定性更能引起目标函数的明显变化。除此之外，车辆的最大使用时间也会引起总成本和工作量偏差变化明显。因此，决策者可以根据对风险的偏好选择不确定参数的组合以及T_max，以获得最优的医疗废物回收网络优化方案。

本文算法在求解大规模算例时耗时较长，且只采用了MOPSO和GA进行求解。未来拟选择非支配排序算法（NSGA-Ⅱ）或其他多目标算法进行研究。同时，本文没有考虑医疗废物分类问题，而现实中已经有医院提出医疗废物分类处理，这也是本文进一步的研究方向。

参考文献/References：

[1] World

Health Organization.Safe Management of Wastes from Health-Care Activities：A Summary[R].World Health Organization，2017.

[2] BEIKI H，SEYEDHOSSEINI S M，GHEZAVATI V R，et al.Multi-objective optimization of multi-vehicle relief logistics considering satisfaction levels under uncertainty[J].International Journal of Engineering，2020，33（5）：814-824.

[3] SAEIDI M Z，TAVAKKOLI M R，NAVABAKHSH M，et al.A bi-level and robust optimization-based framework for a hazardous waste management problem：A real-world application[J].Journal of Cleaner Production，2020.DOI：10.1016/j.jclepro.2019.119830.

[4] BABAEE T E，GOLI A，PAHLEVAN M，et al.A robust bi-objective multi-trip periodic capacitated arc routing problem for urban waste collection using a multi-objective invasive weed optimization[J].Waste Management & Research，2019，37（11）：1089-1101.

[5] JONEGHANI N M，ZARRINPOOR N，EGHTESADIFARD M.A mathematical model for designing a network of sustainable medical waste management under uncertainty[J].Computers & Industrial Engineering，2022.DOI：10.1016/j.cie.2022.108372.

[6] 蒲松，夏嫦.基于二阶段随机规划的城市医疗废弃物回收网络设计[J].中国管理科学，2021，29（5）：166-172.

PU Song，XIA Chang.A two-stage stochastic programming approach for urban medical waste recycling network design[J].Chinese Journal of Management Science，2021，29（5）：166-172.

[7] YU Hao，SUN Xu，SOLVANG W D，et al.A stochastic network design problem for hazardous waste management[J].Journal of Cleaner Production，2020.DOI：10.1016/j.jclepro.2020.123566.

[8] ZHAO Jiahong，WU Biaohua，KE G Y.A bi-objective robust optimization approach for the management of infectious wastes with demand uncertainty during a pandemic[J].Journal of Cleane_{498c168219c276167d002b097597fcfd92466c387e698661297f9da86e9518ff}r ProductionLQ6G3w+w5tC9nHFq1QFzwnAmdADpZLhlllMkQCX4iOs=，2021.DOI：10.1016/j.jclepro.2021.127922.

[9] KARGAR S，PAYDAR M M，SAFAEI A S.A reverse supply chain for medical waste：A case study in Babol healthcare sector[J].Waste Management，2020，113：197-209.

[10]MISHRA A R，RANI P，MARDANI A，et al.Healthcare evaluation in hazardous waste recycling using novel interval-valued intuitionistic fuzzy information based on complex proportional assessment method[J].Computers & Industrial Engineering，2020.DOI：10.1016/j.cie.2019.106140.

[11]GHOUSHCHI S J，BONAB S R，GHIACI A M，et al.Landfill site selection for medical waste using an integrated SWARA-WASPAS framework based on spherical fuzzy set[J].Sustainability，2021.DOI：10.3390/su121413950.

[12]MI Xiangjun，TIAN Ye，KANG Bingyi.A hybrid multi-criteria decision making approach for assessing health-care waste management technologies based on soft likelihood function and D-numbers[J].Applied Intelligence，2021，51（10）：6708-6727.

[13]YU Hao，SUN Xu，SOLVANG W D，et al.Reverse logistics network design for effective management of medical waste in epidemic outbreaks：Insights from the coronavirus disease 2019 （COVID-19） outbreak in Wuhan （China）[J].International Journal of Environmental Research and Public Health，2020.DOI：10.3390/ijerph17051770.

[14]TIRKOLAEE E B，ABBASIAN P，WEBER G W.Sustainable fuzzy multi-trip location-routing problem for medical waste management during the COVID-19 outbreak[J].Science of the Total Environment，2021.DOI：10.1016/j.scitotenv.2020.143607.

[15]李欣，陈希.疫情暴发流行期传染性医疗废弃物的多目标三级网络优化研究[J].运筹与管理，2023，32（6）：75-81.

LI Xin，CHEN Xi.Multi-objective three-level network optimization of infectious medical waste during the epidemic period[J].Operations Research and Management Science，2023，32（6）：75-81.

[16]鲍秀麟，张惠珍，马良，等.考虑公众风险的多目标医疗废物选址路径问题及樽海鞘算法求解[J].计算机应用研究，2023，40（3）：710-716.

BAO Xiulin，ZHANG Huizhen，MA Liang，et al.Salp swarm algorithm for multi-objective medical waste location-routing problem considering public risk[J].Application Research of Computers，2023，40（3）：710-716.

[17]KUMAR S K.PRIYANKA H.Bio-medical wastes management in davanagere city[J].International Journal of Civil and Structural Engineering Research，2015，3（1）：255-260.

[18]SOUMIA I，MICHEL G，POTVIN J Y.Vehicle dispatching with time-dependent travel times[J].European Journal of Operation Research，2003，144（2）：379-396.

[19]孙华丽，李泽平，马腾.道路修复联合应急设施选址-路径鲁棒优化研究[J].系统工程理论与实践，2023，43（9）：2701-2713.

SUN Huali，LI Zeping，MA Teng.Robust optimization of joint road restoration and emergency location-routing[J].Systems EngiElGSFj8yJ8gBCVgQigHd4UsgFC9HNgFaKcDuMZkIjns=neering-Theory & Practice，2023，43（9）：2701-2713.

[20]关菲，张强.模糊多目标物流配送中心选址模型及其求解算法[J].中国管理科学，2013，21（sup1）：57-62.

GUAN Fei，ZHANG Qiang.A fuzzy multi-objective logistics distribution center location model and its solution algorithm[J].Chinese Journal of Management Science，2013，21（sup1）：57-62.

[21]ZHAO Jun，HUANG Lixia，LEE D H，et al.Improved approaches to the network design problem in regional hazardous waste management systems[J].Transportation Research Part E：Logistics and Transportation Review，2016，88：52-75.

[22]ZHAO Jun，HUANG Lixiang.Multi-period network design problem in regional hazardous waste management systems[J].International Journal of Environmental Research and Public Health，2019.DOI：10.3390/ijerph16112042.

[23]HE Zhenggang，LI Qing，FANG Jie.The solutions and recommendations for logistics problems in the collection of medical waste in China[J].Procedia Environmental Sciences，2016，31：447-456.