例谈求解圆中阴影部分面积的方法

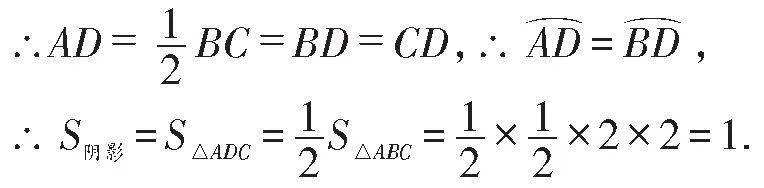
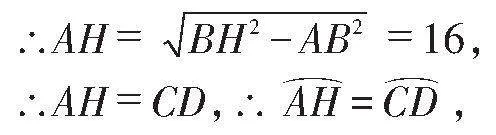
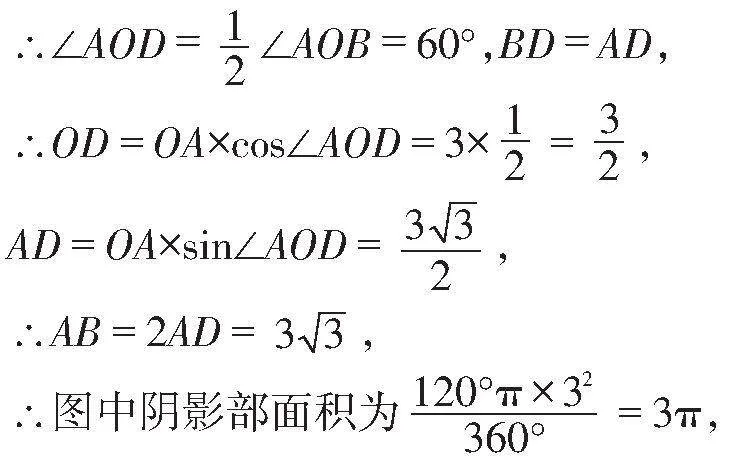
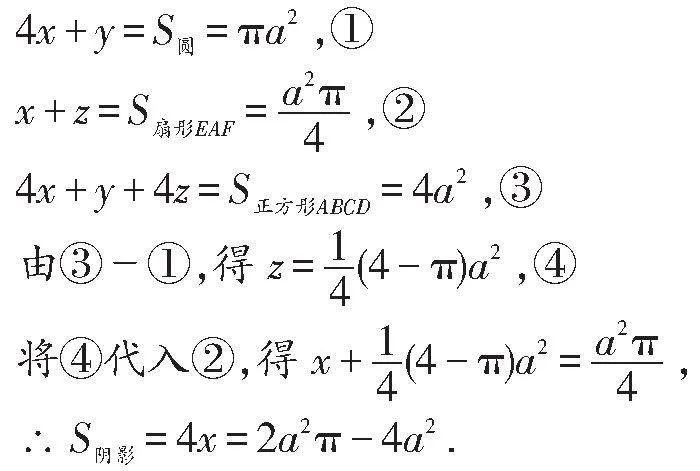
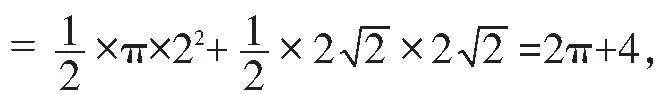
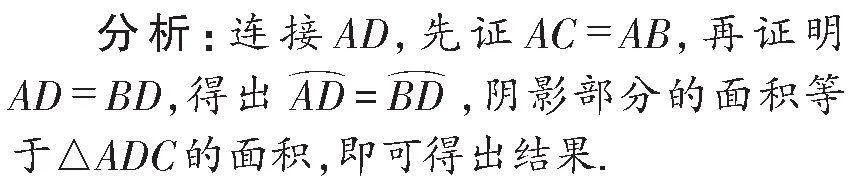
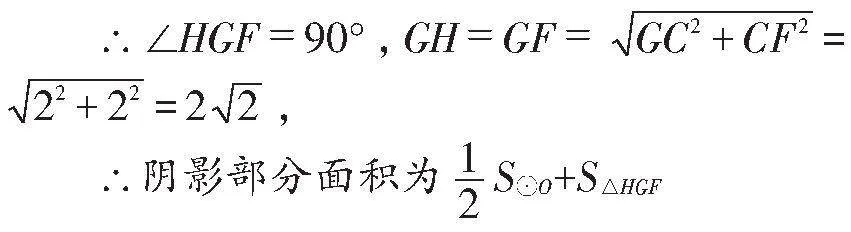
求圆中阴影部分的面积是计算题的一种重要类型.此类问题中阴影部分的图形一般是不规则图形，同学们在求解时，要注意观察和分析图形，学会分解和组合图形，将图形的阴影部分通过割补、和差变换、等积代换等方式转化成扇形、三角形、弓形等规则图形，然后再运用相应面积公式计算.

一、公式法

当所求阴影部分的面积是规则图形，且求解所需条件，如线段、角度等都容易求得时，可以直接用圆形、扇形或多边形的面积公式进行求解.

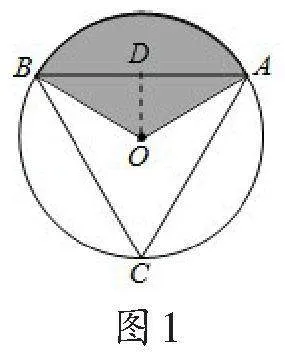
例1如图1，△ABC是⊙O的内接正三角形，⊙O的半径为3，则图中阴影部分的面积是________.

分析：作OD⊥AB于D，根据等边三角形的性质得到∠ACB=60°，根据圆周角定理求出∠AOB，解直角三角形求出OD、AD，再根据扇形面积公式、三角形面积公式计算出结果.

解：作OD⊥AB于D，如图1，

∵△ABC为等边三角形，∴∠ACB=60°，

∴∠AOB=2∠ACB=120°，

∵OA=OB，OD⊥AB，

故答案为3π.

二、和差法

当阴影部分是不规则图形时，可将不规则图形看成是几个规则图形的组合，将阴影部分面积转化为几个规则图形面积的和差来进行求解.通过将规则图形的面积相加或相减得到阴影部分的面积.

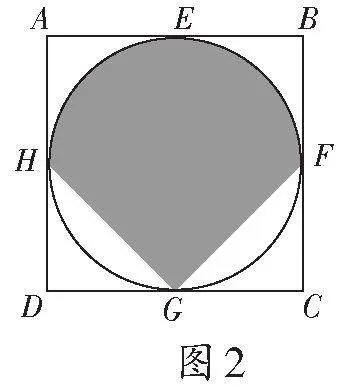
例2如图2，边长为4的正方形ABCD外切于圆。，则阴影部分的面积为（）.

A.2π-4 B.2π+4 C.15 D.14

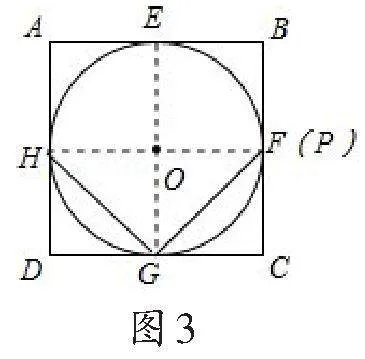
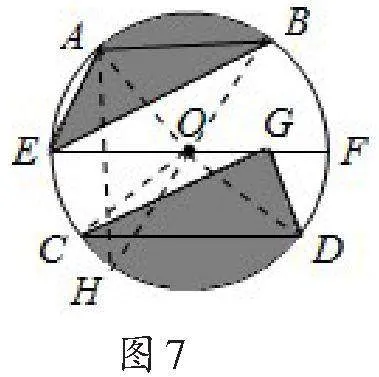
解：如图3，连接HO，延长HO交BC于点P，

∵正方形ABCD外切于⊙O，

∴∠A=∠B=∠AHP=90°，

∴四边形AHPB为矩形，

∴∠OPB=90°，

又∠OFB=90°，∴点P与点F重合

∴HF为⊙O的直径，同理EG为⊙O的直径，

由∠D=∠OGD=∠OHD=90°且OH=OG知，四边形GOHD为正方形，

同理，四边形OGCF、四边形OFBE、四边形OEAH均为正方形，

∴DH=DG=GC=CF=2，

∠HGO=∠FGO=45°，

故选B项.

说明：通过添加适当的辅助线，可以把阴影部分的面积转化为半圆面积和三角形面积之和来求解.

三、割补法

若由于图形不规则造成直接求阴影部分面积较为困难，可对图形进行合理的分割或填补，将不规则的多边形或有圆弧的图形整合成一个规则图形，然后再结合图形的面积公式，逐一求解.

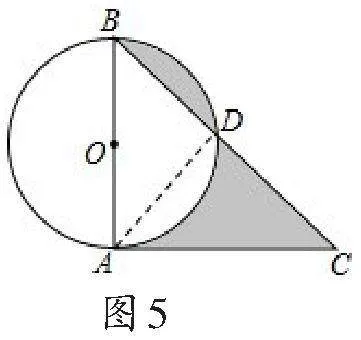
例3如图4，在⊙O中，直径AB=2，CA切⊙O于A，BC交⊙O于D，若∠C=45°，则阴影部分的面积为_______.

解：连接AD，如图5所示：

∵CA是⊙O的切线，∴AB⊥AC，

∴∠BAC=90°，

∵∠C=45°，∴∠B=90°-45°=45°，

∴AC=AB=2，

∵AB是直径，∴∠ADB=90°，

即AD⊥BC，∴CD=BD，

故答案为1.

说明：证明阴影部分的面积等于△ADC的面积是解答本题的关键.通过添加适当的辅助线，可以把阴影部分的面积分割拼凑为三角形的面积进行计算.利用割补法解题时需注意两点：一是避免分割过于分散；二是割补过程需确保面积相等.

四、等积代换法

等积代换法就是对所求图形进行等面积变化，将不规则图形的面积转化为与它等面积的规则图形来进行计算，如利用“同底等高的两个三角形的面积相等”以及“平移、旋转不改变图形的形状与大小”等进行等面积转换，再结合面积公式求解.

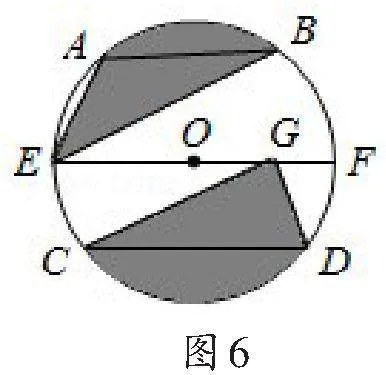
例4如图6，⊙O的直径EF为20cm，弦AB，CD位于直径EF的异侧，长度分别为12cm，16cm，AB∥EF∥CD，点G在线段EF上，则图中阴影部分面积之和为_______cm2.

解：连接AO，BO，延长BO交⊙O于H，连接AH，如图7，则∠HAB=90°，

∵AB=12，BH=EF=20，

连接OC，OD，则S扇形AOH=S扇形COD，

∵CD∥EF，∴S△OCD=S△CDG，

∴S阴影DCG=S扇形COD，∴S阴影DGC=S扇形AOH，

同理，S△ABE=S△AOB，S阴影ABE=S扇形AOB

故答案为50π.

说明：通过添加适当的辅助线，利用三角形全等、同底等高的三角形面积相等，可以把不规则的阴影部分的面积转化为扇形的面积来计算.

五、方程法

当图形的构造较为复杂，用一般方法求解阴影图形的面积比较麻烦时，可以通过设元，建立方程组求解.有些图形的局部具有等面积和对称的性质，这时可把阴影部分面积、整体面积以及非阴影部分面积的关系用方程组表示出来，通过解方程组求出阴影图形的面积.

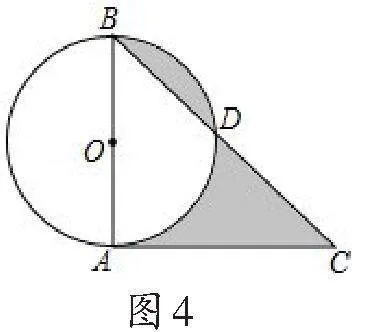
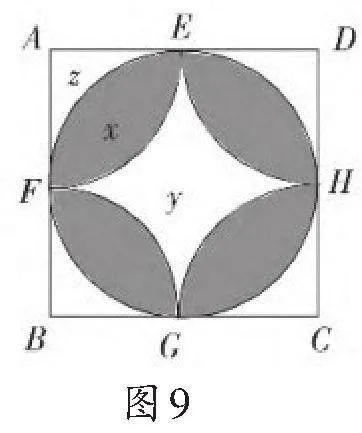
例5如图8，正方形ABCD中，有一个以正方形的中心为圆心，以一边长为直径的圆， 分别以A，B，C，D为圆心，以边长的一半为半径画四条弧.若正方形边长为2a，求所围成的阴影部分的面积.

分析：图中含有形状不同的三类图形，分别设为x、y和z，由图形特征知4个x和1个y组成一个圆，一个x和z组成一个扇形，而四个x、4个z和1个y组成一个正方形.

解：设图9中一个月形面积为x，中间空白部分面积为y，圆外四个空白中的一个空白部分面积为z，则有

说明：本题考查了圆、扇形及正方形的面积等知识.当图形的构造较复杂，用整合、变换的方法难以奏效时，可以另辟蹊径，利用方程组求解.

综上，通过分析与圆有关阴影部分面积问题的五种解法，可为解答阴影部分面积问题提供一些思路，同时也可提升解题效率.