怎样利用一元二次方程解答三类实际问题

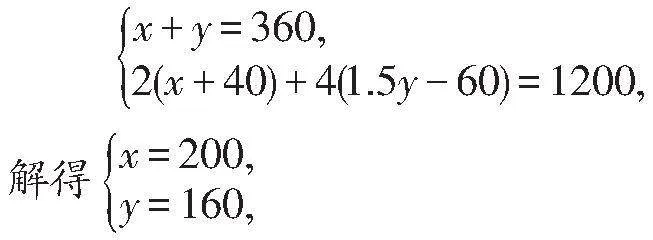
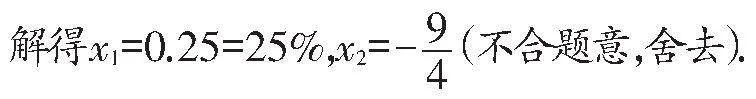
一元二次方程是只含有一个未知数，且未知数的最高次数为2的方程，一般形式为ax2+bx+c=0，其中a、b、c是常数，且a≠0.通过建立一元二次方程，可以解答多种实际问题，如增长率问题、销售利润问题等.下面举例予以说明.

一、增长率问题

有许多实际问题都是增长率问题，如求产品销量、生产产量、农作物的种植量等.运用一元二次方程解答增长率问题需要理清原有量、增长后的量、增长率，第1次增长后的量=原有量×（1+增长率），第2次增长后的量=原有量×（1+增长率）2.当然有增长率，就有降低率，若两次均降低，则第2次降低后的量=原有量×（1-降低率）2.运用这一公式，设元建立一元二次方程即可解题.

例12023年10月26日，神舟十七号发射升空与空间站构成三船三舱构型.某纪念品商店为满足航空航天爱好者的需求，特推出了“中国空间站”模型.已知该模型每件成本40元，当商品售价为70元时，十月售出256件，十一月、十二月销量持续走高，十二月售出400件.求十一月、十二月这两个月的月平均增长率.

分析：由题意可得，十月份的销售量为： 256件；设十月份到十二月份销售额的月平均增长率为x，则十一月份的销售量为：256（1+x）件；十二月份的销售量为：256（1+x）（1+x）

件，又知十二月售出400件，由此等量关系列出方程求出x的值，即求出了平均增长率.

解：设十一月、十二月这两个月的月平均增长率为x，则十一月的销售量为256（1+x）件，十二月的销售量为256（1+x）2件.

根据题意可得：256（1+x）2=400，

答：十一月、十二月这两个月的月平均增长率为25%.

点评：本题要求月平均增长率，解题的关键在于准确理解题意，提取相关的量，根据增长率公式列出方程.值得注意的是一元二次方程有两个解，要根据实际意义进行取舍.

二、传播问题

传播问题涉及多种类型，如计算机网络传播、疾病传播、经济数据波动等.利用一元二次方程解答这类传播问题，首先需要关注起始值、新增数量，并找出数量变化规律，通常用到数量关系式为第一轮传播后的量=传播前的量×（1+传播速度），第二轮传播后的量=第一轮传播后的量×（1+传播速度）=传播前的量×（1+传播速度）2，根据这一关系式设元、列方程求解.

例2春季流感严重，学校有2个人患了流感，经过两轮传染后共有162人患了流感. 若每轮传染中平均一个人传染的人数相同.（1）试求每轮传染中平均一个人传染了几个人？（2）如果按照这样的传染速度，经过三轮

传染后共有多少个人会患流感？

分析：（1）设平均一人传染了x人，根据有一人患了流感，经过两轮传染后共有162人患了流感，列方程求解；（2）根据（1）中所求数据，进而表示出经过三轮传染后患上流感的人数.

解：（1）设平均一个人传染x人，

由题意可得2（1+x）2=162，

解得x=8，x2=-10（不合题意，舍去），

答：每轮传染中平均一个人传染8人.

（2）162×（1+8）=1458（人），

答：经过三轮后共有1458人患流感.

点评：本题属于疾病传染问题，初始值是2个人经过两轮传染后共有162人患了流感， 传染的速度是相同的，因此设出传染速度为x，即根据公式列方程求解.同理第二问还可以根据第三轮传播后的量=传播前的量×（1+传播速度）3求解.

三、销售利润问题

例3某海鲜排挡购进一批大龙虾和海胆，它们的进货单价之和是360元.大龙虾零售单价比进货单价多40元，海胆零售单价比进货单价的1.5倍少60元，按零售单价购买大龙虾2只和海胆4个，共需要1200元.（1）求大龙虾和海胆的进货单价；（2）该海鲜排挡平均每天卖出大龙虾20只和海胆12个.经调查发现，大龙虾零售单价每降低1元，平均每天就可多售出大龙虾2只，海鲜排挡决定把大

龙虾的零售单价下降a（a>0）元，海胆的零售单价和销量都不变，在不考虑其他因素的条件下，当a为多少时，海鲜排挡每天销售大龙虾和海胆获取的总利润为1490元？

分析：（1）设大龙虾进货单价为x元，海胆的进货单价为y元，由它们的进货单价之和是360元和按零售单价购买大龙虾2只和海胆4个，共需要1200元，列出方程组，即可求解；（2）由海鲜排档每天销售大龙虾和海胆获取的总利润为1490元，列出方程可求解.

解：（1）设大龙虾进货单价为x元，海胆的进货单价为y元，由题意列出方程组：

答：大龙虾进货单价为200元，海胆的进货单价为160元.

（2）由题意列出方程：（20+2a）（40-a）+12×（1.5×160-60-160）=1490，

整理得a2-30a+225=0，

解得a=15.

故当a=15时，海鲜排档每天销售大龙虾和海胆获取的总利润为1490元.

点评：本题的第一问和第二问分别考查的是二元一次方程和一元二次方程的应用. 注意关键词“多、少、降低、下降”才能正确列出代数式，进而根据关系式列方程求解.

总之，列一元二次方程解实际应用问题需要先把实际问题转化为数学问题，然后用含未知数的代数式表示未知量与已知量.在这个过程中要特别注意关键词语，如“多、少、快、慢、和、差、倍、分、超过、剩余、增加、减少”等，接着根据一些常用公式或特殊的等量关系，如传播问题、销售利润问题、增长率问题中的等量关系建立方程模型，最后解方程，并根据实际意义检验解的合理性.