如何借助二次函数的图象解答与抛物线有关的不等式关系问题

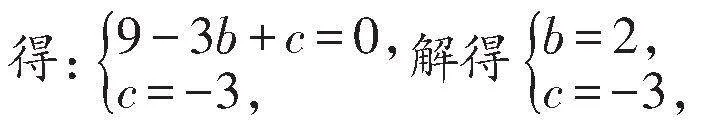
以二次函数为载体的综合性问题是中考的必考问题，一般具有考查内容广、综合性强、难度大的特点.它主要考查同学们对二次函数概念的理解、对解二次方程方法的运用以及对二次函数图象和性质的理解.本文选取了二次函数综合题中一类与抛物线有关的不等式关系问题，探讨了比较两个二次函数值的大小，以及由不等关系求自变量的取值范围这两类问题的解答方法.

那么如何借助二次函数的图象解答与抛物线有关的不等式关系问题呢？下面一起来探讨.

一、比较二次函数值的大小

例1已知抛物线y=ax2-2x+1（a≠0）的对称轴为直线x=1.

（1）求a的值；

（2）由（1）可知，抛物线的解析式为：y=x2-2x+1=（x-1）2，

因为a=1>0，所以抛物线的开口向上，

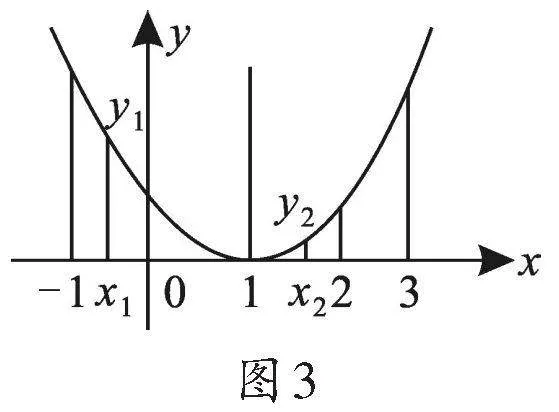
则当x>1时，y随x的增大而增大；当x<1时，y随x的增大而减小，如图3所示.

因为-1<x1<0，1<x2<2，

所以1<1-x1<2，0<x2-1<1，

结合函数图象可知，x1距离对称轴较远，所以对应的函数值y1较大，

所以y1>y2.

评注：先将抛物线的解析式配凑为顶点式：y=（x-1）2，据此即可确定抛物线的开口方向、对称轴、图象;再根据x1、x2的范围确定点M、N的位置；最后比较出x1、x2与对称轴之间的距离即可解题.

二、由不等关系求自变量的取值范围

由不等关系求自变量的取值范围，往往需先从不等关系入手，将其化简为一元二次不等式，且使其右边为0，即形如ax2+bx+c>0或ax2+bx+c<0的不等式;然后画出二次函数y=ax2+bx+c的图象，通过研究二次函数图象中点的位置及其关系，来找到满足题意的x的值，从而确定自变量的取值范围.

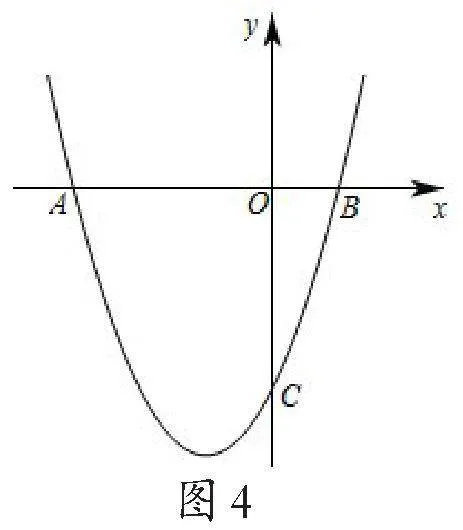
例2如图4，抛物线y=x2+bx+c与x轴

交于A（-3，0）、B两点，与y轴交于点C（0，-3）.

（1）求抛物线的解析式;

（2）结合图形，求y>0时自变量x的取值范围．

解：（1）将点A（-3，0），C（0，-3）代入抛物线y=x2+bx+c，

则抛物线的解析式为：y=x2+2x-3.

（2）令y=0，可得x2+2x-3=0，

解得x1=-3，x2=1，则B（1，0），

因为A（-3，0），B（1，0），且抛物线的开口向上，

所以当y>0时自变量x的取值范围为x<-3或x>1.

评注：令y=0，通过解一元二次方程x2+2x-3=0求得点B的坐标.而由二次函数的图象可知，要使y>0，需使抛物线上的点都在x轴的上方，即A点左侧的部分以及B点右侧的部分.

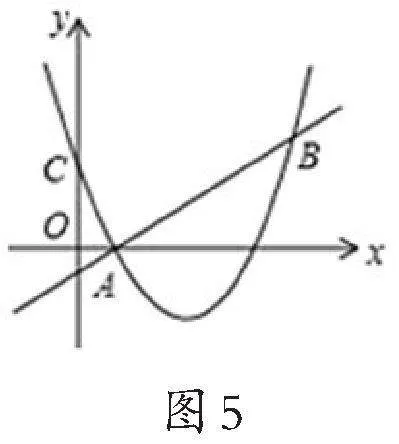
例3如图5，二次函数y=x2-4x+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b与二次函数的图象交于点A（1，0）及点B.则满足

kx+b≥x2-4x+m的x的取值范围是（ ）．

A.x≤1或x≥4

B.1≤x≤4

C.x≤1或x≥5

D.1≤x≤5

解：由y=x2-4x+m可知抛物线的对称轴为直线x=2，

∵点B和点C关于直线x=2对称，且C的横坐标为0，

∴点B的横坐标为4，

∵点A的横坐标为1，

由图可知，当1≤x≤4时，直线AB始终在抛物线的上方，此时kx+b≥x2-4x+m，故选B项.

评注：借助图形，将不等式问题转化成两个函数的不等关系问题，即可根据二次函数图象的对称性以及两个函数图象之间的关系，求出满足条件的x的取值范围.

总之，解答与抛物线有关的不等式关系问题，要熟练掌握二次函数的图象及其性质特点，借助图象来研究、分析问题，同时还要灵活运用数形结合思想、方程思想，将抛物线与二次函数的解析式、图象，二次不等式、二次方程关联起来，寻找解题的思路.