基于TLS引入局部密度因子的落叶松削度方程构建

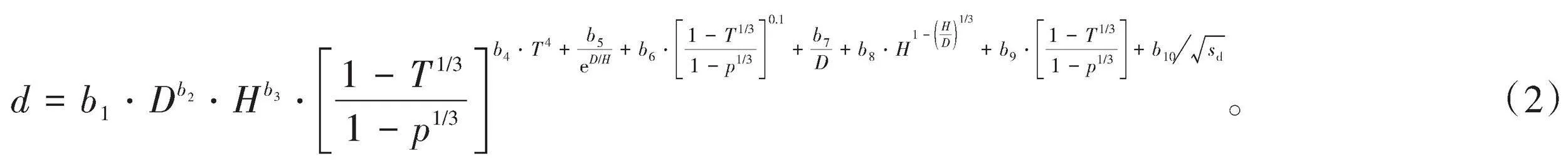
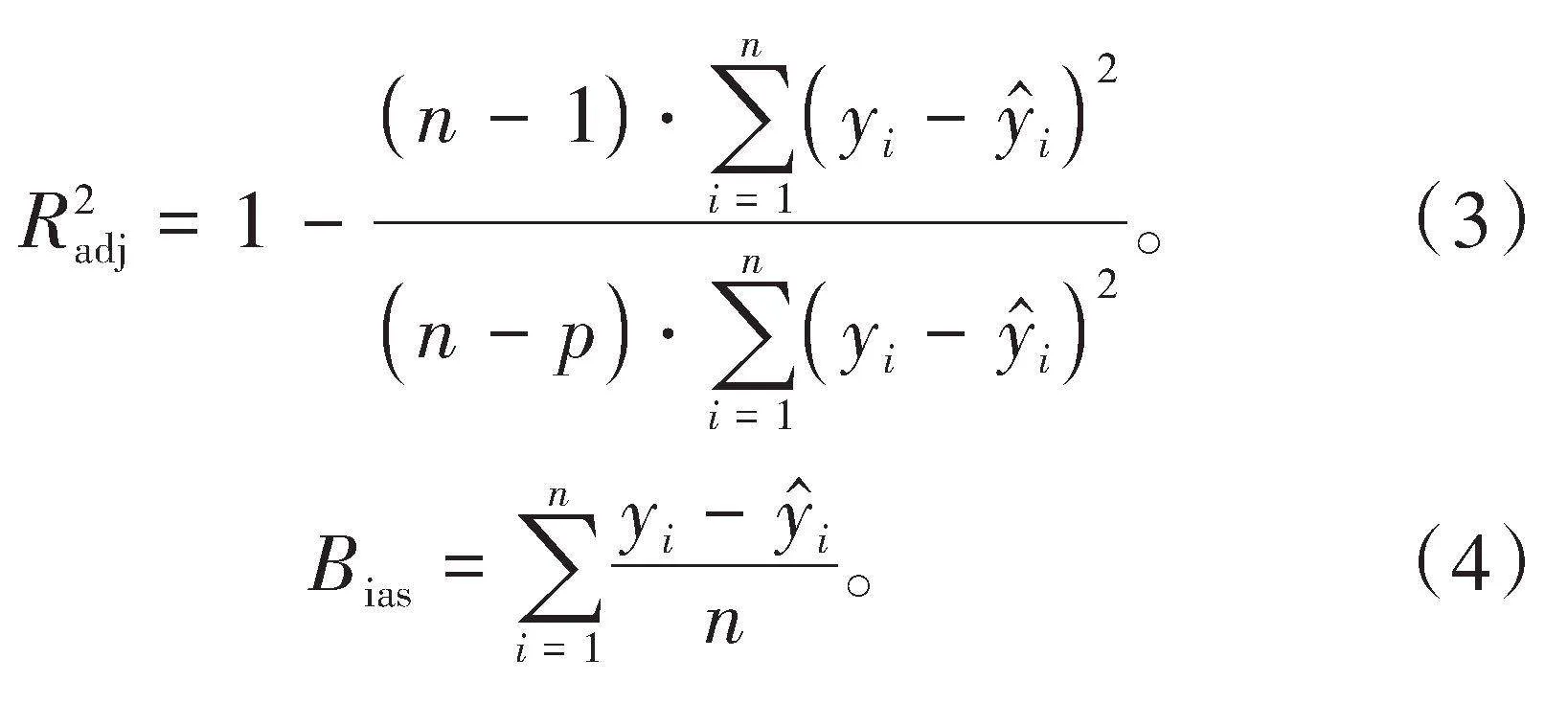
摘 要：将局部密度因子引入削度方程，通过地基激光雷达对黑龙江省佳木斯市桦南县孟家岗林场5块落叶松人工林进行扫描，采集的点云数据用于提取落叶松树高、胸径以及不同相对高度处直径，基于Kozak可变指数削度方程构建引入局部密度因子的削度方程，削度方程拟合结果为调整决定系数=0.935，均方根差RMSE=0.735 6，平均偏差Bias=0.869 3。研究表明，引入局部密度因子的削度方程具有良好的拟合精度；对比传统Kozak削度方程和引入全局密度因子的削度方程，引入局部密度因子的削度方程拟合效果更好；落叶松的削度方程其局部密度因子的计算范围与树高和胸径呈正相关。试验结果可以为孟家岗林场科学合理的造材提供理论依据，初步揭示了局部密度因子对于落叶松树干干形的影响。

关键词：落叶松人工林； 地基激光雷达； 削度方程； 局部密度因子； 邻域

中图分类号：S757.9 文献标识码：A DOI：10.7525/j.issn.1006-8023.2024.05.001

Construction of Taper Equation for Larix olgensis Using Local Density Factor Based on TLS

Abstract： By introducing the local density factor into the taper equation， five Larix olgensis plantations in Mengjiagang Forest Farm， Jiamusi City， Heilongjiang Province， were scanned by TLS. The tree height， diameter at breast height and diameter at different relative heights of Larix olgensis were extracted from the collected point cloud data. Based on Kozak variable exponential taper equation， a taper equation with local density factor was constructed， and the fitting result was =0.935， RMSE=0.735 6， Bias=0.869 3. The research showed that： the taper equation model with local density factor had good fitting accuracy， Compared with the traditional Kozak taper equation model and the taper equation model with global density factor， the taper equation model with local density factor had better fitting effect. The calculation range of the local density factor of the Larix olgensis taper equation was positively correlated with tree height and diameter at breast height. The experimental results can provide a theoretical basis for scientific and reasonable timber production in Mengjiagang Forest Farm， and preliminarily reveal the influence of local density factor on the trunk shape of Larix olgensis.

Keywords： Larix olgensis plantation； TLS； taper equation； local density factor； neighborhood

0 引言

树干削度方程是林学领域中的重要工具，常用于描述树干直径与树高之间的关系，是森林资源管理和经营决策中重要的数学模型，多用于满足对森林生态系统的深入研究以及对木材生产和可持续管理的需求。根据树干削度方程的发展历程，其模型可以归为3类，即简单削度方程、分段削度方程和可变参数削度方程，其中，可变指数削度方程能够实现更好的拟合效果，已在诸多学者的研究中得到证明［1-6］。可变指数削度方程［1-4］主要是在构建连续函数的基础上，通过调整独立变量的指数参数，实现对树干形状的准确估计，具有良好的拟合能力，因而具有更广泛的应用前景。Kozak［7］建立了一个预估树干材积的可变指数削度方程，不仅结构简单且拟合精度高，被广泛地应用到不同地区以及不同树种的削度方程拟合工作中去，为众多研究提供了重要的参考价值。

树干的削度不仅与不同的树种有关，其还受到不同树龄、地域和林分密度等重要林分经营因子的影响，并且树木的冠幅以及枝下高等树干特征也会导致树干削度的变化，因此在构建树干削度方程中考虑以上因素具有重要性和必要性。有学者研究证明，林分密度对树干削度产生的影响更为显著［4，8-9］，因此在削度方程构建过程中引入林分密度变量能够提高对树干削度的拟合精度，同时也对于树干干形形成受林分密度的影响与作用进行了解释与说明。比如在基于可变指数削度方程的黑云杉（Picea mariana）树干干形拟合工作中，在模型构建中引入了密度变量，从而实现了更高精度的拟合效果，并且进一步揭示了林分密度与树干干形削度的关系［4，10］。此外在构建落叶松的削度方程构建工作中，有学者利用分段削度方程，并在构建过程中引入冠长率和密度因子2个变量［11］，其试验结果证明了冠长率和密度因子的引入对落叶松削度方程的构建工作带来了有效的提升，实现了更高精度的预测［12］。然而在现有引入密度因子的削度方程构建工作中，通常只考虑了全局密度因子，即对于样地中的单株树木都采用整块样地的密度，未考虑样地局部密度的差异性。

地基三维激光扫描技术（Terrestrial Laser Scanning，TLS）是一种全新三维技术［13］，具有精度高、采集速度快且机动性强等优势，在林业生产调查等各个领域被广泛应用。激光雷达是遥感领域的一项前沿新技术，其通过高频发射激光束并接收目标反射回波，从而快速获取林木的三维信息，具体为通过扫描生成点云数据并利用点云数据提取树高、胸径（DBH）、冠幅等树木测量因子［14］，从而得到高精度的三维森林结构模型。在森林管理中，相较于传统的树木测量和野外调查方法，激光雷达技术的发展减少了大量森林资源清查的野外工作量和成本。

落叶松（Larix olgensis）目前已被选作我国东北地区的主要用材林树种并大量种植。因其木材优良、生长周期短和耐寒耐贫瘠等特性［15］，据统计，我国东北大部分林区已改造为落叶松纯林，是我国主要的速生丰产落叶松林基地。鉴此，通过地基激光雷达对孟家岗落叶松密度试验林进行扫描，将获取的点云数据提取密度、树高和胸径等参数。针对现有的削度方程未考虑密度因子或仅考虑全局密度因子的问题，本研究构建了针对落叶松的引入局部密度因子的可变指数削度方程，探究了局部密度因子对于落叶松树干干形的影响，为落叶松林高效培育提供科学定性及定量依据。

1 研究区域与数据处理

1.1 研究区域概况

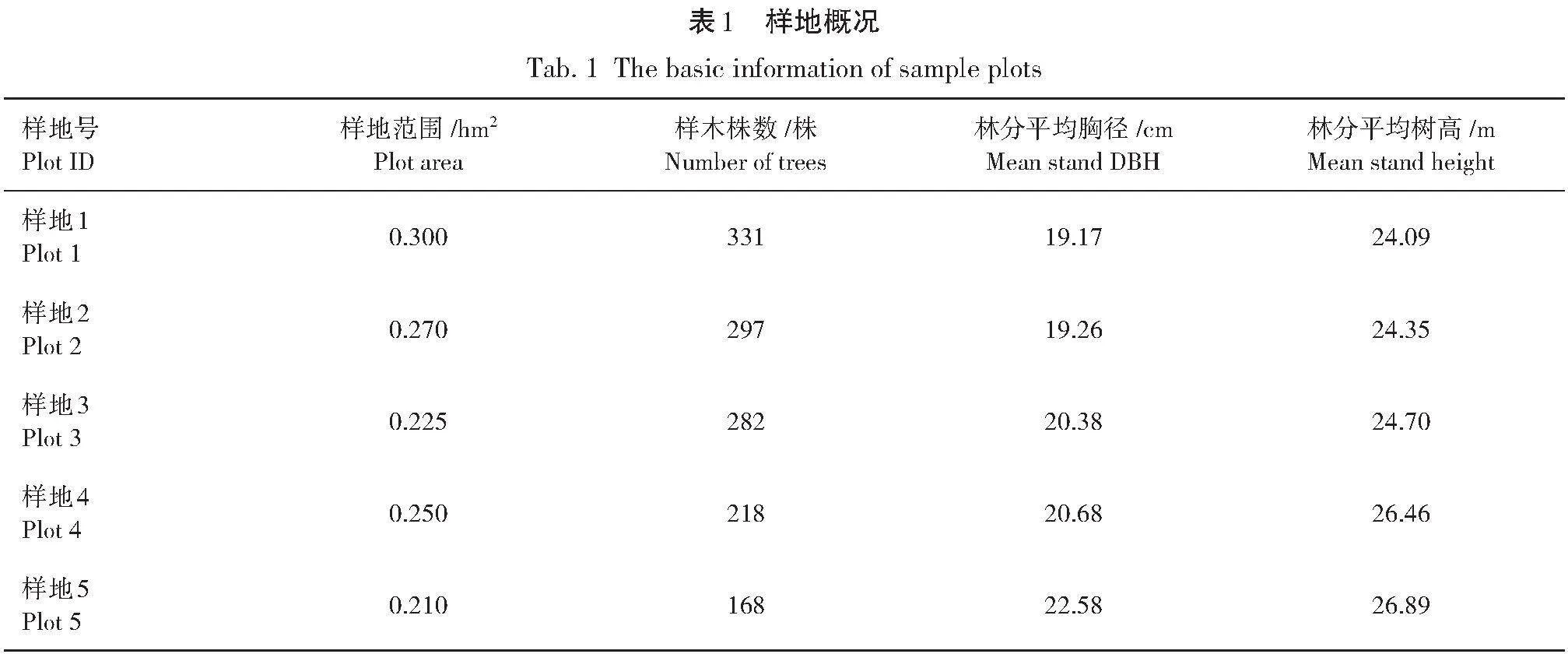
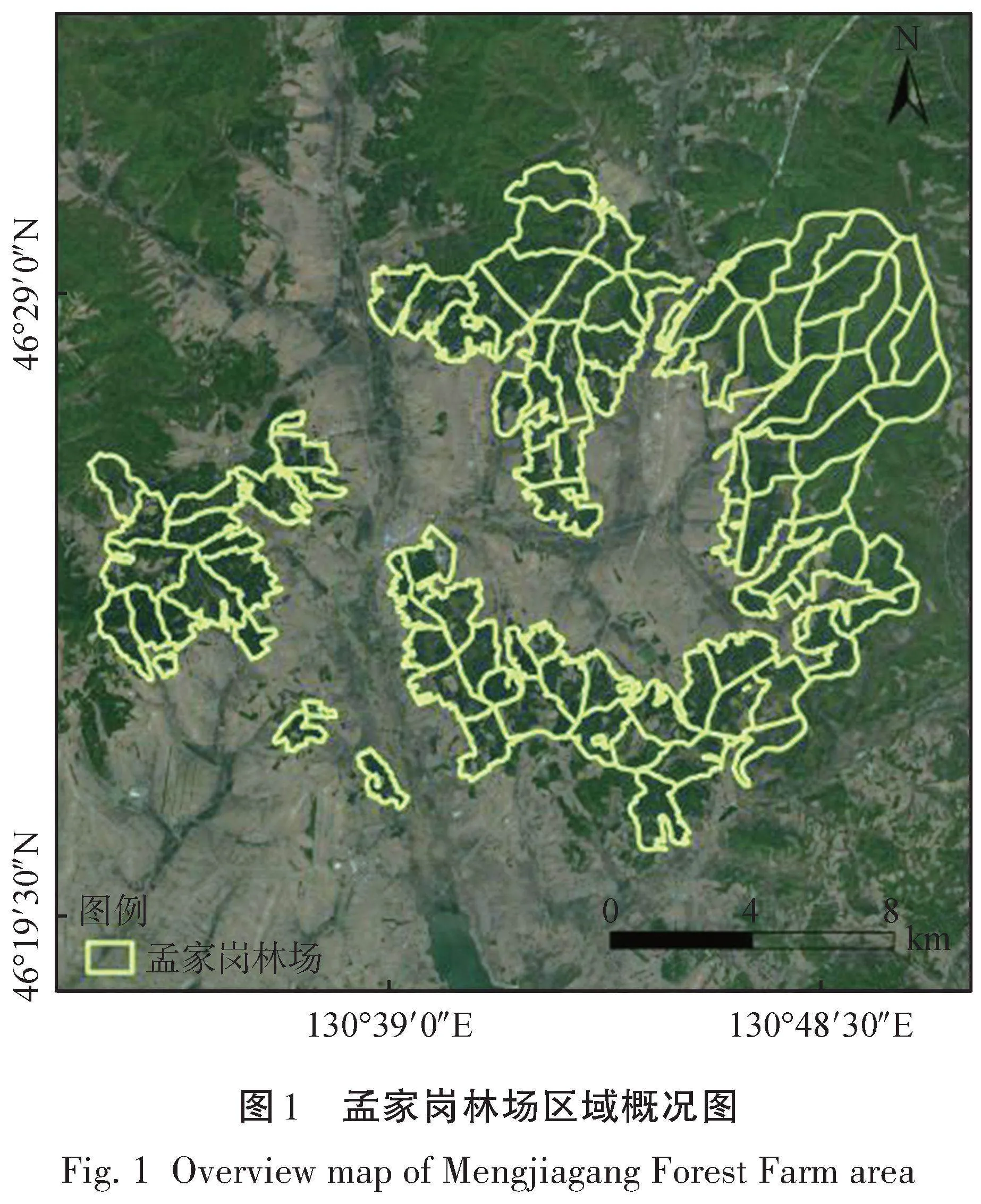
本研究选取位于黑龙江省佳木斯市孟家岗林场（130°32′～130°52′E，46°20′～46°30′N）作为试验林，区域概况如图1所示，其气候属于东亚大陆形季风气候，年平均降水量550 mm，年平均气温2.7 ℃。孟家岗林场是以针叶树为主的人工林用材基地，主要是落叶松、红松（Pinus koraiensis）、樟子松（Pinus syivestris），其中落叶松占60%。使用地基激光雷达（TLS）Riegl VZ-400i对5块密度不同的试验林进行扫描，数据概况见表1。

1.2 数据预处理

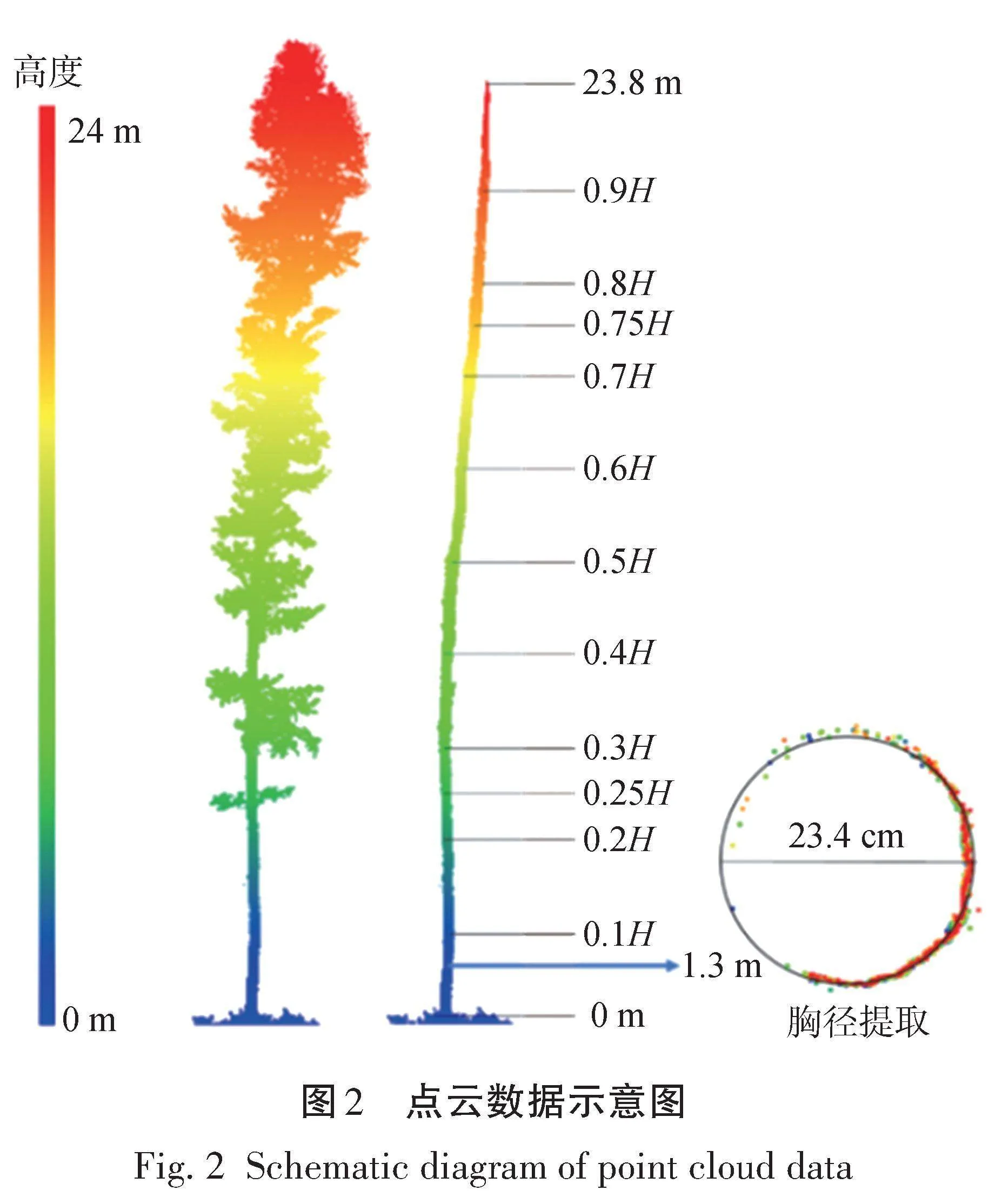
本研究采用的地基激光雷达为Riegl VZ-400i，数据采集利用多站点扫描的方式获取覆盖试验样地的多角度采集的点云数据，然后利用TLS单点点云配准算法将多站点点云数据进行点云拼接，从而获取完整的样地点云数据。然后利用LiDAR360软件（4.1版本）对样地点云数据进行预处理，主要包括点云去噪处理（剔除显著离群点噪声）、点云重采样（改善点云密度，降低数据冗余）、点云滤波（提取地面点和非地面点）、利用地面点构建数字高程模型、点云归一化（去除地形起伏影响）以及点云单木分割（提取单木点云）。基于单木点云数据，首先提取全树高H，然后利用霍夫变换［16］提取0 m、0.02H、0.04H、0.06H、0.08H、0.1H、0.2H、0.25H、0.3H、0.4H、0.5H、0.6H、0.7H、0.75H、0.8H、0.9H处直径以及1.3 m处胸径，如图2所示。

2 削度方程

2.1 基础模型

基于以往学者对东北落叶松人工林干形削度方程的研究［17-20］，选择Kozak可变指数削度方程作为基础模型，模型表达式见式（1）

式中：d为树高h处的树干直径，h为从地面算起的树干高度；D为胸径；H为全树高；T=h/H为相对树高；p=1.3/h；b1、b2、b3、b4、b5、b6、b7、b8、b9为待估计参数。

2.2 包含局部密度因子的削度方程构建

Kozak可变指数削度方程通过改变指数项参数实现对不同树高处树干直径的拟合，类似的考虑在削度方程的指数部分引入密度因子，从而表征密度因子与树干干形之间的关系与规律［4］。为了研究密度因子与树干削度之间的联系，张森森等［21］设计了

由于样地中不同区域的密度不一，本研究采用统计单株落叶松局部邻域的密度方法获得局部密度因子，相比于统计样地的全局密度，局部密度因子更符合单株树木真实环境，能够获得更精确的削度方程。同时为了研究单木受到周围环境的影响范围，统计不同半径范围内的密度作为密度因子拟合削度方程，本研究中分别统计2、3、4、5、6、7、8、9、10、11、12 m半径范围内的密度。

3 试验设置与结果分析

3.1 试验设置

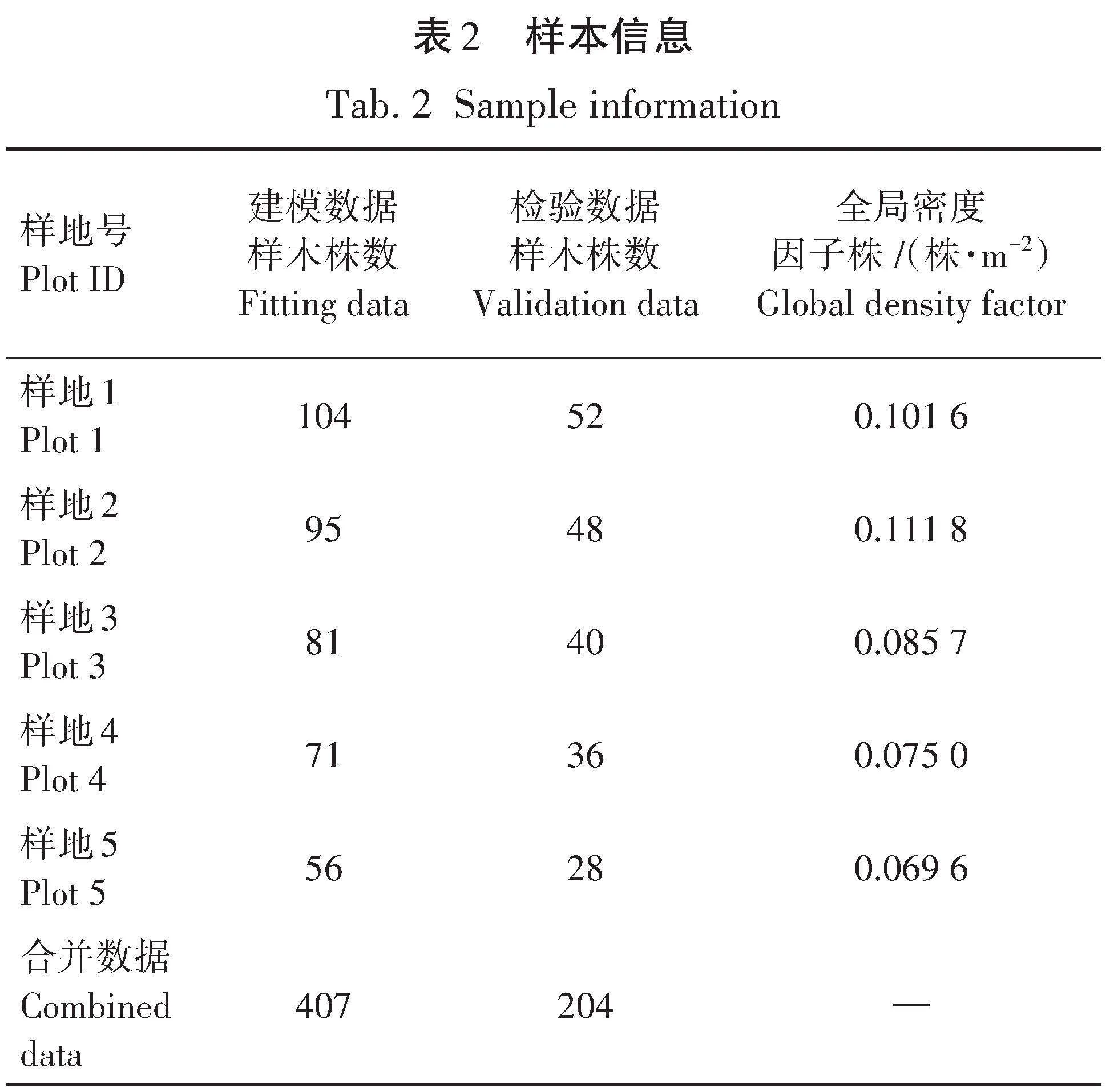
本研究中选取每块样地的中心区域（为计算局部密度因子），然后在5块样地中心区域分别随机选取2/3数据，并将不同样地选取的数据合并作为建模数据，其余1/3数据合并作为检验数据；此外对于全局密度因子的统计，将每块样地的全局密度作为对应样地中单株落叶松的密度因子，其具体信息见表2。

评价指标：采用调整决定系数（）、平均偏差（Bias，式中记为Bias）、均方根误差（RMSE，式中记为RMSE）作为评价模型的统计量指标。各统计量指标计算公式为

3.2 引入局部密度因子的削度方程拟合

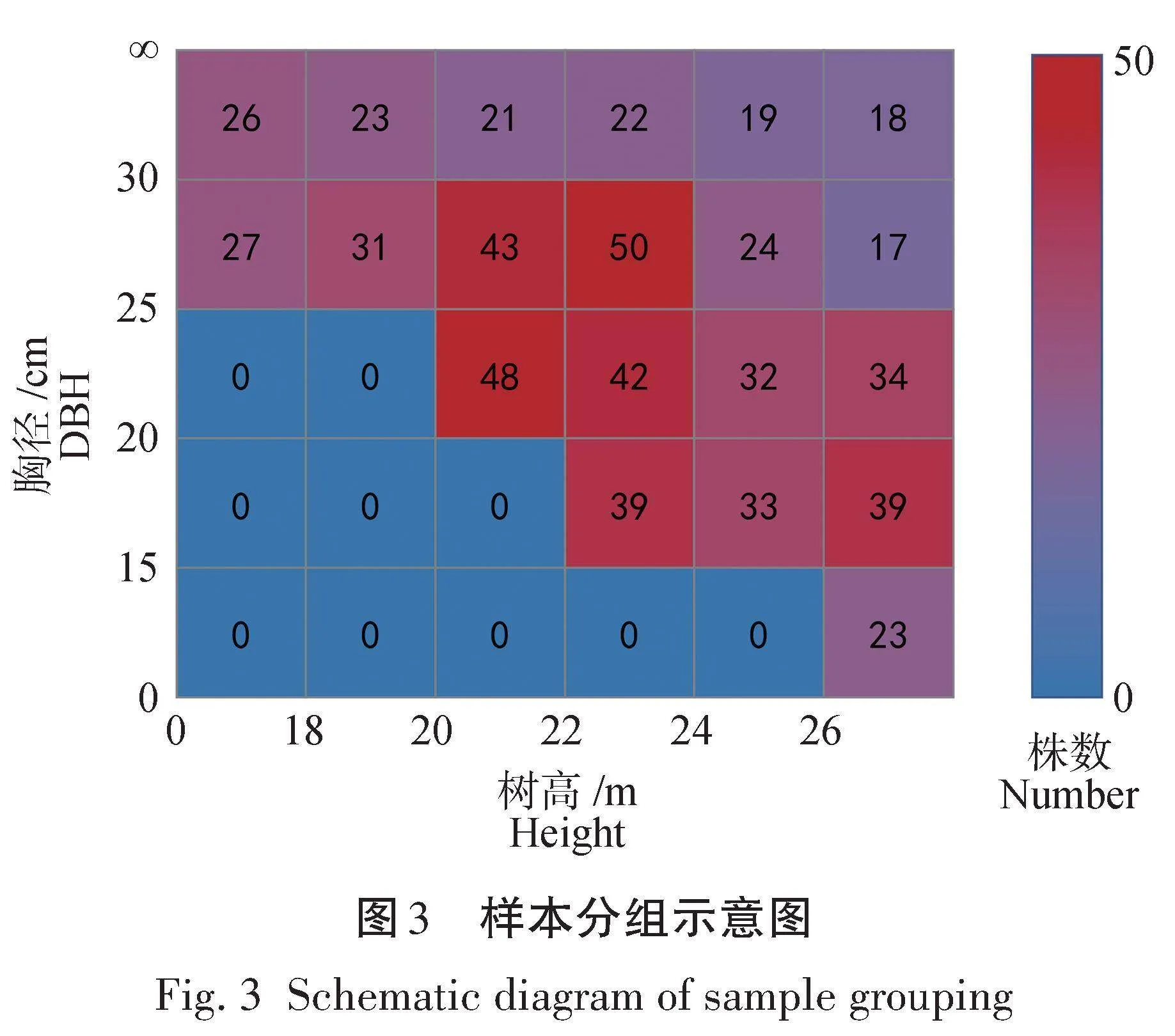
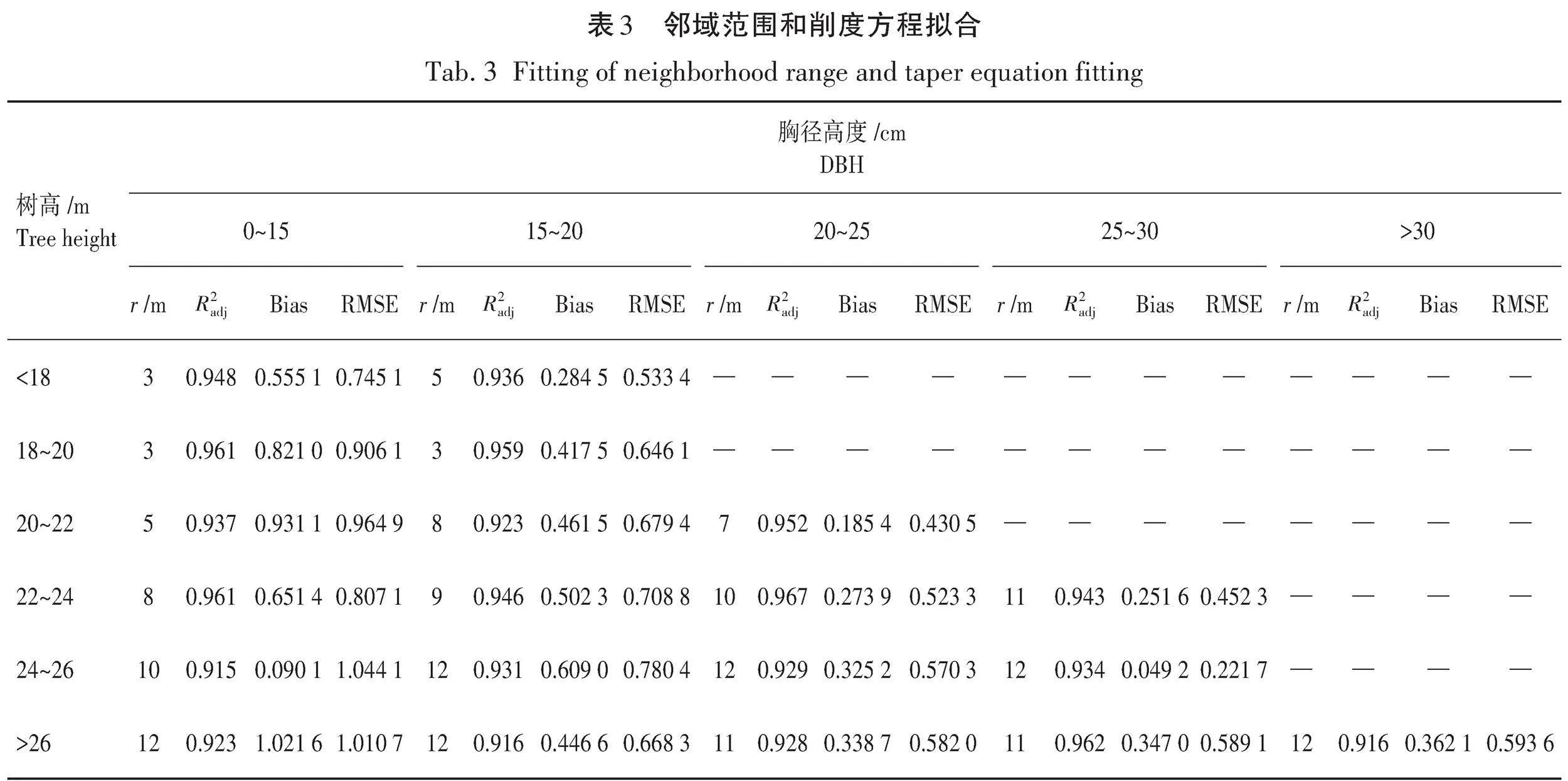
对样本数据进行了包含局部密度因子的削度方程拟合，为探究局部密度因子计算范围对于削度方程拟合精度的影响，将样本按照不同树高和胸径进行分组拟合，其分组情况如图3所示。然后根据式（2）分别计算了引入不同计算范围局部密度因子的削度方程拟合结果，表3列出了不同胸径和树高情况下最优密度因子计算范围，图4示意了最优局部密度因子计算范围分别和树高（TH）和胸径（DBH）的相关性，图5展示了按照树高分组的样本拟合残差。由分析结果可以看出，不同胸径和树高的削度方程拟合使用的最优局部密度因子范围不同，每组样本都取得了良好的拟合结果，其均大于0.9。根据看出TH（22～24 m）和DBH（20～25 cm）的样本其削度方程拟合结果最好，=0.967，RMSE=0.523 3，Bias=0.273 9。而TH（24～26 m）和DBH（0～15 cm）的样本拟合效果较差，但其仍达到了0.915，RMSE=1.044 1，Bias=1.090 1；此外TH（>26 m）和DBH（0～15 cm）的样本拟合效果也稍差，其=0.923，RMSE=1.010 7，Bias=1.021 6。这是因为对于树高越高的树，其胸径通常越大，以上2组数据其胸径较小，这可能是由于生长环境、光照及土壤等原因造成其主干生长异常，从而进一步导致了削度方程拟合效果较差。通过分析图4可以看出，最优局部密度因子（γ）计算范围与胸径和树高具有一定的相关性，总体趋势为随着树高的增高和胸径的增大，其密度因子计算范围越来越大，其中密度因子计算范围随着树高增高而增大的趋势更为明显，其相关性更强，密度因子计算范围从3 m增加到了 12 m，这说明树高越高其主干干形将被越大邻域范围内的其他树木所影响。

3.3 不同削度方程的拟合与检验

根据以上分析对检验数据进行了包含局部密度因子的削度方程拟合检验，并将其与不包含密度因子和包含全局密度因子的削度方程拟合结果进行比较，其拟合结果和检验结果见表4，其中GD-Kozak（Global Density-Kozak）表示全局密度因子，LD-Kozak（Local Density-Kozak）表示局部密度因子。由表4可以看出，原始Kozak削度方程的拟合效果最差，其模型拟合的为=0.851，RMSE=1.748 5，Bias=3.057 3，模型检验的结果为=0.823，RMSE=1.879 6，Bias=3.163 5。使用全局密度因子的Kozak削度方程的拟合效果优于原始模型，其模型拟合的为=0.884，RMSE=1.535 8，Bias=2.358 7，模型检验的结果为=0.869，RMSE=1.698 5，Bias=2.496 5。而本研究提出的在Kozak模型中引入局部密度因子的方法取得了最优的拟合结果，模型拟合的为=0.935，RMSE=0.735 6，Bias=0.869 3，模型检验的结果为=0.921，RMSE=0.763 5，Bias=0.806 1。对比试验结果表明，本研究提出的引入局部密度因子的削度方程具有更好的拟合精度，能够更精确地构建落叶松削度方程。

4 结论

本研究利用地基激光雷达对黑龙江省佳木斯市桦南县孟家岗林场的5块落叶松人工林标准样地进行扫描，采集了这些人工林的点云数据。通过提取点云数据中的落叶松相对高处直径、树高和胸径等信息，构建了一种引入局部密度因子的可变指数削度方程，并在611株样本数据上进行了试验验证。研究结果显示，这种新模型具有较高的拟合精度，为林业研究和实践提供了重要参考。

1）模型拟合效果。引入局部密度因子的可变指数削度方程在样本数据上的拟合效果显著，表现出较高精度。具体指标包括：模型拟合的R为0.935，均方根误差（RMSE）为0.735 6，偏差（Bias）为0.869 3；模型检验结果为：R=0.921，RMSE=0.763 5，Bias=0.806 1。这些指标显示了模型在处理数据时的优越性能。

2）模型对比与优势。与传统的Kozak削度方程以及引入全局密度因子的削度方程相比，本研究提出的引入局部密度因子的削度方程在拟合效果上更具优势。这说明局部密度因子在模型中起到了关键作用，显著提升了模型的拟合效果。

3）局部密度因子的相关性。研究还发现，最优局部密度因子的计算范围与树木的胸径和树高有一定的相关性。总体趋势是随着树高和胸径的增大，密度因子的计算范围也随之增大。特别是密度因子的计算范围与树高的增大趋势尤为显著，呈正相关关系。

4）激光雷达的优势与局限性。激光雷达在林业应用中展现出巨大优势，包括数据密度大、精度高、抗干扰能力强和作业效率高等，使其广泛应用于森林资源的三维动态监测中。然而，激光雷达也存在一些局限性，如难以实现全三维信息的获取，以及数据处理和提取算法尚不完善。地基获取的点云数据量大，处理过程繁琐，虽然降低了外业工作时间和成本，但内业数据处理耗时较长。因此，提高林木参数的自动化获取成为未来研究的热点之一。

5）研究意义与未来方向。削度方程能够较准确地反映树干的干形。本研究利用TLS数据构建了引入局部密度因子的削度方程，对精确估计落叶松人工林的单木蓄积及合理指导造材具有重要意义。然而，模型构建时未考虑冠长率、冠长、树冠高度和形率等因素，这些因素可能对单株立木的干形产生影响。随着后续研究的开展，期望能找到综合考虑上述影响因素的最优削度方程，以进一步提高模型的精确度和应用性。

【参 考 文 献】

［1］ KOZAK A.A variable-exponent taper equation［J］.Canadian Journal of Forest Research，1988，18（11）：1363-1368.

［2］ 邹茂胜，孙毓蔓，李丹丹，等.基于地基激光雷达数据的落叶松人工林削度方程构建［J］.中南林业科技大学学报，2022，42（8）：90-100.

ZOU M S，SUN Y M，LI D D，et al.Construction of the taper equation of Larix olgensis plantations based on Terrestrial Laser Scanning data［J］.Journal of Central South University of Forestry & Technology，2022，42（8）：90-100.

［3］ BI H.Trigonometric variable-form taper equations for Australian eucalypts［J］.Forest Science，2000，46（3）：397-409.

［4］ SHARMA M，ZHANG S Y.Variable-exponent taper equations for jack pine，black spruce，and balsam fir in eastern Canada［J］.Forest Ecology and Management，2004，198（1-3）：39-53.

［5］ KOIRALA A，MONTES C R，BULLOCK B P，et al.Developing taper equations for planted teak （Tectona grandis L.f.） trees of central lowland Nepal［J］.Trees，Forests and People，2021，5：100103.

［6］ ROJO A，PERALES X，SÁNCHEZ-RODRÍGUEZ F，et al.Stem taper functions for maritime pine （Pinus pinaster ait.） in Galicia （northwestern Spain）［J］.European Journal of Forest Research，2005，124（3）：177-186.

［7］ KOZAK A.My last words on taper equations［J］.The Forestry Chronicle，2004，80（4）：507-515.

［8］ 徐衍桓.林分密度对落叶松人工林削度方程的影响［J］.林业勘查设计，2017（2）：64-65.

XU Y H.The effect of stand density on the taper equation of larch plantation［J］.Forest Investigation Design，2017（2）：64-65.

［9］ LIANG R T，SUN Y J，ZHOU L，et al.Analysis of various crown variables on stem form for Cunninghamia lanceolata based on ANN and taper function［J］.Forest Ecology and Management，2022，507：119973.

［10］ SHARMA M，PARTON J.Modeling stand density effects on taper for jack pine and black spruce plantations using dimensional analysis［J］.Forest Science，2009，55（3）：268-282.

［11］ MAX T A，BURKHART H E.Segmented polynomial regression applied to taper equations［J］.Forest Science，1976，22（3）：283-289.

［12］ JIANG L，LIU R.Segmented taper equations with crown ratio and stand density for Dahurian Larch （Larix gmelinii） in Northeastern China［J］.Journal of Forestry Research，2011，22（3）：347-352.

［13］ BIENERT A，MASS H G，SCHELLER S.Analysis of the information content of terrestrial laserscanner point clouds for the automatic determination of forest inventory parameters［C］.Workshop on 3D Remote Sensing in Forestry，2006，14：15th，Vienna.

［14］ BROLLY G，KIRÁLY G.Algorithms for stem mapping by means of terrestrial laser scanning［J］.Acta Silvatica et Lignaria Hungarica，2009，5（1）：119- 130.

［15］ 郭瑞霞.基于多源数据的落叶松人工林识别研究［D］.西安：西安科技大学，2019.

GUO R X.Research on larch plantation recognition based on multi-source data［D］.Xi′an：Xi′an University of Science and Technology，2019.

［16］ 李丹.基于地基扫描与机载成像激光雷达的森林参数反演研究［D］.昆明：西南林业大学，2012.

LI D.Forest parameters estimation using TLS and Airborne Image Lidar［D］.Kunming： Southwest Forestry University，2012.

［17］ 韩飞.落叶松人工林削度方程的研究［D］.哈尔滨：东北林业大学，2010.

HAN F.The study of taper equation for Larix olgensis plantation［D］.Harbin： Northeast Forestry University，2010.

［18］ 许延丽.兴安落叶松树干削度和树皮厚度及材积的相容可加性研究［D］.哈尔滨：东北林业大学，2019.

XU Y L.Study on additive equation of stem taper and bark thickness and compatible volume equations for Dahurian Larch［D］.Harbin： Northeast Forestry University，2019.

［19］ 刘瑞龙.兴安落叶松人工林树干削度和材积模型的研究［D］.哈尔滨：东北林业大学，2011.

LIU R L.Taper and volume models for Dahurian Larch plantations［D］.Harbin： Northeast Forestry University，2011.

［20］ 姜立春，刘瑞龙.基于非线性混合模型的落叶松树干削度模型［J］.林业科学，2011，47（4）：101-106.

JIANG L C，LIU R L.A stem taper model with nonlinear mixed effects for Dahurian Larch［J］.Scientia Silvae Sinicae，2011，47（4）：101-106.

［21］ 张森森.基于混合效应模型的可变密度可变指数削度方程构建研究［D］.北京：中国林业科学研究院，2017.

ZHANG S S.Nonlinear mixed-effects modeling of variable exponent taper equations with density for Chinese fir［D］.Beijing： Chinese Academy of Forestry，2017.