基于震源机制解的新疆地区地震烈度衰减关系研究

摘要：收集1716—2022年130次有烈度数据的破坏性地震事件，补充近期新疆区域破坏性地震烈度数据，对124幅地震烈度图，281对烈度圈长、短轴数据进行分类整理。采用数学方法拟合了新疆地区不同时间节点、不同震源机制解地震烈度衰减模型。研究发现，在烈度衰减过程中，走滑型和逆断型地震略有不同，不同的地震震源破裂性质会影响烈度衰减关系的长短轴，因此，我们可以将其作为修正因子，用于快速评估地震灾害的烈度影响场，在地震发生后，修改和完善烈度圈的长短轴数据，以便更准确地进行评估。

关键词： 烈度； 地震烈度衰减关系； 震源机制解； 地震灾害

doi：10.16256/j.issn.1001-8956.2024.03.005

在快速评估地震烈度的工作中，经常运用烈度衰减关系去判断烈度区的面积大小以及影响范围，在应急数据库的支持下，开展更有效的抢险救灾工作。针对地震烈度衰减关系的研究，国内学者通过不同的方法和手段得出不同的地震烈度衰减关系模型［1-2］。张齐等采用应用随机效应回归方法确定地震烈度衰减关系模型系数［3］。肖亮等补充了1991年之后地震资料，分长、短轴拟合了西部区域的烈度衰减关系［4］。谭明等通过对不同时段和不同区域的震例研究，计算得出了地震动的衰减关系［4］。新疆地震灾害评估一般用中国西部衰减关系计算烈度，由于新疆地域广阔，地质构造复杂多变，导致地震震源破裂形式多样［5-12］，为提高地震灾害评估模型的可靠性，选出更适合本构造区域的地震烈度衰减关系，是新疆地区地震快速评估的一项必要工作［13］。本文中补充了近期新疆区域破坏性地震烈度数据，并根据地震震源破裂性质的不同分区，结合新疆历史震例，利用强震台网记录数据回归拟合不同震源破裂性质的地震烈度衰减关系，为抗震设防和震后烈度快速评估提供有效的参考依据。

1 地震资料选取

新疆区域内地震带主要分布有北、中、南天山地震带、阿尔泰地震带和塔里木—阿拉善地震带，是中国主要的内陆地震活动地区，地震活动强烈，破坏性地震频繁发生。

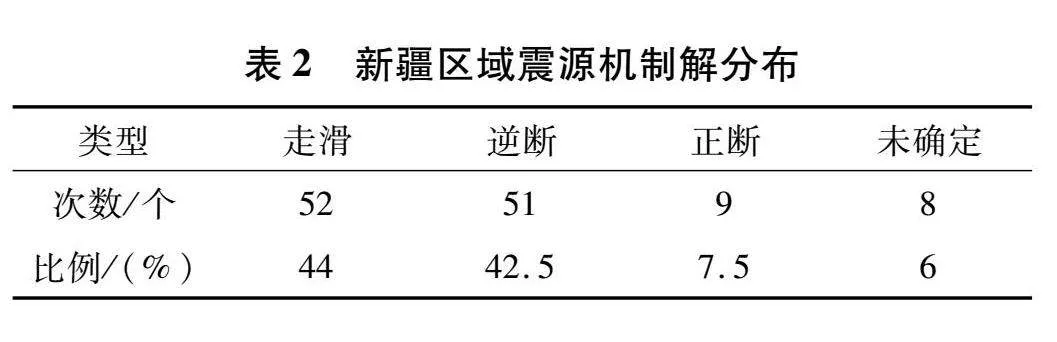
收集新疆地区1716—2022年130次有烈度数据的破坏性地震事件（个别地震在较短时间内连续发生，作为1次地震事件），130次地震事件中收集到的地震烈度图为124幅。将124幅烈度图进行数字化后，采用长轴转向的方法测量烈度圈长短轴，共计281对长、短数据，由表1可看出，数据优势范围是Ⅴ～Ⅷ度，在这个烈度区间内的数据较多。利用Cap方法反演震源机制解，通过分割波形记录为Pnl（地震P波）和Snl部分，分别赋予不同的权重，利用格点搜索的方法进行地震震源机制反演。其中有震源机制解的地震为120次，按照走滑型、逆断型、正断型和未确定型4种类型进行地震烈度衰减关系分类统计（表2），统计显示，新疆区域破坏性地震的震源破裂方式主要以逆断和走滑为主。

本文中所选地震烈度数据主要来自《新疆通志·地震志》《中国震例》《中国地震台网观测报告》和中国地震局有关资料汇编［14］，其中现有的等震线资料均来自于对相关大地震的实地考察［15］。地震震源机制解部分结果来源于高国英等对新疆中强地震震源机制解的分析［16］。

2 地震烈度衰减关系

受发生地震的地质构造和地貌环境影响，地震烈度的衰减近似为椭圆分布。根据新疆地区地震烈度数据，使用椭圆模型进行烈度衰减关系拟合，其烈度衰减模型的通用表达形式为

I=A+BM+Clg（R+R0） ·（1）

Ia=Aa+BaM+Calg（Ra+R0a） ·（2）

Ib=Ab+BbM+Cblg（Rb+R0b） ·（3）

式中：I表示烈度；M为震级；R为震中距；R0为预设常数；A、B和C为回归系数；a和b分别为长轴和短轴方向。使用不同方法所得到的地震烈度衰减关系不同，其预设常数也不同，谭明等所选取的预设常数R0a=25，R0b=15；俞言祥等［17］建立的新一代地震区划图地震烈度衰减关系中的预设常数R0a=25，R0b=13。

2.1 不同时间节点烈度衰减关系

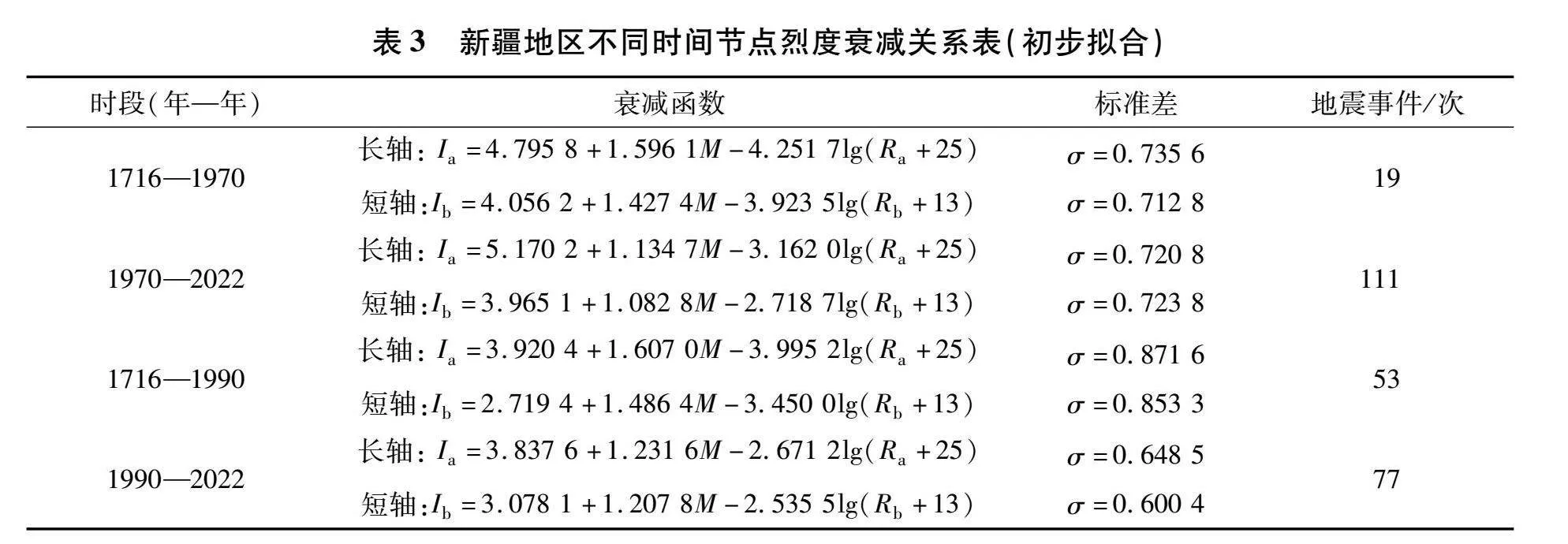
本文中根据不同的时间节点对新疆区域1716—2022年的破坏性地震分别进行烈度衰减关系拟合，得出不同的参数（表3）。由于新疆地处西北边陲，其台网的使用始于20世纪70年代，在这之前的破坏性地震灾害信息主要来源于历史记载和后期的科学考察，地震烈度分布图也是基于此绘制而成。全国数字地震台网建立之后，强震记录数据逐渐丰富，大大提高了绘制地震烈度图的精度。故本文中将1970年作为一个时间节点，分别对其前后两个时段的地震烈度数据拟合烈度衰减关系曲线（图1 a、b）。如图所示，两个时间段衰减趋势基本一致，都表现出了近、远场饱和趋势，只是1716—1970年的衰减关系曲线近场烈度过大，比1970—2022年的衰减关系曲线近场烈度高，可能与1970年前高震级烈度数据较多，低震级烈度数据有遗漏有关，但这两个烈度衰减关系曲线基本都符合实际烈度衰减规律。

此外，1990年之后，新疆区域破坏性地震频发，且记录的地震数量与之前的大致相当，将1990年作为另一个时间节点，分别对其前后两个时段的地震烈度数据拟合烈度衰减关系曲线（图1 c、d）。两个时间段近场震级饱和趋势有明显不同，主要因为新疆区域大地震主要集中在1990年之前，而1990年之后破坏性地震高震级较少，低震级低烈度数据丰富，近场烈度长短轴影响距离具有较好的一致性。从远场看来，两个衰减曲线与整体衰减有较好的一致性。

2.2 不同震源机制解的地震烈度衰减关系

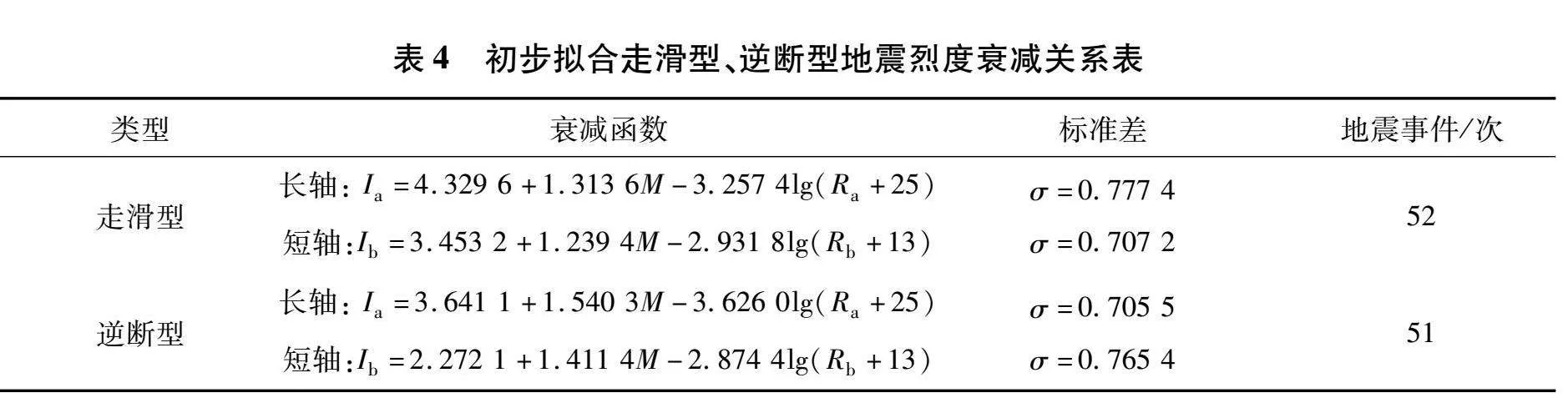
根据不同震源机制解类型数量分布（表2），新疆地区较容易形成走滑型、逆断型的地震震源破裂方式，选择走滑型、逆断型的地震烈度数据，利用最小二乘法进行地震烈度衰减关系初步拟合（表4）。如图2所示，走滑型和逆断型地震烈度衰减关系，震级饱和趋势具有明显差异，走滑型烈度衰减关系曲线近场影响表现出接近于圆的趋势；逆断型烈度衰减关系曲线在地震烈度远场影响接近于圆。

2.3 烈度衰减曲线头尾限定计算

2.3.1 头尾限定方法

通过头尾限定方法对衰减曲线进行头尾限定，能够更加贴近实际工程需求，从而提高衰减曲线的精准度，是进行烈度衰减关系研究至关重要的一步。常用的衰减曲线头尾限定方法一种是在曲线的头尾处增加样本点，另一种是使用两部拟合法来进行限定。本文中采用的烈度衰减数据大部分分布在Ⅴ～Ⅷ度内，优势明显，在曲线头尾增补样本点会影响烈度数据的整体优势，样本点的多少也不好控制，因此，本研究采用数学方法对烈度衰减曲线进行头尾限定处理。限头：当短轴方向无限接近零时，长轴方向与短轴方向无限接近但不等于零，这时椭圆形状变为一条所有烈度值都相等的线段。在计算时，通常将最小的短轴值设为1；限尾：当短轴和长轴无限增长时，形状从椭圆变成圆，烈度值都会相互对等，在计算中，可以选取合适的数值作为R，M为地震震级，计算公式［18］为

R=10（0.22M+1.11） ·（4）

2.3.2 烈度衰减曲线头尾限定计算

对走滑型、逆断型地震烈度衰减关系结果进行头尾限定修正，以走滑型衰减关系公式（5）、（6）为例。

长轴： Ia=4.329 6+1.313 6M-3.257 4lg（Ra+25） · （5）

短轴：Ib=3.453 2+1.239 4M-2.931 8lg（Rb+13） · （6）

从表1可知，由于地震烈度数据的优势范围为Ⅴ～Ⅷ度，而高烈度和低烈度的数据又比较稀少，所以在近场区域内的高烈度曲线头部虽然呈明显饱和态势，却又没有相交，这不符合震中烈度双高饱和规律。在远场尾部的衰减关系曲线，随着震中距的增大，长短轴并没有显示出无限接近的态势且在较低烈度也没有交叉现象，这与实际结果并不一致（图2）。利用头尾限定方法对公式（5）、（6）进行修正。具体方法如下：

（1） 本次数据采集到的历史破坏性地震最高震级为8.2级，最低为4.6级，故有式（6）中令M=M1=8.2，R=Rb0＝1，得I1＝10.25，将Ia＝l1＝10.25，M=8.2数值代入到公式（5）中，计算出Ra0＝5.85，这就代表最里面的烈度曲线为椭圆的短半轴b=1时，长半轴a=5.85；

（2） 令M=M1=8.2，利用公式（4）计算出R1＝820.35，分别将数值代入到公式（5）、（6）中，计算出Ia=5.56，Ib=5.05，在R1处将I2＝（Ia+Ib）/2=5.3为曲线尾部；

（3） 令M=M2=4.6， 利用公式（4）计算出R2＝132.43， 将数值代入到公式（5）、（6）中，计算出Ia=2.84，Ib=2.81，在 R2处将I2＝（Ia+Ib）/2=2.82为曲线尾部；

（4） 把上述计算所得数据代入到椭圆长轴的衰减公式（7）：

I1=A1+A2M1-A3lg（Ra0+25）

I2=A1+A2M2-A3lg（R1+25）

I3=A1+A2M3-A3lg（R2+25） ·（7）

求得A1＝4.433 8，A2＝1.334 4，A3＝3.439 6。

接着把上述计算所得数据代入到椭圆短轴的衰减公式（8）：

I1=B1+B2M1-B3lg（Rb0+13）

I2=B1+B2M2-B3lg（R1+13）

I3=B1+B2M3-B3lg（R2+13） ·（8）

求得B1＝3.403 6，B2＝1.224 5，B3＝2.784 3。

（5） 把上述求得系数代入衰减公式，得到头尾限定修正后的走滑型衰减关系。用同样方法得到逆断型修正后的衰减关系（表5）。

3 对比分析

3.1 与前人结果的对比

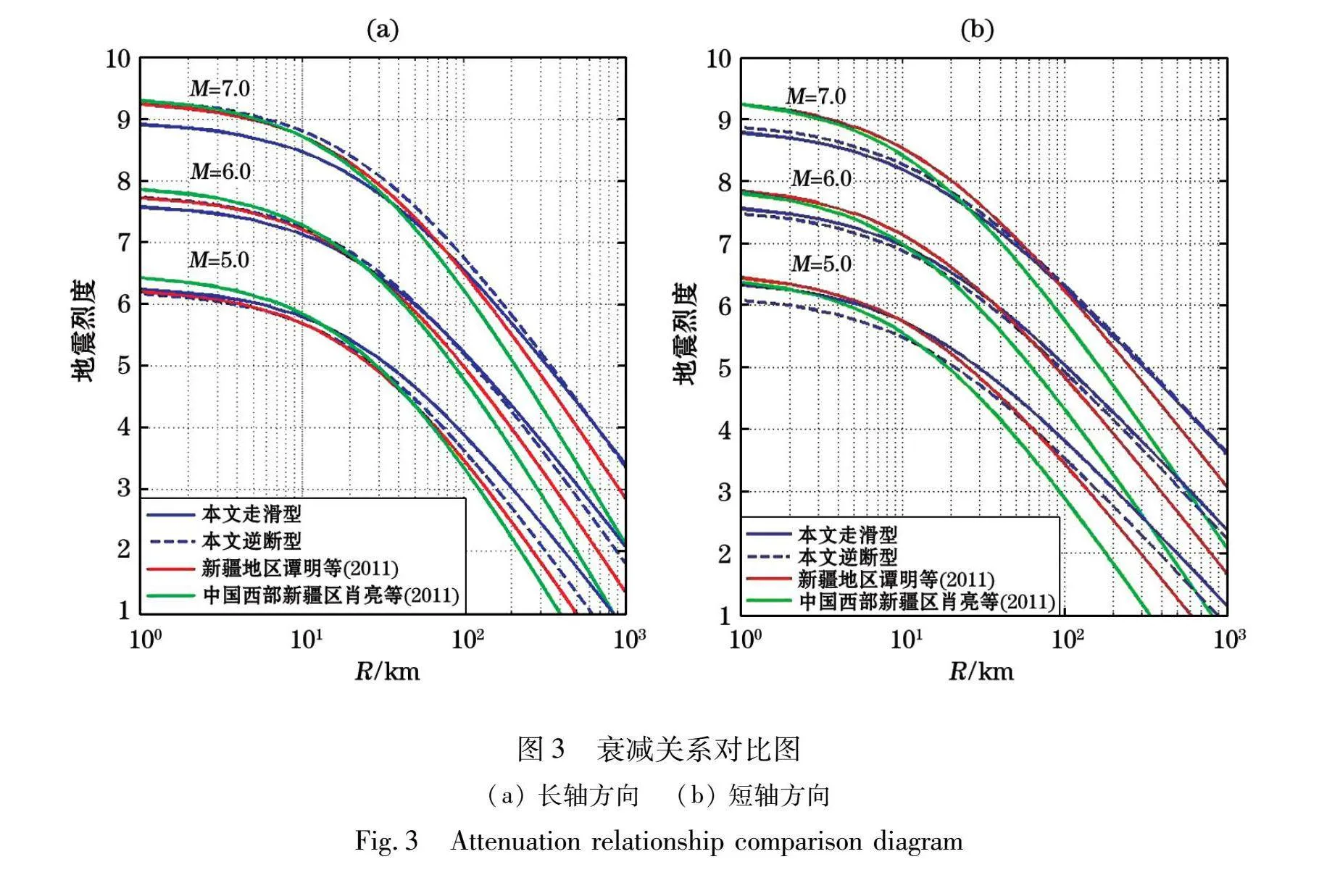
目前，在新疆快速评估地震烈度的工作中，一般用谭明的烈度衰减模型（式9、10）。此外，肖亮等补充了1991年之后地震资料，分长、短轴拟合了西部区域的烈度衰减关系（式11、12），故本文中将所得到的走滑型、逆断型地震烈度衰减关系统一与谭明的新疆地区烈度衰减关系以及肖亮的西部地区新疆地区衰减关系进行对比分析（图3）。

Ia=4.269 7+1.515 7M-3.990 2ln（Ra+25）·（9）

Ib=3.243 8+1.399 6M-3.314 2ln（Rb+13）·（10）

Ia=5.601 8+1.434 7M-4.489 9ln（Ra+25）·（11）

Ib=3.611 3+1.434 7M-3.847 7ln（Rb+13）·（12）

图3给出了谭明、肖亮的地震烈度衰减关系与本文中衰减关系的对比结果。对比发现，本文中逆断型模型与谭明的新疆地区衰减模型基本一致。在震中附近，本文中两种模型的烈度值明显低于肖亮衰减模型。当R>50 km 时，肖亮烈度衰减曲线逐渐低于本文中两种模型衰减曲线和谭明烈度衰减曲线。随着震中距的增加，肖亮烈度衰减速度明显快于本文中两种模型和谭明模型。

3.2 实际地震检验对比

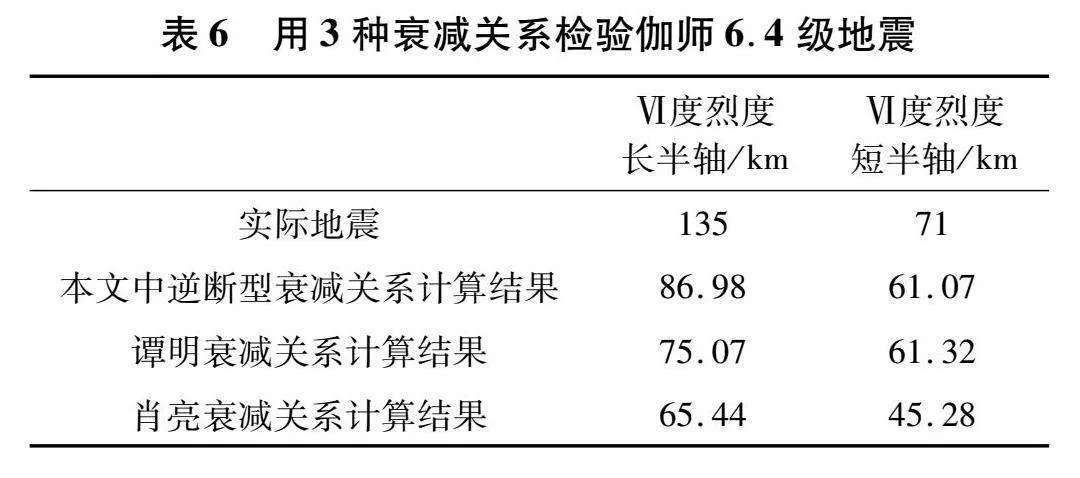
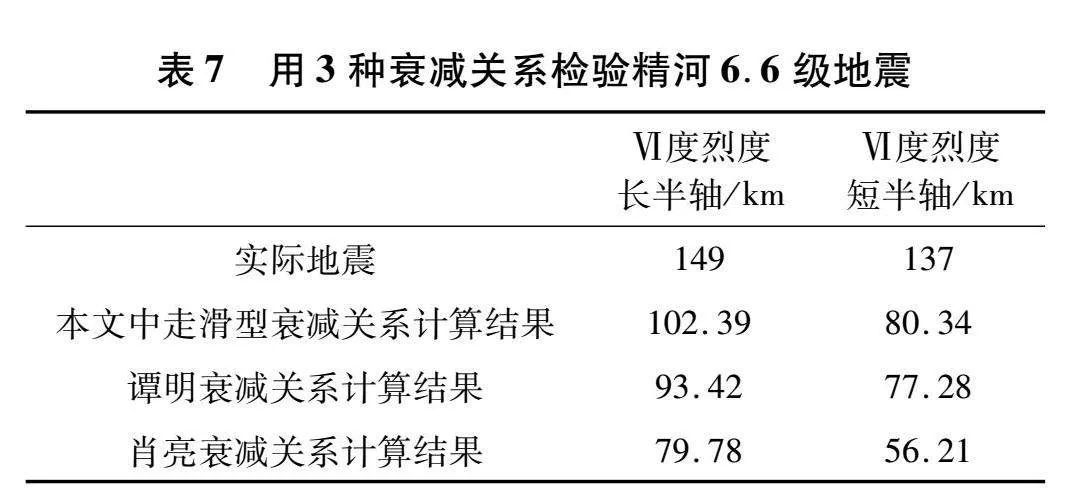
以2020年1月19日伽师6.4级地震来验证，此次地震震源破裂方式为逆断型，Ⅵ度烈度长半轴长度为135 km、短半轴长度为71 km，用3种衰减关系计算得到的结果对比见表6。以2017年8月9日精河6.6级地震来验证，此次地震震源破裂方式为走滑型，Ⅵ度烈度长半轴长度为149 km、短半轴长度为137 km，用3种衰减关系计算得到的结果对比见表7。对比两次地震发现，肖亮西部地区新疆地区烈度衰减关系得到的长、短半轴长度与实际地震烈度差异较大，而本文中衰减关系得到的长、短半轴长度和谭明衰减关系得到结果与实际地震烈度差异相对较小。相对而言，本文中两种模型烈度衰减关系得到的长、短半轴长度较谭明的衰减的关系更为接近实际烈度分布情况。

4 结束语

从新疆整体烈度衰减看，1716—1970年的烈度衰减关系曲线近场烈度比1970—2020年的近场烈度稍大，可能因为1970年前高震级烈度数据较多，低震级烈度数据有遗漏；当M=5或6时，1716—1970年的烈度衰减快于1970—2020年，说明1970年后MS≤7.0的地震烈度影响范围有扩大的趋势。发震方式对地震烈度衰减关系的影响较为显著。走滑型和逆断型烈度衰减有明显差异，近场范围内逆断型地震烈度大于走滑型，随距离的增加两者烈度逐渐接近；远场范围内长轴方向逆断型烈度衰减曲线衰减速度快于走滑型。总体来看，M=6或7时，走滑型地震的烈度衰减曲线值小于逆断型衰减曲线烈度值。长轴方向走滑型地震影响范围大于逆断型地震，但两者在短轴方向的影响范围差异不大。同一区域不同震源机制的地震烈度衰减特征有差别，不同区域相同震源机制的烈度衰减关系并不完全一致，震源机制对不同震级的烈度影响也不同。

本文中通过设定不同时间节点、不同震源机制解进行烈度衰减关系拟合，采用数学方法对新疆地区不同震源机制解的地震烈度衰减曲线进行头尾限定修正，更符合实际地震烈度衰减情况，可在新疆破坏性地震初评估中用以初步确定受灾范围。地震震源破裂性质不同的烈度衰减关系长短轴可作为地震灾害快速评估系统中烈度影响场的修正因子，在地震发生后及时得到震源机制解，修改和完善烈度圈长短轴数据。

参考文献：

［1］ 雷建成，高孟潭，俞言祥.四川及邻区地震动衰减关系［J］.地震学报，2007，29（5）：500-511.

［2］ 任静，李志强，徐志双.青海省地震烈度衰减关系研究［J］.中国地震，2020，36（3）：620-629.

［3］ 张齐，胡进军，谢礼立，等.地震动衰减关系区域性差异初步探讨［J］.地震工程与工程振，2018，38（4）：150-157.

［4］ 肖亮，俞言祥.中国西部地区地震烈度衰减关系［J］.震灾防御技术，2011，6（4）：358-371.

［5］ 谭明，李帅，孙静，等.新疆地震烈度衰减关系模型参数拟合［J］.内陆地震，2011，25（1）：29-35.

［6］ 冉慧敏，张志斌，赵庆.2012年6月30日新疆新源—和静MS6.6地震序列震源机制解［J］.中国地震，2014，30（3）：432-441.

［7］ 孙昭杰，李金.2019年10月27日乌什MS5.0和MS4.5地震震源机制解［J］.内陆地震，2019，33（4）：378-384.

［8］ 宋春燕，高荣，刘建明，等.2018年9月4日新疆伽师MS5.5地震序列及发震构造讨论［J］.中国地震，2019，35（2）：256-268.

［9］ 李艳永，王成虎，朱皓清，等.北天山地区震源机制与构造应力场特征［J］.地震，2020，40（2）：117-129.

［10］刘萍，魏芸芸，张琳琳.新疆皮山MS5.1、叶城MS5.0地震震源机制解分析［J］.内陆地震，2021，35（4）：301-308.

［11］龚固斌，冉慧敏，黄帅堂，等.2021年3月24日新疆拜城MS5.4地震震源机制解及发震构造探讨［J］.内陆地震，2022，36（2）：112-120.

［12］金花，李越帅，曹昌军，等.新疆南天山西段震源机制解与构造应力场特征分析［J］.内陆地震，2022，36（4）：329-337.

［13］郑韵，姜立新，杨天青，等.基于震源机制解的分区地震烈度衰减关系研究［J］.震灾防御技术，2016，11（2）：349-359.

［14］谢江丽，阿布都瓦里斯·阿布都瓦衣提，黄帅堂.柴达木-阿尔金地震带b值统计计算［J］.震灾防御技术，2022，17（1）：95-103.

［15］谢江丽，谭明.新疆破坏性地震综合等震线图的绘制与分析研究［J］.内陆地震，2015，29（2）：141-147.

［16］高国英，温和平，聂晓红.1991—2002年新疆中强震震源机制解分析［J］.地震，2005，25（1）：81-87.

［17］俞言祥，李山有，肖亮.为新区划图编制所建立的地震动衰减关系［J］.震灾防御技术，2013，8（1）：24-33.

［18］郁署君.确定烈度衰减关系的椭圆投影两步拟合法［J］.地震学报，1993，15（1）：109-144.

SEISMIC INTENSITY IN XINJIANG BASED ON FOCAL

MECHANISM SOLUTION RESEARCH ON

ATTENUATION RELATIONSHIP

XIE Jiang-li， Abuduwalisi Abuduwayiti， ZHANG Wen-xiu，LI Bo

（Earthquake Agency of Xinjiang Uygur Autonomous Region，Urumqi 830011，Xinjiang，China）

Abstract： Collect 130 destructive earthquake events with intensity data from 1716 to 2022， supplement the recent destructive earthquake intensity data in Xinjiang， and classify 124 seismic intensity maps and 281 pairs of intensity circle long and short axis data. The mathematical method is used to fit the seismic intensity attenuation model of different time nodes and different focal mechanisms in Xinjiang. It is found that in the process of intensity attenuation， strike-slip and reverse-fault earthquakes are slightly different. Different seismic source rupture properties will affect the long and short axes of intensity attenuation relationship. Therefore， we can use it as a correction factor to quickly evaluate the intensity influence field of earthquake disasters. After the earthquake occurs， the long and short axis data of the intensity circle can be modified and improved to evaluate more accurately.

Key words： Intensity；Seismic intensity attenuation relationship；Source mechanism solution；Earthquake disasters