我和正方形有个约会

新学期，学校新建了一个“数学活动俱乐部”，可以让喜欢数学的同学在里面尽情阅览数学读物，畅玩数学闯关游戏，甚至还可以把里面好玩的数学玩具借回家！

这个俱乐部可受大家的欢迎了！这不，今天，我、陆小豆、李嘉阳、王凡相约一起来到了这个奇妙的数学乐园。

11月5日 星期二

拼合的奥秘

“赵依茗，快来看这里装的是什么！”手快的陆小豆一进门就直奔数学玩具区，只见他拿着一个胖小猪，边招手边喊我过去看。原来，这个小猪形状的容器里装的是很多大大小小的正方形磁力片，有的边长1厘米，有的边长2厘米。

最近我们正好在复习三年级学的图形周长的相关知识，于是我迫不及待地出了道题考考陆小豆：“将3个边长都是1厘米的小正方形拼成一个长方形，它的周长是多少厘米？”

“这个简单哪，看我的！”只见他胸有成竹地拿出3个小正方形摆成一排，“我们可以先算出拼成的大长方形的长是3厘米，宽是1厘米，然后用（3＋1）×2算出周长是8厘米。”

听了他的回答，我又问他：“既然长方形是由3个同样的小正方形拼成的，那么它的周长和这3个正方形的周长之和相等吗？如果不相等，又是为什么呢？”

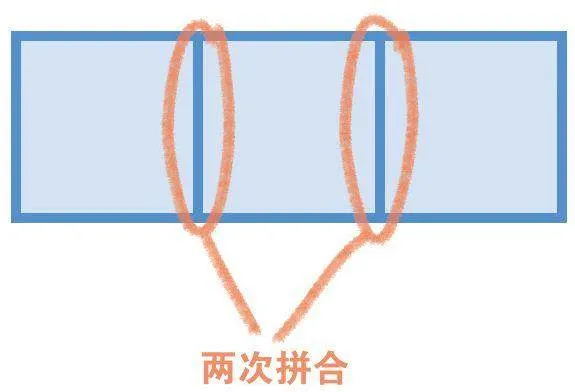
陆小豆凝神想了想说：“我们数一数就会发现，拼成的长方形周长只包含小正方形的8条边长，而原来3个小正方形的周长之和一共有12条边长，因为每两个小正方形拼合后中间就少了2条边长，这里一共有2次拼合，每条边长1厘米，所以一共少了4厘米，因此我们还可以用原来3个正方形的周长之和减去小正方形的4条边长，算出拼成的长方形周长，1×4×3－2×2＝8（厘米）。”

听了陆小豆的解释，我忍不住为他点赞，看来这个家伙学得不错呢！

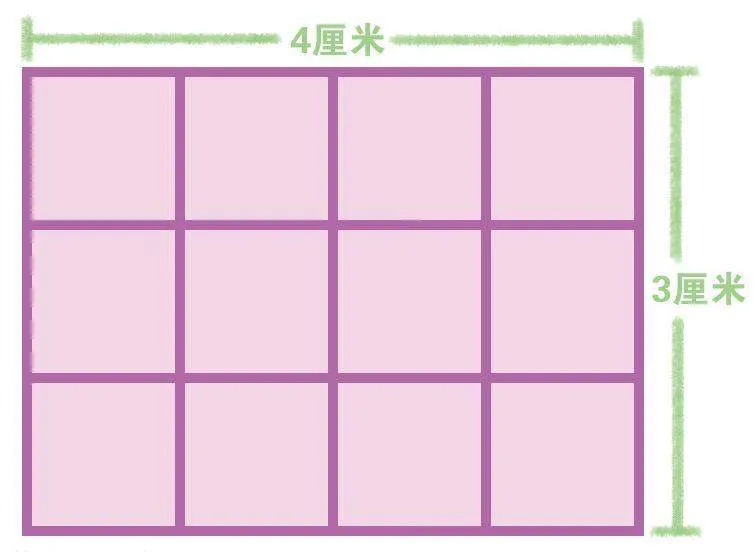
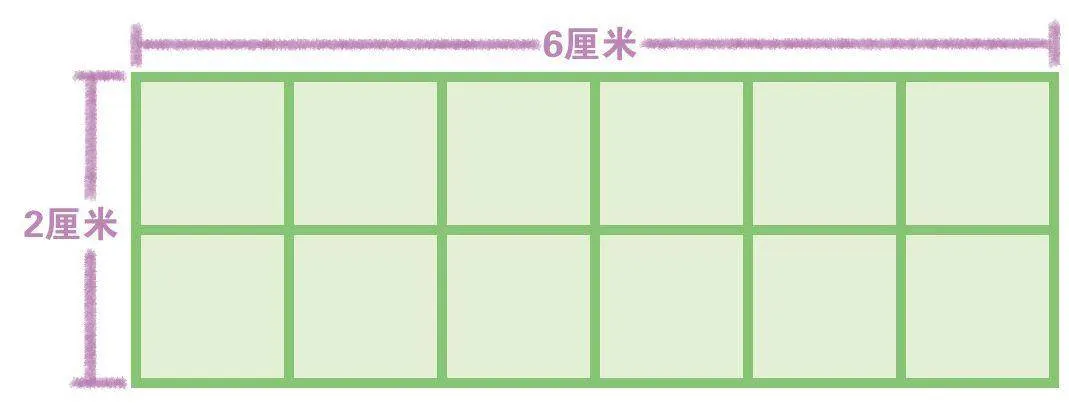
还没等我缓过神来，陆小豆出题考我了：“你来说说，用12个边长是1厘米的正方形可以拼成几种不同形状的长方形？哪一种周长最短？”这可难不倒我，我三下两下就用小正方形拼出了三种形状的长方形。对着相应的图，先分别求出这三个长方形的长和宽，然后根据周长公式算出它们的周长分别是（12＋1）×2＝26（厘米）、（6＋2）×2＝16（厘米）和（4＋3）×2＝14（厘米）。因此“每行拼4个，拼3行”这种长方形的周长最短。

我们在计算几个图形拼成的新图形周长时，一定要先拼一拼或者画一画，再根据图形找出所需的条件，运用周长公式进行计算，或者仔细观察拼图过程，思考减少的边数情况，灵活计算。

用一些相同的小正方形拼成长方形，形状可能不唯一，周长也不一定相等。当拼成的长方形的长和宽越接近，它的周长就越短；反之，当拼成的长方形的长和宽相差越大，它的周长就越长。

学有所用

1.用3个边长为2厘米的正方形拼成一个长方形，这个长方形的周长比3个小正方形的周长的和少了多少厘米？

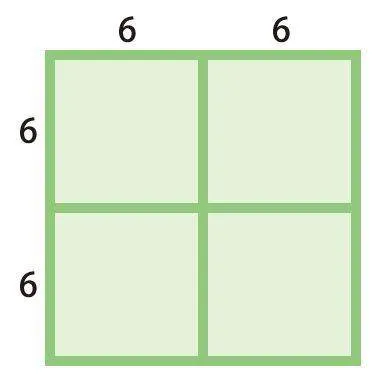
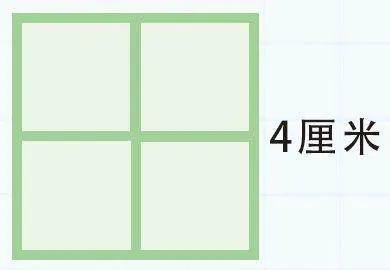
2.用4个边长为2厘米的正方形拼成一个大正方形，求这个大正方形的周长。

3.用18个边长为1厘米的正方形拼成一个周长最短的长方形，这个长方形的周长是多少厘米？

11月12日 星期二

巧分正方形

今天来到数学活动俱乐部，我被一个“巧分正方形”的闯关游戏深深吸引。

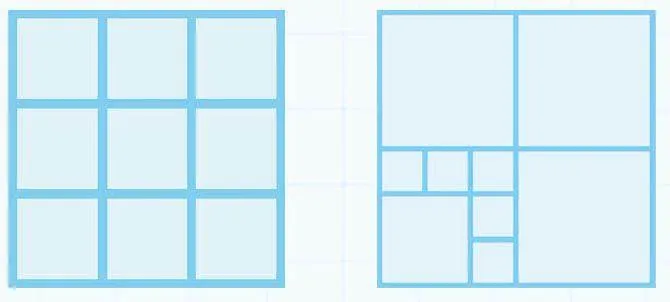
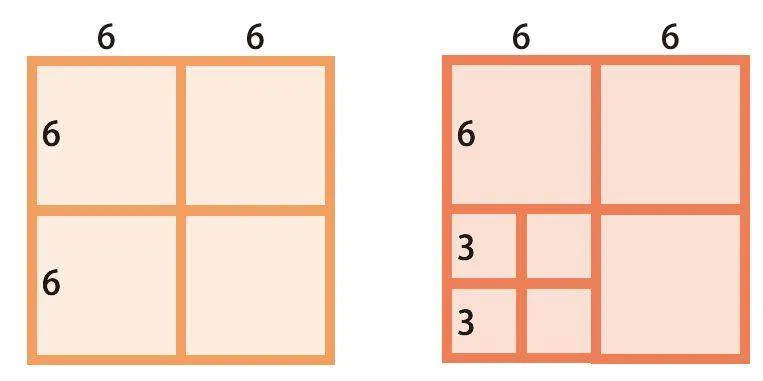
第一关超级简单：将一个边长是12厘米的正方形分成4个小正方形。我想都没想就居中画了一个“十字架”，这样就把正方形的边长分成了2份，整个大正方形就分成了4个小正方形。

谁知第二关就开始难了：将一个边长是12厘米的正方形分成6个小正方形。我在纸上比画来比画去，半天也没想出结果。没办法，忍不住偷看了旁边的智慧锦囊，原来，题目虽然要求分成6个小正方形，但这6个小正方形可以一样大也可以不一样大。因此我们可以先把边长平均分成3份，这样就可以分成9个相等的小正方形，然后再将其中4个相等的小正方形合并成一个较大的正方形，那么正方形的个数就会少掉3个，这样图中就一共只有6个小正方形了。

借助这个智慧锦囊，我又顺利地闯过了第三关：将一个边长是12厘米的正方形分成8个小正方形。我按刚才的思路，先把边长平均分成4份，这样就一共分成了16个相等的小正方形，然后将其中的9个小正方形合并成一个大一点的正方形，这样就一下子少掉了8个，16－8＝8（个），顺利完成任务。

就这样我闯入了第四关：将一个边长12厘米的正方形分成7个小正方形。我以为凭着刚才的办法，自己胜券在握，谁知想了半天此法居然无用。但我又不想再次打开锦囊，只想依靠自己的力量解答出来。于是我就想，前面都是先多分再合并的，现在我是不是可以转换一下思路，先分少一点，再接着继续分呢？果然，当我循着这条思路往下尝试时，奇迹真的出现了。看，我先把边长平均分成2份，这样就把正方形分成了4个相等的小正方形，然后我又把其中一个小正方形再次平均分成了4个更小的小正方形，这样就增加了3个，整个图就一共分成了7个小正方形，真是完美！

只要记住以上是如何把一个正方形分成6个、7个、8个小正方形的，再将其中任意一个正方形分成4个更小的正方形，就可以得到9个、10个、11个……反复用此方法，就能把一个正方形分成任意多个小正方形啦。

学有所用

1.将一个边长12厘米的正方形分成10个小正方形。

2.将一个边长16厘米的正方形分成11个小正方形。

3.将一个大正方形分割成9个小正方形，至少想出两种方法。

11月19日 星期二

灵活转化解难题

当我踏进俱乐部大门的时候，就知道来晚了，几乎每个项目前都有人站着了，看来喜欢思维探索的同学真不少啊！我在人群里看到了好哥们王凡，他很专注地在思考，根本顾不上搭理我。我又看到了陆小豆，这家伙今天似乎特别兴奋，一直在和赵依茗说个不停，我只好在旁边当个流动的观众。

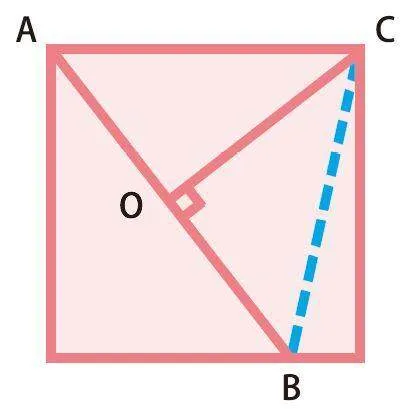
“李嘉阳，快来帮我一起想想！”原来是隔壁班的陈琪琪在叫我，我连忙转了过去。陈琪琪在看一本书，应该是遇到难题了。我一看，是一道图形题：一个正方形的边长是8厘米，AB＝10厘米，CO⊥AB，求CO的长。

读完题目我感觉似曾相识，想起在奥数社团里老师曾经讲过类似的题目，可以在图上添加一条辅助线来帮助解题。于是我试着把BC连起来，这样就形成了一个三角形ABC，而且这个三角形的面积正好是正方形面积的一半，8×8÷2＝32（平方厘米），AB是三角形的底，CO正好是这个三角形的高，32×2÷10＝6.4（厘米）。听了我的一番讲解，陈琪琪马上明白了。他热情地邀请我和他一起往下看，原来他看的题目全是和正方形有关的图形趣题。

很快，我们又看到了这样一道题：下图是由4个相同的直角三角形拼成的大正方形，如果三角形的直角边长分别是2厘米和3厘米，大正方形的面积是多少？

因为不知道大正方形的边长，我们就无法直接求出它的面积。所以我们需要转换一下思考的角度。通过观察，我们发现，这个大正方形是由4个相同的直角三角形和中间的一个小正方形组成的，而4个直角三角形的面积可以直接求出，3×2÷2×4＝12（平方厘米），中间小正方形的边长是3－2＝1（厘米），所以它的面积就是1×1＝1（平方厘米），大正方形的面积就是12＋1＝13（平方厘米）。

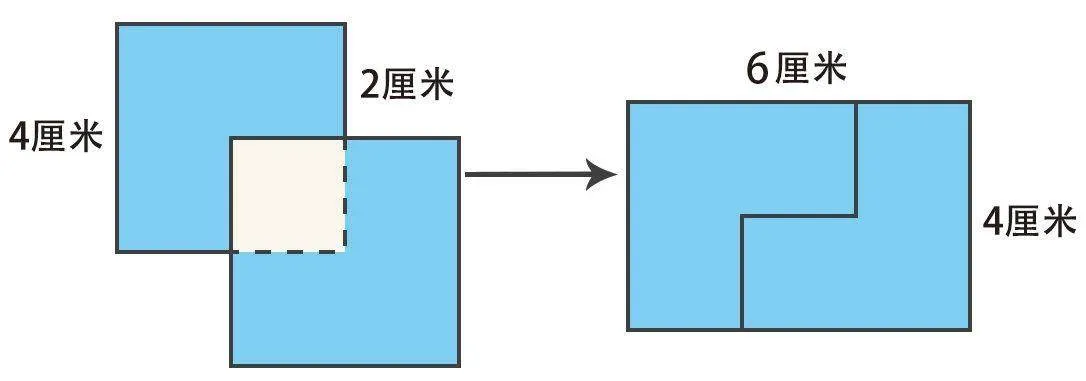
通过阅读，我们又知道了有时候可以借助平移、旋转等技巧，让图形运动起来，巧妙地求出阴影部分的面积。就如右图中右下方的大正方形可以向上平移2厘米，就形成了一个长方形，长是6厘米，宽是4厘米，阴影部分面积就是6×4＝24（平方厘米）。

解决这些和正方形有关的图形趣题，我们可以抓住图形的基本关系，灵活转换思路，虽然没有固定的模式，但我们可以用添加辅助线、拼拼移移、等量变换等灵活多样的形式，将未知变为已知，复杂转为简单，综合化成单一，顺利巧妙地解决这些难题。

真正用心去探索，时间就会过得特别快，收获满满的我们依依不舍地结束了与正方形的美好之约。小小正方形，美丽大世界，它还有很多有趣的数学问题等着我们去探索和发现，期待着再一次的美丽相约。

学有所用

1.求图中阴影部分的面积。（单位：厘米）

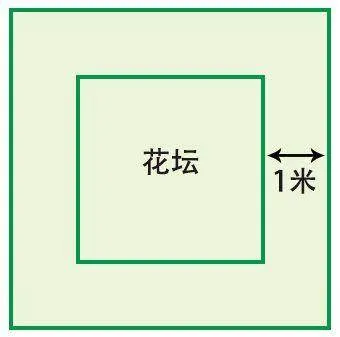
2.街心花园中一个正方形的花坛四周有1米宽的水泥路，如果水泥路的总面积是16平方米，那么这个花坛的面积是多少平方米？

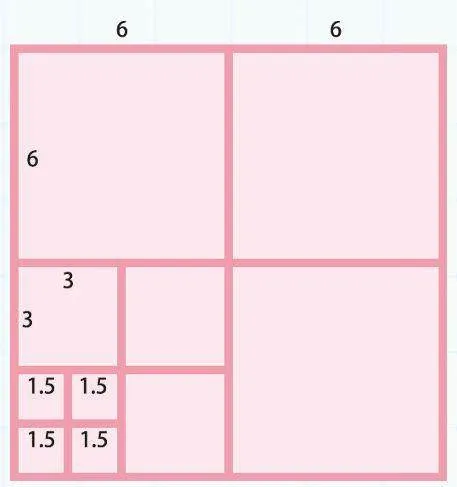
3.在大正方形纸里剪掉涂色部分，这3个涂色部分也都是正方形。已知涂色部分的周长是48厘米，则大正方形纸的面积是多少平方厘米？

演示过程

拼合的奥秘

1.用3个边长为2厘米的正方形拼成一个长方形，一共有2次拼合，少了4个边长，2×4＝8（厘米）。

2.拼成的大正方形的边长是4厘米，所以大正方形的周长是4×4＝16（厘米）。

3.用18个边长是1厘米的小正形拼成周长最短的长方形，长和宽应该最接近，所以长是6厘米，宽是3厘米，周长是（6＋3）×2＝18（厘米）。

巧分正方形

1.

2.

3.（答案不唯一）

灵活转化解难题

1.

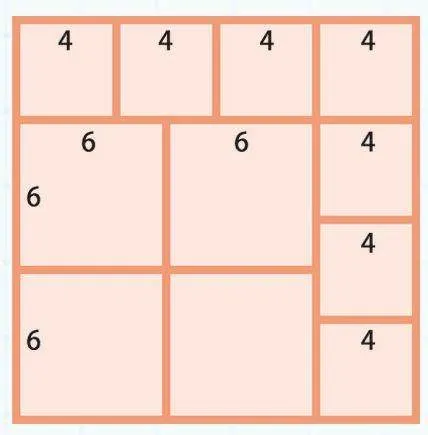
可以在右上角添补辅助线，让图形成为一个大长方形，然后用大长方形的面积减去左下角三角形的面积和右上角小长方形的面积。

大长方形面积：（4＋3）×4＝28（平方厘米）

小长方形面积：（4－3）×3＝3（平方厘米）

三角形面积：28÷2＝14（平方厘米）

阴影部分面积：28－3－14＝11（平方厘米）

2.可以把四周小路分割成几个相同的长方形、正方形进行思考。

方法一：16÷4＝4（平方米），4÷1＝4（米），4－1＝3（米），3×3＝9（平方米）

方法二：1×1＝1（平方米），1×4＝4（平方米），（16－4）÷4＝3（平方米），

3÷1＝3（米），3×3＝9（平方米）

答：这个花坛的面积是9平方米。

3.通过转化发现，涂色部分的周长正好和大正方形的周长相等。

48÷4＝12（厘米），12×12＝144（平方厘米）。

答：大正方形纸的面积是144平方厘米。