分月饼学数学:圆与扇形的趣味应用

今天是个特别的日子—中秋节！家里的气氛格外温馨，爷爷奶奶、爸爸妈妈都围坐在院子里，桌上摆满了各式各样的月饼，还有那轮明晃晃的大月亮挂在天边，像极了一个巨大的、发光的月饼。

这次爸爸买了很多种口味的月饼，有蛋黄的、莲蓉的、流心奶黄的、豆沙的，还有鲜肉的，我每一个都想尝尝，可惜没有那么大的肚量，只能一种吃一小块。大家都是这么想的，所以妈妈让我把月饼切一下，这样每个人就都可以多尝几种味道了。

我兴奋地想要立刻分给大家，但笨手笨脚的我完全不知道该怎么均匀地分。就在这时，我的学霸徽章突然闪烁—是学霸精灵出现了！

“小豆，需要帮忙吗？”学霸精灵温和地问道。

我点点头：“当然！我们家有6个人，怎么才能把这个大月饼分成大小完全一样的6份呢？”

学霸精灵用它那充满智慧的声音说：“陆小豆，这里有个教你关于圆形和扇形知识的好机会哦。”然后它和我解释了如何用数学的方式来公平地切分月饼。

它告诉我，整个月饼就是一个圆形，我们可以根据家人的数量来计算切割的扇形角度。我们家有6个人，那么就需要把圆形360°平均分成6份，每人就可以得到一个360°÷6＝60°的扇形月饼。

我用尺子和分度器小心翼翼地测量出了60°的角度，并在月饼上轻轻画下标记—虽然一开始有点紧张，但在学霸精灵的鼓励下，我觉得自己好像也能成为一个小小学霸！接着，我按照标记用刀切开了月饼，每个人都得到了均等的一份。妈妈还表扬了我，说我这次切得真专业！

爷爷笑着说：“小豆，今天你不仅学会了一点基本的几何知识，还把月饼分得这么公平，真棒！”我的心里美滋滋的，这个中秋节真是既有趣又有意义。

通过今天的事情，我发现数学真的是无处不在，它不只是课本上枯燥的题目，还是可以应用在我们的日常生活中。

在这个中秋之夜，我不仅收获了美味的月饼，更收获了知识的甜蜜。感谢学霸精灵，让我在快乐中成长，让数学变得不再枯燥乏味。

我抬头望向那轮明月，心中充满了感激和期待。明天，又会有什么新奇的知识等待着我去探索呢？

晚安，亲爱的日记本；晚安，中秋之夜。

陆小豆

难度：

已知一个扇形的圆心角为120°，半径为2，这个扇形的面积和周长各是多少？（π取3.14）

面积4—，周长8—

扇形的面积=—≈—

=—=4—；

周长=2r＋—≈2×2＋—

=4＋4—=8—。

难度：

如图，有8个半径为1厘米的小圆，用它们圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。如果圆周率π取3.14，那么花瓣图形的周长和面积分别是多少？

周长31.4厘米，面积19.14平方厘米

如图所示：

花瓣图形在正方形之外的部分是4个半径为1，圆心角为270°的扇形，每个扇形的弧长是相同半径的圆周长的—，那么它们的弧长之和是3个圆周长，即3×2πr≈3×2×3.14×1=18.84厘米；每个扇形的面积也是圆面积的—，则它们的面积之和也是圆面积的3倍，即3×πr²≈3×3.14×1²=9.42平方厘米。

花瓣图形的周长在正方形内的部分是4个半圆，它们的周长之和是圆周长的2倍，即2×2πr≈2×2×3.14×1=12.56厘米。

这4个半圆的面积之和也是圆面积的2倍，即2 ×πr²≈2×3.14×1²=6.28平方厘米。

因此花瓣图形的周长就是4个扇形的弧长与4个半圆的周长之和，即：18.84+12.56=31.4厘米。面积就是4个扇形的面积与正方形面积之和，再减去挖掉的4个半圆的面积，即9.42+4×4-6.28=16+3.14=19.14平方厘米。

难度：

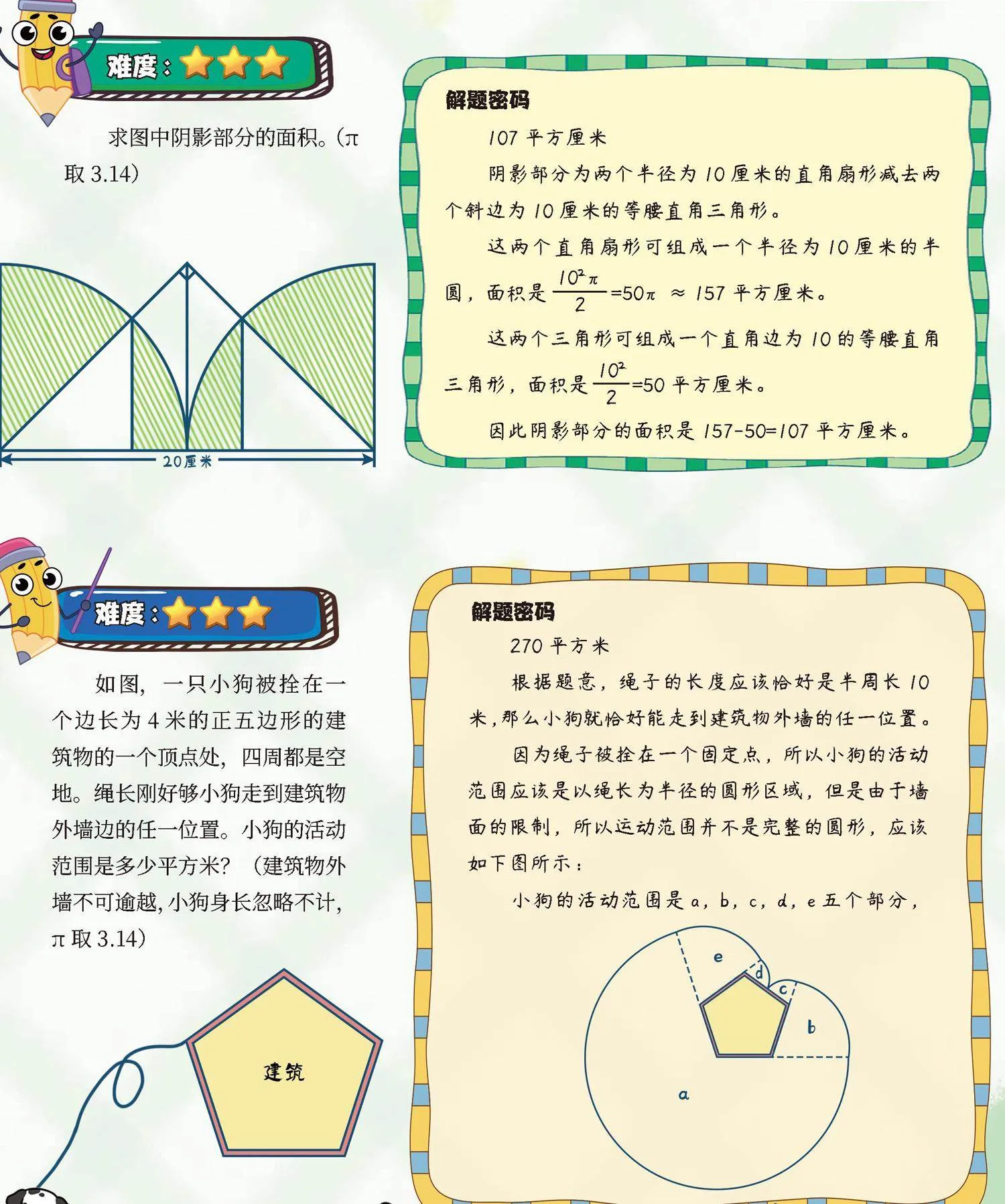
求图中阴影部分的面积。（π取3.14）

107平方厘米

阴影部分为两个半径为10厘米的直角扇形减去两个斜边为10厘米的等腰直角三角形。

这两个直角扇形可组成一个半径为10厘米的半圆，面积是—=50π≈157平方厘米。

这两个三角形可组成一个直角边为10的等腰直角三角形，面积是—=50平方厘米。

因此阴影部分的面积是157-50=107平方厘米。

难度：

如图，一只小狗被拴在一个边长为4米的正五边形的建筑物的一个顶点处，四周都是空地。绳长刚好够小狗走到建筑物外墙边的任一位置。小狗的活动范围是多少平方米？（建筑物外墙不可逾越，小狗身长忽略不计，π取3.14）

270平方米

根据题意，绳子的长度应该恰好是半周长10米，那么小狗就恰好能走到建筑物外墙的任一位置。

因为绳子被拴在一个固定点，所以小狗的活动范围应该是以绳长为半径的圆形区域，但是由于墙面的限制，所以运动范围并不是完整的圆形，应该如下图所示：

小狗的活动范围是a，b，c，d，e五个部分，都是扇形，其中b和e一样，c和d一样。

五边形的内角和是180°×（5-2）=540°，所以每个内角为540°÷5=108°。

其中a的半径是10米，圆心角为360°-108°=252°。

扇形b，e的半径是10-4=6米，圆心角为180°－108°=72°。

扇形c，d的半径是6-4=2米，圆心角也为72°。

所以活动范围的总面积为：

Sa+Sb+Sc+Sd+Se

=—×π×10²＋—×π×6²×2＋—×π×2²×2

=70π＋—π＋—π

=86π

≈270

小狗活动的范围是270平方米。

难度：

一个等边三角形边长为2厘米，以它的每个顶点为圆心，边长为半径分别作一段弧形成一个曲边三角形，如图。现在固定一个曲边三角形A，用另一个曲边三角形B围绕着它滚动。那么B滚动一周回到原来位置的过程中，扫过的面积是多少平方厘米？（π取 3.14）

25.12平方厘米

如下图，扫过的图形即为图中的阴影部分。

阴影部分可分成六小块。

其中有三块是扇形，可组成一个半径为2厘米的半圆，面积是—=6.28平方厘米；

剩下的三块可以组成半个圆环，外圆的半径是4厘米，内圆半径是2厘米，面积是—=18.84平方厘米。

整个阴影的面积是6.28+18.84=25.12平方厘米。

圆与扇形的应用

机器人学

在机器人学中，圆形和扇形被用来设计机器人的转动部件，使其能够精准地控制运动和方向。例如，旋转关节的设计往往参考圆形和扇形，从而实现复杂的机械运动。

天体物理学

天文学家使用圆形和扇形的概念来计算天体的轨道，以及分析由望远镜捕获的星体图像。通过这些计算，科学家能够预测星体位置，以及探索宇宙的奥秘。

计算机图形学

在这个领域，圆形和扇形被用来生成图形界面中的各种图形和动画。通过对这些基本形状的操作，程序员和设计师能够营造出各种视觉效果。

人工智能与机器视觉

在进行图像识别时，圆形和扇形的数学模型常被用来检测和识别图像中的特定形状，例如，自动识别道路标志或者是进行面部识别。

通信技术

无线电波的传播模型中常常用到圆形和扇形的概念。信号从一个点发射时，其覆盖的区域可以用圆形来表示，而定向传播则可能采用扇形模型来优化信号的分布。