漫话三角形

一、三角形是最基本的多边形

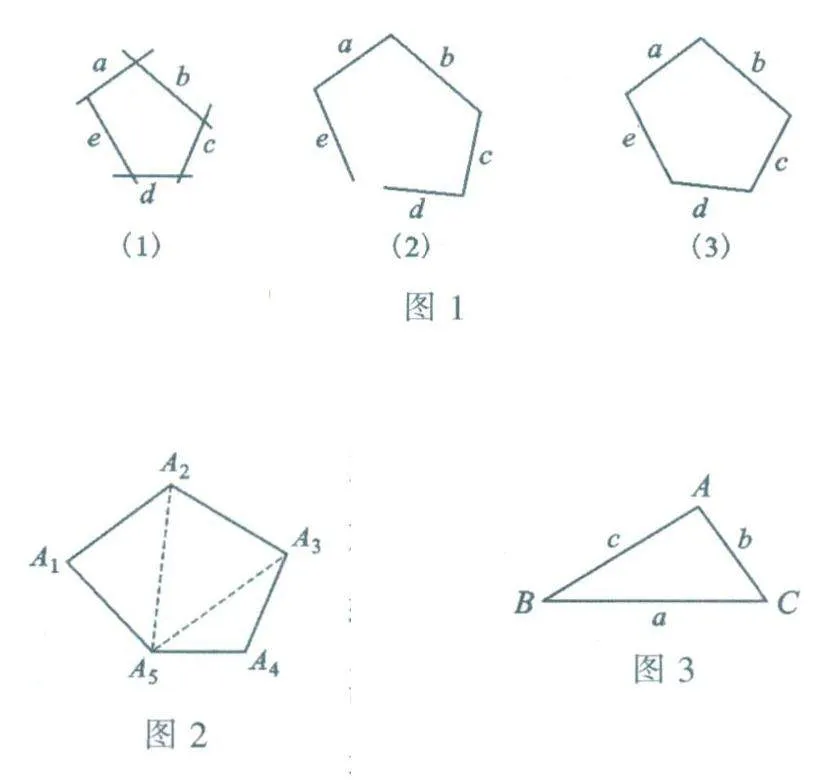
由若干条线段依次首尾相接，并且相接的两条线段不在同一直线上，这样围成的封闭图形叫作多边形.图1中的三个图形都由z，b，c，d，e这5条线段组成，其中（1）（2）都不是多边形，只有（3）符合多边形的定义，漫话三角形

由n（n≥3）条线段组成的多边形，叫作n边形.由不在同一直线上的三条线段首尾顺次相接所组成的封闭图形叫作三角形，三角形是边数最少的多边形，因此是形状最简单的多边形.当n≥4时，n边形都可以分解为若干个三角形，如图2.这就是说，多边形的问题可以转化为三角形的问题来解决.因此，三角形可以看作最基本的多边形，研究三角形是认识多边形的第一步.

三角形有三条边和三个角，它们是三角形的6个基本元素.下面重点讨论三角形的边和角.

二、三角形的边

组成三角形的三条线段，叫作三角形的边，它们分别在三条不同的直线上，连接每两条边的点，叫作三角形的顶点，图3中的三角形通常按它的顶点顺序记作△ABC.线段AB.BC.CA是它的三条边，通常也按各边所对的顶点分别把它们记作c，a，b.

任选三根小木棍首尾相接一定能搭成三角形吗？观察图3.连接点曰和点C的连线有线段BC和折线BAC.因为两点之间线段最短，所以折线BAC比线段BC长，即AB+A C>BC，也即c+6>a.由此可知，三角形的任意两边之和大于第三边.这是三角形三边之间的基本数量关系，如果三根小木棍中任意两根合起来都比另一根长，则它们首尾相接能搭成三角形：否则不能.

设a，b，c是三角形的三边，则a

三角形的三边长可以各不相等，也可以有相等的边，三边长都不相等的三角形，叫作不等边三角形.有相等的边的三角形，叫作等腰三角形，其中相等的边叫作腰.等腰三角形中还有更特殊的一种，即三边都相等的三角形，它叫作等边三角形，

一个多边形的形状和大小是由它的各个顶点的相对位置决定的.一旦这些顶点相互之间的位置确定了，多边形就随之确定了.已知三角形的三边长，则三个顶点的相对位置就确定了，因此三角形就确定了.做试验：用三根木条钉成一个三角形后，扭动木条，可以发现不能改变三角形的形状和大小.这就是三角形特有的稳定性，人们在实践活动中经常利用这个性质，然而，对于四边形、五边形等多边形，如果仅仅已知它们各边的长度，则并不能确定这些多边形的形状和大小.做试验：用四根木条钉成一个四边形后，扭动木条，可以发现虽然各边长度不变，但能改变四边形的形状和大小.在多边形中，只有三角形可以由各边长确定图形的形状和大小，

三、三角形的角

多边形相邻两边所夹的角叫作多边形的内角，简称多边形的角.三角形有三个角，三角形的三条边确定后，三角形的三个角随之确定，反过来，三角形的三个角确定后，三角形的三边长并不能确定.例如，请几个同学分别画出三个角都等于60°的三角形，画出的三角形虽然形状相同但很可能大小不等，从这个意义上说，三角形的边对图形整体的影响要大于角.

小学时大家已经通过度量角度和折纸等实验方法，看到“三角形三个内角的和等于180°”，但是，这些实验都是针对具体的三角形进行的.对实验过的三角形成立的结论，对所有三角形都成立吗？因此，我们必须找到一种不依赖于具体的三角形，而适合一般的三角形的非实验的研究方法，这就是逻辑推理.实验方法只是验证，由它只能对有限的特殊对象作出判断；逻辑推理方法是证明，由它得出的是适合整体的、一般的对象的结论，在数学中，逻辑推理是占重要地位的方法，

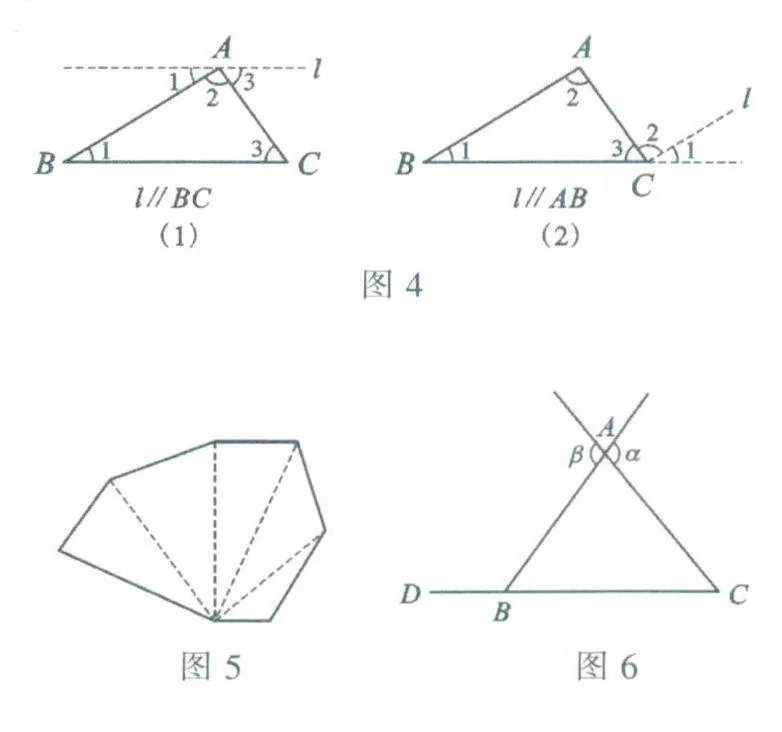
对任意三角形，要证明“三个内角的和等于1800'’，很容易想到，如果能推导出这三个角合起来恰好等于一个平角，那么结论就成立了.如图4，△ABC中，∠1，∠2，∠3三个内角的顶点是分离的，怎样把它们搬到一起呢？大家已经学习了平行线的知识，知道“两直线平行，内错角相等，同位角相等”等结论，由此很可能会想到利用平行线来“搬角”，图4所示的两种证法就是这样想出来的，图中的虚线是为完成证明所添加的辅助线，它使要证的三个角严丝合缝地拼在一起，成为一个平角，从而证明了三角形三个内角的和等于1800.图4中的△ABC可代表任何一个三角形，这种推理不依赖于对具体三角形进行实验，而对所有三角形都适合.因此，经推理所得的结论具有普遍性，它被称为三角形内角和定理.

如图5，n边形可分解为n，-2个三角形，于是由三角形内角和等于1800，可推出n边形的内角和等于（n-2）.180°.这个结论是建立在三角形内角和定理上的一个推论.由此也可以看出，研究三角形是研究多边形的基础，

三角形的一边与另一边的延长线所组成的角，叫作三角形的外角.如图6，∠ABD是△ABC在顶点B处的一个外角.三角形的内角与和它相邻的外角互为邻补角.在三角形的每个顶点处都有两个外角，它们是对顶角，如图6中的α和β，

在△ABC的每个顶点处各取一个外角，它们的和叫作△ABC的外角和.△ABC的外角和等于（180°∠A）+（180°-∠B）+（180°一∠C）=540°-（∠A+∠B+∠C）=540°-1800=3600°.

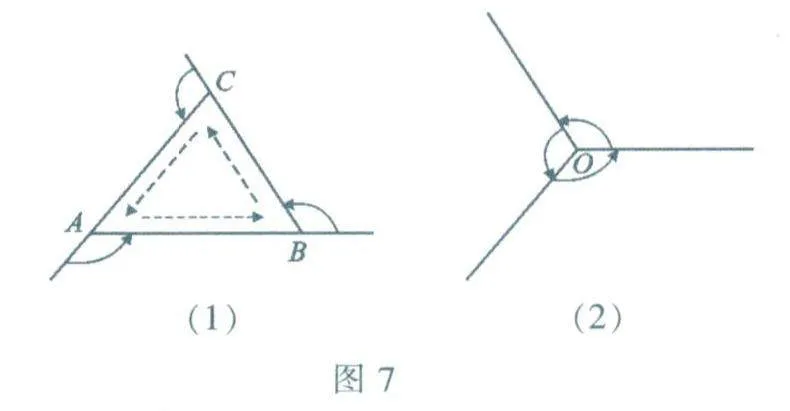
我们还可以用另一种方法考虑三角形的外角和.如图7（1），假设一个人开始站在点A处，面向点B，他沿AB边走到点B，又沿BC边走到点C，再沿CA边走到点A，并且转身面向点B.在此过程中，他在点A，B，C处各转了一个角度，这三个角度正好等于三角形的三个外角.他走了一周最后仍是站在点A面向点B，恢复到开始时的站法，从转动角度看，相当于他转了一个周角.如图7（2），将三次转动的角移到同一顶点O的位置，更容易看出所转各角之和等于周角，即360°.

由三角形内角和定理可知，三角形中至多有一个钝角或直角.三角形可以按角分为三类：锐角三角形、直角三角形和钝角三角形，可以看出，这是以三角形中最大角的种类为标准划分的.每个三角形都属于这三类之一.而且只属于其中一类.这说明这样的分类满足“不重不漏”的科学分类要求.

不同类型的三角形除具有三角形共有的性质外，还有各自的特性，例如，锐角三角形各边上的高交于三角形内一点，直角三角形各边上的高交于三角形的直角顶点，钝角三角形各边上的高所在的直线交于三角形外一点.

一些有关三角形的问题，需要对不同类型的三角形分类讨论.

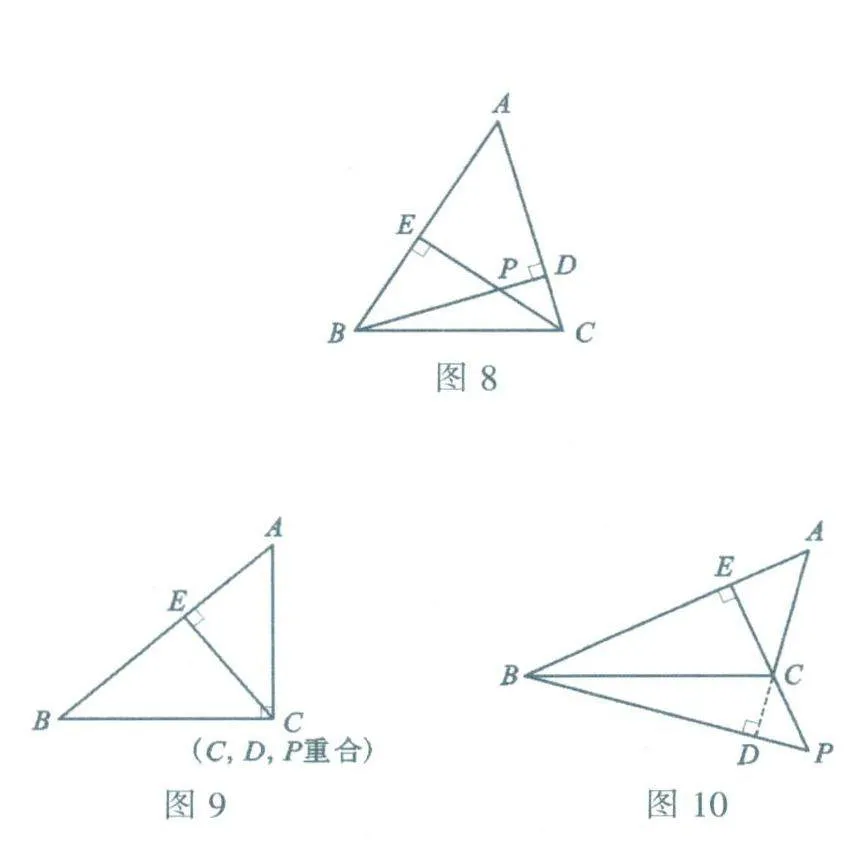
例 △ABC中，∠A=50°，两条高BD与CE所在的直线相交于点P，求∠BPC.

解：（1）如果△ABC是锐角三角形，那么点P在△ABC内部.如图8.易求得∠BPC=130°.

（2）如果△ABC是直角三角形，因为∠A =50°，所以∠B或∠C是直角，不妨设∠C是直角.如图9，此时∠BPC不存在.

（3）如果△ABC是钝角三角形，那么点P在△ABC外部，如图10.易求得∠BPC=500.

综上，∠BPC为130°或50°.