活跃思维，启发思考

“向量的加法运算”选自高一数学必修第二册（A版）（人教版）第六章“平面向量及其应用”。此课围绕向量的加法法则、向量的加法运算律展开，一般在1课时内可完成教学任务。课程教学内容属于向量的线性运算教学内容的基础，对于学生日后学习向量的减法运算等有奠基作用。

一、教材分析

“向量的加法运算”位于人教版高一数学必修第二册第六章，上承“向量”，下启“向量的数乘”“向量的分解与坐标表示”，在章节内起到了承上启下的重要作用。此节以向量加法的三角形法则、平行四边形法则以及向量加法的运算律为教学重点，包括矢量计算与作图等多种教学内容。

二、学情分析

“向量的加法运算”教学之前，学生完成了“向量”的学习，已掌握了向量的概念，初步认识了向量的方向性。同时，学生在物理课程中学习了力、速度等矢量的正交分解概念，有一定的知识基础。此外，高一学生具备一定的数学观察、数学抽象能力，能够基于生活实例对向量加法形成感性认识，体会向量的加法运算与数量的加法的区别。但是，受知识水平限制，学生难以系统描述两种加法运算的差异，无法解决向量的加法运算及实际应用问题。

三、课标分析

《普通高中数学课程标准（2017年版2020年修订）》（以下简称“新课标”）将“向量的加法运算”划入“几何与代数”教学模块，要求此课能够发展学生几何直观思维，提升学生代数运算能力，倡导教师渗透数形结合思想，指导学生感悟“数”与“形”的内在联系，提升学生的数学学科核心素养。

四、教学目标

1.明确向量加法的几何与代数意义，提升数学抽象素养。

2.学会用代数公式表示“向量加”，理解平行四边形法则、三角形法则，提升逻辑推理素养。

3.掌握基本的向量加法运算律，学会用运算律进行简便运算，提升数学运算素养。

4.经历向量加法运算法则推理的全过程，学会应用相关知识解决具体问题，提升逻辑推理与数学应用素养。

五、教学过程

本课结合使用情境教学法、对话教学法与探究教学法，辅以PPT出示图片，展示向量加法的几何表示，加深学生的直观认识。

（一）设计情境，引发兴趣

（多媒体播放Flash动画）

情境1：春节将至，张先生在S市工作，没有买到回老家A市的直达高铁，于是先后买了S市→B市、B市→A市的高铁。张先生两次位移的和是什么？

情境2：张先生的汽车在半路抛锚，打电话叫来两辆拖车。已知两辆拖车的牵引力都为1500 N，牵绳之间的夹角为55°。如果只要一辆拖车来牵引，要保证产生的拖拽效果与原来相同，这辆拖车的牵引力应当为多少N，它的行驶方向是什么？

（设计意图：选取生活实例同时应用动画演绎，加深学生的直观认识。同时，情境内容设在学生的“最近发展区”中，可以激活学生的思维，引导其用已掌握的位移、力的合成等矢量计算知识探究新问题，驱动学生对向量加法概念形成感性认识，为学生突破向量加法课程难点奠定基础。）

（二）设计问题，启发思考

设计连串问题链，驱动学生进阶思考。

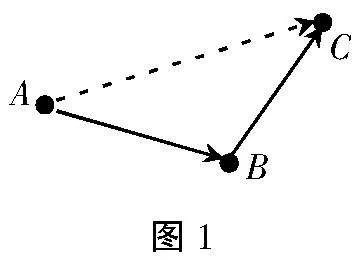
问题1：如图1所示，某质点从点A经过点B到点C，这个质点的位移怎么表示？

生1：该质点经过点B到点C，有两段位移，但实际移动距离是点A到点C的直线距离，因此该质点的位移应用点A到点C的距离表示。

（设计意图：引导学生从运算的角度出发，将质点位移问题转化为向量的加法运算问题，引导学生对向量的加法运算形成感性认识，同时在观察、讨论的过程中发现向量加法的三角形法则。）

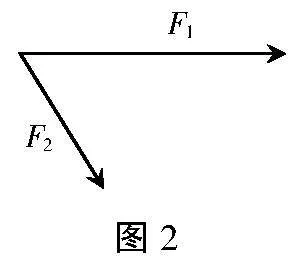
问题2：如图2所示，某物体受到F1，F2的作用，则该物体所受合力怎么求？

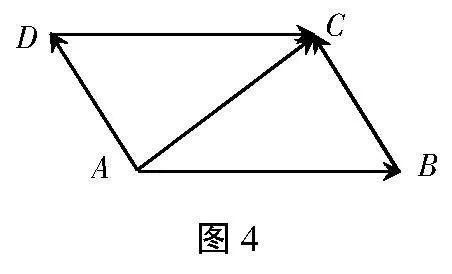
生3：从物理学的角度看，力的合成遵循平行四边形法则，如图3所示。

（设计意图：借助物理学力的合成问题引导学生回顾平行四边形法则，使学生基于自身知识储备迁移向量加法的平行四边形法则，得到运算规律，提高学生的数学观察、迁移类比、逻辑推理能力。）

问题3：向量加法中，平行四边形法则与三角形法则一致吗？为什么？

生5：两个运算法则都能用于求不同向量的和。

师：两个运算法则的使用条件相同吗？它们的用途、用法有哪些异同点呢？

生6：两个法则的使用条件不同。计算任意两个非零向量的和时，可以用三角形法则；计算两个不共线向量的和时，可以使用三角形法则，也可以使用平行四边形法则。

（设计意图：借助问题引导学生对比与分析，使学生在结合图示的过程中反思三角形法则、平行四边形法则的异同点，巩固学生学习所得，同时提高学生的数学思维水平。）

（三）设计活动，驱动探究

教学活动以探究活动为主，要富有层次性，旨在驱动学生在动手操作、动脑思考的过程中总结向量的加法运算规律。

探究活动2：数的加法满足交换律、结合律，向量的加法运算是否也满足交换律与结合律呢？展开讨论。

（用PPT出示图5，指导学生合作探究）

（四）设计练习，检测成果

练习以教科书、配套练习册内容为主，用以检测学生对向量的加法运算法则、运算律等知识的掌握与应用情况。

A.四边形ABCD是矩形

B.四边形ABCD是菱形

C.四边形ABCD是正方形

D.四边形ABCD是平行四边形

（设计意图：三道题均为基础题目，依次考查学生对向量的加法运算的运算法则、数学规律等知识的掌握情况。通过设计练习题巩固学生“向量的加法运算”学习基础，指导学生在解决问题的过程中感悟向量运算中蕴含的数学思想与方法，进一步提高学生的数学学科核心素养。）

六、作业设计

以书面作业为主，讨论作业为辅。其中，书面作业要求所有学生都要完成，讨论作业要求学有余力的学生完成。

书面作业：完成教科书P10练习题，P12的第1、2、3小题。

讨论作业要提升一点难度，略。

（设计意图：通过设计两个层次的作业巩固学生课上所学，又为学有余力的学生提供了自由发展的空间，进一步培养学生的创新意识与探索精神，同时为学生学习下节课内容做好准备。）

七、教学反思

此节教学设计环节严谨，按照学生认知发展特征设计了“情境导入→问题讨论→活动探究→课上检测”教学活动，逐步引导学生参与数学课堂，加深学生对“向量的加法运算”中平行四边形法则、三角形法则及运算律的学习体会。此外，作业设计以“分层教学”理念为指导，满足不同层次学生课后学习需要。总体来说，此教学设计有以下亮点：

第一，目标体现核心素养，指导学生进阶提升。教师要参考新课标确定高中学生发展需要，设计以推理能力、抽象能力、几何直观等核心素养为导向的教学目标，用于指导学生挖掘数学问题、探究活动中潜藏的知识，积累观察、分析、运算经验，提升数学核心技能。

第二，教学方式灵活多变，优化学生学习体验。此教学设计结合使用了情境教学法、讨论教学法与探究教学法，指导教师随时与学生展开师生互动，使学生在参与情境、分析问题的过程中主动发现数学问题，研究数学规律，抽象数学原理。

第三，教学内容丰富多彩，完善学生知识体系。教学设计给出了大量的向量的加法运算示意图、运算例题等，为学生进行数学观察、运算学习提供了资源支持，进一步增强了学生对“向量的加法运算”教学内容的感性认识与理性认知。