基于层次分析法的建筑施工测量课程评价体系研究

摘要：随着建筑施工测量课程的教学改革不断推进，构建合理的评价体系来评估学生的能力素养非常重要。本研究运用层次分析法（AHP）构建了建筑施工测量课程综合成绩评价模型，对考勤、课后拓展学习、课前及课后作业、课堂活动、课内实践考核、期末考试及考证八个因素进行了综合评估。通过对建筑工程技术专业学生的问卷调查数据分析，确定了各指标因素的相对权重。结果表明，课内实践考核、期末考试及考证三个因素对学生综合成绩评价有较高的影响权重。基于层次分析法分析结果，本文提出了促进建筑施工测量课程教学改革和注重培养学生实践能力和适应岗位综合能力的建议。

关键词：建筑施工测量课程；评价体系；层次分析法；人才培养

1概述

建筑施工测量课程是建筑工程技术专业的必修专业基础课，旨在与建筑工程技术专业人才培养目标对接，培养学生适应建筑工程测量员等工作岗位的能力。学生将通过该课程掌握工程测量的基本理论和实际操作技能，为未来在建筑工程领域的职业发展打下坚实的基础。

20世纪70年代初，ThomasL.Saaty提出了层次分析法（AHP）的决策分析方法。层次分析法（AHP）是一种多层次、多目标的方法，用于确定各个因素在整个层次结构中的相对重要程度。它通过进行两两比较来建立多层次结构，并结合主观判断和科学计算，给出备选方案的优劣顺序。层次分析法（AHP）能够将经验判断定量化，并将定性分析与定量分析相结合，为复杂的决策问题提供简洁高效的解决方法[1-2]。近年来，层次分析法（AHP）被广泛应用于教育领域，包括课程的教学质量评价、学生学习能力评价以及实践技能应用评价等。研究者们从多个角度对课程的教育体系进行了量化研究，为提高课程的教学质量提供了理论指导，这些研究为教育界提供了实用的工具和方法，并且在不同领域的评价中取得了显著的成果[3-8]。

随着建筑施工测量课程改革的推进，科学构建合理的评价体系以评估学生的知识掌握和能力水平已成为必然趋势。建筑施工测量课程的评价体系通常包含课堂表现、课后拓展、考试成绩等方面。然而，这些指标往往没有统一的权重分配，缺乏科学性和客观性。因此，本研究将基于层次分析法（AHP）应用于建筑施工测量课程的成绩评价体系，通过构建层次结构和两两比较矩阵，将评价指标进行权重分配和排序。通过学对建筑工程技术专业学生的问卷调查数据分析，评估学生在建筑施工测量课程中的学习情况和能力水平。

2构建建筑施工测量课程成绩评价模型

2.1设计层次结构模型

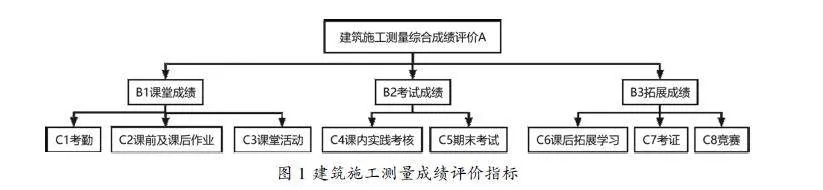
针对建筑施工测量课程的综合评价体系，本文使用层次分析法，对建筑施工测量课程的综合评价体系进行了划分，包括目标层、准则层和指标层。目标层为综合成绩评价，准则层包括课堂成绩、考试成绩和拓展成绩，指标层包括具体的评价指标：考勤、课后拓展学习、课前及课后作业、课堂活动、课内实践考核、期末考试及考证。

在课堂成绩方面，包括平时考勤、课前课后作业及课堂活动。平时考勤是通过签到等方式对学生的出勤情况进行定量评价，可以利用职教云平台进行。课前及课后作业是评估学生对课堂知识的预习和巩固情况的重要手段。课堂活动包括课堂测验、课堂讨论及课堂提问等。

考试成绩方面，包括课内实践考核和期末考试，期末考试是对整个学期知识的综合考核，可以利用在线平台随机组题进行综合期末测试。而课内实践考核可以帮助学生将理论知识应用到实际操作中，培养学生的实践能力，通过实践考核，学生可以学会运用所学知识解决建筑施工测量放样的实际问题，提高实际操作技能和解决实际问题的能力。

拓展成绩方面，包括课后拓展学习、考取测量相关证书及参加技能竞赛。课后拓展学习可以是在线职教云视频资源的观看等，帮助学生进行自主学习和拓展学习。测量相关证书包括1+X职业技能证书、岗位测量员证书等，可以激发学生学习主动性和学习热情。竞赛包括学校建筑技能节竞赛和全国职业院校技能大赛测量赛项等，这有助于培养学生的岗位素养。

通过构建这样的层次结构模型，我们能够更全面客观地评价学生在建筑施工测量课程中的学习情况和能力水平，为教师提供指导改进教学和学生发展的依据。

2.2确定各层次的权重系数

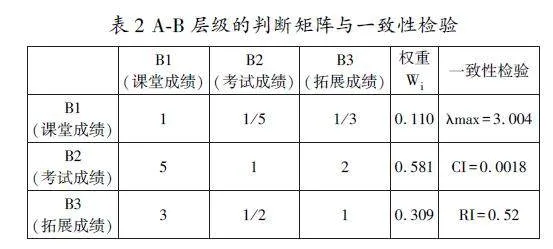
通过两两比较方法构造判断矩阵阵G=（aij）n×n，将各指标因素进行两两比较，使用1-9标度法来表示前一个因素与后一个因素相比的重要性程度，如表1所示。

其中，1表示前一个因素与后一个因素重要性相同，3表示前一个因素相比于后一个因素稍微重要，5表示前一个因素相比于后一个因素明显重要，9表示前一个因素相比于后一个因素极其重要，2、4、6、8来表示相邻重要性等级之间的量化指标。对于前一个因素不如后一个因素重要的情况，可以采用1-9的倒数来表示。

针对柳州铁道职业技术学院建筑工程技术专业建筑施工测量课程的160名学生，进行“建筑施工测量课程成绩综合评价”的问卷调查。对调查数据进行预处理，采用均值的方式进行调整，确保在评分上不存在较大的差异。

（1）准则层权重系数的计算

判断矩阵各元素的结果如表1所示。

对判断矩阵A按列进行归一化计算，得到：

求得两两比较判断矩阵A的特征向量：

元素Wi就是相应因素在层次单排序中的权重值。得到层次单排序中的权重值后，需要对判断矩阵进行一致性检验，根据上述公式计算及查表，首先计算判断矩阵A的特征向量的最大值：

则其一致性指标：

当判断矩阵阶数n=3时，RI=0.52，随机一致性比率，小于0.1，一致性检验通过。准则层对于目标层A的权重为（B1，B2，B3）=（0.110，0.581，0.309）。

（2）指标层的权重计算

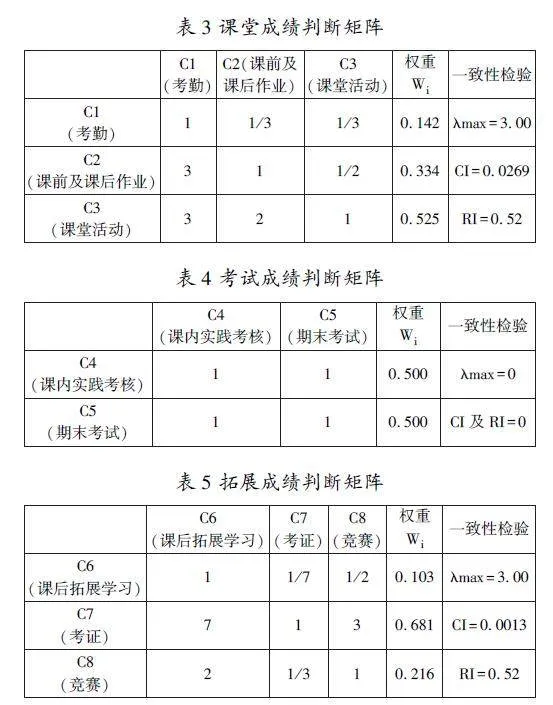
对于建筑施工测量课程的教学评价体系中指标层的各个指标，我们采用与准则层相似的计算步骤来构建判断矩阵，并计算它们的权重，并进行一致性检验。课堂成绩、拓展成绩和考试成绩的判断矩阵的相关信息可以见表2、表3及表4。

从表1表2及表3计算得到课堂成绩、拓展成绩及考试成绩指标层三个判断矩阵的一致性比率CR分别为0.0517、0及0.0025，都小于0.1，可认为上述三个特征向量的权重矩阵为：

（3）层次总排序及一致性检验

设，ai为A-B层级的判断矩阵所对应的因素i的权重，与bij相乘，即可求出A-C层级的各因素j对应的权重Cj，计算出层次总排序即指标层C1，C2，C3…，C8相对于目标层A的权重为（C1，C2，C3…，C8）=（0.02，0.04，0.06，0.29，0.29，0.03，0.21，0.07）。同时计算出组合一致性指标为CR小于0.1，一致性检验通过。

3建筑施工测量课程教学提出改进措施

根据对建筑施工测量课程综合评价体系的分析，发现课内实践考核、期末考试以及考证（如1+X职业技能证书和岗位测量员证书等）这三个因素在评价中具有较高的权重。这意味着教学工作需要在这三个方面进行重点加强和关注。课内实践考核可以提供学生在实际操作中的能力表现，期末考试则能够全面评估学生对建筑施工测量知识的掌握程度。而获得相关考证则证明了学生具备了一定的职业技能，能够更好地适应实际工作岗位的要求。因此，针对这些重要因素的加强将有助于提高教学质量和培养学生的综合能力。

在课内实践考核方面，教师可以采用小组讨论、实际操作演示等教学方法，引导学生将理论知识应用到实际工程测量的实践中。通过模拟实际测量任务和实际工程场景的训练，学生可以加深对理论知识的理解，并培养实际操作技能和解决实际问题的能力。同时，教师应当及时给予学生指导和反馈，帮助他们纠正错误并提高操作水平。

对于期末考试，它在学生学习和学业发展中具有重要的地位和作用。通过期末考试的过程，学生可以全面评估自身的学习水平、复习巩固知识、提高学习动力，并为未来的学习和发展奠定基础。在平时教学过程中，要强调期末考试的重要性。向学生明确解释期末考试对于学业发展和未来的影响，例如升学、就业等方面。让他们认识到期末考试不仅是一个评估学习成绩的机会，更是展示自己能力和知识掌握的重要时刻。同时，提供明确的考试目标和标准。向学生详细阐述期末考试的考试内容、考试标准和评分方式。让他们清楚知道应该达到的学习目标，以及如何以高标准去评估自己的学习成果。

对于技能考证，证书对于学生个人来说，具有提升就业竞争力、拓展职业发展机会、证明职业能力的作用。在平时教学过程中，解释技能考证的价值和作用。向学生详细解释技能考证对个人职业发展的重要性，包括提升就业竞争力、拓展职业发展机会、证明职业能力等方面的作用。让他们认识到持有技能证书的价值。介绍当前就业市场对于特定技能的需求和趋势。向学生展示技能考证与行业行情的对应关系。让他们明确技能证书在具体行业中的重要性和影响力。

通过以上改进措施的实施，可以提升建筑施工测量课程的教学效果。并培养学生的实践能力及适应岗位需求的综合能力。为他们未来的工程实践奠定坚实的基础。

结语

本文基于层次分析法（AHP）对建筑施工测量课程进行了综合评价分析，得到了影响综合评价的八个因素的权重排序（从低到高）：考勤、课后拓展学习、课前及课后作业、课堂活动、课内实践考核、期末考试及考证。其中，期末考试、考证及课内实践考核被认为是最重要的三个因素，它们特别侧重于培养学生的实践能力和适应岗位的综合能力。通过这个评价模型，我们能够更好地了解建筑施工测量课程的教学现状以及评价指标的相对重要性。这对于实现高质量的教学和优秀人才的培养具有指导意义。因此，在今后的教学工作中，应特别注重培养学生的实践能力和适应岗位的综合能力。

参考文献：

[1]SaatyTL.Whatistheanalytichierarchyprocess[M].SpringerBerlinHeidelberg，1988.

[2]王慧，曲继鹏，付龙海.基于层次分析法的高校“双师型”教师专业能力评价体系的建立[J].西昌学院学报（自然科学版），2022，36（3）：93-97.

[3]赵琪.基于AHP层次分析法的大学生综合素质评价体系构建[J].上海理工大学学报（社会科学版），2023，45（1）：107-112.

[4]刘健，王小菲.基于层次分析法的高校图书馆网站用户满意度评价指标体系构建研究[J].情报科学，2022，40（12）：80-87.

[5]陶丹.基于AHP分析法的创新教育质量评价标准建构[J].创新创业理论研究与实践，2022，5（19）：10-16.

[6]张晗.基于层次分析法的高校创新创业教育考核体系[J].辽东学院学报（社会科学版），2022，24（4）：127-133.

[7]赵黎明，史慧.高校人才培养模式的实证研究[J].天津大学学报（社会科学版），2015，17（3）：204-209.

[8]薛强，赵静.不同层级生产力促进中心综合评价研究——基于层次分析法[J].广西财经学院学报，2014，27（3）：8-13.

基金项目：柳州铁道职业技术学院校级思政课题“建筑施工测量课程思政示范课”（2023-KCSZ05）；柳州铁道职业技术学院校级教改课题“智慧课堂在铁路工程测量课程中的实践与研究”（2022-JGC07）

作者简介：左海平（1990—），男，汉族，江西吉安人，硕士研究生，讲师，研究方向：职业教育教学改革。