基于单梁试验下的预制T梁起拱度分析及控制研究

汪志甜，孙大定，周小伍，史俊，孙厚超

摘要：为解决预制T梁在生产过程中起拱度精度控制不足的问题，使用百分表对T梁张拉期的起拱度进行全周期监测，并通过理论计算得到预制T梁构件在张拉期增长的起拱度理论值，将监测数据与理论进行相互验证，然后根据预制T梁构件在张拉期、灌浆期和存梁期过程中起拱度的变化情况，分析影响预制T梁起拱度发生变化的主要因素。结果表明，1）张拉期T梁起拱度的监测数据与理论计算结果相吻合；2）张拉期张拉控制应力的设置过高以及在存梁期未采用有效的隔温措施会较大地影响预制T梁起拱度的精确控制。研究结果为预制T梁起拱度精确控制提供了重要参考。

关键词：预制T梁；预应力张拉；起拱度；全周期监测；理论计算

中图分类号：U445.47文献标识码：A文章编号：1006-8023（2024）03-0212-09

Analysis and Control Study of Prefabricated T-beam Arching Based on Single Girder Test

WANG Zhitian1，2， SUN Dading3， ZHOU Xiaowu1，2， SHI Jun4， SUN Houchao5*

（1.Anhui Transport Consulting & Design Institute Co.，Ltd ， Hefei 230088， China; 2.R&D Center for Highway Traffic Energy Saving and Environmental Protection Technology for Transportation Industry， Hefei 230088， China; 3.Anhui Transportation Holding Group CP.， Ltd， Hefei 230000， China; 4.School of Civil Engineering， Central School University， Changsha 410083， China; 5.School of Civil Engineering， Yancheng Institute of Technology， Yancheng 224051， China）

Abstract：In order to solve the problem of insufficient precision control of the arching degree of prefabricated T-beam in the production process， this paper uses the percentage meter to monitor the arching degree of T-beam in the tensioning period of the full cycle， and through theoretical calculations to get the theoretical value of arching degree of prefabricated T-beam members in the growth of the tensioning period， and the monitoring data and theory are verified with each other. Then， according to variations in arching degree of prefabricated T-beam members in the process of the tensioning period， the grouting period， and the storage period， the main factors affecting the change of the arching degree of prefabricated T-beam members are analyzed. The results show that： 1） the full-cycle monitoring data during the tensioning period coincide with the theoretical calculation results; 2） the setting of tension control stress is too high during the tensioning period and the failure to adopt effective insulation measures during the storage period will greatly affect the precise control of the arching degree of precast T-beam. The results of the study provide an important reference for the precise control of the arching degree of precast T-beams.

Keywords：Prefabricated T-beam; prestressing tensioning; arched; full-cycle monitoring; theoretical calculation

0引言

截至2021年底，我国已经设计并建设完成的公路桥梁共有96.11万座，其中中小型桥梁的数量达到81.92万座[1-2]。这些中小型桥梁在建设中大量采用预制预应力混凝土（PC）梁，包括空心板、小型箱梁等不同截面形式，其中T梁截面形式的预制梁不仅在受力方面有着独特的优势，在构造上也具有一定的优越性，在桥梁建设中颇受青睐[3-5]。但在实际施工中，T梁的预制、存放和安装仍存在诸多问题，尤其是起拱度的控制还不够精确。一方面施工人员在预制过程中未采取有效的控制措施，另一方面T梁在预制完成一段时间后才进行安装架设，在存放过程中混凝土会产生收缩和徐变，这些都造成了起拱度的偏差，不利于成桥后对桥面铺装厚度的控制[6-9]。

为了解决T梁在预制过程中起拱度控制方法不足的问题，许多学者对预制T梁起拱度的分析和控制开展了大量研究。向秋燕等[10]分析了预应力T梁在存放期间的影响起拱度发生变化的主要因素，包括混凝土配合比、混凝土集料质量等，并编制了存放期T梁的预拱度值电算程序。陈夏雨等 [11]则认为影响预应力T梁在施工过程中产生起拱度变化的主要因素为预拱度的设置值、预应力束的安装位置、预应力的线型、张拉以及压浆时张拉应力的设置值等，并提出了起拱度不足的解决方法。董建兴[12]则提出了预设下挠度、改进梁体设计和合理安排施工工期等措施来进行起拱度的控制。Hui等[13]对工程中常用的 CEB-FIP-90模型进行了修改，并提出了预制梁新的收缩应变和徐变系数值。Pan等[14]通过试验得出T梁在存梁期，若采用蒸汽养护的温差过大会导致混凝土早期开裂。Zhang等[15]提出了一种新方法，利用弯梁试验同时测定水泥稳定碎石路面的压缩和拉伸动态弹性模量。郭春风[16] 在原有基础上，采用寻求等代梁底均布荷载的思路，并假定预应力作用下产生的箱底最大压应力与等代均布荷载产生的最大压应力相等，提出了预应力混凝土箱梁起拱度的简化算法。杨建国[17]结合施工中所遇到的问题和后张法起拱度计算理论，说明了起拱度随时间的变化趋势。周冰等[18]同样利用后张法的张拉瞬间的起拱度计算理论，结合工程案例，分析起拱度的变化趋势和原因。

综上所述，相关学者对预制T梁起拱度的影响因素进行了许多研究，提出了一系列的解决方法，但对预制T梁整个生产过程监测还不够全面。本研究依托某项目工程实例，研究分析该项目的智能张拉预制T梁生产流程，开展了预制T梁单梁在张拉全过程的预拱度监测试验，与理论计算结果进行对比，验证监控试验的准确性，同时对T梁从张拉、灌浆和存放等阶段进行跟踪测量，分析起拱度的影响因素，拟提出在不同工况下的起拱度控制优化建议。

1工程概况

德州至上饶高速公路的合肥至枞阳段落，北端连通淮南至合肥段，南端与池州长江公路大桥相接。此高速公路项目全程长134.158 km，按照全立交、全封闭的高速公路标准进行建设，设计达到120 km/h，设有双向四车道。桥梁和涵洞的设计符合公路I级荷载要求。由于项目中包含众多桥梁，因此采用了集中预制的方法来生产包括轻型T梁在内的桥梁构件。因此在工程旁特别建设了一个智能化梁场，通过结合质量控制系统和智能场区技术，共同管理预制T型梁的质量。这种工厂化的生产模式相比传统梁场大幅提升了施工效率，在合枞高速上56座桥梁的应用中，近15 km的桥梁建设成本减少了大约5 300万元。

此外，智慧梁场还配备了先进的智能张拉设备，有效避免了人工干预和测量误差，极大提高了张拉作业的效率。尽管如此，张拉完成后预应力束的实际损耗率尚未被检测。为了进一步提高构件的品质，对智能张拉的过程和工艺进行深化研究和优化显得尤为重要。

2理论计算

在测量试验结果之前，先进行起拱度的理论计算，后张预应力预制T梁起拱度由2部分组成：一是由T梁自重所产生的起拱度；二是T梁在张拉预应力筋时所产生的梁体变形。张拉预应力钢筋产生的挠度（f）按式（1）—式（4）计算。

f=-N·e1·L28EI+5N·e2·L248EI。（中性轴在预应力束中间时）（1）

N·e1·L28EI+5N·e2·L248EI。（中性轴在预应力束之上时）（2）

N·e1·L28EI。（预应力束近似直线时）（3）

式中：N为预应力束控制下的张拉力；L为T梁梁长；e1为预应力束中心线与截面中性轴之间的水平距离； e2为预应力束中心线与截面中性轴之间的垂直距离；E 是弹性模量，I是截面惯性矩。

梁体自身重量产生的挠度按式（4）进行计算

f=5ML248×0.85EI 。（4）

式中，M为T梁跨中截面弯矩值。

2.1截面性质计算

试验梁的截面尺寸如图1所示。为方便计算，将截面简化，图1（a）为简等效前梁截面尺寸图，图1（b）为等效后的梁截面尺寸图，简化前后的面积一样，按右图计算其截面性质。

2.2中性轴位置计算

计算公式

y1=12·cH2+d2（B-c）+d′（B′-c）（2H-d′）Bd+hc+B′d′ 。（5）

y2=H-y1 。（6）

式中：y1为梁顶至中性轴的距离；y2为梁底至中性轴的距离；B为T梁截面翼板长度；c为T梁截面腹板长度；d为上T梁截面翼板高度；H为T梁截面高度；h为T梁截面腹板高度；B′为T梁截面马蹄长度；d′为T梁截面马蹄高度。

将梁体参数B=200 cm，c=22 cm，d=24.4 cm，H=160.5 cm，h=107.6 cm，B′=100 cm，d′=28.5 cm代入公式可得：y1=65.50 cm，y2=95.00 cm。

2.3截面惯性矩计算

T梁截面的惯性矩（I）通过式（7）进行计算

I=13（By31+B′y32-（B-c）（y1-d）3-

（B′-c）（y2-d′）3）。（7）

将几何参数代入上式可计算得截面惯性矩：I=3.55×107cm4。

2.4张拉预应力钢筋时的起拱度计算

1）张拉力的确定

本次预制T梁总共有6束预应力钢筋，由生产厂家所给出的数据可以得知，该预应力钢筋的抗拉强度标准值均fpk=1 860 MPa，采用两段张拉的方式进行张拉工艺，设置张拉控制应力值保持在1 395 MPa，则可以得到每束预应力钢筋的锚下控制张拉应力值为232.5 kN。

2）计算参数的确定

由图2可知，跨径为25 m的预制T梁，梁高为1.605 m，张拉的预应力筋为直径15.2 mm低松弛高强度预应力钢绞线，T梁截面上共布置6束钢束，其中，N1钢束包括8根预应力钢绞线，N2和N4钢束包括4根，而N3钢束的预应力钢绞线的数量为6根。

根据图2钢束布置图及其相应断面图，结合中性轴位置可得

e1L2=49.00 cme1k2=69.00 cm

e2L2=11.00 cme2k2=82.00 cm

e3L2=e3k2=80.00 cm

e3′L2=e3′k2=80.00 cm

e4L2=e4k2=82.00 cm

e4′L2=e4′k2=82.00 cm

式中：eiL2为梁端预应力束至中性轴的垂直距离（i=1，2，3，3′，4，4′，分别代表预应力束N1—N4′）；eik2为跨中预应力束至中性轴的垂直距离。构件在张拉预应力钢束时的挠度值计算总结见表1。

综上计算结果可得由预应力束产生的总挠度

f=f1+f2+f3+f3′+f4+f4′=0.848+2.860+5.986+5.986+4.090+4.090=23.86 mm

2.5梁体自重产生的挠度计算

梁体计算截面积（A）为1.01 m2，混凝土容重（Y）为2.6×104 N/m2，由式（4）计算出挠度

f=12.82 mm

2.6理论总挠度计算

综合预应力束产生的总挠度与梁体自重产生的挠度可得应设的预拱度

f1+f2+f3+f3′+f4+f4′-f=23.86-12.82=11.04 mm

3单梁试验

3.1试验方法

该试验的线性测量采用梁底布设百分表的方法进行，测量不同工况下距离梁端不同位置处的起拱度。

3.2试验工况

此试验可分为3个工况。第1个工况为分级张拉预应力钢筋，测量试验梁在张拉不同预应力钢筋后的起拱度，此试验梁分级张拉顺序为：N1→N2→N3（外）→N3（近）→N4（近）→N4（外），为叙述方便，后文将N3（近）简写为N3，N3（外）简写为N3′，N4（近）简写为N4，N4（外）简写为N4′。预应力筋的分孔布置可如图3所示。第2个工况为孔道灌浆，测量试验梁在灌浆后一天之内的起拱度。第3个工况为静置状态，测量试验梁在堆放区静置时的起拱度。

3.3试验测点布置

为测得25 m试验梁在不同工况下的起拱度，在距离跨中0.45、1.35、2.55、4.35、6.45、8.55、10.35、11.7 m处的梁底各布置2个百分表测点，由于对称性，另一侧可不设置测点。共计16个百分表测点，均须在张拉预应力钢筋之前布置完成，测点布置如图4所示。

4试验结果及分析

此次试验对25 m预应力简支T梁进行了6组重复观测，取得了大量不同工况下起拱度的原始数据。现将数据汇集于表格，并绘出相应的起拱度变化曲线。

4.1张拉起拱度

试验从未张拉任何预应力钢筋时记录梁底各个位置百分表的初始数据，每次张拉完一束钢筋，记录一次百分表的数据，以未张拉时作为阶段0，张拉完N4′作为阶段6，整理数据后可得到每次张拉钢束后起拱度的累计值，下面依次列出每组试验的结果。

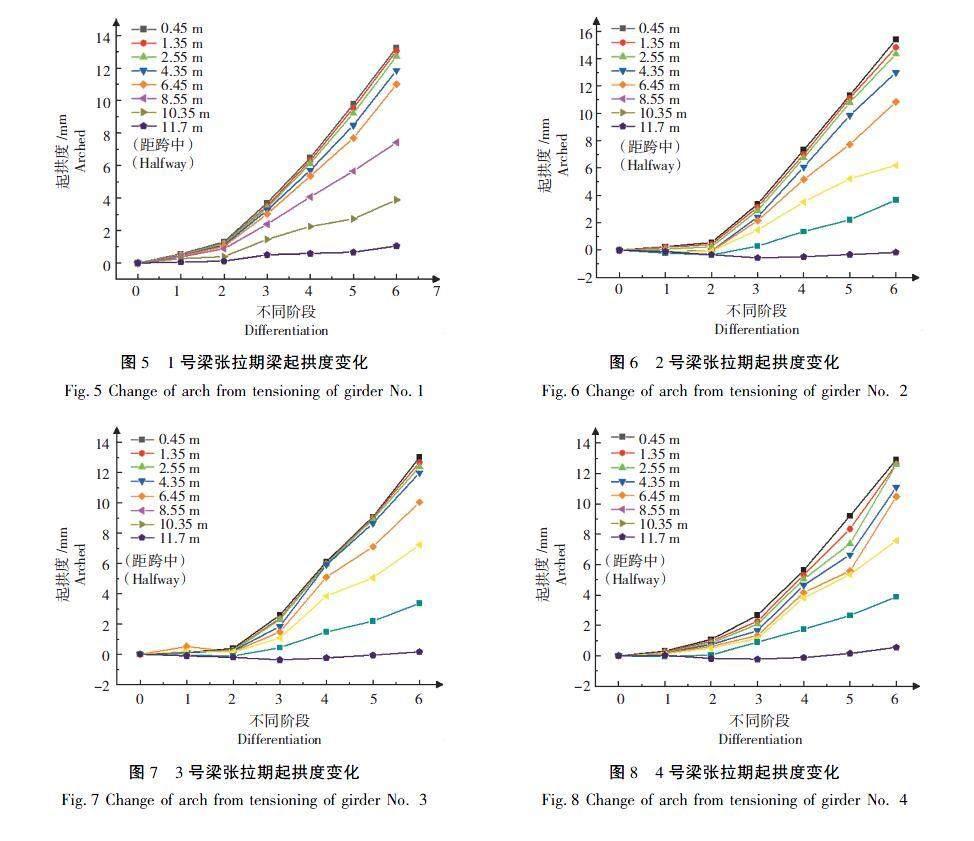
由图5—图10可见，T梁的起拱值随着预应力钢筋的主根张拉而不断增大，且起拱度的增长趋势较为一致。当张拉预应力钢束N1和N2时，试验梁起拱度的增加较小，张拉预应力钢束N3和N4时，试验梁起拱度的增加明显。由此可以得出结论，预应力钢束N3和N4的张拉对试验梁的起拱度起主要控制作用，应做好施工监控。此外，T梁起拱度随跨中向两边逐渐减小，跨中的起拱度在张拉全过程均变化明显，这也与理论情况相符。

4.2灌浆起拱度

灌浆对T梁的起拱度也有一定的影响，观测试验梁在灌浆一天后的起拱值变化，6组距离跨中不同的试验梁，其灌浆起拱度汇总见表2。

由表2可见，灌浆凝结会造成起拱度的增大，但跨中起拱度的变化大小多在1～2 mm，变化并不算很大，故灌浆对起拱度的影响不大。

4.3存梁起拱度

梁在存梁区时，其起拱度会随着时间的增加而逐渐增大，继续采用梁底布设百分表的方法对起拱度进行为期一周的观测，观测间隔为每天1次。6组试验梁的累计起拱度见表3。此表的数据为距离跨中0.45 m处起拱度的数据。

将以上数据绘制成如图11所示，以便观察其起拱度变化趋势。

从以上的观测数据可以看出，试验梁起拱度总的趋势为增大，有少量数据因为环境温度等影响，出现了部分数据下降而产生数据波动的现象，但是总体而言，起拱度随着计算龄期有总体向上增加的趋势。

4.4原因分析及控制措施

从试验梁张拉的实测值与理论值的对比来看，实测值略大于理论值，实测平均起拱度为13.74 mm，理论值为11.04 mm，误差为2.7 mm。分析其原因，首先环境温度是影响试验数据发生波动的直接原因，由于试验梁在进行监测试验时置于无遮蔽的高温场地下，高温导致T梁混凝土水化反应加快，造成T梁上挠，起拱度值增大；其次张拉预应力筋时，施工人员未对张拉控制应力进行精确控制，在张拉工艺时未完全保证每次张拉控制应力完全相同，这也是导致最终的起拱度试验值发生波动的原因。

通过本次试验，可以得出起拱度的控制措施，首先，在张拉预应力筋时，对起拱度值的影响程度较大的预应力束应进行精确控制，例如本次试验的N3、N3′、N4和N4′，张拉控制应力不能过大。其次，高温天气对预应力的影响不可忽视，在施工时，应避免极端高温天气张拉预应力筋，在存梁时也应该适当控制环境温度防止温度过高对T梁起拱值产生影响。最后，对于预应力T梁构件，适当预设下挠度是控制过度起拱的最有效的设计方案，可以根据起拱度的计算结果在梁体底模预设下挠度，从而减小T梁在张拉期和存梁期所可能出现的起拱度上挠的情况。

5结论

1）张拉期，预制T梁的起拱度与预应力张拉的根数呈现一个正相关的趋势，且后几根钢筋的张拉对T梁的起拱度值的影响更大。建议随着张拉过程的进行，对T梁线性控制要求应该更高，与此同时，在张拉全过程，张拉控制应力不宜设置过高，以防止在多次张拉的过程中起拱度无法得到精确控制。

2）灌浆期对预制T梁起拱度的影响较小。

3）存梁期，温度效应、弹性压缩变形和徐变收缩变形相加致使起拱值不断变大，对起拱度的影响也较大。建议在存梁期间采取温度控制措施，减小因环境温度而产生的起拱度波动。

4）本研究提出的计算T梁张拉起拱度的理论算法，为施工单位采用起拱度控制对策的确定提供了依据。计算结果与试验监测结果相差较小，可以认为本次试验所提出来的手算方法可以适用于预制T梁的起拱度预测计算，且方便快捷。

【参考文献】

[1]高中.预应力板梁起拱度偏差大的原因分析及改进措施[J].混凝土世界，2021（6）：92-95.

GAO Z. Cause analysis and improvement measures of large camber deviation of prestressed slab beams[J]. China Concrete， 2021（6）： 92-95.

[2]严忠华.24 m钢梁制作工艺[J].江西冶金，2005，25（5）：15-17.

YAN Z H. Making technology of 24 m steel ridge[J]. Jiangxi Metallurgy， 2005， 25（5）： 15-17.

[3]赵军.简支梁预应力施工中理论起拱度的计算及影响因素分析[J].居舍，2019（26）：20-21.

ZHAO J. Calculation of theoretical camber and analysis of influencing factors in prestressed construction of simply supported beam[J]. Residence， 2019（26）： 20-21.

[4]崔永太.预应力箱梁起拱度控制[J].化工管理，2014（3）：70.

CUI Y T. Control of camber of prestressed box girder[J]. Chemical Enterprise Management， 2014（3）： 70.

[5]王开凤.预应力混凝土简支梁起拱度计算方法的研究[J].交通科技，2001（5）：10-11.

WANG K F. A study of arching calculation of prestressed concrete simple beams[J]. Transportation Science & Technology， 2001（5）： 10-11.

[6]任雅露，张瀚浩.基于单梁试验下的预制PC小箱梁起拱度分析[J].市政技术，2018，36（1）：60-63.

REN Y L， ZHANG H H. Analysis of the inverted camber of precast PC small box girder based on single beam test[J]. Municipal Engineering Technology， 2018， 36（1）： 60-63.

[7]耿波.预应力混凝土梁的起拱度控制方法及试验研究[D].武汉：武汉理工大学，2004.

GENG B. Control methods and experiment research in deflection upwards of P.C. beams[D]. Wuhan： Wuhan University of Technology， 2004.

[8]赵军.简支梁预应力施工中理论起拱度的计算及影响因素分析[J].居舍，2019（26）：20-21.

ZHAO J. Calculation of theoretical camber and analysis of influencing factors in prestressed construction of simply supported beam[J]. Residence， 2019（26）： 20-21.

[9]时炜.基于智能建造的装配式T梁智能张拉流程优化研究[J].交通科技与管理，2023，4（13）：5-8.

SHI W. Research on intelligent tensioning process optimization of assembled T-beam based on intelligent construction[J]. Transportation Technology and Management， 2023， 4（13）： 5-8.

[10]向秋燕，喻泽红.桥梁上拱度的理论算法[J].中国水运（下半月），2009，9（1）：211-212，217.

XIANG Q Y， YU Z H. Theoretical algorithm of camber on bridge[J]. China Water Transport， 2009， 9（1）： 211-212， 217.

[11]陈夏雨，陈冲彦.预制T梁起拱高度不够的分析与解决[J].江西建材，2015（4）：122-123.

CHEN X Y， CHEN C Y. Analysis and solution of insufficient arching height of precast T-beam[J]. Jiangxi Building Materials， 2015（4）： 122-123.

[12]董建兴.装配式预应力混凝土T梁起拱度控制[J].山西交通科技，2005（S1）：105-106，111.

DONG J X. The control of assembling prestress concrete T beam springing degree[J]. Shanxi Science & Technology of Communications， 2005（S1）： 105-106， 111.

[13]HUI Q X， YAN L， ZHANG Z Q， et al. Shrinkage and creep effect analysis of beam-arch composite bridge based on field test[J]. Structures， 2024， 62： 106187.

[14]ZOU P， CHANG H J， WANG F， et al. Effect of steam curing scheme on the early-age temperature field of a prefabricated concrete T-beam[J]. Case Studies in Construction Materials， 2024， 20： e02787.

[15]ZHANG J， WANG S X， CUI J， et al. Simultaneous determination of cement stabilized macadam's dynamic resilient modulus in compression and tension by bending beam test[J]. Case Studies in Construction Materials， 2024， 20： e03008.

[16]郭丰春.预应力混凝土箱梁起拱度的快速算法及应用[J].湖南交通科技，2010，36（2）：102-103，116.

GUO F C. Quick algorithm for arching degree of prestressed concrete box girder[J]. Hunan Communication Science and Technology， 2010， 36（2）： 102-103， 116.

[17]杨建国.后张法预应力简支梁起拱度的计算及应用[J].山西建筑，2007，33（18）：325-326.

YANG J G. Spring quantum calculation of prestressed simple supported beam with post-tensioned method and its application[J]. Shanxi Architecture， 2007， 33（18）： 325-326.

[18]周冰，张艳芳，王毅明.后张法预应力简支梁起拱度计算及施工应用[J].铁道建筑，2007，47（3）：11-12.

ZHOU B， ZHANG Y F， WANG Y M. Calculation of camber for prestressed simply-supported girder with post-pretensioning method and its use in construction[J]. Railway Engineering， 2007， 47（3）： 11-12.