林业剩余物可调式斜进料盘式削片机主轴刚柔耦合动力学分析

田菲，宋鹏，任长清，丁禹程

摘要：研究新型枝丫材、抚育间伐材等林业剩余物盘式削片机的主轴系统，该削片机刀盘与主轴安装结构的特点，与当下主流安装形式存在差异，验证其主轴系统在切削原木过程中是否符合结构设计要求。采用ADAMS软件与ANSYS软件建立柔性主轴的刚柔耦合模型，在模型中添加切削力周期变化的规律，仿真提取主轴与刀盘连接点位置处主轴轴向与径向振幅情况，得到刀盘在径向的最大振动幅度为175 μm，结果按国标对比符合旋转轴长期运行条件。研究结果对新型削片机主轴系统的合理性提供了验证，为削片机主轴系统的结构改进提供了理论依据。

关键词：林业剩余物；盘式削片机；主轴系统；刚柔耦合；动力学仿真

中图分类号：S777文献标识码：A文章编号：1006-8023（2024）03-0152-10

Dynamic Analysis of Rigid-flexible Coupling of Spindle of Adjustable Oblique Feed Disc Chipper for Forestry Residues

TIAN Fei1， SONG Peng2， REN Changqing2*， DING Yucheng2

（1.Heilongjiang Provincial Forestry and Grassland Survey Planning and Design Institute， Suihua 152001， China; 2.College of Mechanical and Electrical Engineering， Northeast Forestry University， Harbin 150040， China）

Abstract：In this paper， the spindle system of the new disc chipper for forestry residues such as branch wood， tending timber and thinning timber was studied， and the installation structure of the cutter head and spindle of the chipper was different from the current mainstream installation form， and it was necessary to verify whether the spindle system met the structural design requirements in the process of cutting logs. ADAMS software and ANSYS software were used to establish the rigid-flexible coupling model of the flexible spindle， the law of the periodic variation of cutting force was added to the model， and the axial and radial amplitudes of the spindle at the connection point between the spindle and the cutter head were simulated and extracted， and the maximum vibration amplitude of the cutter head in the radial direction was 175μm， which met the long-term operation standard of the rotating shaft stipulated in the Chinese national standard. This study provides a verification of the rationality of the new chipper spindle system， and provides a theoretical basis for the structural improvement of the chipper spindle system.

Keywords：Forestry residue; disc chipper; spindle system; rigid-flex coupling; dynamics simulation

0引言

我国的林业剩余物约占全球储量的2.4%，储量居于世界第9位，其中枝丫材、抚育间伐材的存量巨大，可以作为人造板产业的生产原料[1]。枝丫材、间伐材不仅成本低廉，而且径级较小，其纤维结构致密，生产出的纤维板在强度、耐用性方面更具优势，属于纤维板生产的理想原料。

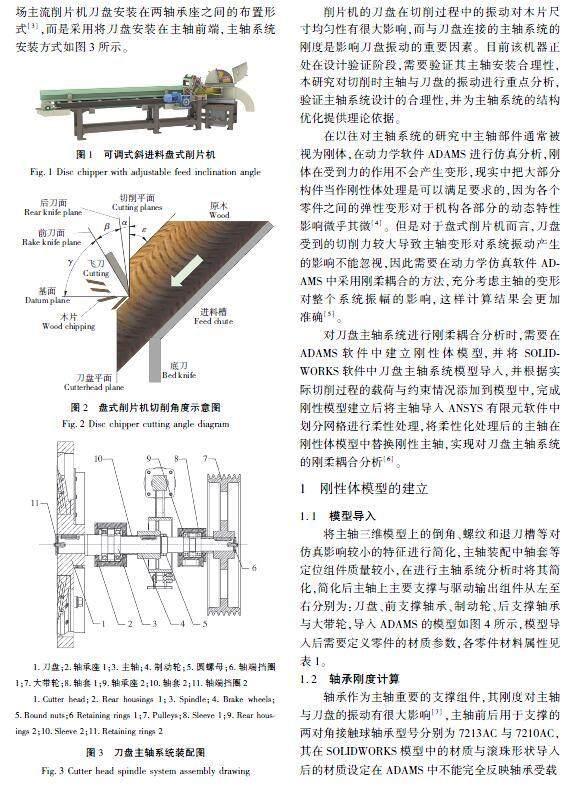
纤维板的质量与剩余物加工后工艺木片的形状与尺寸均匀性密切相关，当下国内外大部分枝丫材盘式削片机均为刀盘固定安装在机架底座上[2]，无法根据生产情况对木片尺寸形状进行实时调整。如图1所示。本研究对象为一款自主设计的新型林业剩余物可调式斜进料盘式削片机。盘式削片机切削过程的刀具角度如图2所示，图2中ε、α、β、γ分别为切削过程中的进料倾斜角、飞刀后角、飞刀楔角、飞刀前角，该型削片机正是通过调整进料倾斜角（ε）实现对木片尺寸的调节。该机器为方便实现切削装置的角度调整，其主轴系统不同于当下市场主流削片机刀盘安装在两轴承座之间的布置形式[3]，而是采用将刀盘安装在主轴前端，主轴系统安装方式如图3所示。

削片机的刀盘在切削过程中的振动对木片尺寸均匀性有很大影响，而与刀盘连接的主轴系统的刚度是影响刀盘振动的重要因素。目前该机器正处在设计验证阶段，需要验证其主轴安装合理性，本研究对切削时主轴与刀盘的振动进行重点分析，验证主轴系统设计的合理性，并为主轴系统的结构优化提供理论依据。

在以往对主轴系统的研究中主轴部件通常被视为刚体，在动力学软件ADAMS进行仿真分析，刚体在受到力的作用不会产生变形，现实中把大部分构件当作刚性体处理是可以满足要求的，因为各个零件之间的弹性变形对于机构各部分的动态特性影响微乎其微[4]。但是对于盘式削片机而言，刀盘受到的切削力较大导致主轴变形对系统振动产生的影响不能忽视，因此需要在动力学仿真软件ADAMS中采用刚柔耦合的方法，充分考虑主轴的变形对整个系统振幅的影响，这样计算结果会更加准确[5]。

对刀盘主轴系统进行刚柔耦合分析时，需要在ADAMS软件中建立刚性体模型，并将SOLIDWORKS软件中刀盘主轴系统模型导入，并根据实际切削过程的载荷与约束情况添加到模型中，完成刚性模型建立后将主轴导入ANSYS有限元软件中划分网格进行柔性处理，将柔性化处理后的主轴在刚性体模型中替换刚性主轴，实现对刀盘主轴系统的刚柔耦合分析[6]。

1刚性体模型的建立

1.1模型导入

将主轴三维模型上的倒角、螺纹和退刀槽等对仿真影响较小的特征进行简化，主轴装配中轴套等定位组件质量较小，在进行主轴系统分析时将其简化，简化后主轴上主要支撑与驱动输出组件从左至右分别为：刀盘、前支撑轴承、制动轮、后支撑轴承与大带轮，导入ADAMS的模型如图4所示，模型导入后需要定义零件的材质参数，各零件材料属性见表1。

1.2轴承刚度计算

轴承作为主轴重要的支撑组件，其刚度对主轴与刀盘的振动有很大影响[7]，主轴前后用于支撑的两对角接触球轴承型号分别为7213AC与7210AC，其在SOLIDWORKS模型中的材质与滚珠形状导入后的材质设定在ADAMS中不能完全反映轴承受载能力，对此采用ADAMS中专用模块Machinery重新创建轴承属性，将轴承设置为柔性。ADAMS中默认刚度参数为轴承平均参数与实际轴承组的刚度有偏差，通过设置轴承参数以达到角接触球轴承面对面安装的等效性能，通过式（1）来计算轴承组的轴向刚度[8]。

Ja=32K（m23+n23）·F13a。（1）

式中：Ja为组配轴承组轴向刚度，N/mm；m为组配轴承组中7213AC轴承的个数；n为组配轴承组中7210AC轴承的个数；Fa为轴向载荷，N；K为弹性变形综合系数，对于K，可用式（2）计算。

K=0.004 36φ13·z23·sin53λ。（2）

式中： φ为滚子直径，mm；z为滚子数量；λ为轴承的接触角，（°）。轴承参数见表2。

通过表2中提供的参数计算出前后两对轴承的弹性变形综合系数分别为：K1=1.07×10-3，K2=1.23×10-3。将两组K代入式（1）中，m、n均为2，主轴系统的轴向载荷Fa主要是刀盘上的飞刀前刀面对原木的切削力水平方向的单位切削分力Frx，其计算式如式（3）所示[9-10]。

FrX=l·b·τ·cos（α+β+φγ）cos（α+β+ε+φγ-90°）-fc·sin（α+β+ε+φγ-90°）。（3）

式中：α、β、ε分别为飞刀后角、楔角、进料倾斜角；φγ为前刀面与木材摩擦角；l木片纤维长度，m；b为刀刃与原木接触宽度，m；原木顺纤维抗剪强度，Pa；fc为法向压力时木材顺纹剪切附加阻力系数，取值0.3。为计算单位切削分力，将b设为1 m，将木片纤维长度0.02 m，速生杨木顺纹抗剪强度τ=5.7×106 Pa，飞刀后角4°，飞刀楔角38°与前刀面摩擦角16.7°。根据进料倾斜角可调式盘式削片机的设计参数，进料倾斜角ε可以在30°～45°调整。为了验证切削力最大情况下刀盘与主轴振动的情况，取切削力最大时的进料倾斜角，为反映Frx对ε的变化情况，将式（3）用MATLAB软件，将各常数带入公式后以ε为变量得到水平方向上单位切削分力的图像，如图5所示，根据图像得到Frx在ε=45°时取得最大值65 769.4 N/m。

水平方向上单位切削力Frx与主轴系统的轴向载荷Fa之间的关系见式（4）。当切削最大直径为0.16 m的原木时，轴承上的轴向载荷Fa为1 052.3 N，代入式（1）中，求出前轴承组轴向刚度Ja1=45 258.3 N/mm、后轴承组轴向刚度Ja2=39 375.3 N/mm。

Fa=Frx×b。 （4）

轴承组的径向刚度（Jr）根据式（5）计算。

Jr=Jr1+Jr2

Jr1=（2κ-1）·m2/3·Jr（κ）·F1/3aK1·Ja（κ）·tan2λ

Jr2=（2κ-1）·n2/3·Jr（κ）·F1/3aK2·Ja（κ）·tan2λ。（5）

式中：κ为载荷分布系数；Jr为径向载荷分布系数；Ja为轴向载荷分布系数。在径向载荷Fr、轴向载荷Fa和实际接触角已知的条件下，可根据Fr·tanλ/Fa的计算值，查表3得到κ、Jr （κ）和Ja （κ），若数值介于表中计算值之间时，允许通过线性插值法进行计算[11]。

主轴上的径向载荷Fr在削片机生产过程中随切削力不断变化，在轴承径向刚度计算时取最大值，主要为前刀面对原木的径向切削分力，以直径160 mm的杨木为例，Frx约为1 729 N。求出Fr·tanλ/Fa为0.766 2，在表3中介于0.783 5～0.742 7，采用拉格朗日插值法计算其对应的κ、Jr （κ）、Ja（κ），设Fr·tanλ/Fa为x。

ε=0.742 7-x-0.040 8·0.6+x-0.783 5-0.040 8·0.7。（6）

Jr（ε）=0.742 7-x-0.040 8·0.241 6+x-0.783 5-0.040 8·0.250 5。（7）

Ja（ε）=0.742 7-x-0.040 8·0.380 4+x-0.783 5-0.040 8·0.337 4。（8）

将x=0.766 2代入上述公式，分别计算出κ=0.642 4、 Jr（κ）=0.245 4、Ja（κ）=0.362 2，再将计算出的值代入式（5），m、n均为2，κ=25°，K1=1.07×10-3，K2=1.23×10-3，求出前轴承组径向刚度Jr1=13 390.9 N/mm与后轴承组径向刚度Jr2=11 649.0 N/mm。将得到的前后轴承径向与轴向刚度输入到ADAMS中，并设置预载荷。

1.3切削情况分析

切削力的添加在飞刀刀刃位置，由于飞刀在切削时切削力随刀刃与木材接触面积不断变化，且切削力F与接触长度b成正比，其关系式见式（9）。刀盘在额定转速情况下飞刀刀刃与原木的接触长度（s）与时间（t）是一个有规律的周期性函数，将切削力函数添加入ADAMS中仿真出刚性主轴与刀盘在连续切削下的振动情况。

F=F′×b。（9）

式中：F为切削力，N；F′单位切削力，N/m；b为刀刃与原木接触宽度，m。

由于实际生产过程中原木直径不一致并且其存在枝丫弯曲等情况，无法完全模拟出切削力的真实情况，因此在对切削力变化分析时，为了模拟出主轴与刀盘在切削时可能的最大振幅，以160 mm最大直径的小径木作为对象进行分析。在分析切削力变化过程时需要假设剥完皮后的小径木通体圆直，其横截面为标准圆，且以一把飞刀连续切削为例进行切削力模拟。

为了验证刀盘与主轴的振动情况，原木以一定倾斜角度进料，切削力在进料倾斜角ε为45°时取到最大，因此选取进料倾斜角为45°，由图6（a）可知，当直径d=160 mm时，斜切的实际原木截面为椭圆，其椭圆短半轴a1=80 mm与长半轴b1=113 mm。实际切削时，原木在飞刀的切削分力的作用下会紧紧抵住进料口底刀与侧底刀位置，原木椭圆截面与飞刀的相对位置如图6（b）所示。图6中进料口与刀盘中心相对位置标出，为了方便表示各点的位置，以刀盘回转中心为原点建立坐标系。

图6中A、B 为飞刀与椭圆接触点，2点之间的距离即飞刀刀刃与原木接触宽度。为方便计算飞刀一次切削的周期，C、D 为飞刀恰好切入与切出点，根据切削装置三维模型中的距离，可以得到2点坐标分别为（-176，-198）与（54，-209），椭圆中心点坐标E为（-60，-215）。当刀盘以额定转速630 r/min转动时，飞刀刀刃相对于刀盘回转中心的角速度ω=3 780°/s。根据图中C点与D点坐标可得出∠COD=56.1°，由此可以算出每把飞刀一次切削与原木接触时间周期为0.014 84 s。

设计的飞刀刀刃对刀盘回转中心有10°偏转角，A、B 连线所在的直线相对于坐标原点O的斜率以及与X轴、Y轴的接触点均随刀盘转动而变化。若采用直线方程与椭圆方程联立求解的方法来解析接触宽度随时间变化的方程，经过尝试后发现直线方程表达式变化过于复杂，且当直线AB与Y轴平行位置处方程不连续，不易通过解析法实现。

采用线性回归的方法获取接触宽度关于角度的函数关系，由于在SOLIDWORKS三维图中可以通过测量2点距离得到在各角度下AB连线的长度，可以获得足够多的样本点进行拟合，当样本点足够多时拟合方程表达出的切削规律与真实情况误差较小。

样本点的数据测量是在SOLIDWORKS草图中根据飞刀与进料口的坐标位置，按照飞刀从C点切入到D点切出时的轨迹，获取飞刀与原木椭圆截面相交部分的长度，为了获得尽可能准确的拟合曲线，在圆弧CD轨迹中均匀选取50个样本点。以C点为起始点，每个样本点的刀刃相对于上一个样本点绕刀盘回转中心O转过1.112°，一共转过56.1°到达D点，样本点选取方式如图7所示。

测量过样本点后数据拟合出四阶回归曲线方程为

φ（x）=-0.000 2x4+0.023 4x3-1.055 6x2+

20.446 x+25.695 。（10）

进行线性回归时，R2为回归平方和与总离差平方和的比值，这一比值越大，表示总离差平方和中可以由回归平方和解释的比例越大，模型越精确，回归效果越显著。从数值上说，R2介于0、1之间，越接近1，回归拟合效果越好，一般认为超过0.8的模型拟合优度比较高[12]。该回归模型中的残差平方和R2为0.985 4，接近于1，该拟合曲线回归方程的准确度满足切削力规律需要，样本点回归曲线如图8所示。

将刀刃与原木接触宽度随角度变化函数转化为切削力随时间变化的关系式，上式中变量角度（x）替换为角速度（ω）与时间（t）的乘积，并且角速度（ω）已知为3 780°/s，转化后的关系式为式（11）。一个切削周期飞刀经过的时间t为0.014 84 s，切削力在刀盘上引起刀盘与主轴振动主要是来自前刀面在竖直方向上的分力，模拟振动情况在刀盘上施加径向载荷，在上文中计算的飞刀前刀面在切削45°杨木的单位切削力 为65.769 4 N/mm。

F=65.769 4·（-40 831 674 910t4+1 263

837 557t3-15 082 835t2+77 285.88t+

25.695），t∈（0，0.014 84）。（11）

式中：F为切削力，N；t为一把飞刀切削周期内的时间，s。为了更直观反映切削力周期变化的趋势与极值，将式（11）代入MATLAB中作出切削力在周期内的变化曲线，生成的曲线如图9所示。

根据图9中的切削力图像，可以看出飞刀进入切削的瞬间切削力增加到1 786 N，随着刀盘转动切削力的增速逐渐放缓，最大切削力达到11 022.5 N，随着刀刃逐渐切出原木，切削力逐渐降低。将图9中切削力变化规律添加到ADAMS中，为了在ADAMS中体现出切削力变化周期，将切削力变化趋势分解为多段step函数，采用ADAMS中mod求余函数实现以0.014 84 s的周期循环，周期函数与切削力添加图像如图10所示。

1.4主轴系统刚性体动力学仿真

创建零件在装配体中的运动副与约束，主轴与刀盘之间通过键连接同步转动两者位置与运动情况一致，主轴通过平键与刀盘连接，因此在ADAMS中在键连接位置处添加固定副；同理在主轴与大带轮以及制动轮的键连接处也添加固定副；主轴系统通过带轮驱动，因此带轮作为系统的主动件在其与地面之间添加转动副，在转动副上添加转速630 r/min经过单位转换后的3 780°/s的旋转驱动;添加向下的重力加速度9.8 N/kg；最后将计算出的切削力随时间周期性变化规律，通过设置函数添加到刀盘上飞刀刀刃中心位置，施加过载荷与驱动的模型如图11所示。

对施加过载荷与约束的多刚体模型求解，获取刀盘在切削情况下刚性主轴与振幅情况，为柔性主轴分析提供参照。刀盘振动会影响木片切削效果，因此测量点选择刀盘与主轴连接处，仿真结果如图12与图13所示。由于刚性主轴在轴向上有角接触球轴承限制，因此X方向几乎不存在轴向振动；其轴承支承点受到切削力径向分力导致测量点在Y方向上与Z方向上测量点均有振动，分别朝Y轴负方向和Z轴的正方向偏移，其位移幅度控制在30 μm以内。

参考国家标准《旋转径向振动的测量和评定（GB/T 11348.1—1999）》，最大位移峰值S（p-p）max根据式（12）进行计算。

S（p-p）max=（Sy（p-p））2+（Sz（p-p））2 。（12）

式中：S（p-p）max为最大位移峰峰值；Sy（p-p）为Y向位移峰峰；Sz（p-p）为Z向位移峰峰值，将图13中的位移幅度30 μm代入，得到刚体动力学仿真结果刀盘与主轴连接点位移幅度为42.5 μm。

2建立刚柔耦合模型

把模型当作刚性系统来处理时，仅将轴承柔性化，振动时刚性主轴变形不明显，为了更准确地求出刀盘与主轴连接处的振动情况，需要将主轴进行柔性化处理。利用有限元软件ANSYS将构件划分网格并进行模态计算，利用ANSYS与ADAMS双向数据接口可以处理柔性部件的替换，使ADAMS软件中在相同条件下仿真得到更为真实的切削振动情况。

柔性化步骤[13-16]

（1）将主轴模型导入ANSYS。

（2）设置单元类型与材料属性。

（3）网格划分，划分后的网格如图14所示。

（4）在轴承支撑位置创建刚性节点。

（5）求解模态生成结果文件。

在ANSYS中求解出主轴六阶模态频率，把结果文件保存成mnf格式。ADAMS中导入柔性体文件为mnf格式，该文件格式包含了主轴模态信息[17-18]，是柔性零件替换的中性文件，替换后的刚柔耦合动力学模型如图15所示。

3刚柔耦合仿真结果分析

将刚柔耦合动力学模型进行求解，仍然以刀盘与主轴连接点为测量点，这次得到测量点在X轴方向上由于主轴的柔性变形产生了一定振动，轴向上最大位移幅度达到190 μm，振幅随时间变化逐渐减小，可能的原因是刚开始切削时主轴受到冲击力，轴向上产生了弹性变形，随后周期性的切削力主要是沿径向作用，因此主轴轴向的振动被轴承与弹性变形吸收振幅逐渐减弱。

测量点在Y、Z轴上的振幅，与刚体动力学模型仿真结果相比更大，也反映了主轴的弹性变形增加了刀盘的振动，其Y向最大位移幅度约在150 μm，Z向最大位移幅度约在90 μm，将结果带入式（12）求出S（p-p）max为175 μm。将刚柔耦合动力学仿真结果与刚体动力学仿真结果相比，将主轴柔性化后得出的振幅更大，且轴向也出现小幅振动，刚柔耦合后的振幅结果更接近真实状态。

依据GB/T 11348.3—2011对振幅情况评价，其中将旋转轴的振动情况分为4个评价区域A、B、C、D，当振幅介于A、B两级内认为振动是可接受并能无限制长期运行的；当振动幅度处于C区域时，可以有限运行一段时间，但对于长期运行的机器是不合格的；D区域则可认为无法平稳运行。区域划分边界的推荐值与主轴的转速有关，区域边界计算见式（13）

SAB（P-P）=4 800/n

SBC（P-P）=9 000/n

SCD（P-P）=13 200/n。  （13）

将削片机额定转速630 r/min代入式（13），求解出AB区域界限为191 μm，削片机径向振幅175 μm小于AB区域分界线的191 μm，介于区域A内，因此得出削片机在工作时主轴系统能满足使用条件可以长期运行。

4结论

本研究针对一款尚处于设计中的新型的林间剩余物可调式斜进料盘式削片机的主轴安装形式进行分析，通过计算添加周期性切削力载荷模拟出切削过程中刀盘上飞刀的受力情况，建立相对真实的动力学模型后，得出以下结论。

1）将盘式削片机主轴系统的刚性体与刚柔耦合后的动力学模型仿真结果进行对比，发现主轴为柔性时刀盘与主轴连接处的振动情况更符合实际切削效果。

2）对刚柔耦合仿真结果按照国家标准进行振幅评价，结果显示该机型的主轴系统能满足长期使用条件。

3）经过本研究对主轴系统的刚柔耦合动力学仿真分析，为新型削片机主轴系统的合理性提供了验证，并为以后削片机主轴系统的结构改进提供了参考依据。

【参考文献】

[1]战丽，张志文，杨春梅，等.履带式林间剩余物集材机关键部件设计与试验研究[J].森林工程，2023，39（3）：131-139.

ZHAN L， ZHANG Z W， YANG C M， et al. Design and experimental study on key components of crawler forest residue skidder[J]. Forest Engineering， 2023， 39（3）： 131-139.

[2]LABBE S， AUCHET S， MEAUSOONE P J. Effect of anvil position on cutting force and energy measurements of a disc chipper[J]. Biomass and Bioenergy， 2017， 99： 49-56.

[3]花军，陈光伟.木材加工机械[M].北京：科学出版社，2017.

HUA J， CHEN G W. Woodworking machinery[M]. Beijing： Science Press， 2017.

[4]李荣丽，贺利乐.煤炭采样机械臂的刚柔耦合动力学建模与仿真分析[J].机械设计，2013，30（8）：33-36.

LI R L， HE L L. Dynamic modeling and simulation analysis for rigid-flexible coupling model of coal sample manipulator[J]. Journal of Machine Design， 2013， 30（8）： 33-36.

[5]任长清，王涛，丁星尘，等.木窗双端复合精铣加工机床主轴系统的刚柔耦合动力学建模与仿真[J].森林工程，2023，39（5）：133-143.

REN C Q， WANG T， DING X C， et al. Rigid-flexible coupled dynamics modeling and simulation of spindle system of double-end compound finishing milling machine tool for wooden window[J]. Forest Engineering， 2023， 39（5）： 133-143.

[6]贾磊，朱彦齐.基于SolidWorks与ADAMS的工业机器人动力学仿真[J].包装工程，2020，41（3）：207-210.

JIA L， ZHU Y Q. Dynamic simulation of industrial robot based on SolidWorks and ADAMS[J]. Packaging Engineering， 2020， 41（3）： 207-210.

[7]黄贤振，于瑞，刘慧珍，等.考虑轴承非线性恢复力的主轴振动可靠性分析[J/OL].吉林大学学报（工学版），1-9[2024-01-27].https：//doi.org/10.13229/ j.cnki.Jdxbgxb.20230295.

HUANG X Z， YU R， LIU H Z， et al. Reliability analysis of spindle vibration considering nonlinear recovery force of bearing[J/OL]. Journal of Jilin University （Engineering Science），1-9[2024-01-27]. https：//doi.org/10.13229/ j.cnki.Jdxbgxb.20230295.

[8]陈润霖，赵少东，张梦豪，等.角接触球轴承的时变刚度模型与承载特性分析[J].机械设计与研究，2022，38（2）：114-119.

CHEN R L， ZHAO S D， ZHANG M H， et al. Time-varying stiffness model and load-bearing characteristics analysis of angular contact ball bearings[J]. Machine Design & Research， 2022， 38（2）： 114-119.

[9]刘旭东.移动式林间剩余物粉碎机理论分析与试验研究[D].哈尔滨：东北林业大学，2019.

LIU X D. Theoretical analysis and experimental study on mobile forest residue crusher[D]. Harbin： Northeast Forestry University， 2019.

[10]薄仕文，李耀翔，王海滨.灌木切割试验装置切割振动分析[J].森林工程，2022，38（5）：75-82.

BO S W， LI Y X， WANG H B. Cutting vibration analysis of shrub cutting experimental device[J]. Forest Engineering， 2022， 38（5）： 75-82.

[11]张中元，王丽红，原起富.多联组配角接触球轴承的刚度计算[J].制造技术与机床，2004（2）：102-104.

ZHANG Z Y， WANG L H， YUAN Q F. Rigidity calculation for combined angular contact ball bearings[J]. Manufacturing Technology & Machine Tool， 2004（2）： 102-104.

[12]夏玉国，彭友志，刘正华，等.线性回归拟合的测量不确定度评定[J].计量学报，2023，44（4）：664-670.

XIA Y G， PENG Y Z， LIU Z H， et al. The measurement uncertainty evaluation of linear regression fitting[J]. Acta Metrologica Sinica， 2023， 44（4）： 664-670.

[13]李明昊，牛昊，范佳艺，等.刚柔耦合仿生机器鱼传动轴动态疲劳可靠性分析[J].中国工程机械学报，2023，21（4）：358-362.

LI M H， NIU H， FAN J Y， et al. Rigid-flexible coupling dynamic fatigue reliability study on bionic fish driving shaft[J]. Chinese Journal of Construction Machinery， 2023， 21（4）： 358-362.

[14]LI T T， DU W， PIAO M W， et al. Dynamical effect investigations of component's internal interface by using techniques of rigid-flex coupling simulation[J]. Shock and Vibration， 2021， 2021： 6509950.

[15]杨起帆，葛继鹏，齐英杰，等.基于ANSYS的数控裁板锯主机结构有限元强度分析[J].森林工程，2023，39（6）：126-133.

YANG Q F， GE J P， QI Y J， et al. Finite element strength analysis of the main frame of CNC cutting board saw based on ANSYS[J]. Forest Engineering， 2023， 39（6）： 126-133.

[16]郑思远，田俊杰，王立鹏，等.紧凑型刚柔耦合腰部康复机器人设计与分析[J/OL].机械工程学报，1-11[2024-01-27].https：//kns-cnki-net. Webv pn .nefu.edu.cn /kcms/ detail/11.2187.TH.20231229.1427.036.html.

ZHENG S Y， TIAN J J， WANG L P， et al. Design and analysis of compact rigid-flexible coupled waist rehabilitation robot[J/OL]. Journal of Mechanical Engineering， 1-11[2024-01-27]. https：//kns-cnki-net.webvpn.nefu.edu.cn/kcms/ detail/11.2187. TH.20231229.1427.036.html.

[17]魏大栋.采煤机截割部刚柔耦合动力学及扭矩轴模态分析[J].机械管理开发，2022，37（7）：75-76，79.

WEI D D. Analysis of rigid-flexible coupling dynamics and torque axis modalities of coal miner cutoff section[J]. Mechanical Management and Development， 2022， 37（7）： 75-76， 79.