一种只需功率测量的相控阵天线分组校准方法

王福宇 陈文俊 卢青

摘要：相控阵天线收发通道中存在的较大幅相误差会造成辐射方向图畸变，引起天线增益的下降和副瓣的升高。为了获得理想的天线方向图，文章提出了一种基于功率测量的相控阵天线分组校准方法，除了测量一次阵列总的阵列功率外，对阵列元件只需再进行一次相移和两次功率测量就可以确定单元相对幅相分布。为使校准过程中合成辐射场信号变化明显，该方法使用分组矩阵将阵列进行分组，校准时同时改变多个单元相位，将功率测量值代入公式解算得出所有单元的幅相分布。对12×12元阵列的仿真结果表明：使用该方法校准后，天线方向图副瓣电平显著降低，方向图主瓣与理论值基本一致，达到校准效果。

关键词：天线校准；相控阵天线；分组校准；功率测量

中图分类号：TN820  文献标志码：A

0 引言

相控阵天线在现代雷达和无线通信系统中发挥着非常重要的作用。由于一些不可避免的误差和不确定性，如机械制造公差、温度变化以及电子和射频部件老化等，实际的阵列元件复激励偏离了理想值，导致辐射方向图失真并降低整体性能。因此，为保持相控阵天线的良好性能，厂商在相控阵天线出厂之前以及使用期间，需要通过测量阵列元件激励并对幅相误差进行校准和补偿。

目前，常用的天线校准方法有近场扫描法、旋转矢量法（REV法）、互耦校准法、换相测量法等［1-3］。根据校准时测量数据类型不同，校准方法又分为需幅相测量的方法和仅幅度测量的方法［4］。旋转矢量法是典型的仅需幅度测量的方法，将一个单元的相位从0°变化到360°，其他单元相位不变，测量总功率变化，通过数学计算确定阵面相对幅相分布，所需校准设备简单，但测量次数过多。刘明罡等［5］结合傅立叶分析对旋转矢量法进行了改良，使用Hadamard矩阵将阵元进行分组，同时改变多个单元相位使总体信号变化更显著，提高校准速度和精度。齐宏业等［6］通过测量3种不同配相下的总功率值，计算得出各个单元的幅相值，减少了功率测量次数，提高了校准时效性。王迪等［7］提出了一种新的联合校准方法，对阵元分组后使用REV法，同时使用最小二乘法拟合功率曲线，求得每个阵元的幅值和相位。

本文提出了一种基于功率测量的相控阵天线分组校准方法，除了测量一次阵列初始相位下总功率外，每次改变相位对阵列只需进行2次功率测量就可以确定单元的相对幅相分布，且为使在校准过程中合成辐射场信号变化明显，使用分组矩阵将天线阵列进行分组，校准时同时改变多个单元相位，代入公式解算得出所有单元的幅相分布。对12×12元阵列的仿真结果表明：使用该方法校准后能够达到校准效果。

1 测试原理

对于N元相控阵天线，为了进行校准，需要求解每个阵元的幅度和相位值，即总共有N个未知量。为了求解这N个未知量，需要建立N个方程。但如果每次测量前只改变一个单元的相位，阵面总功率变化非常微弱，且容易受到非线性信号和接收机噪声的干扰。因此，本文将天线阵面划分为N种组合，每种组合内均包含部分相位改变单元以及相位不变单元，校准时同时改变所有相位改变单元的相位后，再对阵面总功率进行测量。

设En和n表示第n个天线元件的振幅和相位，n=1，2，…N。相控阵天线的总电场E可以描述如下：

E=∑Nn=1Enexp（jn）（1）

为了校准阵列元件的复激励失真，本文将方程（1）分为2部分：

E=E1+E2=E1exp（j1）+E2exp（j2）=（E1cos1+E2cos2）+j（E1sin1+E2sin2）（2）

E1和1为分组内相位改变单元的合成辐射场的幅度与初始相位。E2和2为组内相位不变单元的合成辐射场的幅度与初始相位。令相位不变单元的功率为P2，P2=E22，可以通过关闭相位改变单元来测量。

根据式（2），天线总辐射场功率P0可表示为：

P0=E2=（E1cos1+E2cos2）2+（E1sin1+E2sin2）2=E21+E22+2E1E2cos（1-2）（3）

令φ=1-2，则式（3）可进一步写为：

P0=E21cos2φ+E21sin2φ+E22+2E1E2cosφ=（E1cosφ+E2）2+E21sin2φ（4）

然后，本文将分组内所有相位改变单元的相位偏移设为π/2；那么，相应的阵列功率Pπ/2可以写成：

Pπ/2=E21+E22-2E1E2sinφ=E21cos2φ+E21sin2φ+E22-2E1E2sinφ=（E1sinφ-E2）2+E21cos2φ（5）

根据方程（4）和（5），2个未知数E1sinφ和E1cosφ可以推导如下：

E1cosφ=P0-Pπ/2-2P2+M4P2

E1sinφ=P0-Pπ/2+2P2-M4P2（6）

E1cosφ=P0-Pπ/2-2P2-M4P2

E1sinφ=P0-Pπ/2+2P2+M4P2（7）

上式中，M=-4P22-P20-P2π/2+2P0Pπ/2+4P0P2+4P2Pπ/2。

与传统的旋转矢量法一样，本方法有方程（6）和（7）2个可能的解。如果分组内相位改变单元的合成辐射场幅度E1小于相位保持单元的合成辐射场幅度E2，则可以消除这组解的二义性［8］。

根据方程（6）和（7），第N个分组内相位改变单元的合成辐射场相对全阵初始辐射场的幅度和相位可表示为：

A1N=E1exp（j1）E1exp（j1）+E2exp（j2）=E1exp（xjφ）E1exp（jφ）+E2（8）

上式中，E1和1可通过下式直接计算得出：

E1=E12cos2φ+E12sin2φ（9）

φ=arctanE1sinφE1cosφ（10）

根据上述方法，本文可以逐步计算得到其他分组相位变化单元的总辐射场对全阵初始辐射场的相对幅度和相对相位。联立N个方程，该方程组可用矩阵形式表示为：

HN×N·A1A2AN=A11A12A1N（11）

上式中，A1，A2，…，AN为第N个天线单元辐射场相对于全阵初始总辐射场大小的比值，A11，A12，…，A1N为已求得的N个不同分组在移相量为0°时组内相位改变单元的合成辐射场相对全阵初始合成辐射场的比值。矩阵H被称为分组矩阵，矩阵的每行为一个分组，矩阵元素为1的单元为分组内改变相位的单元，矩阵元素为0的单元相位保持不变，但为了求解式（11），矩阵H应可逆。如果阵列单元的数目N更大，可以使用低阶的合适的可逆矩阵P来构造块对角矩阵H来作为分组矩阵。

解式（11），可解得单元相对阵列总体信号的相对幅相分布A1，A2，…，AN为：

A1A2AN=H-1N×N·A11A12A1N（12）

由阵面的幅相分布可得到每个通道所需的校准补偿幅相值，从而实现阵面标校。

2 仿真结果

本文利用HFSS软件对校准方法进行仿真验证。仿真阵列为12×12的方阵，单元服从等幅同向分布，仿真开始为阵列单元设置随机初始激励［9］。本次仿真使用的分组矩阵H为块对角矩阵，矩阵P为一个36阶的幺模矩阵：

H=PO

P

OP（13）

根据分组矩阵模拟测量每组单元相位改变前后远场功率，可计算得出阵面相对幅相分布。图1和图2为计算得出的阵面相对幅相分布与实际幅相分布对比图，可以看出估计结果与实际值可以较好地吻合，验证了分组功率校准方法的可行性。

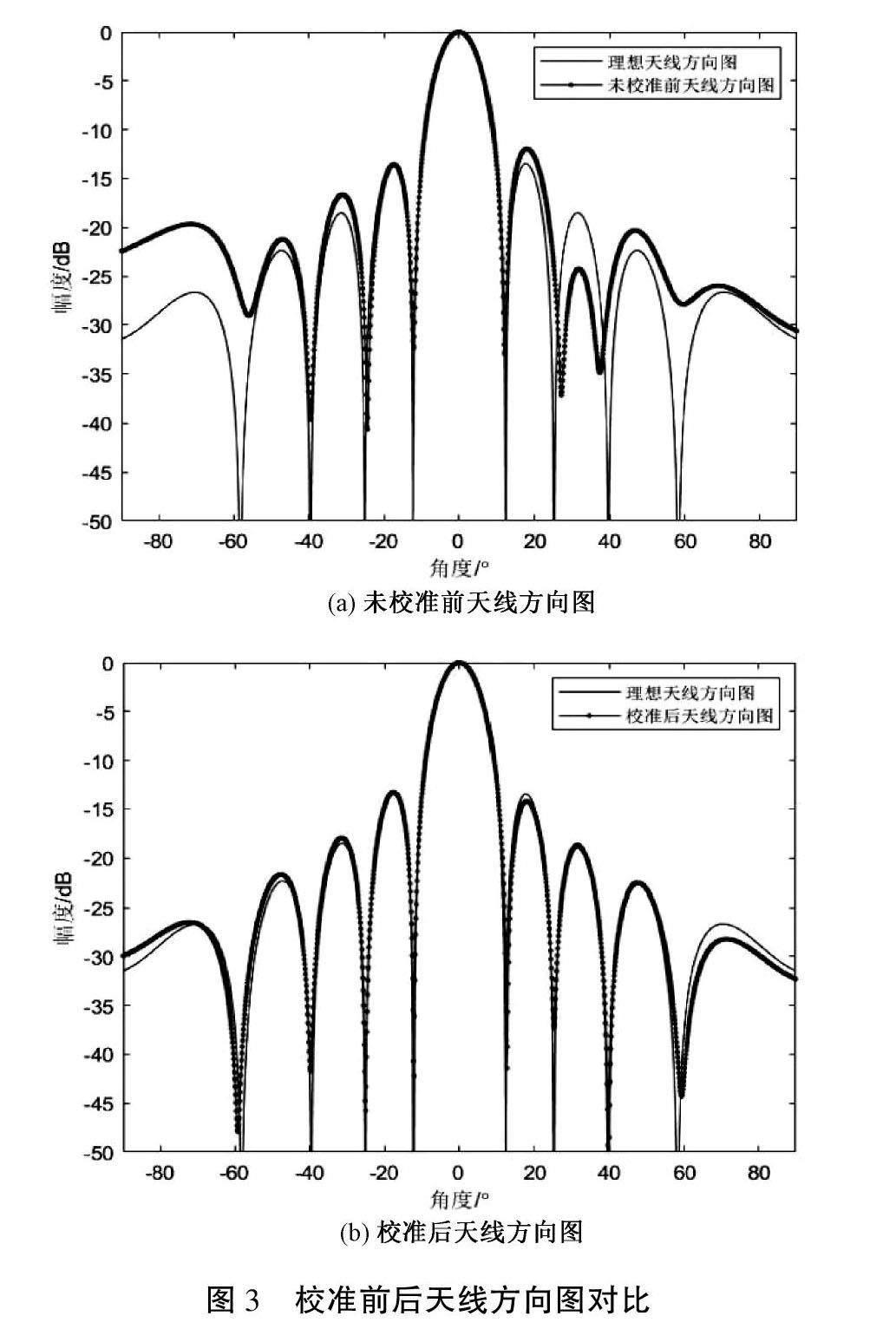
校准前后的天线方向图与理论值对比如图3所示。从图中可以看出使用本文方法校准后的天线方向图与理想方向图吻合较好，天线主瓣与理论值一致，副瓣明显降低，达到了校准效果。

3 结语

本文提出了一种只需功率测量的相控阵天线分组校准方法，并给出了不同移相误差状态时的幅相均方根误差。对12×12元阵列的仿真结果表明：使用该方法校准后的天线方向图与理想方向图吻合较好，天线主瓣与理论值一致，副瓣明显降低，达到了校准效果。

参考文献

［1］高铁，王金元.大型有源相控阵校准的MCM法及其误差分析［J］.微波学报，2002（1）：6-10，19.

［2］张云.相控阵天线近场幅相校准［J］.中国电子科学研究院学报，2007（6）：611-614.

［3］郑雪飞，高铁.相控阵天线中场校正技术研究［J］.微波学报，2005（5）：22-25.

［4］敬红勇，李正军，田步宁.一种基于功率测量的相控阵天线校准方法［J］.空间电子技术，2009（3）：      66-68.

［5］刘明罡，冯正和.分组旋转矢量法校正大规模相控阵天线［J］.电波科学学报，2007（3）：380-384.

［6］齐宏业，杜彪，位静云，等.基于三相幅度测量的相控阵天线快速校准方法［J］.现代雷达，2019（8）：56-59.

［7］王迪，王雪梅，何岷，等.弹载相控阵天线“最小二乘法：伪Hadamard矩阵”联合校准［J］.系统工程与电子技术，2020（2）：271-276.

［8］HE G L，GAO X，ZHOU H.Fast phased array calibration by power-only measurements twice for each antenna element［J］.International Journal of Antennas and Propagation，2019（2）：1-10.

［9］李亚麟，樊迅，胡波，等.天线校准误差建模及对开环波束赋形技术的影响［J］.电讯技术，2010（3）：45-48.

（编辑 王雪芬）

Invention relates to a grouping calibration method for phased array antennas with only power measurement

WANG  Fuyu， CHEN  Wenjun， LU  Qing

（The 724th Research Institute of China Shipbuilding Group Corporation， Nanjing 210000， China）

Abstract：  A large phase error in the transceiver channel of phased array antenna will result in distortion of radiation pattern， decrease of antenna gain and increase of sidelobe. In order to obtain the ideal antenna pattern， this paper presents a method of group calibration of phased array antenna based on power measurement. Besides measuring the total array power of primary array， the relative amplitude and phase distribution of array elements can be determined only by one phase shift and two power measurements. In order to make the synthetic radiation field signal change obviously in the calibration process， the method uses the grouping matrix to group the array， changes the phase of several units at the same time during calibration， and calculates the amplitude and phase distribution of all units by substituting the measured power values into the formula. The simulation results of the 12×12 element array show that the level of the side lobe of the antenna pattern is significantly reduced after calibration with this method， and the main lobe of the antenna pattern is basically consistent with the theoretical value， and the calibration effect is achieved.

Key words： antenna calibration; phased array antenna; grouping calibration; power measurement