罗田水库—铁岗水库输水隧洞输水能力及糙率敏感性
2024-07-06杨旭良谢良涛周宁李娇娜胡晗
杨旭良 谢良涛 周宁 李娇娜 胡晗


摘要:输水隧洞的输水能力是由隧洞的糙率和沿程建筑物的局部水头损失共同决定的。采用一维、三维耦合计算模型对罗因水库—铁岗水库输水隧洞的输水能力进行了研究,并考虑输水管道内壁淡水壳菜滋生对管道输水能力的影响,进行了糙率敏感性研究。研究结果表明:① 在隧洞糙率n取0.015 0的设计条件下,进水口流量可达到30.12 m3/s,出水口流量可达到12.12 m3/s,满足设计要求;② 糙率n与输水隧洞总水头损失大约呈线性关系,隧洞糙率每增加0.000 5,相应输水隧洞总水头损失增加约0.17~0.19 m;③ 当糙率增加到0.015 5时,隧洞输水能力已不能满足设计供水流量要求。
关键词:输水隧洞; 输水能力; 水工水力学; 数值模拟; 糙率
中图法分类号: TV135
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2024.S1.042
0引 言
罗田水库—铁岗水库输水隧洞工程(以下简称“罗铁隧洞”)是珠江三角洲水资源配置工程在深圳境内配套项目之一。工程主要建筑物包括:进水口、出水口、输水干线、与深圳分干线连通隧洞,至罗田水厂、五指耙水厂、长流陂水厂分水支线及3条检修交通洞,罗田水库应急放空洞等。工程布置如图1所示。
在工程设计阶段需要对罗铁隧洞的输水能力进行预测。输水隧洞的输水能力受隧洞的糙率和沿程建筑物的局部水头损失共同影响。在输水隧洞的设计中,糙率为非常重要的参数,直接影响输水隧洞的过水能力。精确的糙率值往往需要通过现场原型观测进行反演计算来获取[1-3]。在设计阶段需要根据以往的工程经验对糙率进行估计,并通过糙率对输水能力的敏感性分析来对设计方案进行评估。但是,在输水隧洞的设计阶段很难预估沿程一系列建筑物的局部水头损失,特别是对于包含复杂的进、出水建筑物和多个沿程分水支线的输水隧洞。
设计阶段对输水隧洞输水能力的预测,往往通过水力学计算、一维数学模型计算和水工模型试验,而这3种方法均有其不足。水力学方法[4]和一维数学模型[5-6]可以准确预估长距离输水隧洞的沿程水头损失,而无法精确预估复杂的进、出水建筑物和沿程水工建筑物造成的局部水头损失。罗铁隧洞采用塔式进水口和塔式出水口,且进水口塔中还设置了分层取水叠梁门,因此难以通过水力学方法和一维数学模型进行准确计算。大比尺水工模型试验可以精确测量进、出水建筑物和沿程水工建筑物造成的局部水头损失,而由于缩尺效应的影响,很难测量长距离输水隧洞沿程水头损失。针对这些不足,本次研究采用一维、三维耦合模型进行计算,既能通过一维模型准确计算隧洞主线的沿程水头损失,又能通过三维模型针对一系列复杂水工建筑物计算其产生的局部水头损失。
1模型构建
上下游库区及进、出水口局部流场采用VOF三维模型进行计算,重点关注库区流场及进、出水口的局部水头损失。使用雷诺平均Navier-Stokes方程结合湍流模型进行计算。
连续性方程:
xiuiAi=0(1)
动量方程:
uit+1VFujAjuixj=-1ρpxi+gi+fi(2)
式中:ui为x、y、z方向的速度;Ax、Ay、Az为计算单元x、y、z向面积;VF为各计算单元内液体的体积分数;ρ为液体密度;p为压强;gi为重力加速度;fi为雷诺应力。
为了准确计算紊流,选择RNG k-ε模型作为紊流计算模型。
隧洞主线及分水支线采用一维水力计算模型进行模拟,重点研究沿线水力损失及隧洞糙率敏感性。一维水力计算模型基于圣维南方程组,通过反映质量守恒定律的水流连续方程和反映动量守恒定律的运动方程进行联立求解,其计算表达式如下:
At+1BQt=qBut+xαu2A+gAZx+gSf+quA=0(3)
式中:A为过水断面面积;Q为断面流量;Z为断面水位;x和u为输水隧洞水平和横向方向距离;g为重力加速度;t为时段计算步长;α为流速系数:Sf为水力学坡比;B为断面水面宽度。采用Preissman四点加权差分方程对一维水动力学模型进行求解。
罗铁隧洞输水干线长21.68 km,过流断面直径5.2 m。正常运行期间,从罗田水库取水,沿程经过罗田水厂支线、五指耙水厂支线和长流陂水厂支线分水,最终向铁岗水库供水。设计工况下,罗田水库和铁岗水库水位差为3.08 m,输水隧洞罗田水库进水口进水流量30 m3/s,进水口水位28.09 m,沿线分别向罗田水厂、五指耙水厂、长流陂水厂分水,相应分水设计流量分别为8.1,3.5 m3/s和6.4 m3/s,铁岗水库出水口出水流量12 m3/s。罗铁隧洞一维、三维耦合计算模型的拓扑结构如图2所示。
进水口采用塔式,位于罗田水库内,进水塔顺水流向依次布置拦污栅段、叠梁门段、进水仓段和喇叭口段、闸门段等,如图3所示。
出水口同样采用塔式,顺水流向依次布置渐变段、闸门段、喇叭口段、拦污栅段和出水渠段,如图4所示。
2计算结果及分析
2.1局部水头损失
局部水头损失是指由局部边界急剧改变导致水流结构改变、流速分布改变并产生旋涡区而引起的水头损失。对于罗铁隧洞而言,进水口段和出水口段的局部水头损失定义为:从罗田水库进水口引水渠之前到进水口测压环面、出水口测压环面到铁岗出水口出水渠之后的水头损失。局部水头损失系数定义为局部水头损失与计算部位平均流速水头的比值。
通过一维、三维耦合模型计算得到了设计工况下(隧洞进口流量30 m3/s,各支线分水流量合计18 m3/s,隧洞出口流量12 m3/s),进水口段、出水口段的局部水头损失,列于表1。
由表1可知,设计水位工况下,在进水口放置3节叠梁门将增加的水头损失约为0.160 m。
该工况下,将沿途支线分水产生的局部水头损失计算结果列于表2。
由表1~2可知,设计工况下,由进、出水口和沿途支线分水产生的局部水头损失之和为0.289 m。
2.2沿程水头损失
沿程水头损失是指水流在隧洞中克服管线摩擦阻力而损失的水头,糙率的选择是计算输水隧洞沿程水头损失的关键。
取隧洞糙率n=0.015,计算输水隧洞输水干线沿程水头损失。在设计工况下,从进水口(圆形隧洞开端)至出水口(圆形隧洞末端)沿程各分段水头损失如表3所列。可知,设计工况下,隧洞输水干线沿程水头损失之和为2.762 m。
2.3输水能力分析
通过模型计算得知,在隧洞糙率n取0.015,设计条件下,即进水口水库水位28.09 m,出水口水库水位25.00 m,罗田水厂支线设计流量为8.10 m3/s,五指耙水厂支线设计流量为3.50 m3/s,长流陂水厂支线设计流量为6.40 m3/s时,进水口流量可达到30.12 m3/s,出水口流量可达到12.12 m3/s,可以满足设计要求。
2.4隧洞糙率敏感性研究
由于珠江三角洲地区输水管道中普遍容易附着生长一种淡水壳菜,导致管道糙率在运行一段时间后发生变化[7-8]。随着运行时间的增加和管道内壁淡水壳菜的繁殖,管道糙率会逐步增加;经过停水检修期,附着在隧洞内壁的淡水壳菜死亡和脱落,对管道内淡水壳菜清理后,管道糙率又恢复到或接近最初的糙率[9]。因此,需在一定范围内选择管道糙率。
该工程全线采用压力钢管,糙率受钢管内防腐涂层及运行后生物附着和表面腐蚀等因素影响,其中,生物附着物对糙率的影响较大。考虑到工程运行初期管道内壁尚未生长淡水壳菜,根据SL 279-2016《水工隧洞设计规范》[10],钢管糙率可取0.011 0~0.013 0。输水管道内壁淡水壳菜滋生严重影响管道输水能力,除定期清理外,尚无彻底解决措施。据国内部分工程统计资料[11](表4),淡水壳菜附着使管道糙率增加约16.06%~46.49%。
参照相关规范及同类工程经验,该工程糙率取值范围定为0.014 0~0.016 0。
研究思路为,按设计工况设置固定的下游铁岗水库水位,给定上游来流流量30 m3/s,给定沿线罗田水厂、五指耙水厂、长流陂水厂分水支线流量分别为8.1,3.5,6.4 m3/s,反算上游罗田水库库水位,如果计算得到的水位低于或等于28.09 m,则表示该设计方案的隧洞输水能力可以满足要求;否则认为该设计方案的隧洞输水能力不能满足要求。
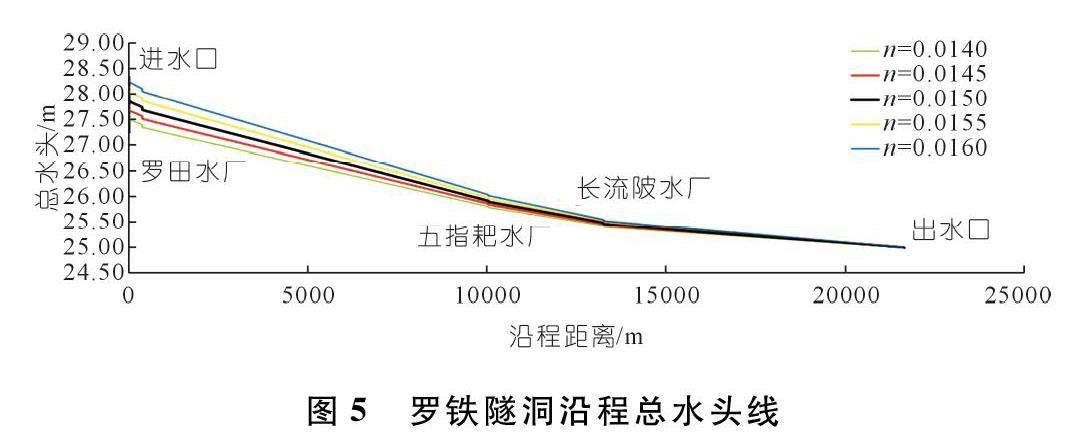
通过一维、三维耦合计算模型计算罗铁隧洞主线管道取不同糙率系数时的总水头沿程变化曲线。计算水流条件为:铁岗水库水位为25.00 m,隧洞进、出口流量及各分水口流量均为设计流量,成果如图5所示。
水流在行进过程中由于沿程水头损失呈现逐渐下降趋势,在经过进、出水口和沿途支线分水后,由于局部水头损失,总水头均突然下跌。随着隧洞主线管壁糙率增大,上游水位随之升高,曲线也相对陡峭。当糙率取为0.015 0时,输水隧洞总水头损失为3.051 m,小于罗田水库与铁岗水库设计水位差(3.08 m),能满足设计供水流量要求。当糙率增加到0.015 5时,输水隧洞总水头损失为3.239 m,大于罗田水库与铁岗水库设计水位差(3.08 m),在设计上下游库水位条件下,如沿程各支线取水量保持不变,则进水口流量为29.50 m3/s,出水口流量为11.50 m3/s,不能满足设计供水流量要求。
在上述输水流量条件下,隧洞不同糙率条件下的总水头损失汇总如图6所示。
可知,糙率n与输水隧洞总水头损失大约呈线性关系,隧洞糙率每增加0.000 5,相应输水隧洞总水头损失增加约0.17~0.19 m。
3结 论
本文采用一维、三维耦合计算模型研究了罗铁隧洞的输水能力和糙率敏感性,研究结果表明:① 在隧洞糙率取为0.015 0,设计条件下,进水口流量可达到30.12 m3/s,出水口流量可达到12.12 m3/s,可以满足设计要求。其中,由进、出水口和沿途支线分水产生的局部水头损失之和为0.289 m,隧洞输水干线沿程水头损失之和为2.762 m。② 糙率n与输水隧洞总水头损失大约呈线性关系,隧洞糙率每增加0.000 5,相应输水隧洞总水头损失增加约0.17~0.19 m。③ 当糙率增加到0.015 5时,在设计上下游水库水位条件下,隧洞输水能力将不能满足设计供水流量要求。
参考文献:
[1]王明亮.水动力学模型在引水隧洞糙率反推及过流能力复核中的应用[J].东北水利水电,2020,38(7):34-37,72.
[2]李辉.基于原型观测试验的引水隧洞糙率反推计算及过水能力复核方法探讨[J].地下水,2017,39(3):142-144.
[3]徐琳,方旭.基于水力学模型的引水隧洞糙率反推计算研究[J].中国水能及电气化,2015(11):51-53.
[4]沈国梁.基于水动力学方法的输水隧洞糙率反推及过水能力复核分析[J].黑龙江水利科技,2021,49(4):131-133.
[5]陈文熙.基于一维非恒定流数学模型的辽宁省引水隧洞糙率推求研究[J].水利技术监督,2015,23(4):35-38,41.
[6]王常红.长距离输水隧洞水力特性数值模拟研究[D].天津:天津大学,2008.
[7]李代茂.淡水壳菜对输水建筑物输水能力的影响研究[J].给水排水,2009,45(增1):94-96.
[8]秦晓川.珠江三角洲水资源配置工程输水隧洞糙率取值范围研究[J].广东水利水电,2021(4):31-34.
[9]田勇,张爱静,王树磊,等.输水工程中淡水壳菜生物污损影响及防治对策研究[J].水生态学杂志,2020,41(1):110-116.
[10]中华人民共和国水利部.水工隧洞设计规范:SL279-2016[S].北京:中国水利水电出版社,2016.
[11]冯文涛.淡水壳菜对东深供水工程司马有压箱涵糙率影响分析[J].甘肃水利水电技术,2016,52(4):10-13.
(编辑:郭甜甜)
