汽车碰撞速度与年龄因素对下肢损伤影响
2024-07-05陈凯

摘 要:本研究旨在探讨年龄因素对行人下肢损伤的影响,以提高行人保护水平。基于CIDAS(China in-depth accident study)数据库,筛选了2017-2022年的16起真实行人碰撞案例。利用PC-Crash软件重建事故,获取边界条件,并将其导入车辆-行人下肢有限元碰撞模型进行损伤重建。通过逻辑回归模型分析,得到不同碰撞速度下,各年龄段的损伤参数和下肢损伤风险预测模型。研究结果显示,各年龄段的下肢长骨损伤阈值和耐受极限存在差异。本研究为行人保护法规及下肢损伤评估指标制定提供了重要数据支撑。
关键词:汽车-行人 年龄-速度 事故重建 AIS3+重伤风险 逻辑回归 有限元
世界卫生组织《2023年道路安全全球现状报告》指出,尽管全球道路交通死亡人数每年下降5%,但行人和其他弱势道路使用者的死亡风险正在上升[1]。据胡林等人研究[2],下肢损伤在所有AIS2+损伤中占32.6%,在所有伤情中比例为32.8%。下肢损伤虽少致命,但给社会带来巨大财产损失,因此加强行人下肢保护至关重要。
在行人-车辆碰撞事故中,行人下肢的损伤程度受多种因素影响。研究表明,撞击时的速度以及行人的年龄是影响行人下肢损伤的最重要因素[3-4]。目前,Klinich等人[4-5]的研究围绕事故中下肢受损因素对其Abbreviated Injury Scale (AIS)等级的影响,结果表明,随着碰撞速度的增加、行人年龄的增长以及行人身高或车辆重心位置的上升,行人下肢受到AIS2级及以上损伤的风险也会增加。Kunitomi[6]则致力于模拟行人有限元碰撞仿真分析,探究了不同速度冲击下的乘用车前端结构变化对行人下肢骨折的效应。行人年龄对下肢损伤有重要影响。随着年龄增长,下肢承受应力应变减小,更易受损。杨济匡等人[7]发现,随着年龄的增长,腿部长骨对拉力和压力的承受能力有差异,导致骨折的风险随年龄递增而上升。Klein等人[8]开发了包含年龄、性别、股骨结构和身体质量指数的股骨有限元模型,模拟行人和车辆碰撞,发现不同年龄段碰撞模型是下肢损伤存在差异。
尽管有很多学者对行人下肢损伤做过研究,但很少有研究考虑到速度、年龄对下肢损伤的综合影响。本文基于CIDAS数据库中的16个行人下肢损伤案例,运用PC-Crash事故重建技术,获取了行人与汽车相撞时的相对速度以及行人相对汽车前部的姿态角度等关键边界条件,将所述边界条件整合进已构建的车-行人下肢碰撞有限元模型中模拟碰撞,进行损伤重建。通过分析行人下肢损伤参数(如股骨和胫腓骨的弯矩和剪切力),结合逻辑回归模型,探讨了行人年龄、长骨损伤参数与AIS3+重伤风险之间的相关性,并深入研究年龄因素对下肢损伤在不同碰撞速度下的影响[4]。
1 数据模型
在挑选的16起行人下肢损伤案例基础上,利用PC-Crash事故重建技术获取关键的边界条件,进行车辆-行人有限元碰撞仿真,获取行人下肢股骨和胫腓骨损伤参数,并开展行人年龄、长骨损伤参数与AIS3+重伤风险的相关性分析。
1.1 车辆与下肢碰撞模型的建立与验证
1.1.1 具有年龄特征的行人下肢有限元模型
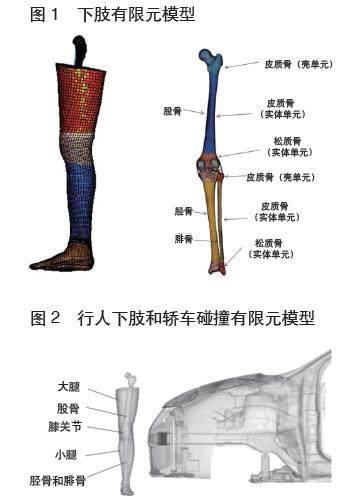
研究表明,年龄是影响行人下肢重伤和长骨骨折风险的关键因素[9]。随着年龄增长,骨骼失效应力减小,耐受极限降低,骨折和重伤风险增加。这主要体现在下肢材料和骨骼结构上。本文采用龙永程[10]建立的下肢有限元模型进行研究。该模型包括皮肤、肌肉、膝关节韧带和长骨(由股骨、胫骨和腓骨),如图1。长骨骨干部位的皮层骨与端部的海绵骨在材质属性上有显著差异,这是引起长骨骨折的重要原因。本文可根据年龄对下肢有限元模型中膝关节力学性能和骨骼几何结构的影响对材料参数进行调整[11]。
1.1.2 汽车-行人碰撞模型建立及验证
为进一步分析年龄,长骨弯矩和剪切力等损伤参数和AIS3+重伤风险的相关性,验证有限元模型的有效性。本文将有限元模型中的保险杠距地高度等参数进行调整,车头数据参照汽车对行人碰撞保护法规方法,将汽车前保险杠距离地面的高度设为540 mm,前保险杠垂直冲击面的宽度定为120 mm。为降低模拟时间成本,用等效的质量块代替了车辆A柱之后的区域,在不改变车辆整体重量及其重心位置的基础上,在车尾部分加上了集中的重量块,并与后端梁实现了刚性连接[10],如图2。
本文所有的真实事故案例均来自CIDAS数据库,由于每起事故的行人参与方身高体重都不同,本文通过运用Hypermesh软件内的Hypermorph功能,对行人下肢有限元网格进行调节以适应各个年龄段长骨的尺寸变化,模拟人体自身体重对股骨设置加载力,下肢与地面的摩擦因数为0.65。
选用公式(1)调整下肢模型的高度使之配合标准,以及利用公式(2)进行股骨头受力的调整。实验以成年人中位数尺寸为行人标准体型,该体型的标准身高与体重分别为1.75米和78公斤[10-11]。
(1)
式中:H是事故中受害行人的身高,是模型中下肢的实际长度;
H0标准人体模型的身高;是初始模型的下肢长度。
(2)
式中:F是事故中施加在股骨上的力模型,W是被撞行人的重量;
F0是原设定的股骨承受的力,取400N;W0是初始的人体重量。
针对具体案例特征,采用PC-Crash分析工具,对行人下肢与小轿车碰撞案例进行重建,获取相对碰撞速度等关键边界条件。随后,将这些参数导入到轿车-行人有限元碰撞仿真模型,进行损伤重建。图3展示了模型仿真的运动响应,行人下肢首先与轿车保险杠接触,之后与发动机罩发生碰撞。图4的对比显示,模拟撞击位置与现实汽车受损部位高度一致,证明了该有限元模型在模拟分析中的高仿真性和有效性。
1.2 统计方法
本文采用逻辑回归的方法来解释行人年龄、碰撞速度和下肢长骨损伤参数(长骨弯矩和剪切力)与下肢AIS3+重伤和骨折的关系,并且构建逻辑回归模型:
(3)
其中P为发生概率,x为考察变量,系数α和β为模型中尚待评估的系数,并可以通过最大似然估计的方法来求解,本文根据设定的P值显著性标准(0.05)来判断变量间的相关性是否统计上显著:P值小于0.05表明相关性显著,否则不显著[12]。
2 结果分析
2.1 年龄-长骨损伤参数-重伤风险的相关性分析
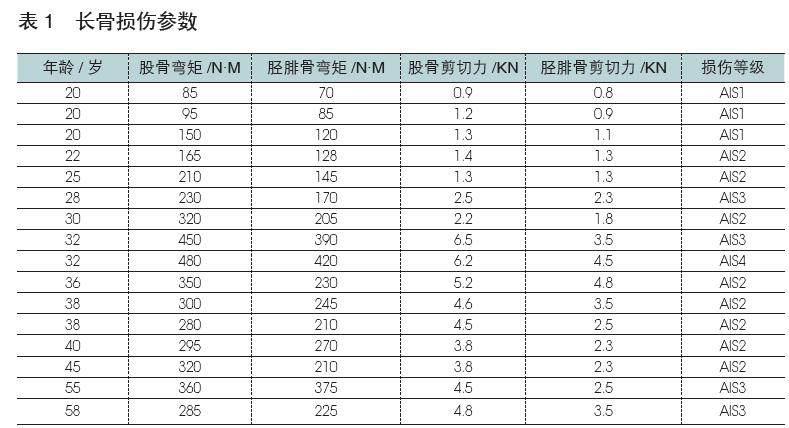
随着行人年龄增长,下肢的骨折的极限应变和应力会逐步降低,骨折发生的可能性相应增加[7]。本文依据院门诊记录对行人下肢的损伤描述,利用AIS损伤等级对下肢损伤进行评判,分类为轻伤(AIS0-2级)与重伤(AIS3级及以上)[3-4]。基于真实案例,使用PC-Crash软件重建关键边界条件,导入车辆-行人下肢有限元碰撞模型进行损伤分析。通过仿真,得到股骨和胫腓骨的弯矩和剪切力等参数,并分析行人年龄-长骨损伤参数-AIS3+重伤风险的相关性。在16起事故案例中,仿真得到股骨和胫腓骨的弯矩和剪切力等损伤参数,如表1所示。
根据仿真导出的数据结果可知,样本股骨和胫腓骨弯矩平均值分别为273 N·M和3218 N·M,剪切力平均值分别为3.4 KN和2.4 KN。根据样本数据,利用公式(9)构建了年龄-长骨损伤参数-行人下肢严重损伤AIS3+的逻辑回归方程,其中x为考察变量,系数α、β和为待估计参数,并可以通过最大似然估计的方法来求解,由表2和表3统计数据表明,P值小于0.05,即验证了长骨(股骨和胫腓骨)损伤参数与下肢严重损伤之间存在显著的相关性。
根据股骨和胫腓骨的弯矩逻辑回归分析结果,构建了年龄-长骨弯矩-AIS3+重伤风险的三维可视图,如图5所示,可以预测在不同年龄和不同长骨弯矩值情况下对AIS3+重伤风险概率进行预测,由图可见随着年龄、股骨和胫腓骨弯矩值的变大,下肢重伤风险越来越大,通过图5(a)和图5(b)的对比发现在相同年龄条件下,胫腓骨弯矩和股骨弯矩对行人下肢重伤风险的影响存在差异。
当下肢重伤损伤风险概率为50%时,对应的长骨弯矩和年龄分布如图6所示,随着年龄变大,长骨弯矩值逐渐变小,当行人年龄为30岁,下肢发生重伤概率为50%时对应行人股骨弯矩值为396 N·M,胫腓骨弯矩值为315 N·M,当行人年龄为50岁,下肢发生重伤概率为50%时对应行人股骨弯矩值为300 N·M,胫腓骨弯矩值为244 N·M,在具有相同重伤风险概率下,股骨弯矩值始终要大于胫腓骨弯矩值。
根据股骨和胫腓骨的剪切力逻辑回归分析结果,构建了行人年龄-长骨剪切力-AIS3+重伤风险的三维可视图,如图7可见随着年龄、股骨和胫腓骨剪切力值的变大,下肢重伤风险越来越大,通过图7(a)和图7(b)的对比发现在相同年龄和剪切力值条件下,胫腓骨剪切力对行人下肢重伤风险的影响要大于股骨剪切力对下肢重伤风险的影响。
当行人下肢重伤风险概率为50%时,其长骨剪切力和年龄分布如图8,随着年龄变大,长骨剪切力值逐渐变小,当行人年龄为30岁,下肢发生重伤概率为50%时对应行人股骨剪切力值为5.45 KN,胫腓骨剪切力值为4.25 KN,当行人年龄为50岁,下肢发生重伤概率为50%时对应行人股骨剪切力值为4.2 KN,胫腓骨剪切力值为2.5 KN,在具有相同重伤风险概率时,股骨剪切力值始终要大于胫腓骨剪切力值。
以上数据与Kerrigan等的研究结果一致,他们测得30-50岁人群的股骨弯矩和胫骨弯矩分别为412±102 N·M和310±50 N·M,误差为6%,误差在正常范围内[13]。同时,模拟的结果也与Martens等人[14]记录的股骨弯曲耐受极限(373±84 N·M)持平。胫腓骨弯矩和剪切力值也符合Nyquist等人[15]试验测量年龄段为30-50岁时弯矩(317±88 N·M)和剪切力(4.1±1.2) KN的范围,与试验测量的胫骨剪切力相比低了13.8%,在正常误差范围内。与Kress等人[16]测量出年龄为50岁时股骨弯矩数据(320 N·M)和剪切力数据(3-10 KN)吻合,但胫骨弯矩值与Mo Fuhao等人[17]对年龄为50岁的胫骨骨干测试数据339 N·M相比低了28%,这由于实验加载位置不同,得出来的数据会有差距,胫骨中段对抗弯曲的能力要优于其近端或远端1/3区域的能力,另外本研究模型简化了膝盖的韧带复杂结构,这个做法也降低了模型的生物仿真性,并可能进一步影响到了实验结果的信准度。针对这一点,未来的相关研究需提高对生物仿真性的要求[4]。
3 结语
本文以CIDAS数据库记录的16起案例为研究基础,利用PC-Crash软件和车辆-行人下肢有限元碰撞模型,建立行人年龄-长骨损伤参数-AIS3+重伤风险的三维可视图,可得出结论:
由对应的长骨弯矩和剪切力与年龄分布图可以发现,当下肢重伤损伤风险概率为50%时,行人年龄为30岁,对应行人股骨弯矩值为396 N·m,胫腓骨弯矩值为315 N·m,对应行人股骨剪切力值为5.45 KN,胫腓骨剪切力值为4.25 KN;行人年龄为50岁,对应行人股骨弯矩值为300 N·M,胫腓骨弯矩值为244 N·M,对应行人股骨剪切力值为4.2 KN,胫腓骨剪切力值为2.5 KN,不同年龄段胫腓骨和股骨的弯矩和剪切力值对行人下肢重伤风险的影响存在差异。
基金项目:湖南省教育厅资助科研项目(22C1083),工程车辆安全性设计与可靠性技术湖南省重点实验室(长沙理工大学)开放基金资助项目(2020YB05)资助。
参考文献:
[1] WHO. Global status report on road safety 2023[EB/OL].https://www.who.int/teams/social-determinants-of-health/safety-and-mobility/global-status-report-on-road-safety-2023.
[2] Jing Huang, Yang Peng, Lin Hu. A multilayer stacking method base on RFE-SHAP feature selection strategy for recognition of drivers mental load and emotional state. Expert Systems with Applications, 2024, 238: 121729.
[3]陈凯.行人年龄和碰撞速度对行人下肢损伤的影响研究[D].长沙:长沙理工大学,2019.
CHEN K. Effects of Pedestrian Age and Collision Speed on Pedestrian Lower Limb Injury[D]. Changsha: Changsha University of Science & Technology, 2019.
[4]胡林,陈凯,黄晶,等.年龄因素对行人下肢损伤的影响研究[J].机械工程学报,2020,56(02):106-120.
HU L, CHEN K, HUANG J, et al. Study on the Effect of Age on the Lower Extremity Injury of Pedestrians[J]. Journal of Mechanical Engineering, 2020,56(02):106-120.
[5] K D Klinich,L W Schneider. Bio-mechanics of Pedestrian Injuries Related to Lower Extremity Injury Assessment Tools: A Review of the Literature and Analysis of Pedestrian Crash Database [D]. Michigan: University of Michigan Transportation Research Institute, 2003.
[6] Kunitomi S, Yamamoto Y, Kato R, et al. The Development of the Lower Extremity of a Human Fe Model and the Influence of Anatomical Detailed Modelling in Vehicle-to-pedestrian Impacts[J]// International Research Council on Biomechanics of Injury(IRCOBI). Antwerp, Belgium:2017 IRCOBI Conference Proceedings, Oct 21 2017, 17-62.
[7] Yang J. Review of injury biomechanics in car-pedestrian collisions[J]. International journal of vehicle safety, 2005, 1(1): 100-117.
[8] Klein K F, Hu J, Reed M P, et al. Validation of a Parametric Finite Element Human Femur Model[J]. Traffic Injury Prevention, 2017, 18(4):420-426.
[9]王丙雨,聂进,DIETMAROTTE,等.碰撞速度和行人年龄对下肢严重损伤风险的影响[J].汽车安全与节能学报,2018,9(1):25-31.
[10]龙永程.年龄因素对行人下肢有限元建模及损伤的影响研究[D].长沙:湖南大学,2016.
[11] Weaver A A, Schoell S L, Nguyen C M, et al. Morphometric Analysis of Variation in the Sternum with Sex and Age[J]. Journal of Morphology, 2014, 275(11): 1284-1299.
[12] Kulas J T, Roji R G P P, Smith A M. IBM SPSS Essentials: Managing and Analyzing Social Sciences Data[M]. John Wiley & Sons, 2021.
[13] Kerrigan J R, Bhalla K S, Madeley N J, et al. Experiments for establishing pedestrian-impact lower limb injury criteria[C]. //SAE 2003 World Congress (SP-1740). 2004.
[14] Martens M, Van A R, De M P, et al. Mechanical behaviour of femoral bones in bending loading[J]. Journal of Biomechanics, 1986, 19(6): 443-454.
[15] Nyquist G W. Facial Impact Tolerance and Response[C]// Proc. of the, Stapp Car Crash Conference. 1986:3-11.
[16] Kress T A, Snider J N, Porta D J, et al. Human Femur Response to Impact Loading[C]//Proceedings of the International Research Council on the Biomechanics of Injury conference. International Research Council on Biomechanics of Injury, 1993, 21: 93-104.
[17] Mo F, Arnoux P J, Jure J J, et al. Injury tolerance of tibia for the car–pedestrian impact[J]. Accident Analysis & Prevention, 2012, 46: 18-25.
