一种磁耦合型M形屈曲梁压电俘能器研究

栾浩 田立斌 陈坤铭 丁晓亮 沈辉

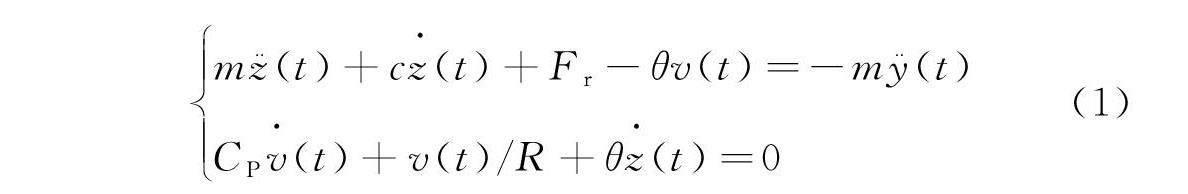
摘要：为了提高压电俘能器在低频弱振动环境下的俘能效率，在M形屈曲梁压电俘能器（MEH）的基础上引入非线性磁力，提出了一种磁耦合型MEH，建立了系统的集总参数模型，并基于M形屈曲梁结构的非对称性，通过实验测量并拟合了M形屈曲梁的非线性恢复力，探究了非线性磁力对系统性能的影响。仿真和实验结果表明，磁耦合型MEH具有更宽的工作频带，在0.5 g加速度激励下达到了8.3 Hz（5.5 Hz～13.8 Hz），比无磁耦合时的MEH提高了12.2%；磁耦合型MEH具有更低的跨阱阈值，在0.15 g加速度激励下可以实现大振幅周期运动。

关键词：压电俘能器；M形屈曲梁；非线性；双稳态

中图分类号：TN384文献标志码：A

随着微电子技术和低功耗技术的不断进步，无线传感器向着微型化、智能化、低功耗化等方向飞速发展，广泛应用于生物医疗、便携式电子产品、轨道交通、军事与航空航天等领域[1-3]。目前，大多数无线传感器是利用化学电池供能，但是化学电池供能的弊端日益显现，如需定期更换电池、环境污染、维护成本高等[4-5]。因此，急需找到一种绿色环保且长期稳定的新型供能方式。振动能量收集是解决无线传感器等低功耗电子产品供能问题的一种有效方案，压电式振动能量收集技术凭借功率密度大、无需额外电源、易于加工和集成等特点[6-7]受到国内外学者的广泛关注。传统悬臂梁式压电俘能器的工作频带被限制在共振频率附近非常窄的带宽内，一旦激励频率稍微偏离共振频率，输出功率会显著降低，无法满足实际应用需求[8]。为拓宽压电俘能器的工作频带，提高俘能器在低频宽带振动环境下的俘能效率，研究人员分别提出频率调谐[9]、非线性[10-12]、多模态[13-14]和升频转换[15-16]等方法。其中，非线性方法包括磁力非线性[17-18]和结构非线性[19-20]。磁力非线性以悬臂梁结构为代表，通过在悬臂梁自由端施加不同的磁力使系统表现出硬化、软化和多稳态响应。结构非线性以异形梁和屈曲梁为代表，一般通过调整梁的结构、形状和夹持方式获得非线性力，进而改善系统性能。M形屈曲梁压电俘能器（M-shaped buckled beam energy harvester，MEH）是通过对M形梁施加轴向预应力得到的一种双稳态结构[21-22]，可以实现低频率范围内的宽带能量收集。本文在屈曲式MEH的基础上引入了非线性磁力，将结构非线性与磁力非线性相结合，提出了一种磁耦合型MEH，以期进一步拓宽系统的工作频带，降低系统的跨阱阈值。

1 压电俘能器结构设计

图1的MEH结构，对M形梁施加轴向预应力使其屈曲，产生两个稳定的平衡位置A和B[21]。本文在MEH结构的基础上，通过附加外部磁铁引入了非线性磁力；图2的磁耦合型MEH结构由M形屈曲梁、磁铁和压电陶瓷（PZT-5H）组成。M形屈曲梁两端固定在基座上，PZT-5H粘贴在M形屈曲梁的固定端，磁铁C固定在屈曲梁的中间位置，磁铁D固定在屈曲梁下侧的基座上，磁铁C和D互相排斥，稳态位置B与磁铁D的间距为d。在外界激励的作用下M形屈曲梁振动，使压电片发生形变，从而将环境振动产生的机械能通过压电效应转化为电能。

2 理论模型

磁耦合型MEH为一个具有结构非线性和磁力非线性的单自由度系统（图3），包括等效非线性恢复力Fr、粘性阻尼和机电耦合项，其中等效非线性恢复力Fr由非线性磁力Fmag和M形屈曲梁的弹性恢复力Fk组成。

根据牛顿第二定律和基尔霍夫定律，磁耦合型MEH机电控制方程为

mz¨（t）+cz·（t）+Fr－θv（t）=－my¨（t）CPv·（t）+v（t）/R+θz·（t）=0（1）

其中，m为MEH的等效质量，c为等效粘性阻尼，θ为等效机电耦合系数，CP为压电元件的等效电容，R为等效负载电阻，v（t）为MEH的输出电压，x（t）为M形屈曲梁在惯性坐标系中的绝对位移，y（t）为基座在惯性坐标系中的绝对位移，z（t）为M形屈曲梁相对于基座的位移，即z（t）=x（t）- y（t），文中变量均采用国际单位。考虑到质量块的质量远大于M形屈曲梁的分布质量，因此集总参数模型中没有应用修正系数。

磁耦合型MEH等效非线性恢复力Fr为

Fr=Fk+Fmag（2）

对于磁耦合型MEH，当移除外部固定磁铁D时非线性磁力项Fmag=0，此时式（1）也表示无磁力耦合时MEH的机电控制方程。

3 实验装置和参数辨识

3.1 搭建实验平台

图4中M形梁采用316不锈钢经激光切割、折弯制成，通过调整基座的夹持角度和夹持距离来施加轴向预应力，使M形梁成为屈曲双稳态结构。实验样机安装在与振动器（HEV-200）相连接的光学平台上，振动器由功率放大器（HEA-2000C）驱动，加速度由振动控制器（ECON VT-9008）控制，加速度计（DYTRAN 3097A2）固定在光学平台上并与振动控制器连接，实现加速度闭环反馈和参数调节。示波器用于实时显示电压信号波形，数据采集卡（NI USB-6361）用于采集和记录压电元件产生的电压。

3.2 参数辨识

为了探究非线性磁力对MEH能量收集性能的影响，在M梁上引入一组磁铁（材料：钕铁硼，尺寸：10 mm×5 mm），选取间距d=40 mm的磁耦合M形屈曲梁结构与无磁铁配置（d=∞）的M形屈曲梁结构进行对比实验。为了精确捕捉系统的动态特性，使用分辨率为0.001 N的电子测力计（HANDPI HP-10）测量了两种不同配置的M形屈曲梁的等效非线性恢复力，并利用MATLAB拟合为多项式

Fr=k0+k1z（t）+k2z2（t）+k3z3（t）+…+knzn（t）（3）

其中，k0，k1，k2，…，kn表示高阶多项式的系数。

无磁耦合时M形屈曲梁的等效非线性恢复力Fr为

Fr=2.1×108·z5（t）+1.6×106·z4（t）+6.9×104·z3（t）－364.6·z2（t）－8.5·z（t）（4）

磁耦合型M形屈曲梁（d=40 mm）的等效非线性恢复力Fr为

Fr=2.3×108·z5（t）－5.83×105·z4（t）+7.13×104·z3（t）－571.3·z2（t）－2.821·z（t）（5）

图5和图6分别显示了无磁耦合时M形屈曲梁和磁耦合型M形屈曲梁的非线性恢复力与势能。图5中，由于M形梁的非对称结构特性，M形屈曲梁具有不对称的双稳态势阱，稳态位置A处的势阱深度为1.4×10-4 J，稳态位置B处的势阱深度为3.1×10-4 J。图6中，当引入非线性磁斥力后，稳态位置A处的势阱深度为0.1×10-4 J，稳态位置B处势阱深度为1.2×10-4 J，磁耦合系统的阱间势垒显著降低。

实验测量和计算了压电俘能器的等效电容、粘性阻尼、机电耦合系数等参数。其中，粘性阻尼是M形梁在自由振动状态下通过对数衰减法获得的，压电元件的电容直接测量得到。对数衰减法应在施加激励后较长后时间使用，事实上，在响应开始的阶段，非线性耗散力对阻尼的贡献远大于响应幅值较小的后期阶段。MEH的仿真参数为：θ=3.45×10-5 N/V，R=1×106 Ω，CP=22.27 nF，c=0.135 Ns/m。

4 结果与讨论

数值仿真时采用Runge-Kutta方法（MATLAB中的ode45函数），为探究不同磁铁配置的俘能器在扫频激励下的动态行为，设置激励信号为线性正弦上扫频信号，激励频率范围为（0～20） Hz。实验中激励信号的频率范围为（5～20） Hz，受到激振器工作频率（5～2 000） Hz的限制。

4.1 MEH扫频结果分析

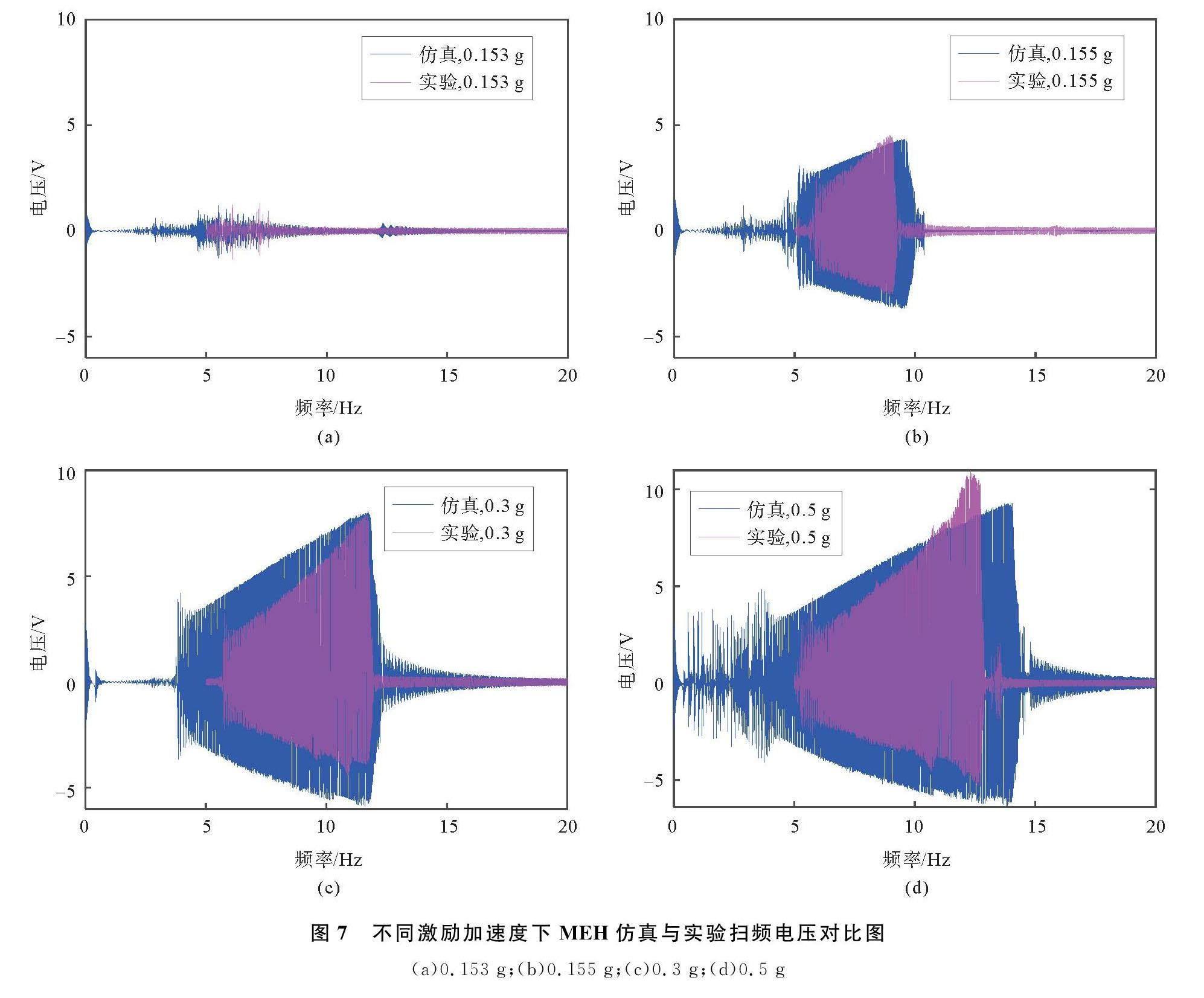
MEH在不同激励加速度下的仿真与实验结果见图7。在0.153 g加速度激励下，MEH难以跨越势垒，在（5～7） Hz频率范围内经历了短暂的阱内振荡便停止运动。在0.155 g加速度激励下，系统跨越势垒进行大振幅周期振荡，此时输出电压与工作带宽显著提升，工作带宽为3.5 Hz（6 Hz～9.5 Hz），由于M形梁的非对称结构，输出电压表现出非对称现象，单侧峰值电压为4.5 V。继续增大激励加速度，M形梁的振幅增大，系统的非对称现象更加明显。当加速度为0.3 g时，系统带宽为6.3 Hz，单侧峰值电压为7.85 V。当加速度为0.5 g时，系统带宽增加到7.4 Hz（5.3 Hz～12.7 Hz），单侧峰值电压增加到10 V，MEH在足够的激励强度下具有较高的能量收集性能。可见，仿真与实验输出压电的结果基本一致，但是在峰值电压和响应频率上略有不同，仿真中MEH在5 Hz以下的频率范围内也产生了电压输出。

4.2 磁耦合型MEH扫频结果分析

磁耦合型MEH在不同激励加速度下的仿真与实验结果见图8。在0.1 g加速度激励下，系统进行阱内运动，难以产生较大的输出电压；在0.15 g加速度激励下，磁耦合型MEH可以跨越势垒进行阱间高能振荡，此时系统的工作带宽为5 Hz（5.2 Hz～10.2 Hz），单侧峰值电压为4.35 V。这与无磁力作用的MEH类似，磁耦合型MEH的输出电压也具有非对称现象。当加速度激励增加到0.3 g时，磁耦合型MEH的工作带宽达到了7.1 Hz（5.5 Hz～12.6 Hz），单侧峰值电压为7.3 V；当加速度激励为0.5 g时，系统的工作带宽为8.3 Hz（5.5 Hz～13.8 Hz），单侧峰值电压达到了9.5 V。可以发现，仿真结果与实验结果具有相同的变化趋势，差异在合理的范围内。

对比两种不同磁铁配置的MEH实验结果可以发现，磁耦合型MEH具有更宽的工作频带。在0.3 g和0.5 g的加速度激励下，磁耦合MEH的工作带宽分别达到了7.1 Hz和8.3 Hz，比无磁耦合时分别提高了12.7%和12.2%。磁耦合型MEH的跨阱势垒降低，在0.15 g加速度激励下可以进行双稳态阱间周期运动，更加适用于低频弱振动环境下的能量收集。可见，通过引入非线性磁力，有效的提高了MEH的能量收集效率。

5 结论

本文设计了一种磁耦合型MEH，通过在MEH基础上引入非线性磁力来实现低频弱振动环境下的高效能量收集。建立了系统的集总参数模型并推导了机电控制方程，通过仿真和实验探究了非线性磁力对系统性能的影响。非线性磁力有效的降低了系统跨阱阈值，与无磁力耦合时的MEH相比，磁耦合型MEH能够在更低的激励水平下实现双稳态高能阱间振荡，并且具有更宽的工作频带。

参考文献

[1]文晟， 张铁民， 刘旭， 等. 基于压电效应的振动能量回收装置的研究进展[J]. 机械科学与技术， 2010， 29（11）： 1515-1520.

[2]徐振龙， 单小彪， 谢涛. 宽频压电振动俘能器的研究现状综述[J]. 振动与冲击， 2018， 37（8）： 190-199.

[3]张允， 王战江， 蒋淑兰， 等. 振动能量收集技术的研究现状与展望[J]. 机械科学与技术， 2019， 38（7）： 985-1018.

[4]马天兵， 吴晓东， 邹莉君， 等. 无线传感器网络的压电能量收集技术研究[J]. 传感器与微系统， 2019， 38（6）： 59-61.

[5]陈坤铭， 丁晓亮， 沈辉. 一种磁耦合的M形非线性压电振动能量收集装置[J]. 青岛大学学报 （自然科学版）， 2022， 35（3）： 39-44.

[6]芮小博， 李一博， 曾周末. 压电悬臂梁振动能量收集器研究进展[J]. 振动与冲击， 2020， 39（17）： 112-123.

[7]YANG Z， ZHOU S， ZU J， et al. High-performance piezoelectric energy harvesters and their applications[J]. Joule， 2018， 2（4）： 642-697.

[8]张骁， 沈辉， 丁晓亮， 等. 耦合双梁的非线性压电俘能器设计及仿真研究[J]. 青岛大学学报 （自然科学版）， 2021， 34（2）： 72-77.

[9]吴义鹏， 季宏丽， 裘进浩， 等. 共振频率可调式非线性压电振动能量收集器[J]. 振动与冲击， 2017， 36（5）： 12-16.

[10] ZHOU S X， ZUO L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting[J]. Communications in Nonlinear Science and Numerical Simulation， 2018， 61： 271-284.

[11] JIA Y. Review of nonlinear vibration energy harvesting： Duffing，bistability， parametric， stochastic and others[J]. Journal of Intelligent Material Systems and Structures， 2020， 31（7）： 921-944.

[12] ZHANG B， LI H Y， ZHOU S X，et al. Modeling and analysis of a three-degree-of-freedom piezoelectric vibration energy harvester for broadening bandwidth[J]. Mechanical Systems and Signal Processing， 2022， 176： 109169.

[13] 申俊， 宋芳， 熊玉仲. 弹性支撑切断式二自由度压电能量采集器研究[J]. 压电与声光， 2021， 43（5）： 646-650.

[14] HUANG X H; ZHANG C， DAI， K R. A multi-mode broadband vibration energy harvester composed of symmetrically distributed U-shaped cantilever beams[J]. Micromachines， 2021， 12（2）： 203.

[15] 黄曼娟， 侯诚， 李云飞， 等. 基于碰撞升频的MEMS压电振动能量采集系统[J]. 固体力学学报， 2019， 40（5）： 478-487.

[16] WU Y， QIU J， JI H. A frequency up-converting harvester based on internal resonance in 2-DOF nonlinear systems[J]. Journal of Physics： Conference Series， 2016， 773： 12092.

[17] ERTURK A， INMAN D J. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling[J]. Journal of Sound and Vibration， 2011， 330（10）： 2339-2353.

[18] 周生喜， 曹军义， ERTURK A， 等. 压电磁耦合振动能量俘获系统的非线性模型研究[J]. 西安交通大学学报， 2014， 48（1）： 106-111.

[19] 张旭辉， 赖正鹏， 吴中华， 等. 新型双稳态压电振动俘能系统的理论建模与实验研究[J]. 振动工程学报， 2019， 32（1）： 87-96.

[20] LEADENHAM S， ERTURK A. Unified nonlinearelectroelastic dynamics of a bimorph piezoelectric cantilever for energy harvesting， sensing， and actuation[J]. Nonlinear Dynamics， 2015， 79（3）： 1727-1743.

[21] 丁晓亮. 非线性M形梁压电振动能量收集装置的设计与实验研究[D].青岛： 青岛大学， 2021.

[22] CHEN K， DING X， TIAN L， et al. An M-shaped buckled beam for enhancing nonlinear energy harvesting[J]. Mechanical Systems and Signal Processing， 2023， 188： 110066.

Research on Magnetically Coupled M-shaped Buckled Beam Piezoelectric Energy Harvester

LUAN Hao，TIAN Li-bin，CHEN Kun-ming，DING Xiao-liang，SHEN Hui

（College of Mechanical and Electrical Engineering， Qingdao University， Qingdao 266071， China）

Abstract：

In order to improve the energy harvesting efficiency of piezoelectric energy harvester in low frequency and weak vibration environment， a magnetic coupling M-shaped buckled beam piezoelectric energy harvester （MEH） was proposed， which was derived from the original MEH. The lumped parameter model of the system was established. The nonlinear restoring force of the M-shaped buckled beam was measured and fitted experimentally， and the influence of the nonlinear magnetic force on the system performance was investigated. The simulation and experimental results show that the magnetically coupled MEH has a wider operating frequency band， reaching 8.3 Hz （5.5 Hz-13.8 Hz） under 0.5 g acceleration excitation， which is 12.2% higher than the original MEH. The magnetically coupled MEH has a lower cross-well barrier and can achieve large amplitude periodic motion under 0.15 g acceleration excitation.

Keywords：

piezoelectric energy harvester; M-shaped buckled beam; nonlinear; bistable