无力传感器的操纵手柄自适应变阻抗控制

倪涛 张泮虹 赵泽仁

摘要：

设计了一款轻量化和紧凑型的二自由度操纵手柄，并基于该操纵手柄提出了一种无力传感器的自适应变阻抗控制策略。根据操纵员操纵力大小对阻抗参数进行相应的调整以适应操纵员不同的操纵习惯；除了保证精确的位置控制外，加入了操纵手柄末端的速度控制，增强了操纵员的操纵感受。另外，在变阻抗柔顺控制的基础上加入了操纵力估计控制策略，从而避免了由于加装力传感器的额外接线导致系统复杂度增加以及由此带来的测量噪声。证明了所提控制策略在Lyapunov意义下的稳定性，说明了控制误差是收敛的，整个闭环系统的信号响应是一致极限有界的。最后，通过仿真实验以及实际台架实验验证了上述策略的有效性和稳定性。

关键词：操纵手柄；柔顺控制；阻抗控制；自适应控制；力估计

中图分类号：TP182

DOI：10.3969/j.issn.1004132X.2024.06.009

开放科学（资源服务）标识码（OSID）：

Adaptive Variable Impedance Control for Force Sensor-less Joysticks

NI Tao1，2  ZHANG Panhong1，2   ZHAO Zeren1，2

1.School of Vehicle and Energy，Yanshan University，Qinhuangdao，Hebei，066000

2.Hebei Key Laboratory of specialized Transportation Equipment，Qinhuangdao，Hebei，066000

Abstract： A lightweight and compact two-degree-of-freedom joystick was designed herein， and an adaptive variable impedance control strategy of sensor-less was proposed based on the joysticks. Firstly， the impedance parameters were adjusted according to the control forces of the operators to adapt to the different control habits of the operators. Secondly， in addition to ensuring accurate position control， the velocity control at the end-effector of the joystick was also added to improve the operator's control experience. Then， based on the variable impedance compliance control， the teleoperation force estimation control strategies were added to avoid the increase in system complexity caused by the extra wiring of the force sensor and the corresponding measurement noises. The stability of the above control strategies was proved in the Lyapunov sense， which shows that the control errors are convergent and the responses of the whole closed-loop system are uniform ultimate boundedness（UUB）. Finally， the validity and stability of the above strategies were verified by simulation experiments and actual bench experiments.

Key words： joystick; compliant control; impedance control; adaptive control; force estimation

收稿日期：20230727

基金项目：河北省重点研发计划（21351802D）；吉林省重点研发计划（20200401130GX）

0  引言

操纵手柄是操纵员与远端环境之间进行信息交换的媒介。在操纵员与操纵手柄柔顺交互的过程中，为了给予操纵员一定的力/触觉提示，保证操纵手柄末端精确稳定的位置控制是必要的，而且位置控制对阻抗和导纳控制的实现也是至关重要的［1-2］。但是，单纯的位置控制并不能保证操纵手柄末端速度输出的稳定性，速度的变化很大程度上影响了操纵员的操纵感受，进而影响操纵员的决策水平。此外，临场感是遥操纵系统中非常关键的技术［3］。临场感包括两个方面：一是从端系统能精确跟随主端控制指令；二是从端系统的实时状态能以力/触觉/听觉/视觉等形式反馈至主端系统。临场感的实现大都需要操纵手柄末端配有力/力矩传感器［4］，以测量操纵手柄末端的人手操纵力。但是，这些传感器需要额外的接线，会增加系统负担和复杂性［5］，而且力传感器较为昂贵、惯量较大，会使手柄的有效载荷降低，另外，环境温度等因素也会对力/力矩传感器造成不同程度的影响。

在涉及机器人与环境交互的应用中，阻抗的概念发挥着越来越重要的作用［6-8］。在遥操纵系统中的主控端部分，人是作为环境与操纵手柄进行交互的，为保证操纵安全，操纵手柄需要顺应操纵员的决策进行相应的动作，此时操纵员的物理行为就可以建模为阻抗。自从HOGAN［9］于1980年提出阻抗/导纳的概念以来，这方面已陆续有了很多的研究成果［10-12］。在实际应用中，阻抗控制常与自适应控制结合在一起，以应对环境或者系统中的不确定性。文献［13］提出了一种用于人机协作装配的无力传感器自适应导纳控制策略，但是该力估计方法依赖于精确的系统动力学模型。文献［14］提出了一种用于机械手与环境交互的无力传感器自适应三阶滑膜导纳控制策略，但是该方法在实际实施中需要在检测到接触力后停止3 s后继续动作，在一定程度上影响了作业效率。上述研究都是基于恒定的阻抗/导纳模型的，受中枢神经系统对人类身体行为不断调整的启发［15］，在实际的操纵手柄控制中，根据操纵任务需求和操纵员的行为实时调节阻抗参数是提高任务执行性能和安全操纵的关键。现有文献中也有提出变阻抗自适应控制策略［16-17］，但仅考虑了阻尼参数的调整，而未涉及质量参数，这样会导致系统极点右移，影响系统的动态性能。

为了克服采用力传感器带来的弊端，目前已经有文献提出了无传感器的力估计方法，文献［8］采用了一种最为直观的方法，通过测量电流差，乘以力矩常数得到操纵力矩的大小。基于电流法测量操纵力需要扣除系统摩擦、重力矩等负载项，常常需要加入系统辨识和采集电流值滤波等步骤，也有文献表明在小电流情况下可能会出现操纵力/力矩无法估计的情况［18］。此外，也有文献基于状态反馈观察器［19］将外力作为扰动来设计状态变量，然后通过误差动力学来建立状态反馈观测器，或者是建立扰动观察器，利用逆传递函数来估计扰动转矩［20］。也有将卡尔曼滤波器用于状态或者参数估计，目前已有许多关于此方面的研究［21］。关于无传感器的力估计问题，现有的研究主要存在以下几个问题：①大都是假设测量数据在每个时刻都是准确的，即没有测量噪声；②扰动观测器中如果存在其他类型干扰，估计的扭矩与实际的扭矩会有差距；③由于遥操纵，为避免信息传递延迟，数据处理效率是很有必要的，基于卡尔曼滤波的估计运算时间较长。

实验室前期开发了一款用于直升机模拟器的二自由度操纵手柄［22-24］，该操纵手柄是采用阻抗控制进行开发的，其中的位置控制采用自适应反步法，但是该操纵手柄系统末端加装有六维力传感器，且手柄尺寸较大，两个方向存在耦合，恒定的阻抗参数难以适应操纵员不同的操纵习惯，开发成本高且由于体积大导致适合的遥操纵场景较为单一。

综合上述对现有研究现状的分析，本文的研究内容包括如下几个部分：设计了一种新型的二自由度操纵手柄；根据估计出来的操纵力大小调节阻抗模型中的阻尼和质量参数；通过变阻抗模型求得操纵手柄末端期望的位置信息，通过设计速度控制器和操纵力估计控制器，在不需要力传感器的情况下实现操纵手柄末端精确的位置控制，同时实现操纵手柄末端稳定的速度控制，增强操纵员的操纵感受，有利于提高操纵安全性，保证从端作业任务顺利稳定地执行。

1  新型二自由度操纵手柄

1.1  操纵手柄的结构设计

图1所示是本文所设计的新型二自由度操纵手柄，该手柄采用两个平行并排布置的伺服电机作为驱动单元，并分别通过空间垂直交错排列的锥齿轮进行传动，以此实现电机到手柄末端的运动和力传递。相较于液压驱动式操纵手柄［25］，本文操纵手柄更侧重轻量化、小尺寸、紧凑型设计，因其传输部件转动惯量都比较小，所以系统响应快，且该操纵手柄在两个方向上的自由度相互独立，在实际运动控制中无需考虑解耦问题。

1.2  操纵手柄运动学分析

以电机1轴为x轴，以电机2轴为y轴建立坐标系，将手柄分别向三个平面投影，如图2所示。其中，l为操纵手柄的长度，具体指的是操纵员的作用点距离其旋转中心的距离。

由上述坐标系下的几何关系可得

tan θ1=y/z

tan θ2=x/z

cos θ3=z/l（1）

由此，θ1、θ2和θ3之间的关系为

tan θ3=tan2θ1+tan2θ2

sin θ3=tan2θ1+tan2θ21+tan2θ1+tan2θ2

cos θ3=11+tan2θ1+tan2θ2（2）

令

k=1+tan2θ1+tan2θ2 （3）

则操纵手柄的运动学正解为

x=ztan θ2=lcos θ3tan θ2=l/ktan θ2

y=ztan θ1=lcos θ3tan θ1=l/ktan θ1

z=lcos θ3=l/k（4）

这样就得到了操纵手柄末端在笛卡儿坐标系下的位置（x，y，z）与关节坐标系下转角（θ1，θ2）之间的关系，同理也可得运动学反解为

θ1=arctanyl2－（x2+y2）

θ2=arctanxl2－（x2+y2）（5）

1.3  操纵手柄的动力学分析

如图1所示，操纵手柄分为伺服电机的驱动部分和动力传输的被驱动部分，操纵手柄是二自由度的，对于电机驱动端，其动力学方程为

Jmθ¨m+cmθ·m+Tmf+Tm=iKTIm（6）

其中，Jm为电机驱动端的转动惯量矩阵，因为伺服电机一般都是电机和减速器成对使用，因此这里的转动惯量为电机转子惯量和减速箱转动惯量之和，被驱动部分指的是减速箱输出轴上所带操纵手柄的机械结构负载；同理，θ¨m为电机驱动端减速器箱输出的角加速度矩阵；θ·m为角速度矩阵；cm为电机的转子阻尼矩阵；Tmf为电机驱动端的摩擦项矩阵；Tm为电机驱动端的负载转矩矩阵；i为减速箱的减速比矩阵；KT为电机的转矩常数矩阵；Im为电机的电流矩阵，转矩常数与电流的乘积是电机的扭矩，为整个操纵手柄的控制输入项。

被驱动机械部分的动力学方程可以表示为

JTθ¨T+cTθ·T+TTf=Tm+τh（7）

JT=Jx+Jxy

式中，θT为齿轮对1的角位置，与电机减速器输出轴的角位置θm是相等的；Jx为x方向上的机械部件的转动惯量；Jxy为手柄端上机械部件的转动惯量；cT为被驱动端的转动阻尼；TTf为被驱动端的摩擦项；τh为操纵手柄末端的操纵力。

基于以上分析，联立式（6）和式（7），可得整个操纵手柄的动力学方程：

Jθm+cθm+Tf=τ+τh（8）

J=Jm+JT  c=cm+cT

Tf=TTf+Tmf

τ=iKTIm

式中，J、c分别为操纵手柄伺服系统的转动惯量矩阵和阻尼矩阵。

2  无力传感器的变阻抗自适应控制策略

图3所示为本文提出的加入力估计的变阻抗自适应控制策略。首先，变阻抗控制器根据操纵力求得操纵手柄两个自由度上的期望运动信息xd、yd，并发送至自适应控制器中求得操纵力Fx、Fy，随后，经过操纵手柄力/力矩雅可比矩阵JT0得到电机驱动力矩τx、τy，输入至操纵手柄系统进行控制，同时将操纵手柄实时的运动信息θx、θy经由手柄运动学模型转换至操纵手柄末端坐标系下的运动信息x、y，并将实时的末端运动信息返回至自适应控制器中，然后将控制器估计出来的操纵力返回至变阻抗模型，

求得操纵手柄下一时刻的期望运动信息，以此实现操纵手柄与操纵员的柔顺交互闭环控制。

2.1  变阻抗模型

在基于阻抗的柔顺控制框架下，如图4所示，操纵员与操纵手柄末端的交互过程是通过一个二阶的质量弹簧阻尼系统进行建模的，即

M（x¨－x¨d）+B（x·－x·d）+K（x－xd）=Fh（9）

式中，M、B、K分别为质量、阻尼和刚度矩阵；x¨d、x·d、xd分别为期望的位置、速度以及加速度矩阵；x¨、x·、x分别为实际的位置、速度以及加速度矩阵；Fh为操纵员实时的操纵力矩阵。

由于本文所设计的新型二自由度操纵手柄在两个方向是完全解耦的，因此，以某一自由度的运动来建立速度控制器，那么式（9）可以进一步表示为

mx¨d+bx·d=fm （10）

其中，m、b、fm分别为单自由度下的质量、阻尼以及操纵力。对式（10）作拉普拉斯变化可得该阻抗控制的传递函数为

H（s）=1/bms/b+1 （11）

由式（11）可以看出，质量m会影响系统状态的稳定性，质量与阻尼的比值m/b会影响系统的极点。直观上来讲，如果质量和阻尼参数较小，那么被控机器人在相对简单自由的环境下做快速运动时需要较小的操纵力；相对地，如果质量和阻尼参数较大，那么被控机器人在复杂环境下做精确运动时需要较大的操纵力，操纵员的操纵负担也会相应变大。因此，式（10）中的阻尼系数和相应的质量系数调整策略为

b=b0－η|fhc|b0+λ|fhc|m=m0b/b0（12）

式中，b0、m0分别为阻尼和质量的设定值；η、λ为调整因子；fhc为无力传感器操纵力估计值。

本文研究的是操纵手柄与操纵员之间的柔顺控制，所用传感器为力传感器，因此需要将末端测量的操纵力转换为驱动端的角位置信号，以此来得到电机驱动端的期望位置信号，进而计算相应的驱动力矩。如图2所示，从几何关系来看，以x方向为例，手柄末端操纵力与驱动端输出轴扭矩之间的变换关系为

τhx=fhxl （13）

式中，fhx为操纵员在x方向上的操纵力。

将阻抗控制计算的期望位置转换成电机驱动端的角位置信号，具体转换关系为

θmd=xd/r（14）

式中，r为锥齿轮啮合处的半径。

2.2  操纵手柄自适应速度控制器设计

不同于单纯基于位置的阻抗控制策略，本文在保证系统稳定的前提下设计了速度控制器，以进一步改善操纵员的操纵感受，同时也实现了精确的位置控制，此外，加入了操纵力的估计策略，以代替力传感器在操纵手柄控制中的作用。

为保证系统稳定性，设计速度控制器为

τv=Jθ¨r+cθ·r+Tf－σ（θ·m－θ·r）（15）

其中，θ¨r、θ·r分别为参考加速度矩阵和速度矩阵；σ为任意正整数；τv为速度控制器的控制力矩矩阵。该速度控制器包括两个部分，一部分是操纵手柄的动力学，另一部分是参考速度误差项，速度参考误差可由下式计算得到：

ε（t）=e·（t）+κe（t）=θ·m－θ·r（16）

e（t）=θm-θmd

e·（t）=θ·m-θ·md

式中，e（t）为位置误差矩阵；e·（t）为速度误差矩阵；κ为任意正常数。

参考文献［26-27］中提出并证明的人机交互模型，操纵员力矩可以表示为

τh（t）=ατr（t）+kr（t）e（t）+br（t）e·（t）（17）

式中，α为某一正常数；τr（t）为操纵员的前馈力矩；kr（t）为操纵员与操纵装置交互过程中的刚度系数；br（t）为操纵员与操纵装置交互过程中的阻尼系数。

因此，操纵力矩的自适应估计策略设计为

τhe=－ατ^r（t）－k^r（t）e（t）－b^r（t）ε·（t）（18）

ε·（t）=θ¨m-θ¨r

其中，参数估计更新律为

τ·^r（t）=Ψτ（αε（t）－μτ^r（t））

k·^r（t）=Ψk（ε（t）ε（t）－μk^r（t））

b·^r（t）=Ψb（ε（t）e·（t）－μb^r（t））（19）

式中，τ^r、k^r、b^r分别为操纵员前馈力τr、操纵员人手力刚度项kr和阻尼项br的估计值矩阵；Ψτ、Ψk、Ψb为任意正常数矩阵；μ=ρ‖ε‖；ρ为任意正常数。

这里μ的存在可以更好地平衡控制器的稳定性，速度参考误差ε变大，那么μ会相应变小，此时操作力矩估计值会变大，也就对应更加精确的运动。

最终的控制器计算的控制力矩为

τ=τv+τhe （20）

2.3  控制器稳定性证明

定理1

在整个操纵手柄的闭环系统下，所有信号均是全局一致有界的；

定义的误差ε是收敛的。

证明：

定义Lyapunov函数

V=V1（t）+V2（t） （21）

V1（t）=12εT（t）Jε（t） （22）

V2（t）=12tr（τ～Tr（t）Ψ－Tττr（t）+k～Tr（t）Ψ－Tkkr（t）+

b～Tr（t）Ψ－Tbbr（t）） （23）

其中，τ～r=τ^r-τr，k～r=k^r-kr，b～r=b^r-br，分别表示三个自适应参数的估计误差矩阵。

首先，计算V1的导数：

V·1（t）=εT（t）Jε·（t）+12εT（t）Jε（t） （24）

由式（15）、式（17）、式（18）、式（20）整理可得

Jε·（t）+cε（t）=－σε（t）－ατ～r（t）－

k～r（t）e（t）－b～r（t）e·（t）（25）

将文献［26，28］的结论εT（t）J·ε（t）-2εT（t）cε（t）=0代入式（24），并结合式（25）整理可得

V·1（t）=－εT（t）σε（t）－αεT（t）τ～r（t）－

εT（t）k～r（t）e（t）－εT（t）b～r（t）e·（t）（26）

然后，以微分的形式计算V2的导数：

V·2（t）=V2（t）－V2（t－δ）δ=

12δtr（τ～Tr（t）Ψ－Tττ～r（t）－τ～Tr（t－δ）Ψ-Tττ～r（t－δ）+

k～Tr（t）Ψ－Tkk～r（t）－k～Tr（t－δ）Ψ－Tkk～r（t－δ）+

b～Tr（t）Ψ－Tbb～r（t）－b～Tr（t－δ）Ψ－Tbb～r（t－δ））（27）

式中，δ为时间间隔；τ～Tr（t-δ）、k～Tr（t-δ）、b～Tr（t-δ）分别为τ～Tr（t）、k～Tr（t）、b～Tr（t）延迟δ时间间隔的数值。

对式（27）中的各项进行处理，首先定义Δτ～r（t）=τ～r（t）-τ～r（t-δ）=δτ·～r（t），并将自适应更新律代入，可得

12δtr（τ～Tr（t）Ψ－Tττ～r（t）－τ～Tr（t－δ）Ψ－Tττ～r（t－δ）=

12δtr（（τ～r（t）－τ～r（t－δ））TΨ－Tτ（2τ～r（t）－τ～r（t）+

τ～r（t－δ）））=12δtr（2

（Δτ～r（t））TΨ－Tττ～r（t）－

（Δτ～r（t））TΨ－TτΔτ～r（t））=αεT（t）τ～r（t）－

tr（μτ^Tr（t）τ～r（t）+12δ（Δτ～r（t））TΨ－TτΔτ～r（t））（28）

12δtr（k～Tr（t）Ψ－Tkk～r（t）－k～Tr（t－δ）Ψ－Tkk～r（t－δ））=

εT（t）k～r（t）e（t）－tr（μk^Tr（t）k～r（t）+

12δ（Δk～r（t））TΨ－TkΔk～r（t）（29）

12δtr（b～Tr（t）Ψ－Tbb～r（t）－b～Tr（t－δ）Ψ－Tbb～r（t－δ）=

εT（t）b～r（t）e·（t）－tr（μb^Tr（t）b～r（t）+

12δ（Δb～r（t））TΨ－TbΔb～r（t））（30）

定义矩阵：Θ（t）=［τTr（t）  kTr（t）  bTr（t）］，（t）=（t）-Θ（t），ΔΘ（t）=Θ（t）-Θ（t-δ），（t）是Θ（t）的估计值，（t）是Θ（t）的估计误差，Θ（t-δ）是Θ（t）延迟了δ时间间隔的值，这里定义Δ（t）=（t）-（t-δ）=δ（t）。

然后定义另一个矩阵：Ψ-T=diag（Ψ-Tτ，IΨ-Tk，IΨ-Tb），I为对应维度的单位矩阵。将式（28）～式（30）求和可得

V·2（t）=αεT（t）τ～r（t）+εT（t）k～r（t）e（t）+

εT（t）b～r（t）e·（t）－tr（μT（t）r（t）+

12δ（Δ（t））TΨ－TΔ（t））=αεT（t）τ～r（t）+

εT（t）k～r（t）e（t）+εT（t）b～r（t）e·（t）－

tr（12δ（Δ（t））TΨ－TΔ（t）+μT（t）（t）+

μΘT（t）（t））（31）

联立式（26）和式（31）可得

V·（t）=－εT（t）σε（t）－tr（12δ（Δ（t））TΨ－TΔ（t）+

μT（t）（t）+μΘT（t）（t））=

－12δtr（（Δ（t））TΨ－TΔ（t））－tr（εT（t）σε（t）+

μT（t）（t）+μΘT（t）（t））（32）

若要保证V·（t）<0成立，那么

εT（t）σε（t）+μT（t）（t）+μΘT（t）（t）≥

－σ‖ε（t）‖2+μ‖（t）‖2－μ‖Θ（t）‖‖（t）‖≥0（33）

由于σ和μ均为正常数，因此可得

‖ε（t）‖≤μ‖Θ（t）‖‖（t）‖－μ‖（t）‖2σ=

Ω1σ=Λ1（34）

‖Θ（t）‖≥

μ‖（t）‖+（μ‖（t）‖）2-4μ（-μ‖ε（t）‖）22μ=

－Ω2+Ω22+4μΩ32μ=Λ2（35）

因此，误差ε（t）是收敛有界的，且该控制器在{（‖ε（t）‖，‖Θ（t）‖），Λ1∩Λ2}区域内是稳定的。定理1是满足的。

3  仿真和台架实验验证

3.1  仿真实验及分析

根据操纵手柄设计以及电机选型时的参数，在仿真实验中，操纵手柄系统的动力学参数选择如下：J=0.0214 kg·m2；c=0.0418 kg·m2；Tmf=0.01 N·m；Tm=0.0214 N·m。两个自由度上电机型号是一样的，而操纵手柄的结构所带来的惯量以及阻尼变化不大，因此两个自由度方向均选用一样的动力学参数进行仿真实验验证。仿真实验的交互力设计为

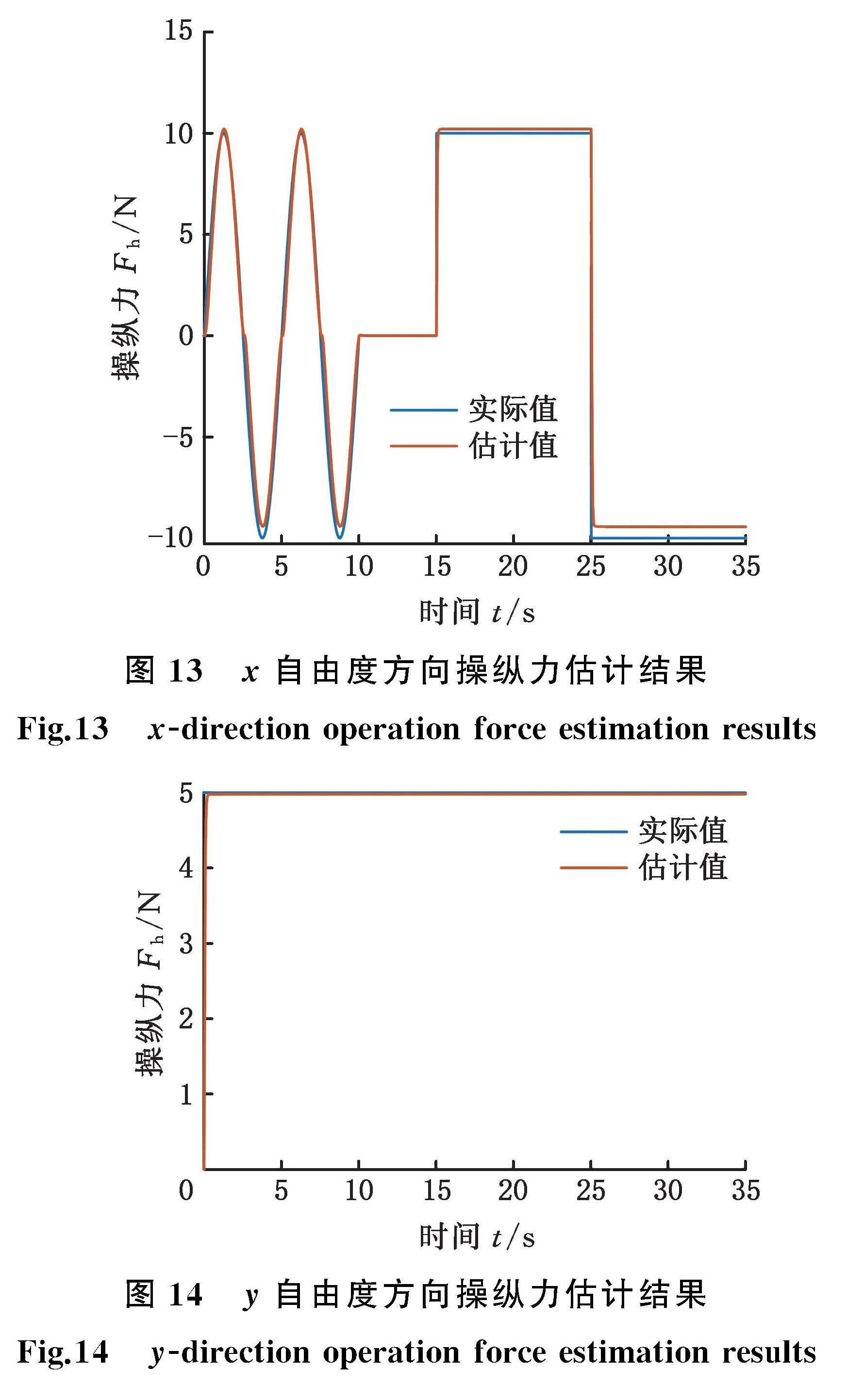
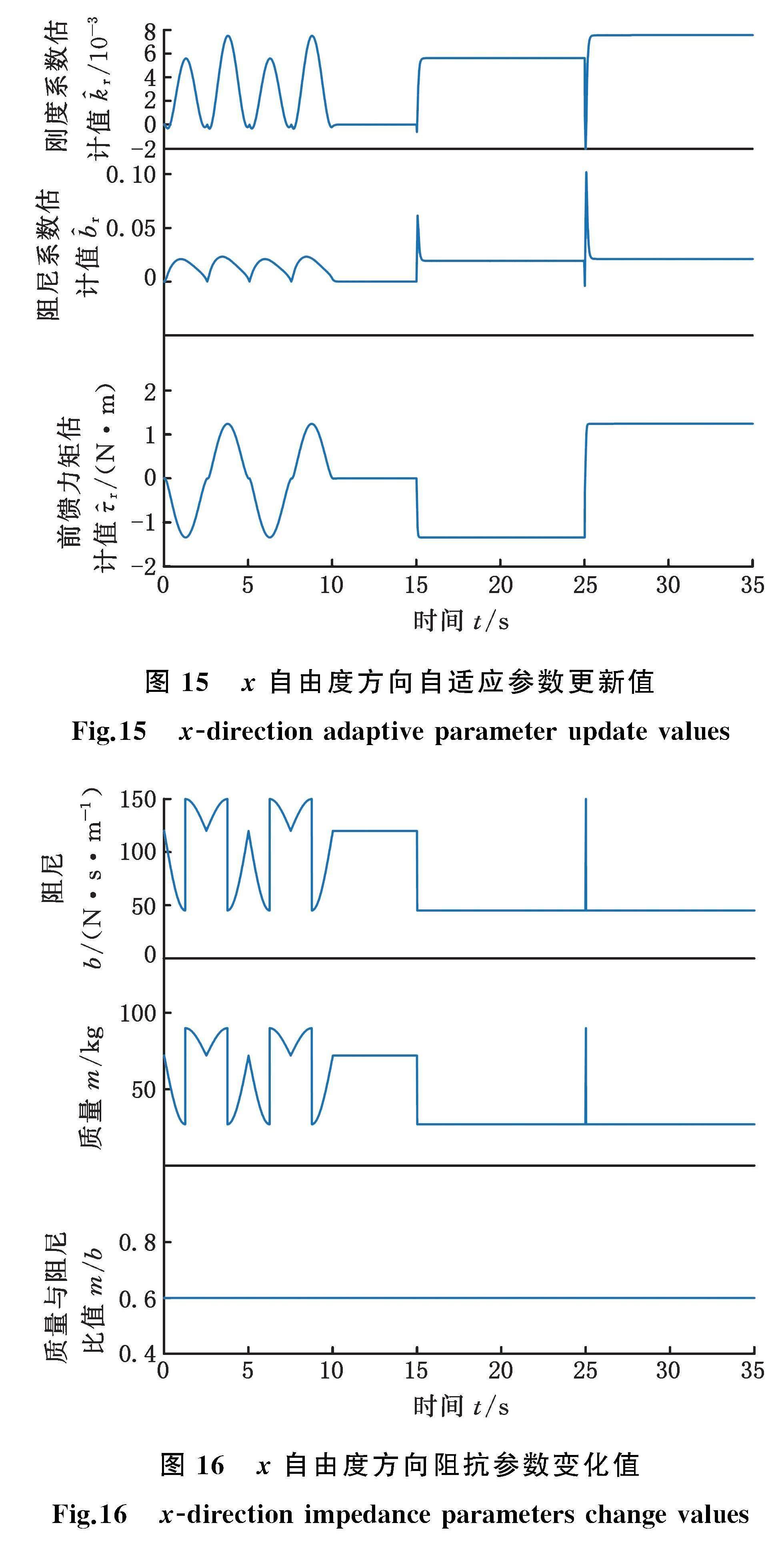
fhX=10 sin（0.4πt）N  0≤t≤10 s

0 N10 s

－10 N15 s

10 N25 s

fhY=5 N

变阻抗控制策略中的阻尼和阻抗设定值分别取b0=120 N·s/m，m0=72 kg。阻尼系数调整规则中的参数选择为η=7.5，λ=3。自适应速度控制策略中速度控制器参数σ=11，速度参考误差计算中参数κ=16，操纵力矩自适应估计策略中参数更新律参数选择为：Ψτ=5；Ψk=50；Ψb=-40；ρ=1。

图5和图6所示为x和y两个自由度上期望位置跟实际位置的跟踪效果，其中期望位置曲线是根据交互力并通过变阻抗策略求得的，从x自由度上的位置跟踪情况来看，交互力在t=15 s和t=25 s时有突变，虽然跟踪误差在一定程度上随之变大，但是并不影响位置跟踪的稳定性，且误差仍在合理范围内。同样，y自由度上仍然能实现精确的位置跟踪。

图7和图8分别为x和y自由度方向上位置跟踪的误差曲线。

图9和图10分别为x和y自由度方向上的速度变化曲线，可以看到，在没有加入操纵力矩的补偿时，操纵手柄末端的速度变化存在很多的尖点，表现为操纵员的操纵感受差，主从端的操纵透明度下降，不利于操纵手柄的稳定性操纵。对应地，加入操纵力补偿后，操纵手柄末端的速度变化曲线更为平滑，操纵员操纵更加柔顺，有利于安全作业。

图11和图12所示分别为x和y自由度方向上输出的控制力矩。

图13和图14所示分别是x和y自由度方向上的力估计结果，该力估计结果作为补偿力加入至操纵手柄的控制力矩中，操纵手柄末端的速度输出更加稳定。从x自由度方向的力估计结果可以看出，即便是在t=15 s和t=25 s发生交互力突变，力估计控制器也能稳定输出估计结果，且不会造成大误差，这将有利于操纵手柄末端的位置以及速度控制器精确稳定输出，进而增强操纵员的操纵感受。通过图13也可以看到，突变处会对操纵力的估计准确度造成一定的影响，而且突变程度变大之后操纵力的估计误差会变大，但是可以看到，虽然误差变大，但是并不影响操纵力估计的稳定性，因此不会对整个控制器的稳定性造成影响。

由于x自由度上交互力的设计较为复杂，为了在能说明问题的前提下保证论文的简洁性，接下来仅以x自由度为例说明自适应参数更新规律以及变阻抗参数的变化规律。图15所示为x自由度方向上自适应控制器中参数更新律变化，可以看到，参数的变化范围是有界的，也进一步说明了该控制器是稳定的。图16所示为x自由度方向上阻抗参数变化规律，可以看到，随着操纵手柄末端交互力的变化，阻抗模型中的系数也在调整，以实现稳定的位置和速度控制。此外，为了保证系统的极点不会随着质量和阻尼系数的变化而发生变化，在控制器设计中将m/b的比值设定为0.6。

3.2  台架实验及分析

为验证本文所提无力传感器变阻抗自适应控制器的正确性，搭建实验台架如图17所示，这里需要提到的是，为了验证本文所述力估计策略的有效性，在操纵手柄末端加装力传感器进行实验。

操纵手柄的驱动模块选用maxon的直流有刷电机加行星齿轮减速箱，减速比为190。电机末端的编码器与对应的驱动器串联，2个电机驱动器和力传感器的放大模块也串行连接，然后连接至倍福PLC上读取编码器和力传感器的数据，并将读取的数据以CAN通信的形式通过dSPACE传至上位机的控制器中。最后将控制器解算出来的控制力矩通过CAN传至倍福PLC，通过驱动器控制电机运动。将CAN信号分析仪串联进电路中是为了观测由于信号不稳造成的控制器失效问题。

这里以x自由度方向上的控制情况来说明算法有效性。实验结果与仿真结果基本保持一致，如图18所示，控制策略能实现精确的位置跟随，结合图19可以看出，位置跟踪误差控制在0.03 rad内，完全满足操纵手柄末端位置控制精度。图20所示为加入力补偿控制前后的操纵手柄末端速度曲线，其结果表明在加入力补偿控制策略后，操纵手柄末端的速度变化更加柔顺平滑。图21所示是传感器测得的操纵力大小与控制器所估计的操纵力大小的对比，可以看出，所估计结果与实际测得的数据基本吻合，进一步说明了本文所提控制器能很好地替代传感器，降低了系统的复杂度以及开发成本。

图22～图24所示为控制力矩、自适应参数变化情况以及变阻抗控制参数的变化情况，数据同样都在合理范围内，且都是全局一致有界的。

4  结论

本文设计了一种新型二自由度操纵手柄，具有轻量化、解耦控制等优点，针对该操纵手柄，提出了一种无力传感器的自适应阻抗控制器，从速度控制和操纵力估计两部分设计了控制策略。考虑到不同操纵员的操纵习惯，加入了阻抗控制参数的调整策略，除了能保证操纵手柄末端速度的稳定性外，也能实现操纵手柄末端的精确位置控制，并且可以替换力传感器得到人手操纵力，大大降低了系统复杂度和开发成本。此外，证明了该控制策略在Lyapunov意义下的稳定性。最后，通过仿真实验和台架实验，在设计的新型二自由度操纵手柄上验证了控制策略的准确性和可行性。仿真和试验结果均表明，该控制策略能有效降低操纵手柄末端速度的突变点，增强操纵员的操纵感受，位置控制最大误差在0.03 rad内，完全满足精度要求。力估计结果与传感器数据基本吻合，将该力估计结果用于期望位置计算，整个闭环系统的信号也均是全局一致有界的。但是通过仿真实验发现，在操纵力突变的时候，力估计的误差会变大，将来的研究会致力于提高操纵力估计控制器的自适应性。

参考文献：

［1］  徐冰洁. 基于末端六维力传感器的操作臂力/位混合控制及应用［D］. 济南：山东大学， 2021.

XU Bingjie. Force/Position Hybrid Control of Manipulator Based on Six-dimensional Force Sensor at the End and Its Application［D］. Jinan：Shandong University， 2021.

［2］  董晓星， 李戈， 刘刚峰，等. 冗余空间机械臂的运动学和笛卡尔阻抗控制方法［J］. 中国机械工程， 2014， 25（1）：36-41.

DONG Xiaoxing， LI Ge， LIU Gangfeng，et al. Kinematics and Cartesian Impedance Control for Redundant Space Robotic Arm［J］. China Mechanical Engineering， 2014， 25（1）：36-41.

［3］  颜晗，董跃巍，李铁军. 面向高空幕墙安装的力反馈遥操作系统研究［J］. 中国机械工程， 2017， 28（16）：1977-1986.

YAN Han，DONG Yuewei，LI Tiejun. Research on Tele-operation Systems for Installation of Aerial Curtain Walls Based on Force Feedbacks［J］. China Mechanical Engineering， 2017， 28（16）：1977-1986.

［4］  ENRIQUE S A. Force Estimation for Teleoperating Industrial Robots［M］. New York：IntechOpen， 2016.

［5］  LIU Sichao， WANG Lihui，WANG X V. Sensorless Force Estimation for Industrial Robots Using Disturbance Observer and Neural Learning of Friction Approximation［J］. Robotics and Computer-integrated Manufacturing，2021，71：102168.

［6］  朱安， 艾海平， 陈力. 基于障碍Lyapunov函数的双臂空间机器人捕获卫星柔顺控制［J］. 中国机械工程， 2022， 33（24）：2997-3006.

ZHU An， AI Haiping， CHEN Li. Compliance Control of Dual-arm Space Robot Capture Satellite Based on Barrier Lyapunov Functions［J］. China Mechanical Engineering， 2022， 33（24）：2997-3006.

［7］  刘俊， 阮小栋， 杨鹏亮， 等. 变胞机器人重构及转向时足着地柔顺性控制［J］. 中国机械工程， 2022， 33（24）：2917-2926.

LIU Jun， RUAN Xiaodong， YANG Pengliang，et al. Control of Foot Landing Flexibility in Metamorphic Robot Reconstruction and Steering［J］. China Mechanical Engineering， 2022， 33（24）：2917-2926.

［8］  倪涛， 徐海远， 李东， 等. 六自由度平台动力学前馈柔顺控制研究［J］. 中国机械工程， 2022， 33（6）：683-689.

NI Tao， XU Haiyuan， LI Dong，et al. Research on Dynamics Feedforward Compliance Control of 6-DOF Platforms［J］. China Mechanical Engineering， 2022， 33（6）：683-689.

［9］  HOGAN N. Impedance Control：an Approach to Manipulation：Part I―Theory［J］. Journal of Dynamic Systems， Measurement & Control， 1985， 107（1）：1-24.

［10］  PENG Shigang， YU Meng， CHENG Xiang， et al. Bilateral Teleoperation System with Integrated Position/Force Impedance Control for Assembly Tasks［J］. Applied Sciences， 2023， 13（4）：2568.

［11］  袁俊杰，胡佳星，张忠海，等.关节力矩反馈型协作机器人的阻抗控制研究［J］.传感器与微系统， 2023， 42（7）：32-35.

YUAN Junjie， HU Jiaxing， ZHANG Zhonghai， et al. Research on Impedance Control of Joint Torque Feedback Cooperative Robot［J］. Transducer and Microsystem Technologies，2023， 42（7）：32-35.

［12］  ZHAO Xingwei， CHEN Yiming， QIAN Lu， et al. Human-robot Collaboration Framework Based on Impedance Control in Robotic Assembly［J］. Engineering， 2023， 30：83-92.

［13］  LIU Sichao， WANG Lihui，WANG X V. Sensorless Haptic Control for Human-robot Collaborative Assembly［J］. CIRP Journal of Manufacturing Science and Technology， 2021， 32：132-144.

［14］  LE Q D， KANG H J. Sensor-less Contact Force Estimation in Physical Human-robot Interaction［J］. Lecture Notes in Computer Science， 2021， 12837：233-244.

［15］  WEI Qiang， LI Zhijun， ZHAO Kuankuan. Synergy-based Control of Assistive Lower-limb Exoskeletons by Skill Transfer［J］. IEEE/ASME Transactions on Mechatronics， 2020， 25（2）：705-715.

［16］  DONG Jianwei， XU Jianming， ZHOU Qiaoqian， et al. Physical Human-robot Interaction Force Control Method Based on Adaptive Variable Impedance［J］. Journal of the Franklin Institute， 2020， 357（12）：7864-7878.

［17］  李佳欣， 于殿勇， 谭向全， 等. 基于变阻抗的人机协作避障技术研究［J］. 组合机床与自动加工技术， 2023（5）：134-137.

LI Jiaxin， YU Dianyong， TAN Xiangquan， et al. Research on Human-robot Cooperative Obstacle Avoidance Technology Based on Variable Impedance［J］. Modular Machine Tool & Automatic Manufacturing Technique， 2023（5）：134-137.

［18］  KUNEGUCHI T， NODA Y， SAGO Y， et al. Operational Assistance System Using 3-DOF Joystick with Reaction Force Display to Load Transfer Machine in a Plane［C］∥11th International Conference on Informatics in Control， Automation and Robotics. Vienna， 2014：346-352.

［19］  BUJA G S，MENIS R，VALLA M I. Disturbance Torque Estimation in a Sensorless DC Drive［J］. IEEE Transactions on Industrial Electronics，1995，42（4）：351-357.

［20］  LIU C S，PENG H. Disturbance Observer Based Tracking Control［J］. Journal of Dynamic Systems， Measurement， and Control， 2000，122（2）：332-335.

［21］  LEE S C， AHN H S. Sensorless Torque Estimation Using Adaptive Kalman Filter and Disturbance Estimator［C］∥IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications. Kochi， 2010：87-92.

［22］  赵苗苗. 直升机模拟器的电驱动操纵负荷系统研究［D］. 长春：吉林大学， 2017.

ZHAO Miaomiao. Research on Electric Drive Control Loading System of Helicopter Simulator［D］. Changchun：Jilin University， 2017.

［23］  张渐尧. 直升机模拟器的操纵力感控制系统研究［D］. 秦皇岛：燕山大学， 2020.

ZHANG Jianyao. Research on Force-feel Control System on Helicopter Simulator［D］. Qinhuangdao：Yanshan University， 2020.

［24］  ZHAO Dingxuan， ZHANG Jianyao， CARBONE G， et al. Dynamic Parameters Identification of a Haptic Interface for a Helicopter Flight Simulator［J］. Mechanical Science， 2020， 11（1）：193-204.

［25］  BACHMAN P， MILECKI A. Investigation of Electrohydraulic Drive Control System with the Haptic Joystick［J］. Acta Mechanica et Automatica， 2018， 12（1）：5-10.

［26］  LIU Xia， WU Jianguo， WANG Lu. Sensorless Variable Impedance Compliant Control for Human-robot Interaction［J］. AIP Advances 2022， 12：115121.

［27］  SHARIFI M， AZIMI V， MUSHAHWAR V K， et al. Impedance Learning-based Adaptive Control for Human-robot Interaction［J］. IEEE Transactions on Control Systems Technology， 2022， 30（4）：1345-1358.

［28］  TING Zou， ANGELES J， HASSANI F. Dynamic Modelling and Trajectory Tracking Control of Unmanned Tracked Vehicles［J］. Robotics & Autonomous Systems， 2018， 110：102-111.

（编辑  袁兴玲）

作者简介：

倪  涛，男，1978年生，教授。研究方向为工程机械遥操纵。E-mail：nitao@ysu.edu.cn。

张泮虹（通信作者），女，1993年生，博士研究生。研究方向为触觉遥操纵手柄开发。E-mail：zph@stumail.ysu.edu.cn。