电磁感应的常考题型解析

王凯

摘 要：感应电流是联系力和电的桥梁.文章对电磁感应相关知识点进行梳理，对常考题型进行归纳解析，以期提升学生物理学科核心素养.

关键词：电磁感应；感应电流；磁通量；感应电动势；安培力

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）15-0088-03

感应电流将电学与力学融合在一起，试题的难度也会有所提升.下面对电磁感应中的常考题型进行分类解析.

1 判断磁通量的大小

例1 图1所示是两个同心放置的共面金属圆环a和b，一条形磁铁穿过圆环的圆心且与环面垂直，则穿过两环的磁通量的大小关系为 （   ）.

A.Φa>Φb B.Φa<Φb

C.Φa=Φb D.无法比较

分析 在闭合线圈中包含磁体（包括通电螺线管）时，线圈中存在相反的磁场，在这种情况下，一般要分区域定性分析或定量计算各自的磁通量，然后再求它们的代数和.

例1中，磁铁内部的磁感线是磁铁外部的总和，但由于方向相反，线圈中的磁通量是这两者的差值.因此，线圈的面积越大，线圈中的磁通量反而越小.题目中穿过线圈的磁感线的方向相反，计算磁通量时，可以用正、负对它们加以区别，但这里的正、负绝非描述矢量的正、负号的含义.

解析 线圈把磁铁包围在其中，磁铁的内部和外部磁感线的方向是相反的，计算磁通量时要注意正、负问题.

磁感线是闭合曲线，在条形磁铁外部从N极到S极，在内部从S极到N极，线圈中的磁通量应是这两部分磁通量的代数和.磁铁外部空间的所有磁感线都要穿过内部，又因为圆环a的面积小于圆环b的面积，故从外部N极到S极穿过a面的磁感线条数少，则穿过a面的磁通量大，选项A正确.

点评 关于条形磁铁的磁感线，教科书中展现在我们面前的几乎都是磁铁外部的磁感线的分布，从而使很多同学忽视了磁铁内部的磁感线，并且内部的磁感线是磁铁外部的总和，是主要的，只讨论外部的磁感线是主次不分.

2 确定感应电流的方向

例2 如图2所示，闭合导体环M固定，条形磁铁S极向下以初速度v0沿过导体环圆心的竖直线下落，在此过程中导体环中的感应电流方向如何？

分析 楞次定律在本质上与能量守恒定律是一致的，它所涉及的过程是能量转化，依据能量守恒，再结合楞次定律中的“阻碍”特点，楞次定律在具体的应用中还可衍化出许多实用的方法.以本题为例，导体环M中的感应电流是由于磁铁与导体环的相对运动产生的，那么导体环M中的感应电流产生的磁场将会阻碍磁铁的相对运动.所以，当磁铁靠近导体环时，导体环中的感应电流将阻碍其靠近；当磁铁远离导体环时，导体环中的感应电流又将阻碍其远离导体环.在这里对磁铁的阻碍是通过导体环中的电流产生的磁场对磁铁的作用力实现的，此时只需将导体环（环形电流） 看成一个小磁体，这一磁体与磁铁的相互作用便是对磁铁与导体环相互运动的阻碍，由此可知导体环的 N、S 极，进而容易确定导体环中的电流方向.

解析 从感应电流的磁通总是“阻碍磁通量变化”来看，当条形磁铁的中心恰好位于导体环M所在的平面时，磁铁内部向上的磁感线都穿过了导体环，而磁铁外部向下穿过导体环的磁通量最少，所以此时穿过导体环M的磁通量最大.因此全过程中原磁场方向向上，先增后减，感应电流的磁场方向先下后上，感应电流先顺时针后逆时针（俯视）.

点评 在运用楞次定律时，一定要注意“阻碍”不等于“反向”，“阻碍”不是“阻止”.而且，在实际应用过程中应从多方面来理解“阻碍”的含义，如在由相对运动引起磁通量变化的情况中，阻碍表现在相互的作用力上，即“来拒去留”；如果磁通量的变化是由磁场强弱的变化引起的，阻碍体现在感应磁场的方向上则是“增反减同”.此外，“阻碍”还可以表现在导体环的面积变化趋势或运动趋势上，等等.

3 闭合电路中的切割磁感线运动

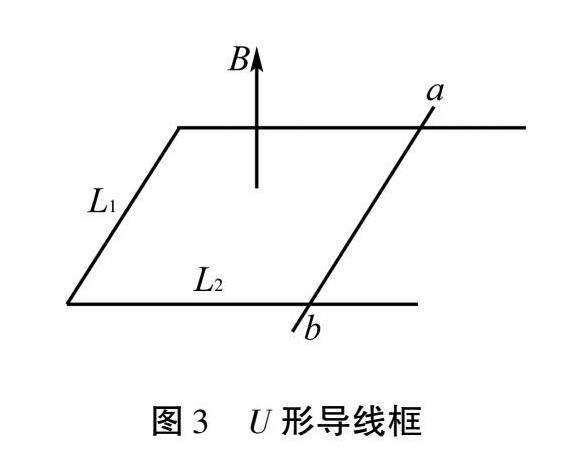
例3[1] 如图3所示，U形导线框固定在水平面上，右端放有质量为m的金属棒ab，ab与导轨间的动摩擦因数为μ，它们围成的矩形边长分别为L1、L2，回路的总电阻为R.从t=0时刻起，在竖直向上方向加一个随时间均匀变化的匀强磁场B=kt（k>0），那么在t为多大时，金属棒开始移动？

分析 在ab未移动前，应有E=nΔBΔt·S=kL1L2，回路中将会存在恒定的电流，但由于磁场强度的变化，ab受到的安培力将会发生变化，而B=kt，则经过一定的时间后，安培力定会大于摩擦力，从而导致金属棒开始运动.

解析 由E=ΔΦΔt=kL1L2可知，回路中感应电动势是恒定的，电流大小也是恒定的，但由于安培力F=BIL∝B=kt∝t，随时间的增大，安培力将随之增大.当安培力增大到等于最大静摩擦力时，ab将开始向左移动，这时有

kt·L1·kL1L2R=μmg.

所以，当t=μmgRk2L21L2时，金属棒开始移动.

点评 当闭合回路中的磁通量发生变化时，回路中将产生感应电动势，根据不同的情况，电动势的公式E=nΔΦΔt有三种不同的表达形式：

（1）如果B不变、S变化，则E=nΔSΔt·B.

（2）如果S不变、B变化，则E=nΔBΔt·S.

（3）如果B和S同时改变，则E=nΔ（BS）Δt.

例4[2] 如图4所示，把金属线框从匀强磁场中匀速拉出，是快拉做功多还是慢拉做功多？

分析 金属框穿越有界磁场的问题极为常见，无非是涉及这一过程的外力、安培力、做功、功率、流过导体的电量，以及金属框某一部分产生的电动势或某部分两端的电势差之类的问题，实质上是力学问题或电路问题在磁场中的具体应用，其基础性非常强.对于本题，给出下面三种解法，望能从中体会其基本方法的运用.

解析 线框cd边出磁场后，线框产生感应电动势、感应电流，并受安培力，线框做匀速运动，则外力F=F安.

解法1 因为线框做匀速运动，所以

F=F 安=BIL=BBLvRL，

拉力所做的功为W=Fd=B2L2dvR.

无论快拉、慢拉，磁感应强度B、ab边长L、拉出的位移d、线框电阻R都相同，所以拉出速度v越大，做功越多.

解法2 思路基本与解法1相同，只是线框产生的感应电动势用法拉第电磁感应定律表达，即E=ΔΦΔt，于是有

W=Fd=BΔΦΔtRLd=BLdΔΦR·1Δt.

无论快拉、慢拉，线框拉出过程的磁通量变化ΔΦ都相同，所用时间越短，做功越多，即快拉做功多.

解法3 从能的转化和守恒定律看，外力拉线框所做的功全部转化为线框所产生的电能 （这一电能又通过线框电阻R变成焦耳热），则

W=E2△tR=△Φ2R△t.

由上式可知，△t越小做功越多，所以快拉做功多.

点评 解法3不受线框所处的磁场是不是匀强磁场的限制，也不要求一定匀速拉出.所以，这个解法具有较为普遍适用的意义.我们知道，有安培力参与的运动，或是匀速运动，或是变加速运动，或是匀变速运动.因此，描述这样的运动过程，往往只能采用能的转化和守恒定律.

例5 如图5所示，用一根均匀导线做成的矩形导线框abcd放在匀强磁场中，线框平面与磁场方向垂直，ad、bc边上跨放着均匀直导线ef，各导线的电阻不可忽略.当将导线ef从ab附近匀速向右移动到cd附近的过程中（  ）.

A.ef受到的磁场力方向向右

B.ef两端的电压始终不变

C.ef中的电流先变小后变大

D.ef中的电流先变大后变小

分析 在该模型中，由于只有ef在切割磁感线，故它在整个电路中充当电源，并且其电阻为电源的内阻，其他部分外电路的电阻为导线的电阻值，于是可将框架结构转换为电路，如图6所示.在ef匀速向右移动的过程中，ef左右两侧的电阻都在改变，但其总值并没有改变，由并联电路的知识可知，当ef运动到中间位置时，电路中的总电阻最大，通过ef的电流最小，这一问题体现了电路的动态分析特征.

至于ef所受到的安培力，不论是从阻碍的特征出发，还是直接从感应电流的方向用左手定则，都可确定其方向是向左的.

解析 ef导线切割磁感线产生感应电动势相当于电源，等效电路如图6所示，在ef中电流先减小后增大.答案C正确.

4 结束语

定量分析问题，大多仅涉及闭合电路一部分导体做切割磁感线运动且匀速运动的问题.物理过程是： 闭合电路一部分导体做切割磁感线运动，产生感应电动势E=BLv.在纯电阻电路中，由全电路欧姆定律可知产生的感应电流I=ER=BLvR，从而使运动导体受到安培力F=BIL，为了维持匀速运动，必须满足∑F=0.

参考文献：

［1］徐华兵.剖析电磁感应中的电容器问题[J].高中数理化，2018（23）：36-38.

[2] 麦祖发.力学知识在解答电磁感应问题中的运用[J].数理天地（高中版），2023（20）：20-21.

［责任编辑：李 璟］