典型峡谷Ⅴ型地貌下桥址区风特性
2024-06-28张玥刘子琦石慧慧
张玥 刘子琦 石慧慧

摘 要:为得到山区峡谷典型Ⅴ型地形下的桥梁抗风设计的关键风特性参数,通过“数值风洞试验”建立模型,以实桥为工程背景构建三维地形网格,基于3种典型湍流模型和流体壁面粗糙度对桥位的风场特性进行分析,选取最优湍流模型和流体壁面粗糙度对该地形桥位处的风场特性进行分析;围绕两个影响桥址区风特性的地形参数(山体高度和夹角),阐明Ⅴ型峡谷地形下风特性参数的变化规律,并与现行规范进行对比,推算桥面设计基准风速。结果表明:该Ⅴ型峡谷地形的最佳湍流模型和流体壁面粗糙度分别为RNG k-ε和20 m;随着山体高度及山体夹角两参数的变化,风速增加幅度分别为2.37%~12.56%和1.24%~6.98%;山体高度及山体夹角两变参数下,梯度风高度分别为700 m和800 m左右;实际湍流强度大于规范中四类地表规范值,在离地高度40 m范围内,湍流强度更接近于D类地表。实际Ⅴ型峡谷桥址区不能简单按规范归为C类或D类地形,在设计风参数计算时应综合考虑规范和经验公式,还可借助模拟手段来提高其准确性。
关键词:风特性;Ⅴ型峡谷;数值风洞试验;湍流模型;地形参数;设计基准风速
中图分类号:U 442
文献标志码:A
文章编号:1672-9315(2024)03-0575-12
DOI:10.13800/j.cnki.xakjdxxb.2024.0317开放科学(资源服务)标识码(OSID):
Wind characteristics of bridge site under typical canyon
V-shaped landform
ZHANG Yue,LIU Ziqi,SHI Huihui
(College of Architecture and Civil Engineering,Xian University of Science and Technology,Xian 710054,China)
Abstract:In order to obtain the key wind characteristic parameters for wind resistance design of Bridges in typical V-shaped terrain in mountain canyons,an model was established by the method of “numerical wind tunnel test”,a three-dimensional terrain grid was constructed with real bridges as the engineering object,and the wind field characteristics of bridge sites were analyzed based on three typical turbulence models and fluid wall roughness.The optimal turbulence model and fluid wall roughness were selected to explore the wind field characteristics at the bridge site.From these two topographic parameters,mountain height and angle,which affect the wind characteristics of the bridge site,the variation law of the downwind characteristic parameters of the V-shaped canyon terrain is summarized,and the design reference wind speed of the bridge deck is calculated by comparing with the current norms.The results show that the optimal turbulence model and fluid wall roughness of the V-shaped canyon terrain are RNG and 20m respectively.With the change of mountain height and mountain angle,the increase of wind speed is 2.37%~12.56% and 1.24%~6.98%,respectively.Under the two variable parameters of mountain height and mountain angle,the gradient wind height is about 700 m and 800 m respectively.The actual turbulence intensity is greater than the standard values of the four types of surface in the specification,and the turbulence intensity is closer to the D type surface in the range of 40 m above the ground.The actual V-shaped canyon bridge site can not be classified as C or D terrain
simply according to the code.The code and empirical formula must be considered comprehensively when designing the wind parameter calculation,and the accuracy could be improved by means of simulation.
Key words:wind characteristics;V-shaped canyon;numerical wind tunnel test;turbulence model;terrain parameters;basic design wind speed
0 引 言
随着经济和科技的快速发展,在西部山区建造的桥梁日益增多,当风遇到障碍物山体和峡谷时,会出现峡谷风的放大效应和山体绕流、附着效应,尤其在复杂山区地形,山体对桥址区的风场分布规律和流场作用机理的影响极大。为了保证桥梁的正常运营和后期维护,需探究山区典型地形桥址区风场特性的分布规律和典型风向角影响下的分布机理[1-3]。
目前,由于现行抗风规范中对地表的分类较粗略,并未详细划分典型的山区峡谷类型而是统一归为D类,导致在具体的典型峡谷地貌中,规范确定值与数值风洞模拟所得结果产生差异。周继等以湘江特大桥为例研究复杂地形桥位下的风特性,发现经过CFD数值模拟分析的主梁设计基准风速与抗风规范确定的基准风速相比偏大[4]。所以对于山区复杂地形尤其是横跨两山峡谷地貌下的桥梁结构,其抗风设计所需风荷载,仍需借助物理风洞试验和现场实测等方法进行相关风参数的修正。针对上述问题,当风洞试验或现场实测的数据支撑难以得到时,数值模拟快速准确地确定设计所需风特性参数的优势就体现出来了。借助“数值风洞”保证抗风设计的准确性和可靠性就成了这一方法的关键,一般来说计算域中湍流模型的选取很大程度会导致计算结果的准确性。目前针对湍流模型的研究很多,
张向旭、李永乐、于舰涵等选取SST k-ε模型对复杂山体地形进行风场模拟计算分析[5-7];薛亚飞、孙亭亭、王铁强等采用了RNG k-ε模型对山区桥位处风场进行了模拟研究[8-10]。其中,王铁强基于6种湍流模型进行了分析,得出Standard k-ω模型和SST k-ω模型用于高雷诺数流场的近地面风场计算时会出现较大的误差;而RNG k-ε模型和Realizable k-ε、RSM模型的模拟结果在总体误差比较相近且均较小;Realizable k-ε模型在主要计算旋转和静态流动区域时不能提供自然的湍流黏度;RSM用于复杂流动时有潜力达到更高的精度,但计算量大。最终可知RNG k-ε模型较适合在风场模拟中使用[10];于涛,唐昂等[11-18]采用了Realizable k-ε模型对山区风场进行了模拟运算,其中,冯林以黄贤村山体风场为研究对象,选取了3种典型湍流模型与实测数据比较,得出RNG k-ε模型结果误差最大,平均误差约达5%,而Realizable k-ε模型的结果误差最小,误差值约为3%,Realizable k-ε模型模拟精度较高;在地形参数方面,楼文娟、陈平、李正昊等通过数值模拟和风洞试验较全面的研究了山体之间的间距、山体形状以及峡谷长度等地形参数对峡谷内部风场的影响[19-21];BOWEN、CAO、LUBITZ等分别研究了山体坡度、形状和来流风向角等流场影响因素对山地风场的影响[22-24]。
针对峡谷地形参数对风场影响的研究多以理想二维模型或由单峰山丘轮廓模型组成的三维模型为研究对象,二维模型无法全面地考虑实际山体情况,而单峰山丘组成的三维模型无法在其基础上改变山体高度和山体夹角来进行研究。基于此,以典型Ⅴ型峡谷实际地形为研究对象,以矮寨大桥为工程背景,对山体地形参数改变时的风场变化规律进行分析,并提出梯度风高度范围和计算出该峡谷地形下桥址区的基准风速,以及这种地形下适应的地表规范归属类型,为后续相似地形模型的建立及抗风参数的研究提供参考。
1 Ⅴ型谷三维地形模型
1.1 实际地形模型
矮寨大桥位于湖南湘西州吉首市矮寨镇,海拔高度680~900 m,跨中桥面标高与谷底高差达340 m。根据三维数字地形图LSV与下载软件定位矮寨大桥并选取计算域,桥位坐标(N28°19′58.48″,E109°35′53.75″)。考虑到地形边界对风场回流的影响和保证流场的充分发展,以及为了更接近真实的风场,确定将计算域选为2 200 m×2 200 m×2 000 m,通过提取该地形高程数据点,将高程点换算为经纬度坐标后,利用万能坐标转换器转换为直角坐标系即XYZ形式,导入Rhinoceros生成三维地形曲面,再通过Fluent前处理软件Gambit对犀牛软件Rhinoceros导出的sat文件进行建模,利用Gambit生成计算模型。矮寨大桥的桥位地形如图1所示,由犀牛软件Rhinoceros生成的地形曲面如图2所示。
1.2 网格划分以及边界条件划分
运用Gambit进行非结构性网格划分、设定边界条件,采用三角形非结构化网格,近地面最小网格尺度30 mm。速度入口边界参数时一般采用均匀流或将风速设置成风速剖面计算,以此模拟实际峡谷地形中风速沿高度变化而变化的特性,试验模拟采用均匀流。数值模拟计算仅针对最不利均匀流场进行分析,由唐金旺针对地形做的风洞试验[14]可知均匀流场的最不利风速为10 m/s,故入口风速值设置为10 m/s。其中,针对计算域边界条件和网格划分如图3~图5所示。
1.3 湍流模型及计算工况
为了确保此类地形风场特性计算的准确性,选取两方程带旋修正Realizable k-ε、重整化群RNG k-ε和剪应力传输SST k-ε 3种湍流模型进行对比分析,湍流模型求解过程中的各项具体参数设置见表1。童祎巍对矮寨大桥安装设置观测点进行现场实测[25],由实测所统计得出的强风样本可知矮寨大桥所处峡谷的大风大都来自偏北风,其次是偏西方向和偏东方向。考虑矮寨大桥实测强风风向及桥址处峡谷两侧山体对风的遮挡效应,按照标准逆时针设置以下3种典型风向角作为计算工况进行数值模拟研究:风向角为0°时,
记为工况1,风向角为90°时记为工况2,风向角
为270°时记为工况3,3种工况均采用图4中设定的计算域边界条件。为了分析桥位处风速和湍流强度沿高程的变化,拟选取矮寨大桥上的5个特定位置作为测点研究其竖方向上的风速和湍流强度大小。测点0~4分别对应跨中点、吉首岸桥跨四分点、吉首岸桥塔位置、茶洞岸跨四分点、茶洞岸桥塔位置。3种工况的风向角与测点布置如图6、图7所示。
2 实际桥址区的风特性分析
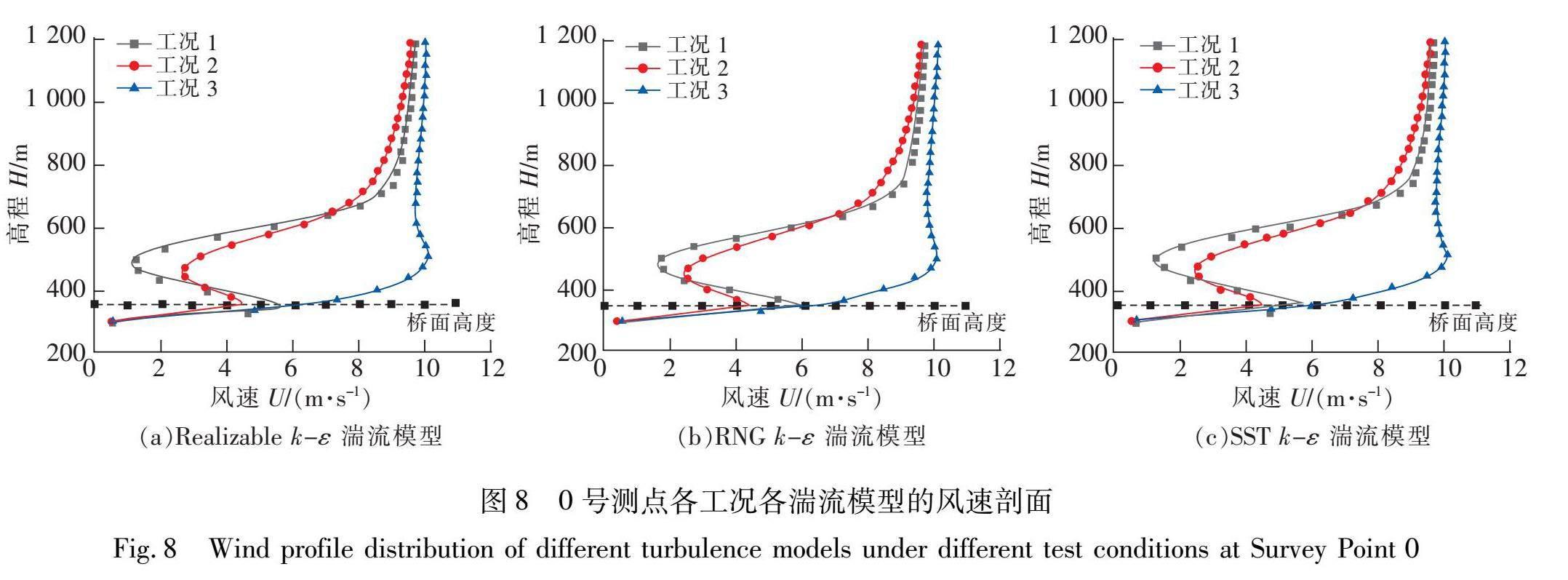
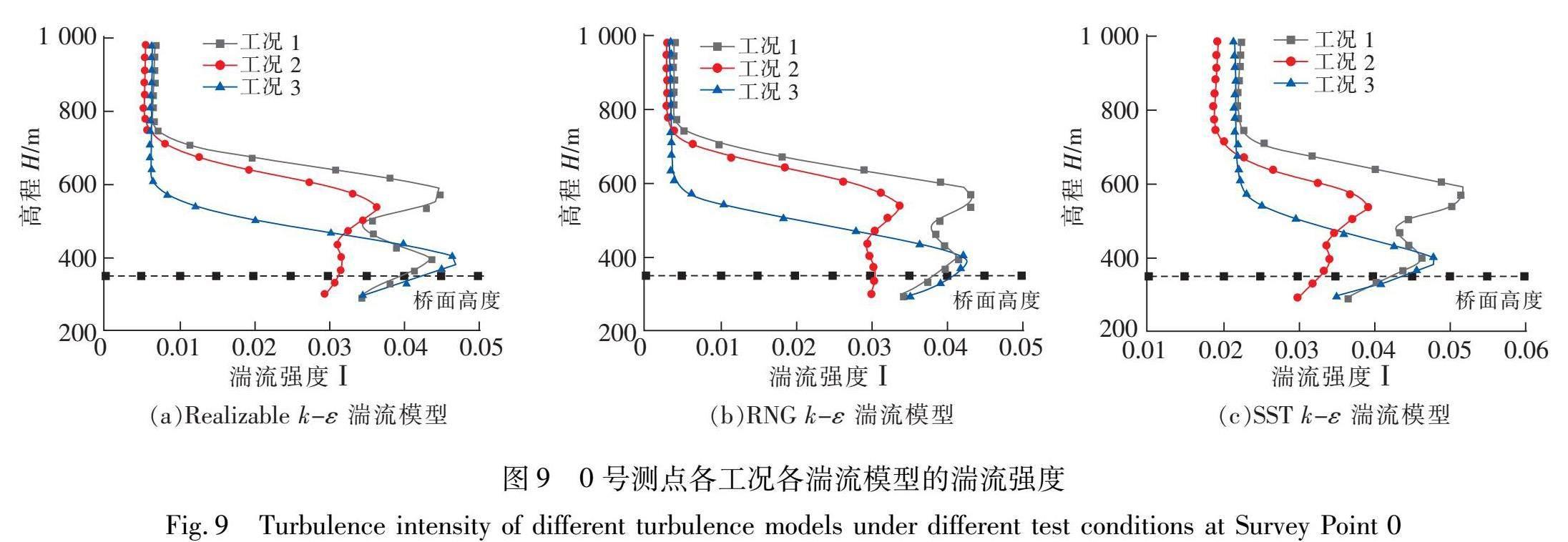
2.1 风速和湍流强度通过提取Ⅴ型峡谷3种湍流模型下3种工况和5个桥位测点风速的计算结果,分析风参数随着离地高度变化的分布规律。桥梁跨中0号测点风速和湍流强度高程剖面分布如图8、图9所示。根据峡谷地形下桥址区各工况典型位置处的竖向风速剖面和湍流强度分析得出,各湍流模型的变化趋势基本一致。跨中0号测点,在工况1和工况2的情况下,变化曲线走向一致但波动性较大,由于桥面两侧复杂山体的干扰作用,高程风速剖面分布呈Z型变化,在300~500 m范围出现两次拐点:340~500 m高程段内风速随高程增加而减小,高程达到500 m之后又随高度增加而增加,其中风速减小段可能是由桥面与两侧山体的相互作用影响,高程达到500 m之后风速大致符合规范中幂指数的增长规律;工况3在高程500 m以下,风剖面斜率较大,风速增长速度明显大于工况1和工况2。可能原因是:工况3的情况下山体的遮挡效应被削弱和峡谷两侧山体的挤压导致风速迅速增大,最大风速与最小风速的差值达到近0.93,梯度风高度为700 m;桥梁跨中位置的最大风速出现在RNG湍流模型上,达到10.2 m/s。
1号、2号和3号测点的风速和湍流强度高程剖面如图10、图11所示。1号测点和2号测点分别为茶洞岸和吉首岸四分之一跨处,3种工况下的风速剖面基本符合常规峡谷地形桥位风剖面的特征,湍流模型风速基本随高度增加而增加,在高度达到700~800 m时风速趋于不变。3号测点位于茶洞岸塔底山体的山顶处,此处有明显的山顶风速增大效应,在600~640 m迅速增大,最大风速为工况2下达到了11.8 m/s,比入口平均风速增大了18%,之后趋于平缓。
3种典型湍流模型下各监测点的湍流强度随高程递减的变化趋势基本一致,其中尤以跨中0号测点下工况1和工况2两种工况更为接近,变化趋势较为复杂,在300~700 m发生了3次突转,其他测点基本在高程范围内湍流强度随高度增加而减少,且在700 m后趋于平缓,这是由不同风向角下山体遮挡效应引起的;各测点在高程方向下湍流强度最大与最小差值分别为:0.808、0.882、0.833、0.756;桥面处湍流强度削弱基本一致,以0号测点为例:Realizable k-ε模型下3种工况桥面高度处湍流强度与高程方向下最大湍流强度相比,分别降低了12.8%、14.5%和8.7%,RNG k-ε模型下分别降低了12.0%、10.7%和5.6%,SST k-ε模型下分别降低了19.4%、16.9%和9.3%;桥塔处有增强,最大达到了12.6%。由以上分析矮寨大桥Ⅴ型峡谷梯度风高度大致为700 m左右,而抗风规范中矮寨大桥规定为D类地形,由规范查得梯度风高度为450 m,这与模拟所得结果有很大差异。这一差异说明规范中对地形粗略分类得出的风特性与实际山区桥址区风特性有所不同,在实际工程中应借助现场实测及风洞试验、模拟等手段分析具体风场特性。
2.2 最优数值模型选取
通过对Ⅴ型峡谷不同方向角和典型桥址位置处各湍流模型风特性随高程变化情况的分析,并借助已有学者的风洞试验结果[26],并设置不同粗糙高度(0,10,20 m)选出适合分析本地形风场特性的最优湍流模型。
2.2.1 流体壁面粗糙度
流体壁面粗糙度是Fluent对地形曲面计算域WALL的一种边界模拟条件,刻画了山体表面的黏滞阻力。通过改变他可以得出该底面边界参数对流场风特性的影响,以此达到模拟不同复杂地形下相适应的计算情况。研究所选的桥址区为起伏较大的丘陵地区,粗糙高度选择1 m,在利用Fluent设置壁面问题时应基于山体地表植被的覆盖情况,设置相应的粗糙度高度h,为了选出最适宜的粗糙度高度,此处选取0,10和20 m进行研究。
2.2.2 模拟结果与试验结果的比较
为得到最佳湍流模型,首先选取典型桥位跨中0号测点的平均风速与丁冬的风洞试验结果[26]进行比较,该风洞试验使用2块主体模型和4块缓和导风板设计出桥位地形对称的Ⅴ型峡谷地形模型,试验模型的缩尺比是1∶1 000,结果见表2。其次选择顺峡谷方向工况1下各测点风速计算结果进行对比,最后将该工况下不同壁面粗糙度下的湍流模型风速进行对比,分析数值模拟与风洞试验的差异,以此选取最适合本地形的湍流模型,工况1下各测点风速对比见表3。
从表2、表3可以看出,对于Ⅴ型峡谷来说,3种湍流模型计算出的风速差别不大,并且和风洞试验数据相差不大。在用风洞试验进行结果验证时,风速相对误差以不超过10%为宜,以上3种湍流模型都可适用,但RNG k-ε湍流模型计算出来的风速与风洞试验数据最为接近,故最终选择RNG k-ε湍流模型作为最佳方案。
将顺峡谷方向下典型测点处3种不同的壁面粗糙度的RNG k-ε湍流模型风速与风洞试验结果进行对比如图12所示。3种粗糙度下风速与风洞试验更为相近的是20 m,故选择该粗糙高度下的RNG k-ε湍流模型作为最佳湍流模型计算。
3 峡谷地形参数的影响
为研究地形参数对Ⅴ型峡谷地形桥位风特性的影响,在原Ⅴ型峡谷地形的基础上,通过改变离散点高程的纵坐标和经度来改变三维实际山体地形模型的高度和夹角,基于矮寨大桥数值模拟优选出来的湍流模型和粗糙度高度对峡谷周围风场特性开展研究。该三维山体地形模型的测点布置如图13所示,模拟结果选取典型的谷底0号测点和谷顶1号测点进行分析。
3.1 山体高度
由于在原地形山体高度的基础上,200 m以内风速的变化值比较明显,故建立山体高度增高120,80,40 m与减小40,80,120 m 6种不同山体的三维模型进行分析,将山体随高度变化的工况分别列为H1、H2、H3、H4、H5和H6。对Ⅴ型谷6种不同山体高度在风向角为0°和90°两种工况下各测点至计算域顶部风速的计算结果进行分析,提取0号测点与1号测点的山体风特性分布规律,以便于分析风速和湍流强度在不同山体高度的情况下随高度变化的分布规律。由此初步得出风速和湍流强度在不同山体高度各工况(风向角)下随高度的变化规律,如图14~图17所示。
从图14、图15可以看出,山谷谷底的近地面风速随着高度的增加会有一个过渡减缓期,减缓期高度在350~400 m,其影响程度可能受到峡谷两侧山体高度的增加而有所削弱,正是峡谷风紧缩升高的一个放大效应;山顶风速则会随着山体高度的增加有明显的增强效应;梯度风高度大约在700 m左右,在该高度处,山体高度越高,风速增强效果越大,最大达到12.56%。由规范可知在C类、D类地形中,梯度风高度为400 m和450 m,这与本节计算结果差距较大,说明实际工程中山体不能按规范简单归为4类。
从图16、图17可以看出,山谷的湍流强度在近地面400~500 m有一个停滞期,整体上看其强度会随着山体高度的增加有所下降;相反山顶的湍流强度则随山体高度的增加有所增强。
3.2 山体夹角为分析山体不同角度下桥址处的风特性变化规律,建立山体夹角分别为30°、60°、90°和120°的4种山体模型,分别由θ1~4表示,如图18所示。
提取Ⅴ型谷4种不同角度在风向角为0°和90°两种工况下谷底和谷顶至计算域顶部风速的计算结果,分析风速和湍流强度在不同山体角度下随山体高度变化的规律,如图19~图22所示。
从图19、图20可以看出,两个测点在风向角为0°和90°2种工况下的不同山体夹角风速随高程变化规律基本一致,都随着离地高度的增加而增加;山谷和山顶测点的风速都随着山体夹角的减小而增大,即山体越陡峭,风速值越大;梯度风高度大约在800 m左右,在该高度处,山体夹角越小,山体越陡峭,风速增强效果越大,最大达到了6.98%。由规范可知在C类、D类地形中,梯度风高度为400 m和450 m,这与分析结果差距较大,说明实际工程中山体不能按规范简单归为4类。
从图21、图22可以看出,山谷与山顶湍流强度均随着夹角变大,山体越平缓,其湍流强度越小,且山谷的湍流强度有一个200 m的过渡期,这种过渡期随着山体的陡峭程度越大越明显,可能原因是受到两侧山体的遮挡挤压影响。
3.3 Ⅴ型峡谷湍流强度与现行抗风规范的对比
通过矮寨大桥在0号测点工况一的数值计算结果与抗风规范离地高度160 m以下设计湍流强度的对比,如图23所示,峡谷地形下的数值湍流强度较抗风规范中4类地表有明显的差异,在40 m以下,更接近于D类地表规范,在20 m高度处两值最为接近,仅相差2.59%;而在40 m以上高度,峡谷地形的湍流强度较规范中4类地形的差异均较大,最大在离地150 m处相差32.06%。这些结果进一步说明不同峡谷地形下地形参数变化值幅度大,在工程设计中应进一步借鉴实测数据、风洞试验或数值风洞的结果,同时结合规范综合考量,确保选取的湍流强度是正确的。
综合分析可知,随山体高度的增高,山谷处湍流强度呈现下降趋势,山顶处湍流强度随高度增加增强;随山体夹角变大,山谷和山顶处湍流强度下降。受山体两侧高度和夹角的影响,山体高度变化对湍流强度的影响效应明显大于山体夹角变化的影响。
3.4 山区峡谷桥面设计基准风速的推算与比较
依据桥梁地理位置,选取距离桥址较近的吉首市气象站作为基本风速参考站点,查《公路桥梁抗风设计规范》(JTG/T 3360-01—2018)附录A,Ⅴ型峡谷地形所处的吉首地区不考虑风向地面以上10 m高度处100 a重现期、10 min平均的年最大风速为24.3 m/s。
以桥址附近的“虚拟标准气象站”基本风速作为峡谷边界入口的基本风速,借用现有研究的经验关系式计算建于Ⅴ型峡谷桥面的设计基准风速,经验关系为[27]
Ud=U10
1.0+
πH5(B1+B2)
=kU10
(1)
式中 Ud为设计基准风速,m/s;U10为虚拟气象站的基本风速,m/s;H为桥面高度,m;B1为峡谷上口处宽度,一般取桥长,m;B2为峡谷下底面宽度,m;
k为峡谷效应修正系数。
根据以上修正公式,参考矮寨大桥设计(图24):
U10=24.3 m/s
,B1=1 000 m,B2=250 m,H=340 m,得k=1.171。
从而桥面高度处的设计基准风速:
Ud=1.171×24.3 m/s=28.46 m/s
。
由该经验公式计算得到的桥梁抗风设计基准风速与文献[17]中的拟合计算公式基本一致,与文献[28]设计阶段的桥面基准风速34.9 m/s相差18.5%,说明在现场实测风速数据难以获得的山区地带,可参考经验公式初步获得跨越Ⅴ型峡谷桥梁的基准风速。
根据以上初步判断的地表类型并利用现有最新的抗风规范计算该桥面高度的设计基准风速为
Ud=kf
Z10
α0Us10
(2)
式中 kf为抗风风险系数;α0为桥址处的地表粗糙度系数;
Z为桥面高度,m;
Us10为桥梁设计基本风速,m/s。
桥梁设计基本风速Us10计算式为
Us10=kcU10
(3)
式中 kc为基本风速地表类别转换系数。
根据《抗风规范》可知,kf=1.0,α0=0.3,kc=0.564,从而桥梁设计基本风速:
Ud=1.0×
34010
0.3×0.564×24.3 m/s=39.48 m/s。
经验公式与现有规范相差27.9%,因此在进行峡谷地形桥址处的设计风参数计算时,应综合考虑桥梁抗风规范、相关经验公式,并可借助桥梁工程研究中常用数值模拟方法[29]作为参考来进一步提高其准确性。
4 结 论
1)受峡谷地形的影响,在3种湍流模型综合对比并考虑地表粗糙度对近地面风场干扰的条件下,该桥址地区范围内地形最优模型为流体壁面粗糙度20 m的RNG k-ε模型,此模型可为后续类似地貌下桥梁结构的风场数值模拟研究提供参考。
2)受山体高度和山体夹角两种地形参数的影响,该类峡谷地形在两参数变化时的梯度风高度分别为700 m和800 m左右,大于规范中4类地表的取值,且在离地高度40 m范围内,湍流强度更接近于D类地表;在梯度风高度处,山体高度和夹角对风速增强影响范围分别为2.37%~12.56%和1.24%~6.98%,明显山体高度对此峡谷地形的影响效果要大于山体夹角的变化,同时由于两侧山体的干扰,湍流强度在一定高度处(400~500 m)会有一段停滞期。
3)由于峡谷两侧山体的遮挡作用,风剖面分布呈Z型,在300~500 m出现两次拐点,之后风速大致符合规范中幂指数的增长规律;根据峡谷地形参数分析,两侧山体夹角越小,风速值越大,山体高度越高,风速值增长越快。
4)依据Ⅴ型峡谷桥梁的经验公式得出的桥面高度处的设计基准风速与按抗风规范计算得出的风速相比,更加接近实际桥址区。因此,针对此类地形风洞试验或实际工程项目的研究,在没有现场实测数据支撑时,可以通过“数值风洞”计算得出风速数据及各类风场特性作为参考。
参考文献(References):
[1]
UCHIDA T,OHYA Y.Large-eddy simulation of turbulent airflow over complex terrain[J].Journal of Wind Engineering and Industrial Aerodynamics,2003,91(1-2):219-229.
[2]BULLARD J E,WIGGS G F S,NASH D J.Experimental study of wind directional variability in the vicinity of a model valley[J].Geomorphology,2000(35):127-143.
[3]刘黎阳,张志田,汪志雄,等.不同规模地形模型对某山区桥梁设计风特性确定的影响[J].实验流体力学,2018,32(6):49-54.
LIU Liyang,ZHANG Zhitian,WANG Zhixiong,et al.
Scope effects of terrain models on wind properties design of a bridge located at mountainous area[J].Journal of Experiments in Fluid Mechanics,2018,32(6):49-54.
[4]周继,王新国,刘志文,等.大跨度山区桥梁风特性数值模拟及试验研究[J].铁道科学与工程学报,2022,19(4):995-1003.
ZHOU Ji,WANG Xinguo,LIU Zhiwen,et al.Numerical simulation and experimental study on wind characteristics of long span bridge in mountainous area[J].Journal of Railway Science and Engineering,2022,19(4):995-1003.
[5]张向旭,郑史雄,唐煜,等.山区峡谷大跨度拱桥桥址区风参数数值模拟研究[J].铁道科学与工程学报,2018,15(2):398-406.
ZHANG Xiangxu,ZHENG Shixiong,TANG Yu,et al.Numerical study on wind parameters for a long span arch bridge in the area of a gorge[J].Journal of Railway Science and Engineering,2018,15(2):398-406.
[6]李永乐,遆子龙,汪斌,等.山区Y形河口附近桥址区地形风特性数值模拟研究[J].西南交通大学学报,2016,51(2):341-348.
LI Yongle,TI Zilong,WANG Bin,et al.Numerical simulation of wind characteristics over bridge site near Y-shaped river junction in mountainous area[J].Journal of Southwest Jiaotong University,2016,51(2):341-348.
[7]于舰涵,李明水,廖海黎.山区地形对桥位风场影响的数值模拟[J].西南交通大学学报,2016,51(4):654-662.
YU Jianhan,LI Mingshui,LIAO Haili.Numerical simulation of effect of mountainous topography on wind field at bridge site[J].Journal of Southwest Jiaotong University,2016,51(4):654-662.
[8]薛亚飞.复杂地形桥位风场实测与CFD数值模拟[D].长沙:湖南大学,2015.
XUE Yafei.Field measurement and CFD numerical si-mulation of wind over bridge site with complex terrain[D].Changsha:Hunan University,2015.
[9]孙亭亭,杨吉新,黎建华,等.基于脉动风作用下的大跨度桥梁拉索风场数值模拟[J].山东农业大学学报(自然科学版),2018,49(5):809-814.
SUN Tingting,YANG Jixin,LI Jianhua,et al.Numerical simulation of wind field on large span bridge cable based on pulsating winds[J].Journal of Shandong Agricultural University(Natural Science Edition),2018,49(5):809-814.
[10]王铁强.实际地形下风场CFD模拟与参数分析[D].广州:中山大学,2009.
WANG Tieqiang.CFD wind field simulation and para-meter analysis over natural terrain[D].Guangzhou:Sun Yat-sen University,2009.
[11]于涛.山区峡谷风特性的数值模拟与现场实测的对比研究[D].湘潭:湖南科技大学,2014.
YU Tao.Study on wind-environment numerieal simulation and field measurement about canyon[D].Xiangtan:Hunan University of Science and Technology,2014.
[12]张玥.西部山区谷口处桥位风特性观测与风环境数值模拟研究[D].西安:长安大学,2009.
ZHANG Yue.Field investigation and wind-environment numerical simulation of bridge site in the western gap of valley areas[D].Xian:Changan University,2009.
[13]唐昂.基于实际峡谷地形的近地风场特性研究[D].杭州:浙江理工大学,2015.
TANG Ang.Study on characteristcs of wind field in ground layer on actual canyon terrain[D].Hangzhou:Zhejiang Sci-Tech University,2015.
[14]唐金旺.喇叭口地形桥址强风特性风洞试验及CFD模拟研究[D].西安:西安科技大学,2017.
TANG Jinwang.The strong wind characteristics at bridge site of Trumpet-shaped topography with wind tunnel test and CFD simulation[D].Xian:Xian University of Science and Technology,2017.
[15]姚剑锋,沈国辉,姚旦,等.峡谷和垭口地形风场特征的CFD数值模拟[J].哈尔滨工业大学学报,2016,48(12):165-171.
YAO Jianfeng,SHEN Guohui,YAO Dan,et al.CFD-based numerical simulation of wind field characteristics on valley and col terrain[J].Journal of Harbin Institute of Technology,2016,48(12):165-171.
[16]高亮.内陆强风特性的现场实测与模拟[D].西安:长安大学,2012.
GAO Liang.Simulation and field measurement of the characters of strong wind in inner land of China[D].Xian:Changan University,2012.
[17]洪新民,郭文华,熊安平.山区峡谷风场分布特性及地形影响的数值模拟[J].长安大学学报(自然科学版),2017,37(5):56-64.
HONG Xinmin,GUO Wenhua,XIONG Anping.Numerical simulation of distribution characteristics of wind fields and terrains influence in mountain canyon[J].Journal of Changan University(Natural Science Edition),2017,37(5):56-64.
[18]冯林.基于峡谷地形的风场数值模拟研究[D].杭州:浙江理工大学,2017.
FENG Lin.Numerical simulation of wind field based on canyon terrain[D].Hangzhou:Zhejiang Sci-Tech University,2017.
[19]楼文娟,刘萌萌,李正昊,等.峡谷地形平均风速特性与加速效应[J].湖南大学学报(自然科学版),2016,43(7):8-15.
LOU Wenjuan,LIU Mengmeng,LI Zhenghao,et al.Research on mean wind speed characteristics and speed-up effect in canyon terrain[J].Journal of Hunan University(Natural Sciences),2016,43(7):8-15.
[20]陈平.地形对山地丘陵风场影响的数值研究[D].杭州:浙江大学,2007.
CHEN Ping.Numerical study of terrain influence on the airflow over hilly land[D].Hangzhou:Zhejiang University,2007.
[21]李正昊,楼文娟,章李刚,等.地貌因素对垭口内风速影响的数值模拟[J].浙江大学学报(工学版),2016,50(5):848-855.
LI Zhenghao,LOU Wenjuan,ZHANG Ligang,et al.Numerical simulation of effects of topographic factors on wind speed in col[J].Journal of Zhejiang University(Engineering Science),2016,50(5):848-855.
[22]BOWEN A J,LINDLEY D.A wind-tunnel investigation of the wind speed and turbulence characteristics close to the ground over various escarpment shapes[J].Boundary-Layer Meteorology,1977,12(3):259-271.
[23]CAO S,TAMURA T.Experimental study on roughness effects on turbulent boundary layer flow over a two-dimensional steep hill[J].Journal of Wind Engineering and Industrial Aerodynamics,2006,94(1):1-19.
[24]LUBITZ W D,WHITE B R.Wind-tunnel and field investigation of the effect of local wind direction on speed-up over hills[J].Journal of Wind Engineering and Industrial Aerodynamics,2007,95(8):639-661.
[25]童祎巍.矮寨大桥桥址区脉动风特性及高斯条件模拟研究[D].湘潭:湖南科技大学,2015.
TONG Yiwei.Fluctuating wind characteristics of Aizhai bridge area and of its gaussian condition simulations[D].Xiangtan:Hunan University of Science and Technology,2015.
[26]丁冬.典型山区地形桥位良态风特性研究[D].长沙:湖南大学,2017.
DING Dong.Study on normal wind characteristics over bridge sites with typical mountainous terrain[D].Changsha:Hunan University,2017.
[27]
王凯,廖海黎,李明水,等.山区峡谷桥梁设计基准风速的确定方法[J].西南交通大学学报,2013,48(1):29-35.
WANG Kai,LIAO Haili,LI Mingshui,et al.Determination method for basic design wind speed of mountainous-valley bridge[J].Journal of Southwest Jiaotong University,2013,48(1):29-35.
[28]陈政清,李春光,张志田,等.山区峡谷地带大跨度桥梁风场特性试验[J].实验流体力学,2008(3):54-59,67.
CHEN Zhengqing,LI Chunguang,ZHANG Zhitian,et al.Model test study of wind field characteristics of long-span bridge site in mountainous valley terrain[J].Journal of Experiments in Fluid Mechanics,2008(3):54-59,67.
[29]谷拴成,姚博语,任翔,等.煤矿输煤栈桥抗振性能及动力响应[J].西安科技大学学报,2022,42(1):8-15.
GU Shuancheng,YAO Boyu,REN Xiang,et al.Research on resonance and dynamic response of coal conveying trestle in coal mine[J].Journal of Xian University of Science and Technology,2022,42(1):8-15.
(责任编辑:刘洁)
