基于自适应交叉策略遗传算法的非空货位分配方案优化研究

何金涛 杨中华

摘 要：针对“货到人”拣选系统的补货环节，考虑仓库起始状态非空条件下的货位分配问题，将货架现存商品种类及数量信息与订单包含的商品种类及数量信息进行比对，做出商品分配位置以及上架数量决策，以所有货架上的商品相似度总和最大化为目标，构建了整数非线性规划模型，并设计了自适应交叉策略的遗传算法进行求解，以问题实际约束对染色体生成、交叉和变异操作进行设计。通过随机算例来对算法进行测试，结果表明文章设计的算法能够有效解决其实状态非空的货位分配问题。

关键词：“货到人”拣选；货位分配；遗传算法

中图分类号：F252；TP18 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.10.003

Abstract： In view of the replenishment process of the "goods to people" picking system，considering the space allocation problem under the condition that the initial state of the warehouse is not empty，the type and quantity information of the existing goods on the shelf is compared with the type and quantity information of the goods contained in the order to make the decision of the distribution location and the number of goods on the shelf. An integer nonlinear programming model was constructed with the goal of maximizing the sum of similarity of goods on all shelves，and an adaptive crossover strategy genetic algorithm was designed to solve the problem. The chromosome generation，crossover and mutation operations were designed according to the practical constraints of the problem. The algorithm is tested by a random example，and the results show that the algorithm designed in this paper can effectively solve the problem of non-empty space allocation.

Key words： "goods to people" picking; space allocation; genetic algorithm

0    引    言

近年来，随着消费者需求的多样化转变，电子商务呈现出高频率、多品种、小批量的特点，对企业的仓储、分拣、订单处理等工作提出了更高的要求。作为一种新兴的拣选处理模式，“货到人”拣选系统（Robotic mobile fulfillment systems，RMFS）采用AGV（Automated Guided Vehicle）、AMR（Autonomous Mobile Robot）、AGC（Automated Guided Cart）等设备[1]将储存货物的货架、托盘等载体搬运至人工拣选站实现“货到人”的拣选。这种“货到人”拣选模式最早于2012年由Amazon应用于仓储分拣系统中，目前国内的“货到人”拣选系统的实际运用已经有阿里菜鸟联盟智能仓、京东天狼货到人系统和快仓等。与传统的“人到货”拣选模式类似，“货到人”系统也需要解决货位分配、订单分批、任务指派和路径规划等[2]问题。其中，作为拣选流程中的先决步骤，仓储系统中的货位分配工作无疑影响着后续工作的组织和效率。目前已经有很多学者对“货到人”拣选系统的货位分配展开了大量研究，主要集中在问题模型的约束细化、优化目标的确定以及求解方法的改进等方面[3]。

在问题模型的约束细化方面，Mirzaei 等[4]提出了规格相同的货位对于不同种商品的容量上限不同，更加贴合于现实问题中的标准化货位对应不同规格的商品。李英德[5]考虑了SKU相关性的装箱问题与货位分配的协同优化，设计了“SKUs对”相关性位置变换策略，并使用SAC算法和NFDP算法针对性地分别求解装箱问题和货位指派问题。杨雅婷等[6]在交叉存取拣选模式下考虑动态时间阈值和动态距离阈值，以拣选任务为主，在阈值约束下考虑是否执行存放任务并判断货物存放位置，同时优化了订单拣选顺序及货物上架位置的决策，实现了“货到人”拣选系统中的动态拣选与货位分配任务同时进行。张雪等[7]考虑了仓库非空状态下一品多位的货位分配问题，同时考虑滞销商品的下架操作和商品的上架位置指派优化，采用贪婪算法生成初始解，再采用粒子群优化算法求解该问题。

同时，由于不同行业对仓储运行的需求不尽相同，所以在进行货位分配决策时想要达到的目标也比较多元，常见的货位分配目标有单位时间的吞吐量最大、批次订单的拣选时间最短、单位货架的稳定性最高、货架上商品关联度最高等。Wang等[8]在考虑货架承重约束以及高度约束的同时以货架重心最低为目标，采用层次遗传算法求解货位分配问题。袁瑞萍等[9]以最小化货架搬运次数以及最小化机器人总拣选路程为目标，并结合商品分配到货架以及货架位置的两阶段决策思想，设计两阶段启发式算法进行求解。包菊芳等[10]以同一货架上SKU的总关联度最大为目标，采用FP-Growth算法以及聚类方法进行求解。周亚云等[11]综合考虑了商品需求关联度与周转率，通过计算商品关联性和相似性，采用基于拉普拉斯矩阵分解的SC算法中引入K-Means++算法对商品进行聚类完成货位分配决策。

在求解方法的改进方面，主要采用的方法有排队网络、启发式聚类、启发式算法以及一些仿真优化等。Keung等[12]以改进的A*算法计算拣选过程中所有货架的总移动距离，并以此衡量包括K-means聚类，高斯混合模型聚类，贝叶斯高斯混合模型聚类等在内的9种货位分配的聚类方法的优化效果。胡祥培等[13]通过对商品关联网络的构建、分析和聚类三个阶段来解决一品多位的商品货位分配问题。翟梦月等[14]同时考虑商品种类和数量的双重关联，以拣选批次订单货架移动次数最小为目标，设计了结合模拟退火思想的变邻域搜索算法进行求解。王征等[15]在已知未来订单信息以及货架上储存的商品种类信息的情况下建立货架热度和货架关联度模型，设计了双层邻域变换的禁忌搜索启发式算法来优化货架位置。

对于“货到人”系统中的商品分配到货架的货位分配问题，目前的研究大多都是针对仓库起始状态为空的归零优化，而在实际的仓储条件下，系统中的补货过程往往不是在仓库全部为空的状态下进行的。针对某一特定时刻的货位分配问题，本文考虑仓库起始状态非空，并根据订单信息来确定特定商品是否需要进行下架，以及某种商品实际所需要的货位数量，在不对货架进行清空操作的情况下完成商品上架位置及数量的决策。同时，结合实际的货位对于商品的容量上限以及商品的需求量，以最大化所有货架上的商品关联度为目标构建的整数非线性规划模型，并设计了针对起始状态非空的0-1矩阵编码的遗传算法进行求解。由于染色体规模过大，为了保证搜索范围与搜索精度，在交叉操作中设计了自适应交叉策略。

1    问题描述与分析

“货到人”拣选系统（RMFS）主要由可移动式货架、机器人、通道、拣选台等构成。RMFS的作业流程是：根据一定的分配策略将商品分配到各个货架以及将货架分配到仓库中的相应位置，收到订单后，按照顺序或者批次将订单任务进行排序或者分批，并将货架搬运任务分配给仓库内的机器人执行，由机器人将货架搬运至拣选台，再由人工完成拣选任务，机器人再按照相应的策略将货架重新搬运至储存区中的相应位置[2]。在本文研究的动态货位分配问题中，考虑货架初始状态非空，即仓库中的某些货架的某些货位中已经存放有若干种商品，需要对原始仓储状态进行分析来进行货位分配工作，其中可能包括滞销商品的下架工作，非空但未满的货位的分配数量决策等。这样的考虑更加符合当前电子商务模式下消费者高频率、多品种、小批量的消费需求。

“货到人”拣选系统的动态货位分配问题描述如下：该系统中有N个可移动货架，每个货架有L个货位，每个货位的规格相同，但是对于不同种类商品的容量限制LP不同[4]。现存放有若干种（1，P）商品，且每个货架上存放的商品种类及数量已知，其中存在某些商品可能不会出现在未来的订单集合中，需要进行下架操作，同时订单中可能会出现一些新种类的商品需要上架。未来订单包含的商品种类及数量已知，每种商品可以分散储存在不同的货架中（即“一品多位”策略），但是同一个货架中的两个货位不能出现同种商品。

1.1    模型假设

未来时段的订单信息包含所需商品种类及数量，其中每个订单包含一种及以上种商品；仓库货架原始状态不全为空；每个货架规格相同，但是对于不同种类商品的容量不同[4]；每种商品的货位容量限制能够满足订单对于该种商品的需求，即不存在某个订单需要搬运两个货架来满足其中一种商品的需求；每种商品可以分配到多个货架上，一个货位只能存放一种商品；订单不可拆分；每个货架在仓库中的位置固定，即货架完成拣选后仍返回原来的位置；订单上出现的商品至少存放在一个货架的某个储位上。

1.2    符号说明

根据Yuan等[16]的研究，如表1所示，当库存量约为平均需求量的四倍时，极少出现缺货情况，又因为我们考虑仓库初始状态非空，我们需要最终仓库中的库存量为：

其中每种商品的总需求量可以表示为：

所以，可以计算出每种商品所需要的货数Dp为：

在此动态货位分配问题中，考虑货架原始状态非空，根据订单信息与库存信息之间的差异可以得出可能存在的需要下架的滞销商品集合α，以及需要上架的新品种商品集合β（存在于货架上但并未出现在未来订单中的商品种类属于滞销商品，存在于订单中但货架上并未存放的商品属于新品种商品）。

根据文献对于商品关联度的描述，我们定义商品之间的关联度计算为，其中为同时包含商品和商品的订单数量，为包含商品的订单数量，为包含商品j的订单数量[7]。

1.3    非线性整数规划模型

决策变量：

整数变量，商品在货架上的分配数量。

以最大化所有货架中的商品关联度为目标函数的非线性整数规划模型如下。

约束条件如下。

其中，约束条件（1）表示分配到货架上的商品数小于等于货架上的空位数加上原有商品占用的货位和滞销商品下架产生的空货位。约束条件（2）表示至少为每一种商品（滞销商品除外）分配一个货位。约束条件（3）表示当商品已经存放于货架上时，不论存放数量是否已经达到该商品的货架容量上限，都认为该商品分配至该货架。约束条件（4）表示每个货架上分配的商品种类数小于等于货位数。约束条件（5）表示为商品分配的货位数大于等于商品需要的货位数。约束条件（6）和（7）规定了商品补充后的库存量与需求量的关系：若货架上已经存放了商品，但存放数量小于，根据约束条件（6），我们分配件该商品至该货架，使得该货架存放的该商品数量达到该商品的货位容量上限；若分配商品到没有存放该种商品的货架时，分配件至该货架，即使未分配满时已经可以满足需求仍然分配该货位至满容量，这样就保证了最终存放商品的每一个货位都存放了件商品。约束条件（8）和（9）约束了变量的取值。

2    基于自适应交叉策略的遗传算法设计

货位分配问题属于“一品多位”的指派问题，“一品多位”的货位分配问题已经被证明属于NP-hard问题[13]。本文研究的货位分配问题由于货架初始状态非空，商品的上架位置决策受到约束更多，所以，针对上述的初始状态非空的货位分配问题需要设计求解算法。按照问题描述，我们需要获取起始状态下每个货架存放的商品种类及数量，根据订单信息确认滞销商品种类以及计算商品之间的关联度、每种商品的需求量、所需要的货位数量。根据所需的变量的数据类型，本文设计了针对该问题的基于自适应交叉策略的遗传算法。

2.1    染色体编码

根据货位分配问题的特点，本文采用0-1矩阵编码来构造货位分配方案染色体：每一个的染色体代表一种货位分配方案，其中每一行代表一个货架，每一列代表一种商品。由于仓库起始状态下的商品位置固定，且滞销商品需要下架，染色体的生成需要根据仓库起始状态来确定。从仓库起始状态生成染色体的过程（5种商品、10个货架）如图1所示。

图1中左图表示仓库起始状态下有编号为1、2、4的三种商品存放于货架中，又根据订单信息得到了新品种商品3和5，并且商品1未出现在未来订单中，属于需要下架的滞销商品。根据这些信息，生成染色体时先将滞销商品列全部变为0，然后在固定初始库存中非滞销商品位置的情况下随机填充每一行（每一个货架）存放的商品至货架中的货位数上限L（上例假设为3），并且针对上一章提出的每一种商品需要的货位数Dp，我们还定义了每个商品列（滞销商品除外）包含元素“1”的数量大于等于其Dp值。最后我们就得到了一个可行的货位分配方案染色体，其中每一个位置的元素对应着非线性整数规划模型中的决策变量。

2.2    适应度函数

本文将遗传算法的适应度计算定义对每个染色体（货位分配方案）遍历每一行（每一个货架），计算每一行中包含的每对商品之间的关联度加总，再对单个个体的每一行的关联度加总，得到该种分配方案下的总关联度作为该个体的适应度值。

2.3    精英保留策略

在基于传统交叉算子的遗传算法中，在迭代后期每一代的最优适应度值会出现较大波动，甚至无法达到收敛，基于这种情况我们引入精英保留策略，保留一定规模的适应度最高的个体不参与交叉和变异操作直接进入下一代种群，我们设定10%的概率保留精英个体。

2.4    自适应交叉策略

针对前文所述的染色体需要满足的约束条件，本文设计了一种自适应交叉策略，包含两种交叉算子，分别是传统遗传算法所使用的两个父代染色体交换部分基因的双亲交叉算子（下文简述为“传统交叉”），以及在单个染色体内进行交叉操作的单亲进化交叉算子[17]（下文简述为“单亲交叉”）。

2.4.1    传统交叉

传统遗传算法所使用的交叉算子都是在两个父代染色体之间进行基因交换来进行种群更新的，本文针对非空状态的货位分配问题的染色体设计的交叉算子运作流程如图2所示。

固定起始状态商品位置的“1”元素以及滞销商品列不参与交叉，计算其它位置的基因数量，随机选择其中一半的位置，交换两个父代这些位置的基因。在进行上述规则的交叉后会影响子代染色体的基因规则，可能有出现子代染色体中的某些行（货架）内出现超过货位数L的“1”（商品），所以需要对交叉后的染色体进行修正后才能产生符合约束的子代染色体，这个修正过程将每一行的“1”的数量调整到货位数量的同时，保证每一列的“1”符合商品所需要的货位数量约束。

2.4.2    单亲交叉

根据单亲进化遗传算法的思想，本文设计的单亲交叉策略只在单个染色体内进行，不同于传统交叉使用的先交叉再修正的思想，在单亲交叉中为了提高搜索精度，本文直接按照染色体约束选择合适的基因位置进行交叉，交叉操作流程如图3所示。

首先随机选择染色体中的两行，遍历这两行中除滞销商品列的位置寻找两个可交叉位置，使得这两行对应位置的元素分别相反，交换这两行对应位置的元素，这样既保证了每一个货架存放的货物种类数不会超过货位数，又保证了每种商品被分配到所需要的货位数量。

2.4.3    自适应交叉策略设计

我们注意到传统遗传算法在收敛的过程中每一代的最优值变动较大，虽然在迭代前期收敛速度较快，但是在收敛后期，最优适应度值时不时会发生不规则波动，导致每一代的种群更新速度较慢，这是由于传统交叉算子所选择的交叉范围比较大的缘故。基于此，本文设计了一种自适应交叉策略，在迭代初期更多地选择传统交叉策略以扩大搜索范围加快迭代速度，在迭代后期更多地选择单亲交叉策略增加搜索精度。具体而言，根据迭代进程以线性递减的概率选择传统交叉策略，每一代选择传统交叉策略的概率Ptro表示如下。

其中，表示最大迭代次数，表示当前迭代次数。

2.5    变异操作

根据上述染色体约束，本文采用成对基因突变变异算子进行变异操作，即随机选择染色体中的一行，将其中一个非滞销商品列的“0”元素变成“1”，再将一个非起始状态固定位置的“1”元素变成“0”，以此保证每行元素符合单个货架的货位数约束。然后根据每列（滞销商品除外）是否符合每种商品所需货位数约束进行修正，若变异后出现某一列（商品）的“1”元素的数量（为该种商品分配的货位数）小于其所需货位数，则在该列元素为“0”的位置随机选择一个变成“1”，再将产生变换的行中某种已分配的货架数大于该种商品所需货位数的商品的“1”变成“0”，若该行中所有商品都不符合上述变换条件，则选择其他行的其他商品。

如图4所示，随机选择了第三行进行变异，假设第二种商品计算出所需要的货位数为7个货位，经过变异之后第二列只为该种商品分配了六个货位，这时需要对染色体进行修正，随机选择了第二列第七行的“0”元素变为“1”，再遍历该行中所有的商品（起始固定位置商品除外）是否已经分配超过其所需货位数的商品，我们搜索到第五种商品需要8个货位，已经分配了10个货位，所以该行将第五种商品的“1”变为“0”。

3    随机算例仿真

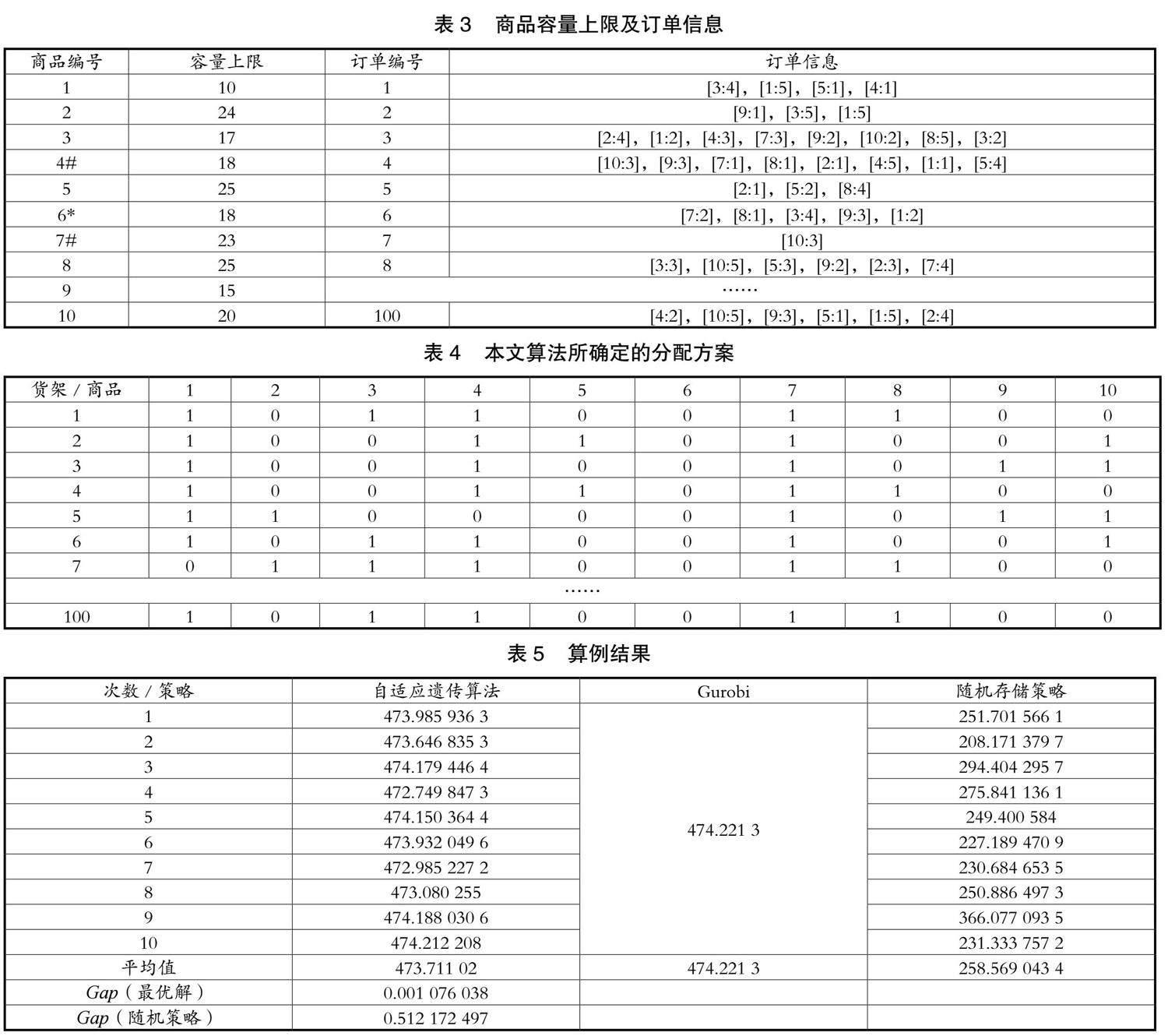
以一个小规模算例为例，首先对100个容量为5的货架（500个货位）按照0.8的概率随机生成空位，并针对每种商品生成商品的货位容量上限为10～25的随机数，对于存放商品的位置随机选择非新品种商品，并设置现存数量为5到该种商品容量上限的随机数，得到起始状态下的仓储状态如表2所示，其中每个货位第一位表示存放的商品种类，第二位表示该种商品的存放数量；*表示滞销商品（不出现在订单中），#表示新品种商品（不出现在起始仓储状态中）。然后按照订单数量生成随机订单，其中每个订单包含1～9（一种滞销商品除外）种商品，每种商品的订购数量为1～5之间的随机数，生成的每种商品的货位容量上限以及订单信息如表3所示。

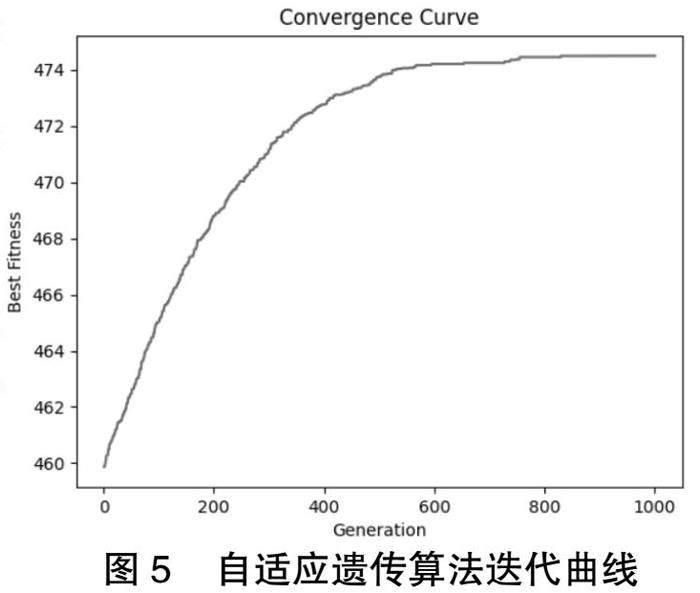
对该算例采用自适应遗传算法进行求解，实验参数设置为：种群规模Ps=100、最大迭代次数Gmax=1 000、交叉概率Pc=0.8、变异概率Pm=0.1、精英保留概率Pe=0.1。进行十次求解的相似度平均值为473.711 02，输出的分配矩阵如表4所示，可以观察出算法求出的解同样符合约束条件。对该算例的每一次迭代的效果如表5所示，其中Gap（最优解）表示算法解与Gurobi求解出的全局最优解的差距，Gap（随机策略）表示算法求解的分配方案与随机存储策略的相似度值差距。可以看出在该算例中本文提出的算法较之于随机存储策略优化效果达到51.21%，与全局最优方案差距保持在0.1%左右，有着较好的收敛效果，算法的收敛曲线如图5所示。

4    总结与展望

本文针对起始状态非空的“货到人”系统的货位分配问题，考虑的商品的滞销下架、货位对于商品的容量约束以及从订单中得出具体的货位分配数量，以所有货架上的相似度总和最大化为目标，设计了0-1矩阵编码的自适应交叉策略遗传算法进行求解，并在算法中为了贴合该问题的实际约束重新设计了染色体生成、交叉和变异规则，在交叉部分设计了针对0-1矩阵编码的染色体的传统交叉与单亲交叉混合的交叉策略，有助于在收敛前期扩大搜索范围，在收敛后期增加搜索精度。实验结果表明，本文设计的自适应交叉策略的遗传算法能够有效解决起始状态非空的货位分配问题。

但是，本文仅考虑了大批订单下的货架商品相似度，并未考虑到在不同分批策略下的货位分配目标是否需要改进，对于后续的研究，可以在此基础上考虑拣选任务与补货任务同时进行的交叉存取规则下的货位分配问题，以及实时状态监控与更新，实现更加动态的货位分配决策优化。

参考文献：

[1] DA COSTA BARROS T R，NASCIMENTO T P．Robotic Mobile Fulfillment Systems：A survey on recent developments and      research opportunities [J/OL]．Robotics and Autonomous Systems，2021，137．[2023-07-23].https：//doi.org/10.1016/j.robot.2021.103729.

[2] 徐翔斌，马中强．基于移动机器人的拣货系统研究进展[J]．自动化学报，2022，48（1）：1-20．

[3] 雷斌，王菀莹，赵佳欣．货位分配优化研究综述[J]．计算机工程与应用，2021，57（1）：48-55．

[4] MIRZAEI M，ZAERPOUR N，DE KOSTER R B M．How to benefit from order data：Correlated dispersed storage assignment    in robotic warehouses [J]．International Journal of Production Research，2022，60（2）：549- 568．

[5] 李英德．波次分区拣货时装箱与货位指派问题协同优化的模型与算法[J]．系统工程理论与实践，2013，33（5）：1269-1276．

[6] 杨雅婷，许瑞，陆晓芬，等．动态阈值下的交叉存取优化问题研究[J]．工业工程与管理，2023，28（3）：83-95．

[7] 张雪，周丽，路雪鹏，等．基于“货到人”拣选系统的动态货位分配研究[J]．包装工程，2022，43（15）：247-257．

[8] WANG Xuelian，Xu Man，XIAO Jing，et al．Optimization of goods locations assignment of automated warehouse on hierarchic       genetic algorithm[J]．Applied Mechanics and Materials，2014，510：265-270．

[9] 袁瑞萍，王慧玲，李俊韬，等．基于移动机器人的订单拣选系统货位优化模型和算法研究[J].系统科学与数学，2020，40（6）：1050-1060.

[10] 包菊芳，王丽．基于SKU关联度的储位优化问题研究[J]．数学的实践与认识，2021，51（14）：31-40．

[11] 周亚云，项前，余崇贵，等．考虑物料需求关联与周转率的仓储货位优化方法[J]．东华大学学报（自然科学版），2020，46（3）：414-420.

[12] KEUNG K L，LEE C K M，JI P．Data-driven order correlation pattern and storage location assignment in robotic mobile fulfillment and      process automation system[J/OL]．Advanced Engineering Informatics，2021，50．[2023-08-01]．https：//doi.org/10.1016/j.aei.2021.101369.

[13] 胡祥培，丁天蓉，张源凯，等.基于关联网络的机器人移动货架系统货位分配方法[J].工程管理科技前沿，2022，41（1）：56-64.

[14] 翟梦月，王征，李延通，等．可移动货架仓储系统中商品储位分配问题研究[J]．中国管理科学，2023，31（3）：167-176．

[15] 王征，鲁鹏，胡祥．可移动货架仓储系统中的货架位置优化方法[J/OL].中国管理科学：1-12.[2023-08-09]．http：//kns.cnki．   net/kcms/detail/11.2835.G3.20210908.1726.002.html．

[16] YUAN Rong，CEZIK T，GRAVES S C．Stowage decisions in multi-zone storage systems [J]．International Journal of Production Research，2018，56（1-2）：333-343．

[17] 李珍萍，范欣然，吴凌云．基于“货到人”拣选模式的储位分配问题研究[J]．运筹与管理，2020，29（2）：1-11．