跨学科视角下中考数学试题比较与分析

2024-06-19李婉瑜倪伟侠赵宏艳李佳汤获

赤峰学院学报·自然科学版 2024年5期

李婉瑜倪伟侠赵宏艳李佳汤获

摘要：在跨学科视角下，选取赤峰市2018—2023年中考数学试题为研究对象，从学科来源、题型、呈现方式、使用目的、知识领域等五个维度构建分析框架，对近6年赤峰市中考数学跨学科试题进行比较与分析，得出如下结论：跨学科试题的维度内容分布不均，跨学科试题的使用目的类型单一。基于上述结论，本文为中考数学命题者提出相应建议：均衡跨学科试题的维度内容分布，调整跨学科试题的使用目的类型。

关键词：跨学科；中考数学；试题分析

中图分类号：G633.6 文献标识码：A 文章编号：1673-260X（2024）05-0097-05

随着教学改革的不断深入，跨学科内容在教学过程中占据了重要地位，并以不同的形式在各种试题中出现。在数学学科中，跨学科内容的定义是将两门及以上不同学科的知识结合在一起的内容，从概念、原理、方法、思想的简单交流到深层次的相互联系[1]。《义务教育数学课程标准（2022年版）》（以下简称新课标）指出，要设立跨学科主题学习活动，加强学科间相互关联，带动课程综合化实施，强化实践性要求[2]。在中国知网以“跨学科试题”进行主题检索，共有67篇文献，涉及每个学科，如，蔡防琴分析高考历史（江苏卷）跨学科试题的命题趋势并提出了相对应的策略[3]；王刚统计归纳了2000—2011年的高考文综跨学科试题，总结了学生解题的思路[4]；刘兰英对2012—2019年通辽市中考化学试题的内容进行分析并提出教学建议[5]；杨凤娣以全国Ⅰ卷高考历史（除选考题）的跨学科试题为研究对象，对跨学科试题的分值、类型、材料进行分析并归纳其特点[6]。其中有22篇是对中高考数学跨学科试题的分析，如朱文彦对跨学科中考试题进行归类、举例和赏析[7]；朱广科将各地的中考跨学科试题分为九类，涉及各个学科，对其进行解析并提出跨学科试题的解题策略[8]；黄贤明根据跨学科内容的功能将试题分为三类：点缀呈现型、情境应用型和综合拓展型，总结数学跨学科试题的价值，提出相关的教学启示[9]；刘祖希从六个维度分析2022年全国高考数学试卷的跨学科试题，对数学跨学科内容与教学的研究提出展望[10]；倪方友评析2022年初中学业水平考试数学的跨学科试题，对其进行反思并提出意见：精选教材、精准结合和科学呈现[11]；陈泽宁对2010年部分省市的中考数学跨学科试题进行分类并举例说明[12]。仅有1篇是对中考数学跨学科试题的比较研究，黄凯等人研究了2017—2021年浙江省中考数学试题中的跨学科内容，对中考数学试题的编制提出意见[13]。基于上述分析，本文对赤峰市2018—2023年（以下简称近6年）中考数学跨学科试题进行比较分析，目的是了解赤峰市中考数学跨学科试题的变化趋势，为今后中考数学跨学科试题的编制提供一些建议。

1 研究对象与分析框架

1.1 研究对象

中考是义务教育阶段的终结性考试，也是高中入学的选拔性考试，对学生的德智体美劳等各方面进行综合性评价。为了更好地了解中考数学跨学科试题的变化趋势，本文以赤峰市近6年中考数学跨学科试题为研究对象，从不同的维度对其进行比较分析，为赤峰市中考数学跨学科试题的编制提供参考。

1.2 分析框架

本文在张维忠等人构建跨学科内容分析框架的基础上[13，14]，对赤峰市近6年中考数学试题进行统计分析，该分析框架从学科来源、题型、呈现方式、使用目的、知识领域等五个方面进行构建，如表1所示。

为了使中考数学跨学科试题的分析结果更具有客观性，在统计时，若试题中包含多个学科来源、使用目的和知识领域，则分别进行统计。例如，对学科来源而言，“利用测角仪、镜子、皮尺等工具和光的反射定律来测量校园内旗杆的高度”，则分别将工程与技术科学（测绘科学技术）和自然科学（物理学）相关系数都进行加“1”处理。对使用目的而言，“龟兔赛跑这则寓言故事所反映的大致运动图像”，则分别将提供背景性情境和提供应用性情境相关个数都进行加“1”处理。对知识领域而言，“建立模型求学校水池的面积”，则分别将数与代数和综合与实践活动相关个数都进行加“1”处理。

2 比较结果与分析

2.1 跨学科试题的学科来源分析

赤峰市每年中考数学试题都是26道，六年共计156道。2018—2023年跨学科试题分别为6道、7道、8道、9道、11和10道，共计51道，整体呈现上升的趋势。其中，2022年跨学科试题的数量最多，有11道，占试题总量的42.31%，这说明了中考数学命题者对新课标中的跨学科内容关注度较高。

近6年赤峰市中考数学试题的跨学科内容涉及每个学科，但关于农业科学和医药科学的跨学科试题较少。其中，人文与社会科学试题最多，有28道，占跨学科试题总量的50.9%，主要涉猎哲学、体育科学、经济学、社会学等领域，如射击运动成绩的方差分析、篮球比赛的方程问题、运动路程等。工程与技术科学试题有13道，占23.64%，主要涉猎电子与通信技术和测绘科学技术领域，如无人机测量楼房高度的问题，这侧面反映了中考试题命题的与时俱进，与现代科学技术紧密联系，让学生在试题中体会到“数学来源于生活”的思想。自然科学试题占跨学科试题总量的20%，主要结合物理学和天文学的相关知识来考查科学计数法的知识点，如北斗导航卫星的授时精度、液体压强与深度的关系。最后，来源于农业科学和医药科学的跨学科试题较少，分别出现2道和1道。关于农业科学的跨学科试题在2018—2021年均没有出现，仅在2022年和2023年各有1道题，主要涉猎林学和农学两个领域，考查统计与概率和数与代数的相关知识点。关于工程与技术科学的跨学科试题题数在2020年和2022年得到增加，题数均为4道，其余年份题数均为1～2道。

2.2 跨学科试题的题型分析

近6年赤峰市中考数学跨学科试题以选择题居多，共有24题，占比47.06%；填空题和解答题分别占19.61%和33.33%，相差不大。2018年跨学科试题仅以选择题和解答题的形式出现，没有出现填空题。2019年和2020年的跨学科内容在各种题型中分布大致相同。2021年和2022年的跨学科试题主要以选择题的形式出现，填空题和解答题相对较少。2023年的跨学科试题主要以选择题和解答题的形式，填空题仅有1道出现。以填空题的形式呈现的跨学科试题，在2018年没有出现，在2019—2023年均有1～3道的跨学科试题出现在填空题中，实现了新的突破，使题型分布更加合理。因此，今后中考数学命题者不仅要编制新颖的跨学科试题，还要注意跨学科试题在各种题型中的分布情况。

2.3 跨学科试题的呈现方式分析

近6年赤峰市中考数学跨学科试题的呈现方式主要是图文并茂，共有34题，占比66.67%，如表2所示。通过几何图、统计表、示意图等形式并结合文字语言来编制跨学科试题，更有利于学生清晰地理解题意和解决问题。文字描述占比33.33%，每年的题数分布均匀，而没有涉及装饰类型插图。这说明中考数学试题的命题内容都与考查的知识点有关，不会为了装饰试题出现与数学试题无关的图景图片，试题编制具有严谨性。2018和2019年以图文并茂呈现的跨学科试题最少，每年仅有4道题，在2022年和2023年才增加以图文并茂呈现的跨学科试题题数。以文字描述呈现的跨学科试题每年的题目变化不大，均为2～3道题。

跨学科试题在三种题型中呈现方式的具体表现为：选择题以文字描述和图文并茂方式呈现，都是12道，均匀分布。填空题仅以图文并茂方式呈现，较为单一。解答题主要以图文并茂方式呈现，目的是降低学生应用跨学科知识解题的难度。

2.4 跨学科试题的使用目的分析

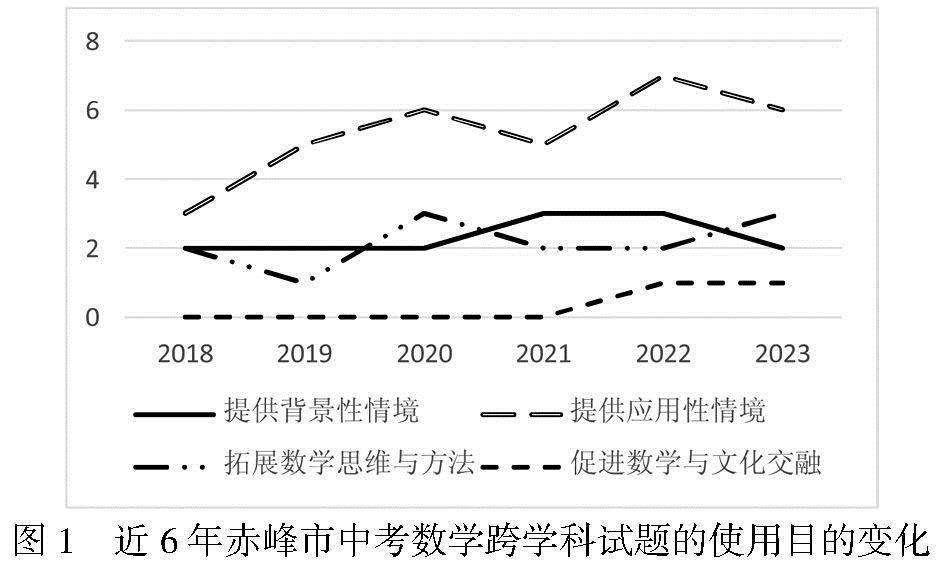
结合唐恒钧等学者构建的数学到文化实践之间的价值连续系统[15]，将使用目的分为4个维度，如图1所示。

跨学科内容的设置仅为了给学生提供熟悉的情境，让学生能够通过情境问题来挖掘隐含的数学条件，进而运用所学的数学知识来解决问题。在近6年的跨学科试题中，每年关于使用目的为提供应用性情境的试题出现得最多，均有4～7题。2018—2023年使用目的中提供背景性情境呈相对稳定状态，主要涉及体育学科、电子与通信技术、社会学、测绘科学技术和哲学这五个学科。2018—2023年使用目的中提供应用性情境整体呈上升趋势，主要涉及经济学、交通运输工程和物理学这三个学科。拓展数学思维与方法的试题题数变化较为曲折，以物理学和经济学为主，这说明了理工科之间紧密联系，注重拓展学生的数学思维与方法，同时与理工科相结合的跨学科试题会加大试卷难度，这对学生综合运用各科知识的能力有一定的要求。使用目的中促进数学与文化交融的试题仅在2022年和2023年分别出现1道，试题中融入赤峰红山文化和非物质文化遗产代表作剪纸艺术，目的是增加学生对地方历史文化和中华传统文化的了解。因此，在中考试题的编制中应多融入地方文化和传统文化的色彩。

2.5 跨学科试题的知识领域分析

根据新课标将初中数学课程内容划分为四个知识领域进行分析。近6年赤峰市中考数学跨学科试题在这四个领域的占比大致相同，即数与代数和图形与几何，分别占比26.56%和29.69%，统计与概率和综合与实践，分别占比23.44%和20.31%。在图形与几何这一知识领域中，有关跨学科的内容试题每年都呈现上涨的趋势，其他知识领域的变化趋势较为稳定。可见，近6年赤峰市中考数学试题的知识领域分布较为均衡，每个领域的知识点都考查，试题的编制内容是严谨合理的，有利于考试的公平合理。

图形与几何的知识点常以选择题或填空题的形式出现，通常考查跨学科知识背景下的函数图像变化。在数与代数的知识考查中，跨学科常以其他学科知识为背景和应用情境来考查相关数学内容，借助其他学科知识来增加数学试题的丰富度。体育学和艺术学的跨学科内容常为统计与概率的知识点提供背景情境，题目情境的熟悉度能降低学生解题的难度。在综合与实践这一知识领域，常结合经济学、交通运输工程等跨学科内容创设问题情境，通过设置问题链的形式来检验学生的学习成果。

3 结论与建议

3.1 结论

基于跨学科的视角，对赤峰市近6年中考数学试题进行比较分析，得出如下结论。（1）跨学科试题的维度内容分布不均。如学科来源中人文与社会科学占50.9%，医药科学仅占1.82%；题型中选择题占47.06%，填空题占19.61%；呈现方式中图文并茂占66.67%，但没有出现装饰类型插图。（2）跨学科试题的使用目的类型单一。如使用目的中提供应用性情境的试题较多，有32道，主要涉及经济学、交通运输工程和物理学这三个学科，而使用目的中促进数学与文化交融的试题仅有2道，在试题中融入红山文化和剪纸艺术传统文化。

3.2 建议

通过对近6年赤峰市中考数学跨学科试题变化趋势的比较分析，笔者对中考数学命题者提出建议。（1）均衡跨学科试题的维度内容分布。在学科来源中，中考试题命题者要均衡不同学科内容在试题中的分布情况，进一步扩大跨学科试题选材的范围。例如，医药科学中有关的药物药效、疾病预防等问题可以和统计与概率相结合；农业科学中有关植物的生长情况、动物的繁殖速度等可以和函数相结合。在今后的试题编制中，可以融入上述材料，这样能够均衡试卷中跨学科的内容，可以让学生体会到数学与各个学科之间的密切联系。在题型分布和呈现方式中，中考试题命题者要均衡跨学科内容在试卷中的题型分布情况和呈现方式，进一步拓展跨学科内容的深度和广度。例如，多设置有关跨学科内容的填空题和解答题，编制题目时也可采用除文字描述和图文并茂以外的形式。在今后的试题编制中，多注意跨学科内容在试题中的题型分布和呈现方式，增加试题编制的合理性。（2）调整跨学科试题的使用目的类型。在使用目的中，中考试题命题者要创设新颖又有深度的题目，调整跨学科试题使用目的的类型。跨学科试题不单为其提供背景和应用情景，还可以与其他学科知识相结合，打破学科间的壁垒，拓展学生的数学思维与方法，并融入不同的文化历史，促进数学与文化融合，增加跨学科试题使用目的的类型。例如，可以将冬奥运动员事例、航天航空知识、HPV疫苗效果等社会热点融入试题中，将社会时事中的跨学科内容与数学相结合进行编制题目，能更好地体现数学的应用价值。与此同时，中考试题命题者要结合跨学科内容，合理选择课本的数学知识点来进行编制题目。例如，生态文明的建设、乡村振兴的建设等可以和综合与实践的知识点相结合，疫苗的防疫效果、人口普查问题等可以和统计与概率的知识点相结合。跨学科试题的编制要源于课本，又高于课本，合理选择知识点，编制综合领域的跨学科交叉试题，提高试卷的综合性与全面性，更有利于全能型人才的选拔。

参考文献：

〔1〕尚念.中美初中数学教材跨学科内容的比较研究[D].上海：华东师范大学，2017.

〔2〕教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学版社，2022.

〔3〕蔡防琴.高考历史命题中的跨学科趋势及应对策略[D].扬州：扬州大学，2017.

〔4〕王刚.近十二年高考文综跨学科试题统计分析[J].中学地理教学参考，2012，41（Z1）：4-29.

〔5〕刘兰英.通辽市中考化学有关跨学科试题的内容分析与教学建议[D].呼和浩特：内蒙古师范大学，2020.

〔6〕杨风娣.高考历史跨学科试题研究及教学启示[D].南昌：江西师范大学，2022.

〔7〕朱文彦.跨学科的中考数学题型[J].数学教学通讯，2002，24（02）：23-24.

〔8〕朱广科.中考数学跨学科试题归类解析[J].教学与管理，2012，29（04）：62-64.

〔9〕黄贤明.数学跨学科试题研究——兼及教学启示[J].教育研究与评论（中学教育教学），2023，15（05）：27-31.

〔10〕刘祖希.关于数学跨学科内容与教学的已有研究——兼及2022年全国高考数学试卷跨学科试题分析[J].教育研究与评论（中学教育教学），2022，14（12）：5-11.

〔11〕倪方友.指向学科素养凸显育人价值——2022年初中学业水平考试数学跨学科类试题评析与反思[J].中小学数学（初中版），2023，41（03）：37-39.