超临界二氧化碳系统用箔片气体动压轴承静特性研究

朱鹏程 管玉坤 门日秀 程振宇 冯凯

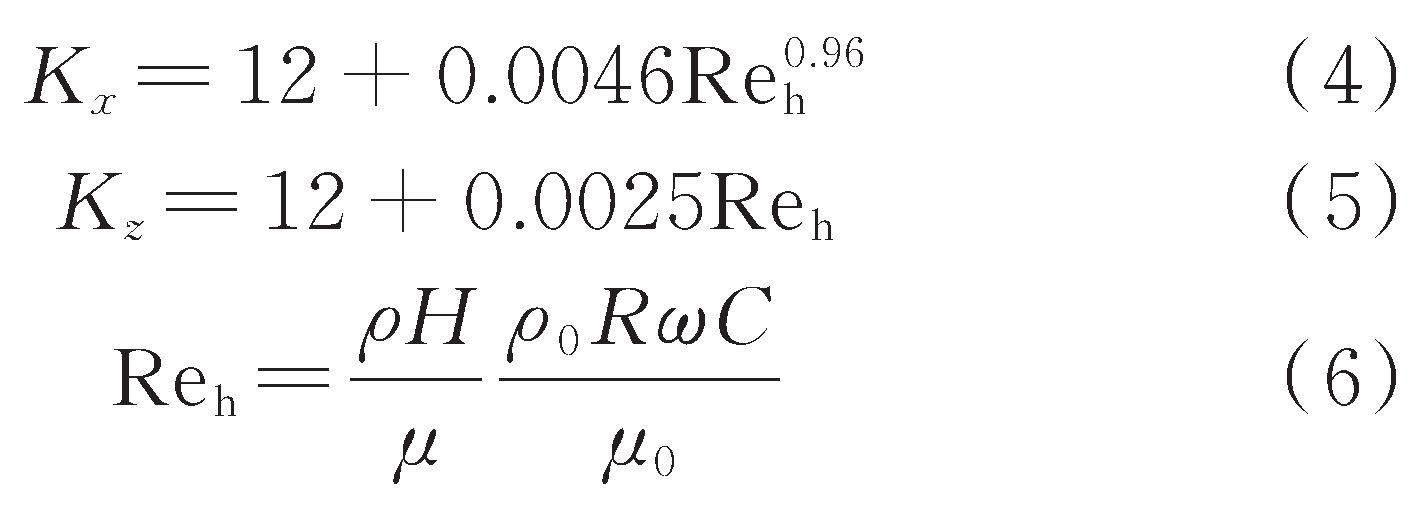
摘要： 超临界二氧化碳动力循环系统对实现节能减排的目标有着十分积极的作用。针对一种箔片气体动压轴承结构建立了计算模型，并通过拟合非理想状态气体超临界二氧化碳的密度与压力之间的关系，基于传热学模型和气体润滑能量方程分析了轴承气膜温升，结合实际运行过程中出现的湍流效应修正润滑气体雷诺方程、耦合力学分析模型和能量方程，分析S?CO2介质箔片气体动压轴承的静特性，并与空气作为介质进行对比分析不同系统参数和湍流参数对轴承特性的影响规律。结果表明：相较于空气而言，使用超临界二氧化碳作为润滑介质的箔片气体动压轴承具有较高的承载力，而且在一定范围内随着轴承直径和宽度的增加、偏心率的上升、轴承间隙的减小、转速的提高等，轴承承载力均可以增大；对于湍流影响因素来说，在一定范围内随着局部雷诺数和湍流系数的增加、气体动力黏度和密度的提高、高温环境下环境温度的降低等，轴承承载力将会增大。

关键词： 箔片气体动压轴承； 雷诺方程； 超临界二氧化碳； 承载力

中图分类号： TH133.37； O347.6    文献标志码： A    文章编号： 1004-4523（2024）05-0875-10

DOI：10.16385/j.cnki.issn.1004-4523.2024.05.016

引  言

基于超临界二氧化碳（S?CO2）介质实现热功转换的动力循环装置具有能量密度高、结构简洁紧凑和洁净度高等特点，因此，广泛应用S?CO2动力循环系统对实现节能减排的目标有着十分积极的作用［1］。但是由于S?CO2动力装置对其中的旋转机械具有宽温域、超高压、超高转速、结构紧凑等要求，传统的转子?轴承系统将面临润滑失效、轴系失稳和发热严重等问题［2］。具体来说，传统润滑滚动轴承和滑动轴承的转速相对较低，油润滑轴承还会受到其结构形式、润滑油特性、供油管路的影响，这致使轴承尺寸较大，在较高或较低温度下性能较差，并导致旋转机械在小尺寸、宽温域、高转速领域的广泛应用受限，因此传统油润滑轴承无法满足S?CO2旋转机械轴系支撑的要求［3］。为了克服传统油润滑轴承存在的上述不足，实现旋转机械应用于S?CO2动力循环系统的目标，直接依靠气体润滑的箔片气体动压轴承技术在S?CO2旋转机械中得到了初步应用，其具有无油、免维护、高转速、系统简单等优点，是S?CO2旋转机械轴系理想的支承装置［4］。

波箔型径向箔片气体动压轴承由轴承套、波箔和顶箔构成。当转子高速旋转超过其起飞转速后，转子和箔片之间的气体可以通过楔形效应形成的高压气膜将转子悬浮在轴承中，而无需供气、供油管路，这极大地缩减了旋转机械的重量、体积和成本；同时由于箔片气体动压轴承使用气体作为润滑介质，可以避开润滑油在高温或低温状态下的润滑失效，因此箔片气体动压轴承具有在宽温域下工作的能力［5］。综上所述，使用箔片气体动压轴承支承的转子系统具有超高转速、高效率、长寿命、免维护、强环境适应等优点［6］，在现代高速旋转机械中应用广泛。

为了耦合超临界二氧化碳介质独有的物性特点和箔片气体动压轴承的运行特性，Conboy［7］针对 S?CO2 润滑的轴承进行建模，在原有理想气体可压缩雷诺方程的基础上加入了湍流修正系数来计算轴承的静态特性，给出了湍流状态下轴承特性随环境压力的变化，验证了关于 CO2 轴承中湍流效应占主导地位的假设，不足的是此研究中将S?CO2视为理想气体，而事实上S?CO2气体与理想气体的特性差别较大； Kim［8］采用了修正的雷诺方程，进行了径向箔片气体动压轴承的三维热流体动力学分析，考虑了气膜内部的湍流效应； Qin等［9］使用昆士兰大学自主研发的流体动力学求解器 Eilmer 对润滑流体层进行仿真，该求解器考虑了流体的流动状态，且基于均质各向同性的 Kirchhoff方程模拟箔片的变形，使用该流固耦合模型研究 S?CO2 循环中推力轴承的弹流耦合现象，还发现了S?CO2介质中离心惯性力影响箔片气体动压轴承性能的机制；温建全［10］将 S?CO2 视为非理想气体，考虑了S?CO2气体密度和黏度随压力的变化，推导出考虑湍流效应的气体动压雷诺方程，并求解出S?CO2润滑的气体动压轴承静/动态特性；李卓聪等［11］基于ANSYS 和CFX软件，针对S?CO2润滑的动压轴承的动态特性开展了数值研究，获得了运行参数对轴承动态性能的影响规律。

目前，箔片气体动压轴承的润滑介质主要为常温常压下的空气，其主要的应用场合局限于高转速、高功率密度的空气压缩机、循环机、燃气轮机和电机中，鲜有针对基于S?CO2润滑介质的箔片气体动压轴承的研究，这制约了箔片气体动压轴承在S?CO2动力循环系统中的应用。不仅如此，现有研究大多数使用仅考虑层流的基于理想气体假设的气体润滑雷诺方程对轴承特性进行求解。因此，本文在一种箔片气体动压轴承的基础上，提出其力学分析模型，引入超临界二氧化碳作为润滑介质，考虑轴承在实际运行过程中出现的湍流效应和S?CO2气体的非理想气体特性，修正经典气体润滑雷诺方程，建立轴承静态特性弹流耦合数值计算方法，并分析不同系统参数对轴承的特性的影响规律，以期为箔片气体动压轴承在S?CO2动力循环系统中的应用提供理论基础。

1 理论模型

1.1 箔片轴承力学模型

搭接顶箔式波箔型气体动压径向轴承（Multi?leaf Foil Bearing， MLFB）是一种以气体作为润滑剂的自作用式气体轴承。通过环境介质气体的黏性、轴颈与顶箔表面相对运动时产生的动压气膜来支承转子系统。其结构如图1所示，它由轴承套、相互搭接的五瓣顶箔和五瓣波箔组成，顶箔与波箔的一端通过特殊定制的销钉被固定在轴承壳体上，另一端自由悬挂，顶箔表面镀有特氟龙镀层，因此较为光滑；同时箔片可以为轴承提供适当的刚度与阻尼。

综合考虑顶箔与波箔之间的摩擦、波箔与轴承套之间的摩擦、波与波之间的相互作用以及顶箔凹陷变形等多个因素，建立了完整的波箔弹性结构理论分析模型。将每个波箔结构单元简化为两个刚性杆和一个水平放置的线性弹簧，相邻单元的线性弹簧之间通过一个刚性连杆连接。连杆与连杆之间在波箔顶部采用铰链进行连接，且可以自由转动，如图2所示。图中F表示气膜压力。

波箔与波箔之间的相互作用力通过位于底部的刚性连杆进行传递。如果波箔发生弹性变形，则接触面之间会产生摩擦力和相对移动。由于连杆是刚性的，波箔的竖直变形量与弹簧水平变形量之间的几何关系如图3所示。图3中，为波箔半径，为半波角度，为等效连杆长度，为等效连杆与水平方向夹角。

波箔的竖直变形量与弹簧水平变形量之间的关系可以表示为：

式中。

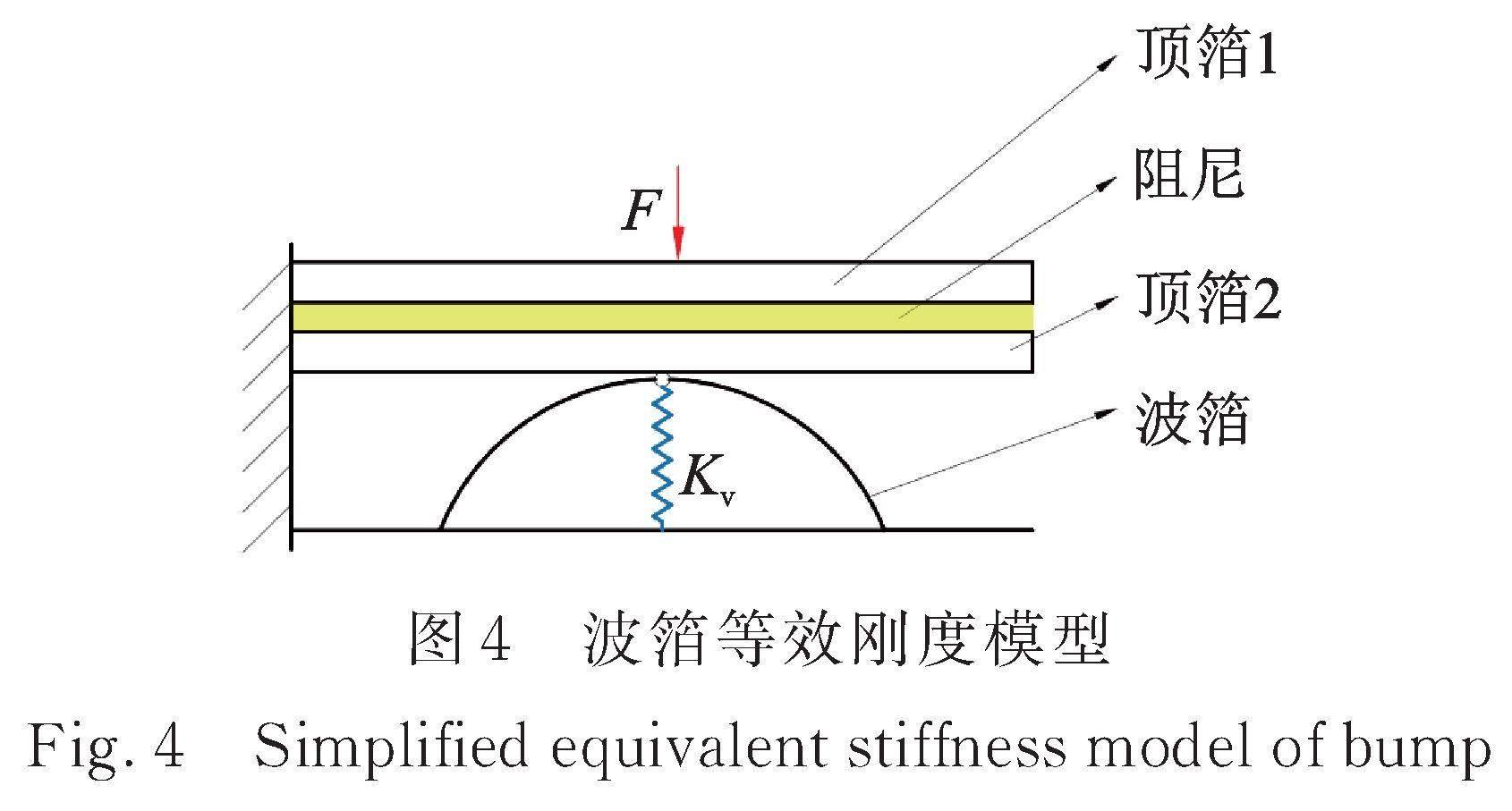
将弹性波箔结构单元等效为一个竖直方向的弹簧（如图4所示），该等效垂直刚度定义为。结合顶箔对波箔的影响，由于箔片极薄，因此对波箔进行简化的受力分析（如图5所示），可求得单个波箔的等效垂直刚度［5］为：

图5中，为水平等效连杆受力，为波箔与轴承套的摩擦力，为作用在波箔顶部的竖向力，和分别表示向右、向左的轴向力，为水平等效弹簧弹力［5］。

根据文献［12］的结论，结合实验数据及设计经验可以得知，搭接式顶箔结构在刚度方面相较于普通单顶箔?波箔结构不会有太大差距。因此将搭接式顶箔考虑成一块较厚的顶箔，以方便建立其刚度矩阵。简化后顶箔的厚度仍然极小，因此可以简化为三维的有限梁单元模型。该模型能有效模拟由于气膜压力分布不均而导致的顶箔薄膜凹陷变形。根据虚功原理，节点的变形量可以通过直接刚度法计算。将有限元法计算得到的顶箔等效刚度和每个波箔的等效垂直刚度在相连接的网格节点处相加，即可得到波箔和顶箔并联模型的等效刚度：

（3）

1.2 超临界二氧化碳介质润滑模型

为获得湍流润滑系数，Chung等［13］将考虑湍流效应的“壁面定律”用于分析湍流润滑，并假定湍流动量输运时存在各向同性特性，获得了湍流润滑系数的倒数和与局部雷诺数的关系曲线。基于此关系曲线，部分学者提出了非线性拟合关系式，经验证可以使用，但在将湍流润滑系数代入雷诺方程求解时会较为复杂。为简化雷诺方程的求解过程，本文通过非线性和线性拟合获得湍流润滑系数与局部雷诺数之间的关系如下式所示：

式中为润滑气体密度；为润滑气体初始密度；为气膜厚度；为润滑气体黏度；为润滑气体初始黏度；为转速；为轴承名义间隙。

在仅考虑湍流的可压缩气体雷诺方程中加入湍流修正系数，并选取相应的无量纲参数后，可以得到变黏度变密度的稳态湍流雷诺方程如下式所示：

多数学者在求解雷诺方程时会将介质看成理想状态气体，因此可以根据理想气体状态方程将雷诺方程中的密度直接替换为压力，同时将动力黏度考虑成常数，这种做法虽可以极大地简化求解过程，但是在S?CO2润滑介质中显得有失妥当，因为事实上此时的润滑气体S?CO2已经严重偏离理想气体的范畴，且动力黏度也会随着温度的变化而发生改变。因此本文首先基于物性数据库导出CO2气体在超临界区域的物性，并通过建立S?CO2气体在不同的温度环境下密度与压力之间的关系，将雷诺方程中的密度用压力进行表达。此时动力黏度既是温度也是压力的非线性函数，但为了计算简便，本文忽略了黏度随压力的变化，将黏度考虑为温度的函数。根据泰勒定理，无量纲密度与压力之间的关系可以用带皮亚诺余项的泰勒公式表达：

（8）

化简式（8），并略去高阶无穷小量，可以得到：

（9）

将式（9）代入雷诺方程式（7），同时引入如下中心差分公式：

通过式（10）和（11）即可求解出气膜压力、气膜厚度和轴承其他静态参数。

1.3 考虑气膜能量方程的温度模型

润滑气体能量方程［14］为：

式中为比热容；分别代表周向、径向和轴向方向；分别为周向、径向和轴向的气体流速；T为气膜温度。

气膜温度传导的方向主要沿径向，因此轴向和周向的温度梯度非常小。因此，对能量方程进行化简，得到黏温方程：

（15）

将式（15）代入式（14），并进行无量纲化，得到：

其中：

气膜传热的边界条件如图6所示。

箔片气体动压轴承中润滑气膜径向厚度方向的内侧表面与转子外表面接触，外侧表面与顶箔内表面接触，同时气膜温度在入口处与进气温度相同，如图6所示，则能量方程在气膜入口处、转子外表面和顶箔内表面处的温度边界条件为：

式中为进气口温度（K）；为转子外表面温度（K）；为顶箔内表面温度（K）。

气膜在顶箔固定点前缘入口处的温度可由轴承吸入的冷却气流和轴承中循环气流的气体混合能量平衡关系式得到。实际过程中气体比热容变化不大，气膜入口处温度可表示为［15］：

式中  Qrec和Trec为循环气体的流量（m3/min）和温度（K）；Qsuc和Tsuc为吸入气体的流量（m3/min）和温度（K）。

气膜中一部分热量通过顶箔1传导至顶箔1和顶箔2接触平面，进而热量继续传导至顶箔2另一平面，在这个平面上，由于顶箔2与波箔实体的接触部分属于线接触，接触面积相对较小，因此此时热量绝大多数将通过空气对流传热以及通过热辐射传递至波箔上平面，继而热量在波箔实体上通过热传导传递至波箔下平面，此时波箔实体与轴承套非直接接触的部分充满介质气体，因此波箔下平面的热量还会通过热辐射、对流换热传递至轴承套上，轴承套上的热量最终通过对流传热和辐射传热扩散到周围环境中。根据上述传热路径，建立热阻模型如图7和8所示。其中，Tg?t为顶箔侧气膜温度，Tamb为环境温度RZCT表示轴承套的热阻，Tg?s为转子侧气膜温度，气膜中另外一部分热量则通过轴颈的热传导输送至轴颈空心内壁上，随后经对流传热和热辐射传导至介质气体中。各热阻参数的计算公式及物理意义如表1所示。

箔片结构总热阻的计算公式为：

当轴承温度达到稳定状态时，从气膜传递到顶箔中的热量和从顶箔传递出去的热量将处于动态平衡状态。建立如下热平衡方程：

2 数值模拟计算方法

径向轴承静态特性数值求解流程如图9所示。其中δ0为泊片初始变形。首先基于湍流雷诺方程求解气膜的压力分布，随后使用Link?Spring模型和有限元梁模型求解箔片的变形，两者在Matlab中耦合。在每一次的迭代计算中，都需要通过湍流雷诺方程求解出气膜压力分布，并基于Link?Spring模型进行受力分析，计算出波箔的等效垂直刚度矩阵，并将其添加到顶箔的刚度矩阵中，从而获得支承结构的总刚度。随后基于简化的气膜能量方程求解出气膜平均温升，并根据温度来获得新的动力黏度数值、新的系数矩阵K，将求得的箔片变形应用于下一步气膜压力分布的迭代计算。当前后两次迭代求解的气压分布和箔片变形的差值均小于其数值的万分之一时，迭代求解结束，输出此时的气膜压力分布、气膜厚度、温升和箔片变形等。计算的初始参数为：轴承内径为45 mm、宽度为60 mm、名义间隙为0.07 mm，环境压力为7 MPa，环境温度为400 K。

3 计算结果及分析

3.1 承载力计算结果及对比分析

图10是在不同偏心率下基于超临界二氧化碳介质的轴承承载力随转速的变化结果图。从图10中可以看出，随着轴承偏心率的上升，不同转速下的S?CO2箔片气体动压轴承承载能力均有显著上升，此结果与使用常温常压空气作为润滑介质的相同轴承的静态特性较为类似。从图10中还可以看出，在偏心率达到0.9、转速为70 kr/min时，使用S?CO2介质进行润滑的箔片气体动压轴承的承载力甚至超过了700 N。

与空气作为润滑介质相对比，当偏心率分别为0.5，0.75和0.83时，不同介质、不同转速下的箔片气体动压轴承承载力对比分析如图11所示。从图11中可以看出，使用S?CO2作为润滑介质的气体轴承相比传统空气轴承的承载力有所提升；在偏心率和转速较低时（如e=0.5，转速小于40 kr/min），轴承承载力的提升并不明显；但当偏心率较大、转速也较高时（如e=0.75，转速为50 kr/min），轴承的承载能力呈现成倍增加的趋势。不仅如此，随着偏心率和转速的进一步加大，处于两种不同介质的箔片气体动压轴承的承载力差距进一步扩大，且相比传统空气润滑介质而言，使用S?CO2进行润滑的气体轴承在转速提高时承载能力提升得更为迅速。

图12是箔片气体动压轴承在常温常压空气介质和S?CO2介质下的气膜压力分布情况。从图12中可以看出，S?CO2介质和常温常压空气介质的箔片气体动压轴承在相同轴承参数、同样外载荷（100 N）情况下的压力分布规律和变化趋势基本相同；还可以看出，在S?CO2介质下，气体轴承处于高环境压力（7 MPa）状态，因此其无量纲相对压力在图中显得相对较小。

图13是气体轴承在常温常压空气介质和S?CO2介质下的气膜厚度分布情况。从图13中可以看出，二者在相同载荷（100 N）下厚度分布规律较为相似，但是气膜厚度变化规律却有较大不同。可以看出，从第0个有限元结点到最小气膜厚度位置，S?CO2介质下的气体轴承气膜厚度的下降速度比常温常压空气介质下的气膜厚度的下降速度要快；在同等载荷的作用下，S?CO2介质下的气膜厚度比常温常压空气介质下的厚度要大，这是因为前者的气膜不需要达到相对很高的刚度就足以支撑外界载荷，因此其气膜厚度相对于后者来说还有很大的进一步缩小的潜力，因此前者还能继续为外载荷提供更大的支撑刚度，即前者形成的高压气膜的承载能力将会大于后者。

3.2 轴承结构参数对轴承静特性的影响

图14是轴承静态承载能力随不同轴承半径、不同轴承宽度和不同偏心率的变化规律。从图14中可以看出，在轴承半径增大的情况下，轴承静态承载能力获得了较为明显的增大；增大轴承宽度也会致使轴承承载力增大；在大偏心率下，轴承的承载力随着半径和宽度的变大而显著增大，这是因为箔片气体动压轴承在偏心率达到“动压区”后，承载力会显著增大，文献［6］的研究结论中也有类似现象。

图15是轴承静态承载能力在不同偏心率、不同名义间隙下的变化规律。从图15中可以看出，在名义间隙减小的情况下，轴承的承载力获得了较大的提升，且在大偏心率的情况下，轴承的承载能力增大得更为明显，这是因为名义间隙对气体轴承的初始气膜厚度的影响很大，而初始气膜厚度较大时，气膜的刚度会有所下降，进一步影响到气体轴承的承载力，但是过大地减小轴承名义间隙也可能会导致气体轴承起飞后磨损严重、发热功率高，甚至根本无法正常起飞等问题。因此在一定范围内，适当地减小箔片气体动压轴承的名义间隙可以获得比较大的承载能力，文献［16］的研究结论中也有类似现象。

3.3 环境介质参数对轴承静特性的影响

图16是轴承静态承载能力在不同偏心率、不同局部雷诺数下的变化规律。从图16中可以看出，在偏心率增大和局部雷诺数增大的情况下，箔片气体动压轴承的承载力将会不断增大，其原因可以从雷诺方程和实际情况两方面来解释。从雷诺方程来看，局部雷诺数的增大会直接影响到湍流系数并致使其湍流系数变大，因而雷诺方程中作为分母的湍流系数和局部雷诺数会进一步增大方程中的气膜相对压力，进而提高处于湍流状态气体轴承的承载力；对实际情况进行分析，当气体雷诺数增大后，其气体密度增大，这对气膜内压力值和轴承承载力具有不可忽略的影响，特别是在一定范围内，环境气体密度的增大可以提升其因动压效应产生的高压气膜的静态刚度，因此可以提升箔片气体动压轴承的承载力，文献［10］的研究结论中也有类似现象。

图17是轴承静态承载能力在不同偏心率、不同湍流系数下的变化规律。从图17中可以看出，在偏心率增大和湍流系数增大的情况下，轴承的承载力一直在增大，其原因可以从雷诺方程和实际情况两方面来解释。从雷诺方程来看，作为分母出现的湍流系数是局部雷诺数的正相关函数，因此其湍流系数对轴承承载力的影响和原因这里不再赘述。从实际情况来看，环境气体中出现的湍流效应可以极大地增加气膜流动时的摩擦阻力，而湍流系数则是湍流效应的量度，因此轴承的阻尼和承载力均会相应增大，但是湍流效应过强则会导致气体轴承起飞后发热功率过高的问题，发热量过大甚至可能会损坏轴承中的箔片高温涂层等关键部件，因此在一定范围内增大湍流系数可以使得气体轴承获得更好的阻尼和承载力。

图18是箔片气体动压轴承静态承载能力在不同偏心率、不同环境压力下的变化规律。从图18中可以看出，随着环境压力的上升，轴承的承载力在逐步提升。从雷诺方程来看，环境压力的提高会影响超临界二氧化碳介质气体的密度，进一步影响到介质气体的雷诺数，进而对轴承的承载力产生影响。不仅如此，大幅度环境压力的改变还会在一定程度上影响气体的其他物性，如气体动力黏度和传热系数等，以至于会对轴承静态特性产生不可忽略的影响。因此不考虑其他因素的影响，在一定范围内适当提高环境压力，可以增大箔片气体动压轴承的承载能力。

图19是箔片气体动压轴承静态承载能力在不同偏心率、不同动力黏度下的变化规律。从图19中可以很明显地看出，在对动力黏度进行极其微小的调整后，承载力的变化不容小觑，且承载力随着动力黏度和偏心率的增大而增大，这是因为二氧化碳气体在超临界态下的黏度远比常温常压的空气大，大黏度可以获得更好的阻尼特性和承载能力，但在理论上也会相应地提高轴承发热功率，因此在一定范围内适当地提高黏度能增加超临界二氧化碳介质箔片气体动压轴承的承载力。图20是箔片气体动压轴承静态承载能力在不同偏心率、不同环境温度下的变化规律。从图20中可以看出，随着环境温度的升高，气体轴承的承载能力逐渐下降。从雷诺方程来看，环境温度的升高会影响超临界二氧化碳介质气体的压力与密度之间的关系，进一步影响到雷诺方程中的无量纲气膜压力大小，基于此影响到整个迭代求解算法。不仅如此，环境温度的升高还会影响到介质气体的黏度和密度。因此在环境温度升高的过程中，超临界二氧化碳介质箔片气体动压轴承的承载力会随着黏度和密度的下降而呈现轻微降低的趋势。

4 结  论

本文在改进了箔片气体动压轴承力学分析模型的基础上，引入S?CO2作为润滑介质，考虑湍流效应和非理想气体特性，修正

Li Zhuocong， Li Zhigang， Li Jun. Investigation on the dynamic characteristics of gas foil thrust bearings for supercritical carbon dioxide（S-CO2） cycles［J］. Journal of Engineering Thermophysics， 2020， 41（12）： 2964-2969.

［12］赵晓荣. 多叶波箔型气体动压轴承静特性及气动加热数值研究［D］. 南京： 南京航空航天大学， 2016.

Zhao Xiaorong. Numerical research on the static and  aerodynamic heating characteristics of  multi-leaf compliant foil bearings［D］. Nanjing： Nanjing University of Aeronautics and Astronautics，2016.

［13］Ng C W， Pan C H T. A linearized turbulent lubrication theory［J］. Journal of Basic Engineering， Transactions of the ASME， 1965， 87（3）： 675-688.

［14］Peng Z C， Khonsari M M. A thermohydrodynamic analysis of foil journal bearings［J］. Journal of Tribology， 2006，128（3）： 534-541.

［15］Zhang K， Zhao X Y， Feng K， et al. Thermohydrodynamic analysis and thermal management of hybrid bump?metal mesh foil bearings： experimental tests and theoretical predictions［J］. International Journal of Thermal Sciences， 2018， 127： 91-104.

［16］赵雪源. 新型高阻尼气体箔片轴承及其转子系统的理论和实验研究［D］. 长沙： 湖南大学， 2017.

Zhao Xueyuan. Theoretical analysis and experimental investigation on the performance of a novel gas foil bearing with high structural damping and its rotordynamic response［D］. Changsha： Hunan University， 2017.

Static characteristics of gas foil bearing for supercritical carbon dioxide system

Abstract： The supercritical carbon dioxide power cycle system has a very positive effect on the realization of energy saving and emission reduction goals. In this paper， a calculation model is proposed for a foil gas dynamic pressure bearing structure. By fitting the non-ideal state gas supercritical carbon dioxide， the relationship between density and pressure is established. Based on the heat transfer model and the gas lubrication energy equation， the temperature rise of the bearing gas film is analyzed.  The Reynolds equation of the lubricating gas is corrected in combination with the turbulent effect in the actual operation process， coupled with the mechanical analysis model， Reynolds equation and energy equations， the static characteristics of foil gas dynamic pressure bearings are analyzed， and compared with air as a medium to analyze the influence of different system parameters and turbulence parameters on the bearing characteristics. The results show that compared with air， the foil gas dynamic pressure bearing using supercritical carbon dioxide as the lubricating gas has a higher bearing capacity， and within a certain range， the bearing capacity can increase with the increase of bearing diameter and width， eccentricity， the rotational speed and the reduction of the bearing clearance. For the turbulent influencing factors， within a certain range， the bearing capacity can increase with the increase of the local Reynolds number and turbulence coefficient， aerodynamic viscosity， density for ambient gas and the decrease of ambient temperature.

Key words： gas foil bearing；Reynolds equation；supercritical carbon dioxide；bearing capacity