考虑实测信息的既有规则建筑状态识别与抗震性能快速评估

单伽锃 周子杰 王律己 余桦 苏金蓉

摘要： 城市既有建筑（群）的地震安全性评价面临高效分析、快速评估、定量判定的多重技术发展需求。考虑长期服役过程中的结构性能演化现象，既有建筑安全性评价需要结构本身和当地地震动等一系列实测数据与信息，以标定结构真实服役状态，保证结构抗震性能评估结果的准确性，并兼顾结构抗震性能分析的时效性。本文基于等效非线性单自由度模型，结合作者近年来在数据驱动型状态评估指标方面的研究成果，提出了以既有建筑实测模态频率和阻尼比映射结构宏观服役状态，结合当地实测地震动数据集，快速评估该目标建筑抗震安全性的方法。阐述了基于动力测试和HAZUS技术手册的既有结构等效非线性单自由度模型的建立过程，提出了两类结构状态评价指标，结合多元工程性能参数，建立了等效模型变形状态与不同抗震性能水准之间的直接联系。以四川省珙县当地一栋高层规则框架结构和2019至2022年间10次实测地震动为例，对该建筑在当地近期实际地震动作用下的抗震安全性进行评估。

关键词： 抗震性能； 既有建筑； 动力测试； 状态识别； 快速评估

中图分类号： TU311.3；TU352.1    文献标志码： A    文章编号： 1004-4523（2024）05-0802-10

DOI： 10.16385/j.cnki.issn.1004-4523.2024.05.008

引  言

随着城镇化进程的加快，中国已建成体量巨大的城市建筑群与基础设施网络，城市工程系统的防震减灾面临新挑战。在主要自然灾害中，地震具有突发性强、破坏性大、影响范围广等特点，严重威胁中国城市安全与社会发展。目前，中国人口超过百万的城市大部分位于6度以上抗震设防区［1］，且中国西部地区仍然处于7级以上强震的活跃时段［2］。近年来的全球地震事件表明，一次强震后往往伴随余震序列作用，例如2010年的8.8级智利主震2个月内伴随21次6.0级以上余震，带来地震后既有建筑安全评估的时效性要求。与之相呼应，中国防震减灾规划提出小时级别的震后评估要求，即在地震后1小时内提供震灾快速评估结果，2小时内提供人员伤亡、房屋破坏初步信息和辅助决策建议［2］。可以看到，传统依靠专家赶赴现场及基于经验的定性判定已无法充分满足大范围地震现场应急评估的发展要求。因此，城市既有建筑（群）的地震安全性评价面临高效分析、快速评估、定量判定的多重技术发展需求，尚待建立与结构抗震性能水准（正常运行、立即使用、生命安全、倒塌阻止）间的映射关系。

一方面，工程结构在其全寿命期内不可避免地存在结构性能退化的现象，特别是地震频发区的建筑结构存在地震累积损伤的现象，上述情况均会导致结构服役状态演化并带来不确定的问题。以模态频率为特征量，日本东京多幢建筑在2011年东日本大地震后结构基频出现永久下降［3］，某68层高层结构在强台风后第一阶模态频率下降了9%［4］。另一方面，考虑建筑结构的个性化特点，现有结构动力特性经验预测公式可能存在理论力学模型和训练数据集覆盖范围的局限性。例如，基于瑞利方法的理论力学模型无法充分考虑填充墙的贡献，部分国家将由瑞利方法推导的结果作为结构自振周期的上限［5］。已有研究表明动力特性经验公式回归分析中，回归系数随样本数据集的不同而存在显著差异［6］。因此，针对既有建筑的安全性评价，需要结构本身和当地地震动等实测数据与信息，以标定结构真实服役状态，保证结构抗震性能评估结果的准确性，并兼顾结构抗震性能分析的准确性和时效性。

结构健康监测通过测量结构在环境激励或动力荷载（风、地震等）下的振动响应，结合信号分析与系统识别理论，可以有效识别结构服役状态并进行安全性评价［7?8］。目前，国内外学者已发展了一系列数据驱动型状态评价指标，用于强震下的震损结构安全评价。以美国Van Nuys酒店为基准评估对象［9］，国内外学者主要采用模态频率、瞬时均值频率、层间位移角、楼层侧向刚度、平均剪切波速等评估指标［3，10］。需要注意的是，受限于监测数据和结构信息的不完备性，监测型结构状态评价指标主要集中于时序信号统计特征（峰值、均方根值等）、响应信号特征（结构动力特性）、模型力学参数等维度，用于识别结构服役状态和灾后损伤，尚缺乏与结构抗震安全性和性能水准间的直接联系。

不同于结构健康监测的数据驱动型评价指标，结构抗震安全性评估依赖于不同尺度的结构数值分析模型。从不同的分析场景出发，结构抗震安全性评估可以采用有限自由度系统、缩聚力学模型和有限元计算模型，并进一步进行基于结构建模的动力响应计算与易损性分析［11］。但是，不同于经典的结构性能正向分析，既有建筑结构的动力建模是一类典型的动力学反演问题，存在模型精细度选择、监测数据不完备、模型参数可识别的耦合问题［12］。一方面，考虑工程对象的体系复杂性，其数值分析模型与复杂物理结构间不可避免地存在建模误差（Modeling Error），限制了高保真、参数全局最优结构分析模型的识别与建立［13?14］。另一方面，既有建筑结构的震害预测数值分析方法，例如FEMA规范中的HAZUS方法［15］，往往只考虑结构的第一阶模态。因此，针对既有建筑服役状态的数值映射，可以选择保留主要可观测模态或动力自由度的结构缩聚模型，一方面能有效兼顾结构时程分析中对计算模型的要求，并适应结构真实状态信息不完备的客观约束；另一方面能保证现场快速动力测试条件下目标数值模型参数的可识别性。

本文以既有建筑抗震性能快速评估为目标，通过结构动力测试与状态识别方法，提出了映射真实结构服役状态的等效单自由度非线性模型建模方法，并给出了针对结构损伤状态和抗震性能水准的两类评价指标。以四川当地某12层高层规则框架结构和当地地震台站真实地震动为例，系统展示了本文提出的方法可用于不同地震事件下的抗震安全性评估与预警。

1 既有建筑状态识别与抗震性能快速评估方法

1.1 评估方法设计

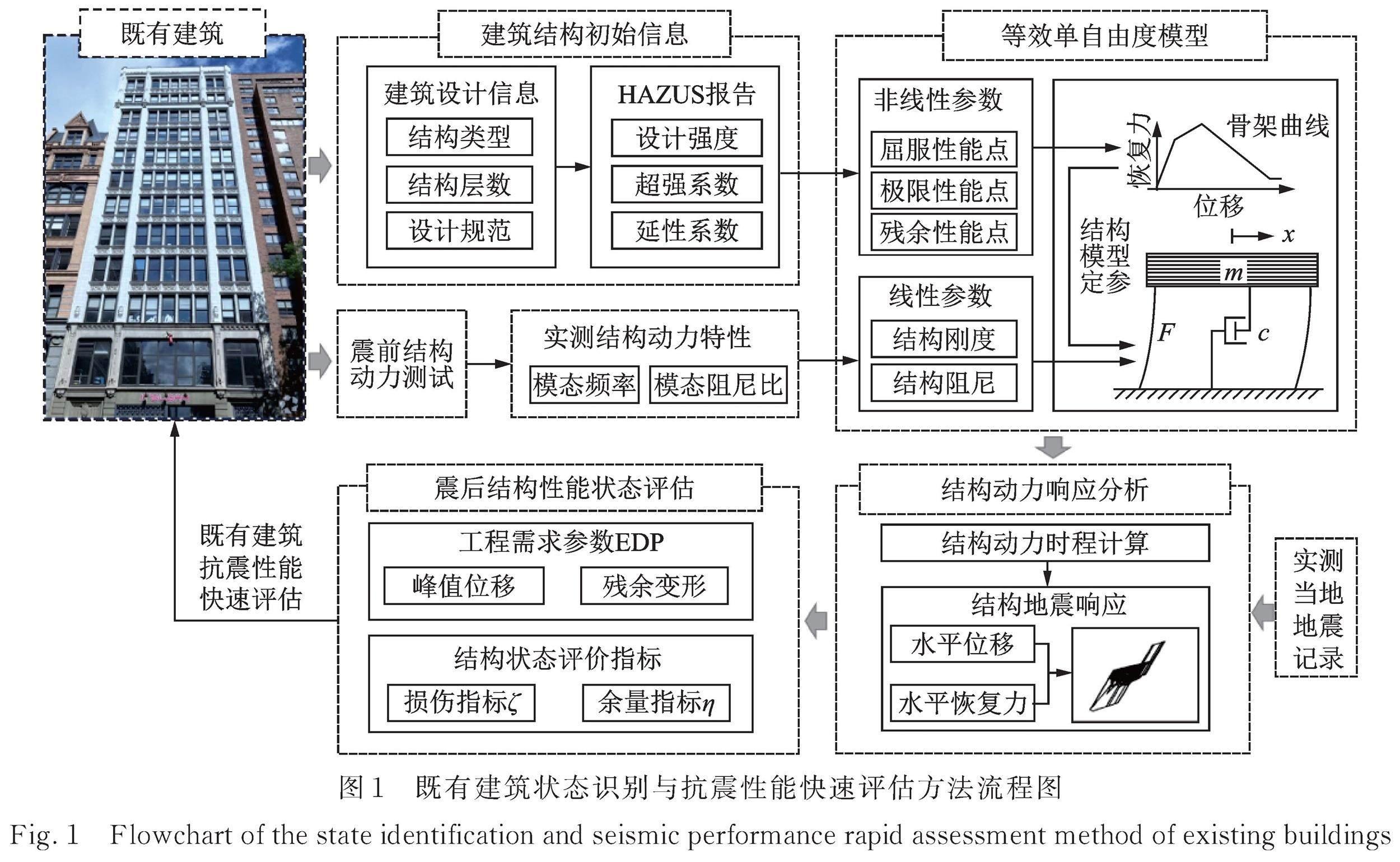
本文所提出的面向既有建筑结构的既有建筑状态识别与抗震性能快速评估方法，总体上包括客观性建筑结构信息提取、结构动力测试与状态识别、等效单自由度非线性模型构建、结构动力响应分析与性能评估四个步骤，分析流程以及各个步骤的主要内容如图1所示。

首先应进行建筑结构初始信息的提取工作。主要是通过调取目标建筑工程竣工资料，提取该建筑的结构类型、建造年代、层数、抗震设防类别等一系列建筑与结构的基本特征，相关特征将用于后续基于HAZUS报告的结构类型及其非线性参数的确定。

其次是目标结构的现场动力测试与识别工作。这一阶段的主要工作是在破坏性地震发生前即既有建筑处于完好状态时，根据目标建筑的平面分布情况布置传感器测点，进行结构现场动力测试，进一步通过分析结构动力响应数据识别目标建筑当前的模态频率和阻尼比，二者分别对应了结构完好线性状态的抗侧刚度和耗能能力，可作为等效模型线性参数计算和后续地震激励下结构状态评估的重要依据。

在初始信息提取和动力测试、识别均完成后，即可进入目标建筑等效单自由度建模步骤。非线性模型以结构抗震安全性分析为目标，通过动力测试与模态识别确认结构的刚度与阻尼参数，通过HAZUS报告确定结构非线性本构模型的一系列关键参数，最终建立具有屈服性能点、极限性能点和残余性能点的等效三折线本构模型，用于分析该建筑在不同地震动作用下的弹塑性动力响应。

最后一步是结构性能的快速评估工作。以前三步建立的结构动力模型为基础，分析时选用建筑当地真实强震观测台站记录的地震动时程作为输入，完成动力弹塑性时程分析，得到响应时程。之后利用针对结构损伤状态和抗震性能水准的两类评价指标对结构性能状态进行快速评估，并依据评估结果对既有建筑的抗震安全性和潜在破坏性地震动特性进行评价与预警。具体操作时，分析人员可选用常见的地震动强度参数对地震动时程记录进行调幅处理，以研究结构响应和结构性能状态等在不同调幅因子下的差异和变化趋势。

1.2 状态识别与建模

既有建筑的结构动力测试受制于测点数量和布置位置等现场约束，环境激励下结构仅有有限数量的低阶模态可以被充分激发并具备相对可靠的识别结果。等效单自由度非线性模型是结构动力分析中的一类经典模型，对规则型建筑具有相对可靠的分析精度［16?17］，被广泛应用于结构地震易损性分析［18］、倒塌分析［17］等问题。美国HAZUS技术手册也主要基于结构第一阶模态信息建立分析模型。因此，权衡考虑动力测试便捷性、状态识别可靠性、计算模型精度与效率，本文将等效单自由度模型用于结构动力时程分析与震后性能状态评估中。

本文提出的既有建筑抗震性能快速评估方法主要采用动力测试和等效单自由度非线性模型，以同时满足既有建筑状态标定和抗震安全性分析。用于映射既有建筑的等效单自由度非线性模型的动力学方程如下式所示：

为了降低对结构信息的依赖性和建筑真实质量估计的不确定性，考虑到既有建筑现场动力测试主要以识别模态频率和模态阻尼比为主，本文将公式（1）进一步进行质量归一化，得到等效单自由度非线性模型的动力学方程为：

式中为圆频率；为阻尼比；为质量归一化的恢复力。相关变量的关系为：，。

在HAZUS将Pushover曲线转化为与建筑物基本周期相关的A?D格式的能力谱曲线的过程中，对应的分析模型也转化为具有单位质量的等效单自由度非线性模型，形式上与公式（2）类似。用HAZUS中能力谱曲线的谱加速度替代，用HAZUS中能力谱曲线的谱位移替代，令为结构的一阶模态阻尼比，则由公式（2）即可描述骨架曲线为A?D格式、质量为单位质量的等效单自由度非线性模型。

进一步观察公式（2）可以发现，等效单自由度非线性模型主要涉及两类参数的识别与确定，包括结构线性状态参数（第一阶模态频率f与阻尼比）和结构非线性恢复力模型的性能特征点（例如三折线模型的屈服点、最大承载力点和极限变形点）及其对应参数。

针对结构线性状态参数，本文主要依靠结构现场动力测试来获得。按激励来源划分，既有建筑动力测试时主要分为人工激励和环境激励两类方法。其中，环境激励下的结构模态识别无需外界施加激励，动力测试期间不影响结构的正常使用，且能避免人工激励不当引起的结构损伤，因此适用于大量建筑结构的动力特性识别研究与实践［7， 19］。在进行环境激励下的结构动力测试时，水平传感器测点应沿结构高度布置在对应模态振型曲线上位移较大的位置。考虑环境激励下的前几阶特别是第一阶模态最容易被激发和观测，结合等效单自由度模型主要利用结构纵向和横向的第一阶模态特征，本文在进行动力测试时直接在顶层布置传感器［19?20］，同时为了区分第一阶平动模态和第一阶扭转模态，在顶层远离结构刚心的位置处额外布置一个水平向测点。在某一频率下，位于质心测点和角部测点的波峰幅值相同或接近时，该频率可识别为平动模态；当角部测点的波峰幅值显著高于质心测点时，该频率可识别为扭转模态。在获得既有建筑顶层两个方向的动力响应数据后，可以利用各类结构模态识别理论与方法，快速且准确地识别出结构前几阶的模态频率与阻尼比。例如基于频域特征的峰值拾取法和半功率带宽法、基于时域特征的随机子空间法、基于时/频域分析的小波变换和HHT方法以及贝叶斯概率方法等［21?23］。考虑既有建筑的相对小阻尼特性，并且从数据分析的鲁棒性和便捷性角度出发，本文选用了经典的峰值拾取与半功率带宽法来识别结构的自振频率和阻尼比［21?22］。

通过识别目标结构纵向和横向的第一阶模态频率和阻尼比，计算得到公式（2）中等效单自由度模型的两个关键线性状态参数和。在此基础上，本文进一步提出基于HAZUS技术手册确定等效模型的非线性模型参数，具体步骤包括：（1）HAZUS中将建筑按照结构类型和层数分成了36个类别。本方法根据建筑信息档案和现场调研结果，提取结构的类型、层数、高度和建造年代等关键信息，确定HAZUS中的目标建筑类别，并结合结构抗震设防等级计算得到屈服超强系数、峰值超强系数、延性系数等性能参数；（2）利用给定的能力谱曲线屈服点和峰值点的计算公式，结合结构基本信息和动力测试结果，通过两类性能点（屈服点、峰值承载力点）定义目标结构在纵向和横向的抗侧恢复力非线性模型。为了模拟出结构的刚度退化和倒塌临界状态，引入一类能力谱曲线修正方法［24?25］对上述骨架曲线进行合理修正。其中，屈服点（）的修正按照等效面积法进行，峰值承载力点（）的修正按照下式进行：

（3）

（4）

极限变形点（）在HAZUS中未作规定，属于新引入的性能点，按照下式计算得出：

式中为延性系数；为基于HAZUS得到的修正前的峰值谱加速度；为修正后的屈服谱位移；为修正后的屈服谱加速度；为修正后的峰值谱位移；为修正后的峰值谱加速度；为修正后的极限谱加速度；为修正后的极限谱位移；和分别为HAZUS中完全破坏和严重破坏对应的谱位移阈值。

已有研究表明，滞回规则对此类模型的动力分析结果影响相对较小［26］，依照已有研究经验与分析对比结果，本文研究工作选用了Pinching4材料本构模型。

1.3 状态与性能评估

根据1.2节修正建立的恢复力骨架曲线及其三类性能点参数，建立结构不同变形状态与正常运行（Operational，OP）、立即使用（Immediate Occupancy，IO）、生命安全（Life Safety，LS）、倒塌阻止（Collapse Prevention，CP）等结构抗震性能水准之间的直接关系，如图2所示。一般情况下，四类抗震性能水准OP，IO，LS和CP往往与结构无损、轻微破坏、中等破坏和严重破坏等四类损伤状态存在相关性。为了区分结构的LS和CP性能状态，参考混凝土构件试验中取最大承载力下降15%时的点为破坏点（此时构件严重破坏）的一般方法，本文在峰值承载力点和极限变形点间增加了一个性能点（），定义该点的承载力为峰值承载力点的85%。

地震工程的研究表明结构地震损伤往往具有峰值与累积效应。近年来，文献［27?28］提出一类基于监测数据驱动的非线性损伤评估指标，可直接用于本文目标结构的损伤状态评估，如下式所示：

相关指标已完成了一系列大尺度振动台试验验证［27?28］。为了直观表述某次地震下目标结构抗震性能与相应性能水准之间的关系，本文构建了余量指标，其数学表达式如下式所示：

式中为峰值谱位移；和分别为峰值和累积项对应的权重，已有研究表明一般取为0.85和0.15［27?28］；为控制模型评估值增长趋势与速率的参数，取为2.5；为峰值谱位移所在滞回环对应线性程度的回归统计参数；和分别为峰值谱位移所在滞回环对应的结构等效刚度和等效单自由度模型线弹性段的刚度；和分别表示谱位移响应追踪误差和谱位移响应的均方根值。

该数据驱动型指标不依赖于结构先验性的滞回行为及非线性特征，可用于真实结构强震观测和震损评估。在本文研究中，该指标用于量化评估不同地震激励下既有建筑等效单自由度模型的损伤程度。另一类结构能力余量指标是归一化评价指标，指标值在0～1之间，用于考察单一地震动作用后结构的抗震性能及能力储备，并映射三折线模型四类抗震性能点区分的五类抗震性能水准。当偏小时，目标结构抗震性能水准可能处于倒塌阻止或倒塌水准，此时监控管理部门应及时发出预警。

2 既有建筑案例

2.1 目标建筑基本信息

四川省宜宾市下辖的珙县位于华蓥山断裂带附近，该断裂带具有中强破坏性地震地质条件。根据四川省地震台网的公开数据，仅在2020年当地就发生多次四级以上的有感地震。为了对珙县重要既有建筑进行抗震安全性与风险分析，本文研究团队于2021年数次前往珙县当地进行建筑结构信息提取与一系列现场动力测试。和谐苑小区一号楼是当地一栋12层居民住宅楼，其主要建筑与结构信息汇总如表1所示。该建筑结构体系为框架结构，结构层数为12层，是当地较高的框架结构，并且与HAZUS中对应的C3H类别的典型层数一致，具有建筑样本的代表性且存在较高的评估价值。

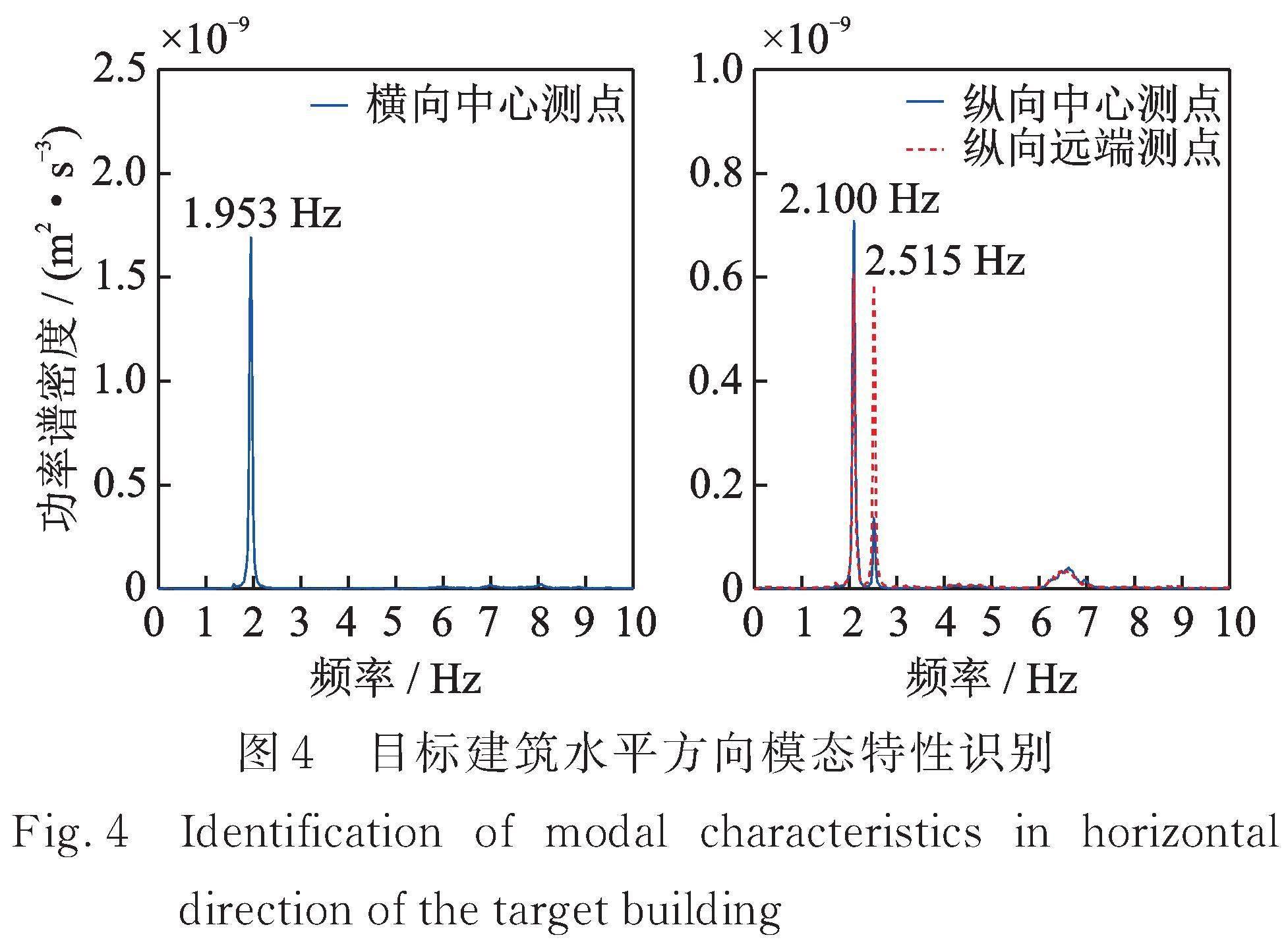
图3所示为目标建筑物外立面情况与现场动力测试状况。考虑到本文所提出的方法仅需要目标建筑两个水平方向的第一阶模态特性，根据1.2节中的说明，选择在目标建筑顶部第12层开展现场动力测试。考虑到测试现场条件约束，中心测点和远端测点布置如图3中心“测点平面布置”所示。采样频率取为200 Hz，采样时长为900 s。绘制3个测点加速度时程对应的功率谱如图4所示。识别得到目标建筑的横向一阶模态频率为1.953 Hz，纵向2.100 Hz处远端测点和中心测点的峰值比为0.91，接近1.0。与之不同，2.515 Hz处的峰值比为4.30，两个测点间差异较大。因此，基本可判断2.1 Hz为第一阶平动模态，2.515 Hz对应扭转模态。利用经典半功率点法，识别目标建筑横向和纵向第一阶模态阻尼比分别为0.0123和0.0085。本次分析的FFT长度为8192，频率分辨率为0.0244 Hz。

2.2 实际地震动输入

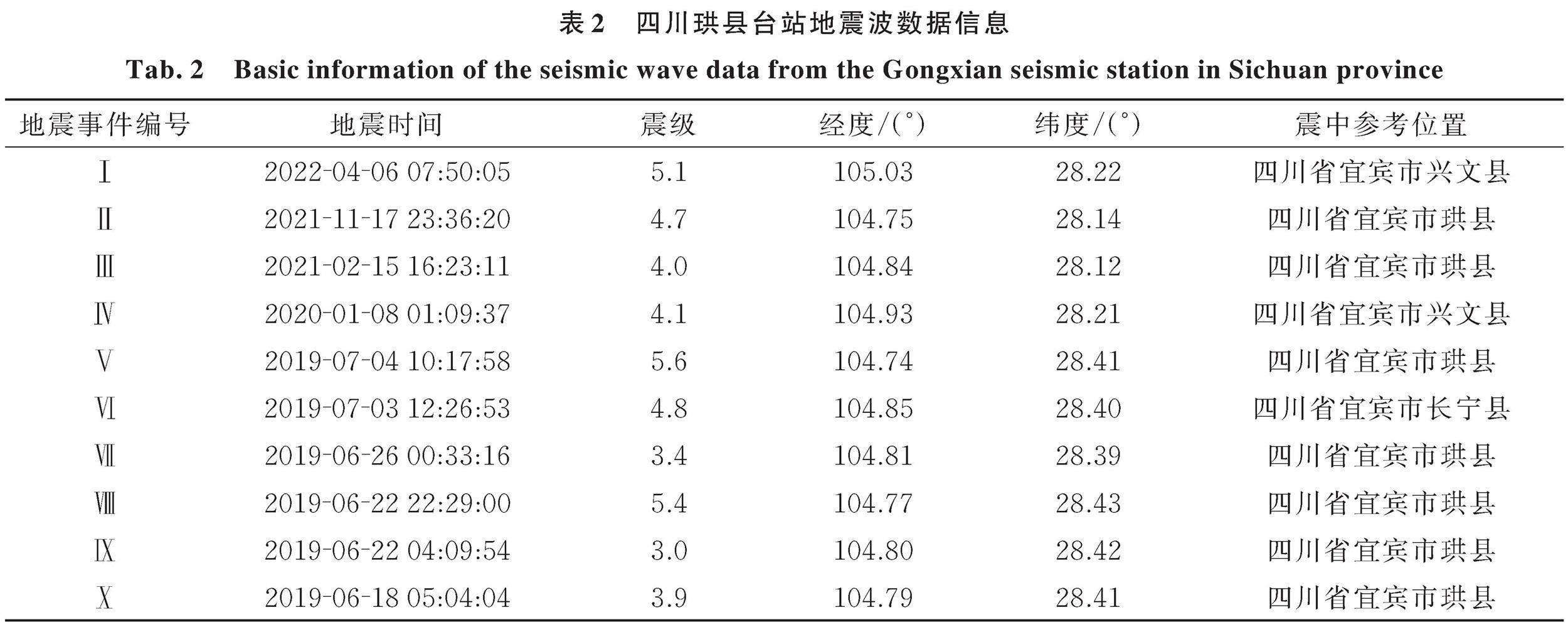
四川省宜宾市珙县周边在2019至2022年间发生了多次有感地震，包括2019年7月的M5.6级珙县地震。四川省地震台在目标建筑所在地设置了珙县中学台站（51GXT），取得了一系列地震动记录。本次分析选用该台站在此期间记录到的10条典型地震波记录，编号为Ⅰ～Ⅹ，各地震波数据的基本信息如表2所示。

针对每次地震事件，将记录的地震波两个水平方向的加速度时程作为目标建筑纵向和横向等效单自由度模型的激励输入，进行一系列非线性时程计算。考虑到各地震波的峰值加速度（PGA）并不一致，选用动力放大系数谱进一步展示和对比各条波的频谱特性与目标结构自振周期的关系，如图5所示。

从图5中可以看出，抗震规范［29］的动力放大系数曲线与实测的当地地震动结果在形状上相似，但数值上具有一定的差异。本文示例的12层框架结构自振周期位于动力放大系数的下降段，对应的实际地震动放大系数比规范值偏小。

2.3 目标建筑性能评估

根据表1中的建筑基本信息从HAZUS技术手册中得到建筑的结构类型以及屈服超强系数等参数，再将识别得到的目标结构纵向和横向第一阶模态频率和阻尼比代入手册中的相关公式计算屈服点（）和峰值承载力点（），最后按1.2节叙述的方法建立结构两个方向的等效单自由度模型：（1）横向，屈服点（）为（0.1239g，0.0081 m），峰值承载力点（）为（0.1608g，0.0202 m），极限变形点（）为（0.0248g，0.0511 m）；（2）纵向，屈服点（）为（0.1239g，0.0070 m），峰值承载力点（）为（0.1608g，0.0175 m），极限变形点（）为（0.0248g，0.0442 m）。分析动力模型在表2中10条地震波作用下的结构动力响应，非线性分析算法采用牛顿?拉夫森算法，积分方法采用。典型结构动力响应与恢复力滞回曲线如图6所示，其中，恢复力，屈服恢复力，表示单位质量。

在事件Ⅵ的地震波作用下，结构在两个方向上均处于线弹性状态；事件Ⅴ对应的结构响应稍大，结构在横向仍基本处于线弹性状态，但纵向已初步进入了非线性状态；事件Ⅷ对应的结构响应在这三者中最大，结构在两个方向上均进入了弹塑性状态，且纵向的滞回环在三者中最为饱满，非线性行为相对明显。

表3列出了所有地震输入下的计算和评价结果，可以看出，除地震动Ⅴ和Ⅷ作用下目标建筑进入了IO状态外，其余地震事件下结构均处于OP状态，这与目标建筑在历次地震后均未发现可见损伤，且处于正常或立即使用状态的人工现场调研情况相符。地震动Ⅴ和Ⅷ与剩余八个地震动对目标建筑地震响应存在差异的原因可能是二者的PGA显著高于其余地震动。模型响应方面，对比地震动Ⅴ和Ⅷ下的结果，可见残余变形和损伤指标非零时结构均进入IO状态，故根据这两个指标均能直观地判断结构是否存在一定的地震损伤。但与残余变形相比，损伤指标对损伤程度的变化更敏感。仍以地震事件Ⅴ和Ⅷ的结果为例，与Ⅷ相比，Ⅴ的纵向残余变形增加了1倍，而损伤指标相应地增加了1.3倍，变化程度略高于残余变形。故在分析结构是否产生损伤以及结构损伤的程度时，可以优先参考损伤指标。

为考察目标建筑的抗震性能，利用动力时程分析结果计算各地震事件下目标建筑的余量指标，计算结果如图7和8所示。结果显示，所有地震事件下其结构抗震性能均能满足IO水准的要求，且计算所得余量指标与LS水准间有一定冗余，这说明以IO水准为要求时目标建筑的抗震性能在这10次地震中是达标的。同一地震事件在不同方向上的余量指标存在差异，这与目标建筑自身在两个方向上的抗震性能差异以及地震动方向性差异有关，进一步说明了从两个方向而非单一方向考虑抗震性能的必要性。综上，本文提出的余量指标能够直观地反映历次地震中目标建筑两个方向上的抗震性能与各性能水准需求之间的关系。此外，与残余变形和损伤指标相比，余量指标可以反映结构震后仍处于线性状态时的动力响应程度；与峰值谱位移相比，余量指标是1～0的归一化指标，能更好地反映“冗余度”的概念。

基于上述讨论，选用结构抗震性能余量指标为评价指标，借鉴增量动力分析（IDA）方法的思想，以PGA为地震动强度参数调幅现有实测地震波，进一步识别潜在危险地震动并评估目标建筑的抗震安全性。PGA的调幅范围为0.05g～0.40g，调幅间距取为0.05g，两个方向10次地震事件共计生成80条地震波输入记录，每条调幅地震动的结构动力分析及抗震性能余量指标结果如图9所示。结果显示，余量指标随PGA的增大总体上呈递减趋势，而相同PGA下不同地震波在不同方向导致的结构响应存在显著差异。本文按照地震动调幅后对应的抗震性能水准将地震动分为敏感（调幅后能达到LS?CP状态）、次敏感和不敏感（调幅至0.4g时仍未达到OP水准）三类。地震事件Ⅰ和Ⅲ对应的地震波，调幅至0.2g时已能在两个方向上使得结构进入CP水准，对于目标建筑该地震动属于敏感型。其余地震动在两个方向上的敏感性需做进一步讨论，例如事件Ⅱ在横向调幅至0.4g时目标建筑仍处于OP状态，对该建筑而言属于不敏感地震动，但在纵向调幅至0.25g时目标建筑已处于IO状态，此时属于次敏感型地震动。由图5可以推测，目标建筑对地震事件Ⅰ和Ⅲ对应的地震波敏感的原因可能是Ⅰ和Ⅲ对应的动力放大系数高于其余地震。

3 结  论

既有建筑的高效、快速、定量抗震性能评估方法对城镇既有建筑（群）的地震安全性及震后应急评估工作具有重要意义。本文提出利用结构动力测试与强震动观测获取既有建筑和当地地震的实测数据与信息，在此基础上，利用等效非线性单自由度模型映射实测结构服役状态与初始建筑设计信息，利用当地强震观测信息，建立既有建筑状态识别与抗震性能快速评估方法。首先阐述了针对既有建筑的等效非线性单自由度模型建立方法，重点说明了利用实测动力特性结果和HAZUS技术手册得到等效单自由度模型及其非线性本构等效修正的方法，使得模型能够反映真实结构在地震作用下的刚度退化和损伤累积行为。在此基础上，利用常见的工程性能参数（峰值谱位移、残余变形）和本文提出的两类结构状态评价指标（损伤指标、余量指标），建立了等效模型与四个抗震性能水准之间的直接联系。本文以四川省珙县当地一栋12层高层规则框架结构为例，基于当地强震台站在2019至2022年间10次实测地震动数据，进行了目标建筑的抗震安全性评估，并比较了各参数、指标间的特点与差异。分析结果表明，目标建筑在近期地震动作用下结构抗震性能水准主要为正常运行（OP）状态，少数地震动输入下结构处于立即使用（IO）状态。进一步，结合实测模型，对一系列地震动对目标建筑的危险性进行了分析与评价。

目前，受限于真实结构的有限观测条件与信息的不完备，本文方法主要采用等效单自由度模型，无法充分考虑既有结构地震响应中潜在的高阶模态效应或空间扭转效应，在应用于高层或复杂结构时会存在一定的误差。因此，本文方法建议的分析对象为以一阶模态为主的简单规则多层建筑。未来研究工作将考虑多自由度三维力学模型与模型更新技术，以获得更高保真度的既有建筑服役状态映射模型。

参考文献：

［1］杨静， 李大鹏， 翟长海， 等. 城市抗震韧性的研究现状及关键科学问题［J］. 中国科学基金， 2019， 33（5）： 525?532.

YANG Jing， LI Dapeng， ZHAI Changhai， et al. Key scientific issues in the urban earthquake resilience［J］. Bulletin of National Natural Science Foundation of China， 2019， 33（5）： 525?532.

［2］国家发展改革委， 中国地震局.关于印发《防震减灾规划 （2016―2020年）》的通知［R/OL］. （2016?11?17） ［2022?09］. https： //www.ndrc.gov.cn/xxgk/zcfb/ghwb/201612/t20161202_962210.html？code=&state=123.

National Development and Reform Commission，China Earthquake Administration. Notice of issuing “The National Earthquake Hazards Prevention and Reduction Program （2016―2020）”［R/OL］. （2016?11?17） ［2022?09］. https：//www.ndrc.gov.cn/xxgk/zcfb/ghwb/201612/t20161202_962210.html？code=&state=123.

［3］单伽锃， 王律己， 余桦， 等. 结构强震观测与评估研究现状与展望［J］. 工程力学， 2022， 39（11）： 1?12.

SHAN Jiazeng， WANG Lüji， YU Hua， et al. State-of?the?art review on structural seismic monitoring and assessment of building structures［J］. Engineering Mechanics， 2022， 39（11）： 1?12.

［4］ZHOU K， LI Q S. Effects of time‐variant modal frequencies of high‐rise buildings on damping estimation［J］. Earthquake Engineering & Structural Dynamics， 2021， 50（2）： 394?414.

［5］阎红霞， 杨庆山， 秦敬伟， 等. 各国规范中RC框架自振周期的对比和探讨［J］. 振动与冲击， 2012， 31（11）： 108?113.

YAN Hongxia， YANG Qingshan， QIN Jingwei， et al. Comparison and comment for computing natural vibration period of RC frames in codes of some countries［J］. Journal of Vibration and Shock， 2012， 31（11）： 108?113.

［6］HONG L L， Hwang W L. Empirical formula for fundamental vibration periods of reinforced concrete buildings in Taiwan［J］. Earthquake Engineering & Structural Dynamics， 2000， 29（3）： 327?337.

［7］杨朋超， 薛松涛， 谢丽宇. 消能减震建筑结构模态参数识别的贝叶斯方法［J］. 振动工程学报， 2021， 34（4）： 671?679.

YANG Pengchao， XUE Songtao， XIE Liyu. Bayesian modal parameters identification of passively controlled building structures［J］. Journal of Vibration Engineering， 2021， 34（4）： 671?679.

［8］杨朝勇， 茅建校， 王浩， 等. 贝叶斯方法在大跨度斜拉桥模态参数识别中的应用研究［J］. 振动工程学报， 2022， 35（3）： 691?698.

YANG Chaoyong， MAO Jianxiao， WANG Hao， et al. Application study on Bayesian method in modal parameter identification of the long?span cable?stayed bridge［J］. Journal of Vibration Engineering， 2022， 35（3）： 691?698.

［9］KRAWINKLER H. Van Nuys hotel building testbed report： exercising seismic performance assessment： PEER Report 2005/11［R］. Berkeley： University of California， Berkeley， 2005： 49?85.

［10］董银峰， 李英民， 赖明. 基于EMD和VARMA模型的结构损伤识别［J］. 振动与冲击， 2010， 29（12）： 141?147.

DONG Yinfeng， LI Yingmin， LAI Ming. EMD and VARMA model based structural damage detection［J］. Journal of Vibration and Shock， 2010， 29（12）： 141?147.

［11］马林林， 薛建阳， 张锡成. 残损古建筑木结构的地震易损性分析［J］.振动工程学报， 2023，36（5）： 1390?1401.

MA Linlin， XUE Jianyang， ZHANG Xicheng. Seismic vulnerability analysis of damaged ancient timber structures［J］. Journal of Vibration Engineering， 2023，36（5）： 1390?1401.

［12］SHAN J Z， ZHANG H Q， SHI W X， et al. Health monitoring and field?testing of high?rise buildings： a review［J］. Structural Concrete： Journal of the FIB， 2020， 21（4）： 1272?1285.

［13］SHAN J Z， OUYANG Y T， YUAN H L， et al. Seismic data‐driven identification of linear models for building structures using performance and stabilizing objectives［J］. Computer?Aided Civil and Infrastructure Engineering， 2016， 31（11）： 846?870.

［14］翁顺， 朱宏平. 基于有限元模型修正的土木结构损伤识别方法［J］. 工程力学， 2021， 38（3）： 1?16.

WENG Shun， ZHU Hongping. Dynamic identification of civil structures based on finite element model updating［J］. Engineering Mechanics， 2021， 38（3）： 1?16.

［15］HAZUS?MH MR1. Multi?hazard loss estimation methodology， earthquake model， HAZUS?MH 2.1， technical manual［R］. Washington， D.C.： Federal Emergency Management Agency， 2013： 96?106.

［16］REULAND Y， LESTUZZI P， SMITH I F C. An engineering approach to model?class selection for measurement?supported post?earthquake assessment［J］. Engineering Structures， 2019， 197： 109408.

［17］余丽玲， 李钢， 李宏男. 考虑往复退化的倒塌分析等效单自由度模型［J］. 地震工程与工程振动， 2018， 38（6）： 52?63.

YU Liling， LI Gang， LI Hongnan. Equivalent single-degree?of?freedom model considering cyclic deterioration for collapse analysis［J］. Earthquake Engineering and Engineering Dynamics， 2018， 38（6）： 52?63.

［18］耿飞， 徐超， 温增平. 基于单自由度等效线性化模型的RC结构地震易损性分析［J］. 震灾防御技术， 2022， 17（2）： 316?325.

GENG Fei， XU Chao， WEN Zengping. Fragility analysis of RC frame structures based on equivalent linearization method of SDOF system［J］. Technology for Earthquake Disaster Prevention， 2022， 17（2）： 316?325.

［19］SHAN J Z， SHI W X， WANG J. Regional study on structural dynamic property of buildings in China［J］. Earthquake Engineering & Structural Dynamics， 2013， 42（7）： 1013?1029.

［20］蒲黔辉， 洪彧， 王高新， 等. 快速特征系统实现算法用于环境激励下的结构模态参数识别［J］. 振动与冲击， 2018， 37（6）： 55?60.

PU Qianhui， HONG Yu， WANG Gaoxin， et al. Fast eigensystem realization algorithm based structural modal parameters identification for ambient test［J］. Journal of Vibration and Shock， 2018， 37（6）： 55?60.

［21］陈伏彬， 李秋胜. 基于环境激励的大跨结构动力特性识别［J］. 地震工程与工程振动， 2015， 35（1）： 58?65.

CHEN Fubin， LI Qiusheng. Identification of dynamic characteristics of large?span structure based on the ambient excitation［J］. Earthquake Engineering and Engineering Dynamics， 2015， 35（1）： 58?65.

［22］薛建阳， 吴晨伟， 浩飞虎， 等. 应县木塔动力特性原位试验及有限元分析［J］. 建筑结构学报， 2022， 43（2）： 85?93.

XUE Jianyang， WU Chenwei， HAO Feihu， et al. In situ experiment and finite element analysis on dynamic characteristics of Yingxian wooden tower［J］. Journal of Building Structures， 2022， 43（2）： 85?93.

［23］尹涛， 尹孟林， 贾晓健. 有限长周期支撑结构贝叶斯概率损伤识别研究［J］. 振动工程学报， 2018， 31（1）： 91?101.

YIN Tao， YIN Menglin， JIA Xiaojian. Bayesian probabilistic damage detection in a laboratory periodically-supported structure of finite?length［J］. Journal of Vibration Engineering， 2018， 31（1）： 91?101.

［24］RYU H， LUCO N， BAKER J W， et al. Converting HAZUS capacity curves to seismic hazard compatible building fragility functions： effect of hysteretic models［C］∥Proceedings of the 14th World Conference on Earthquake Engineering： Innovation， Pratice，Safety. Beijing： International Association for Earthquake Engineering， 2008： 469.

［25］RYU H， LUCO N， UMA S R， et al. Developing fragilities for mainshock?damaged structures through incremental dynamic analysis［C］∥Proceedings of the Ninth Pacific Conference on Earthquake Engineering. Auckland， New Zealand： Macquarie University， 2011： 225.

［26］LUCO N， BAZZURRO P， CORNELL A. Dynamic versus static computation of the residual capacity of a mainshock?damaged building to withstand an aftershock［C］∥Proceedings of the 13th World Conference on Earthquake Engineering. Vancouver， Canada： International Association for Earthquake Engineering， 2004： 2405.

［27］SHAN J Z， SHI W X， L? X L. Model?reference health monitoring of hysteretic building structure using acceleration measurement with test validation［J］. Computer?Aided Civil and Infrastructure Engineering， 2016， 31（6）： 449?464.

［28］SHAN J Z， ZHANG H Q， OUYANG Y T， et al. Data?driven damage tracking and hysteresis evaluation of earthquake?excited structures with test validation［J］. Engineering Structures， 2020， 207： 110214.

［29］中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局. 建筑抗震设计规范： GB 500011—2010（2016年版）［S］. 北京： 中国建筑工业出版社， 2016.

Ministry of Housing and Urban-Rural Development of the Peoples Republic of China， General Administration of Quality Supervision，Inspection and Quarantine of the Peoples Republic of China.Code for seismic design of buildings： GB 50011—2010（2016 ed.） ［S］. Beijing： China Architecture & Building Press， 2016.

State identification and seismic performance rapid assessment of existing regular building structures by considering field measured information

Abstract： The seismic safety evaluation of existing urban buildings （groups） is faced with multiple technical development of efficient analysis， rapid evaluation and quantitative determination. Considering the evolution of structural performance during the long-term service life， the safety evaluation of in-service buildings requires design and measurement information on the structures as well as regional ground motions to calibrate the real conditions of the structures， which can ensure the accuracy of the performance evaluation results within an acceptable timeliness. Based on the equivalent nonlinear single-degree-of-freedom model and the authors recent research on data-driven performance assessment index， this study proposes a method to map the global conditions of the structure with the measurement modal information and assess the seismic safety of the target building using the regional dataset of measured ground motion further. Based on the field testing and the HAZUS technical manual， the procedure of establishing the equivalent nonlinear single-degree-of-freedom representing the existing building is described. Two structural condition evaluation indicators are proposed， combined with multivariate engineering performance parameters， and the relationship between the deformation of an equivalent model and different seismic performance levels is further established. A high-rise regular RC frame structure located in Gongxian， Sichuan Province is considered as an example， the seismic safety of this building subjected to 10 local earthquakes measured from 2019 to 2022 is evaluated.

Key words： seismic performance； existing building； dynamic test； state identification； rapid assessment