直升机超临界尾传动轴干摩擦阻尼器碰摩响应边界特性分析
2024-06-15金晟宋立瑶曹鹏李坚游有鹏朱如鹏王旦
金晟 宋立瑶 曹鹏 李坚 游有鹏 朱如鹏 王旦

摘要: 为最大化提高直升机功重比,越来越多的直升机设计中应用了超临界尾传动系统,这一系统会导致跨临界振动的产生。安装干摩擦阻尼器是一种常见的抑制直升机尾传动轴跨临界剧烈振动的方法。以某装有干摩擦阻尼器的尾传动轴为研究对象,建立控制方程,并分析系统在传动轴偏心激励下各类碰摩响应的边界特性。建立传动轴/阻尼器系统的非线性控制方程;依据扫频获得系统典型碰摩响应特征,使用解析法针对无碰摩响应求解碰摩发生边界,并对同频全周碰摩响应求解其稳定性条件的边界;通过Runge?Kutta法验证了所推导的响应边界,并探讨了响应边界与系统参数的影响关系。
关键词: 超临界尾传动轴; 干摩擦阻尼器; 碰摩; 响应特性; 稳定性分析
中图分类号: V214.19 文献标志码: A 文章编号: 1004-4523(2024)05-0756-14
DOI:10.16385/j.cnki.issn.1004-4523.2024.05.004
1 概 述
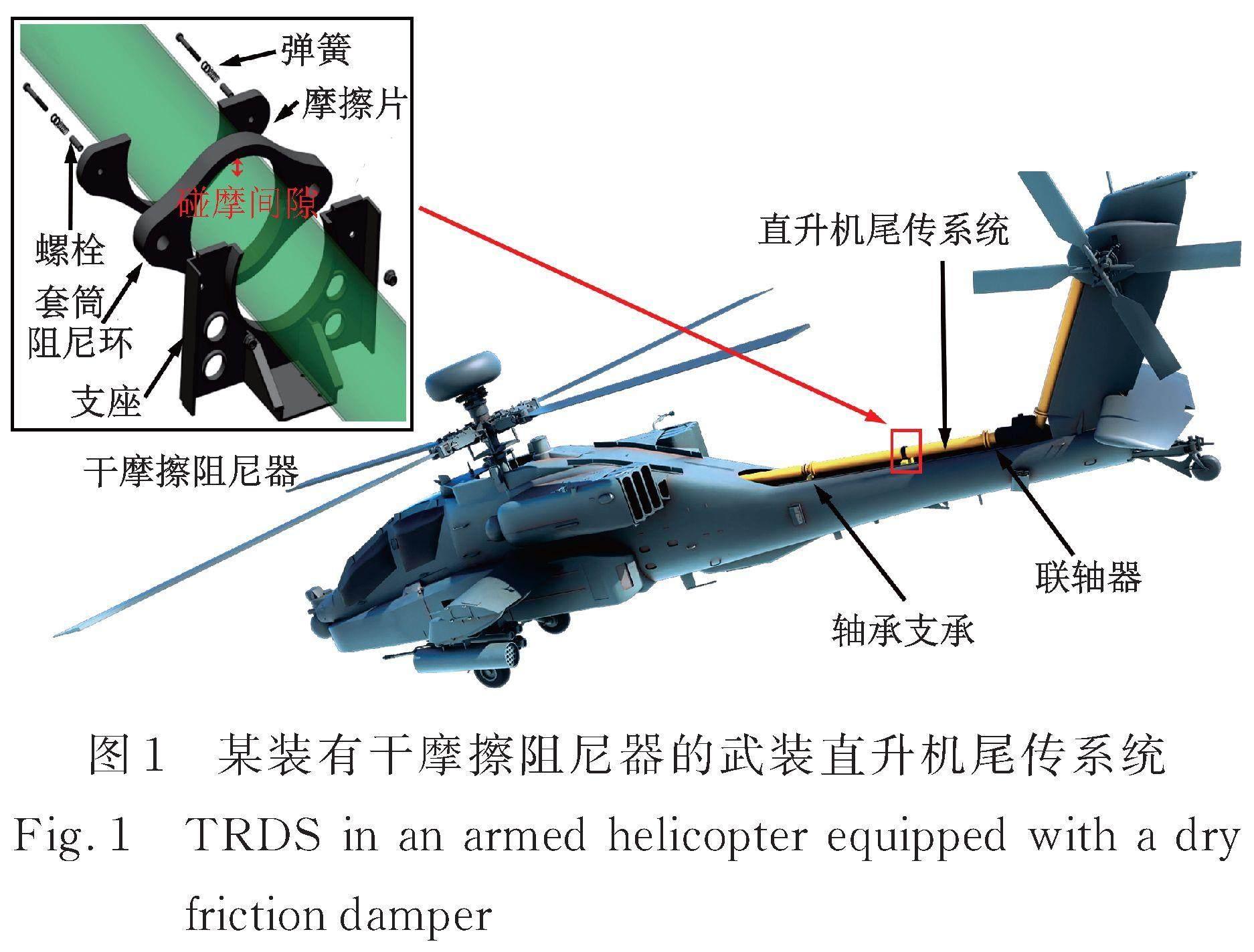
直升机尾传动轴是直升机传动系统的重要组成部分,如图1所示,主要用于传递主减速器的尾输出动力到尾桨[1]。传动轴有两种设计方案[2]:一是亚临界设计,传动轴的最大工作转速低于一阶临界转速;二是超临界设计,实际运行中传动轴的转速在一阶临界转速甚至二阶临界转速之上。传统的亚临界设计在启动或停止过程中传动轴无需跨临界转速,因此动力学设计较为简单[3]。相比之下,超临界设计下传动轴的跨度更大,这进一步减少了支承数量,使得传动轴结构简单,重量和成本都更低,且可靠性更高。随着直升机技术的发展,安全性、可靠性和运营成本的优化成为直升机未来的发展趋势[4]。亚临界设计因较高的成本及较低的功重比逐渐不能满足直升机发展需求,使得超临界设计逐渐成为传动轴设计的主流。由于传动轴存在不平衡量,系统在跨临界转速时传动轴会受到偏心激励,产生剧烈的径向振动,甚至导致其破坏失效,这一问题严重影响传动轴乃至直升机传动系统的寿命和安全性[5]。因此,本文针对直升机超临界尾传动轴设计方案跨临界过程产生剧烈振动的问题,开展跨临界减振技术研究,具有重要意义。
直升机尾传动轴上应用的减振器主要有两种。一种是支承减振器,安装在传动轴系的轴承与轴承座之间,通过自身阻尼实现对传动轴的减振,但由于超临界设计尾传动轴的跨度较大,这种方法减振效果并不十分明显[6]。
另一种是干摩擦阻尼器,安装在轴跨中间,如图1所示。干摩擦阻尼器由支座、阻尼环、摩擦片、螺栓套筒、弹簧及螺栓螺母等组合构成。摩擦片通过螺栓、螺栓套筒和弹簧完全固定在支座上。由于阻尼环安装孔相对于摩擦片安装孔较大,并未和螺栓套筒配合,因而阻尼环是相对浮动的。通过调节螺栓预紧力可以控制阻尼环的最大侧向干摩擦力,同时阻尼环和传动轴在安装时留有一定的初始碰摩间隙。当传动轴的振幅提高,传动轴位移大小超过碰摩间隙值时会造成传动轴对阻尼环的碰摩冲击,这种冲击会使阻尼环产生运动的趋势。此时由于阻尼环和摩擦片接触,使得阻尼环受到自摩擦片的侧向干摩擦力作用。
传动轴和阻尼环间的碰摩会产生各种碰摩响应类型,而确定系统参数空间中各碰摩响应之间边界条件及其稳定区域,厘清不同系统参数对响应之间边界条件的影响效果,对直升机尾传系统的工程设计具有十分重要的参考价值。
传动轴和阻尼器之间的相互作用类似于转子/定子系统的碰摩冲击现象,该现象已有广泛的研究[7?8]。Ehrich[9]发现接触非线性转子在非平衡激励下的亚谐波、超谐波和混沌响应。许斌等[10]以转子/定子系统为对象,采用当量弹簧线性碰摩模型,进行了同步全周碰摩响应下运动分析,推导出同步全周碰摩解稳定性判据,给出稳定区判据近似表达式。Jiang等[11]对转子/定子系统产生反向涡动碰摩响应的现象进行机理分析,发现系统在转速达到负固有频率附近时发生共振并失稳是反向涡动响应形成的原因,并在此基础上使用多尺度法求解得出反向涡动响应的边界。Chen等[12]针对转子/定子系统的自由振动方程使用解析法推导出带有约束条件的非线性简正模态,并基于此预测了系统自激反向涡动的一些重要特性。Shang等[13]考虑了转子和定子交叉耦合效应的影响,分析了转子/定子系统同频全周碰摩响应解的稳定性,并讨论了不同系统参数平面下交叉耦合效应对其稳定性的影响。Bartha[14]指出,转子/定子系统避免产生反向涡动响应的方法之一是降低转子和定子之间的摩擦系数,并且若无法避免反向涡动,也可通过调整定子的动态特性以改变反向涡动频率,避免更大的危害。Shang等[15]深入研究了不同碰摩响应在系统参数空间下的共存类型及其与各参数的关系。Jiang等[16]在研究转子/定子系统模型反向涡动的响应特性的过程中,进一步考虑了转子和定子接触表面的摩擦和变形,发现反向涡动响应存在多个边界且边界特性由系统参数决定。Srivastava等[17]针对转子/定子系统中摩擦力的Heaviside函数使控制方程不连续的问题,提出使用平滑函数代替的方法,如此可有效地检测转子摩擦的起始和瞬时频率特性。
与传统四自由度的转子/定子系统相比,传动轴/阻尼器系统的碰摩现象是故意设计出来的,阻尼环必须与传动轴在跨临界过程中发生碰摩,以进行缓冲减振。为研究系统的振动特性,D?ygad?o等[18]基于有限元法的数学模型计算了传动轴/阻尼器系统在时域上的跨临界振动响应,并指出随着阻尼器参数的改变,传动轴的运动会出现混沌现象。?zaydin等[19?20]结合谐波平衡法和数值延拓法描述传动轴/阻尼器系统在频域中的非线性力学特性。然而,在他们的研究中,阻尼环的质量被忽略了,传动轴和阻尼环之间的相互作用力被理想化的碰摩力模型所描述。为了解决这个问题,Huang等[21]提出传动轴/阻尼器相互作用的碰摩模型,研究了带有弹性联轴器和干摩擦阻尼器的超临界直升机尾传动轴的动态特性;且进一步用解析法推导出发生碰摩冲击的边界和Hopf分叉的边界,并分析了摩擦系数、内部阻尼、悬架刚度和可变冲击刚度对各边界的影响[22]。Wang等[3, 5, 23]、宋立瑶等[24]基于直接时间域积分和时频变换谐波平衡法+数值延拓法两种手段对控制方程进行了求解,并借助Floquet理论进一步研究了系统在不同转速下分岔的稳定性,同时确定系统分岔点。
Huang等[22]以带有干摩擦阻尼器的传动轴为对象,对其全局响应边界使用解析法进行了推导,然而,该研究中并未考虑阻尼环所受摩擦片的侧向干摩擦力的影响。阻尼环和摩擦片之间的摩擦力会改变系统的控制方程,从而导致系统稳定性边界条件和碰摩响应特性发生变化。为探究阻尼环受摩擦力作用下的传动轴/阻尼器系统的各碰摩响应边界及物理量参数对系统在跨临界转速下响应稳定性的影响,本文以某带有干摩擦阻尼器的直升机单跨超临界尾传动轴为研究对象,使用解析法推导系统全局响应边界,并通过数值法进行验证。
2 系统物理模型及控制方程
本文研究对象是某装有干摩擦阻尼器的直升机单跨超临界尾传动轴,在常规工况下,其转速高于一阶临界转速。如图2所示,为抑制传动轴在跨一阶临界转速时的剧烈振动,在传动轴的中间安装了干摩擦阻尼器。本文假设传动轴两端支撑在理想轴承上,并将传动轴简化建模为Jeffcott转子,其具有有效刚度和有效阻尼。Jeffcott转子刚性盘位于传动轴的中点,其质量为,偏心距离为,以角速度旋转。干摩擦阻尼器的阻尼环与传动轴同轴心安装,质量为![]() ,初始碰摩间隙为
,初始碰摩间隙为![]() 。当刚性盘的振动幅度超过初始碰摩间隙时,刚性盘会冲击阻尼环,产生碰摩冲击力的径向分量
。当刚性盘的振动幅度超过初始碰摩间隙时,刚性盘会冲击阻尼环,产生碰摩冲击力的径向分量![]() 。与转子/定子系统碰摩相同,刚性盘和阻尼环碰摩后产生的碰摩冲击力的切向分量
。与转子/定子系统碰摩相同,刚性盘和阻尼环碰摩后产生的碰摩冲击力的切向分量![]() 作用于接触点。
作用于接触点。![]() 的方向取决于传动轴和阻尼环接触点处的线速度
的方向取决于传动轴和阻尼环接触点处的线速度![]() 。碰摩后阻尼环也受到摩擦片侧向干摩擦力
。碰摩后阻尼环也受到摩擦片侧向干摩擦力![]() 的作用,从而对系统的跨临界振动进行抑制。最后,假设系统随时间变量
的作用,从而对系统的跨临界振动进行抑制。最后,假设系统随时间变量![]() 进行变化。
进行变化。
在不考虑系统陀螺效应的情况下,依据上文假定模型,系统的控制方程如下:
式中 rs = [ ys zs ]T,rd = [ yd zd ]T分别表示传动轴和阻尼环的几何中心的位移, 其中ys,zs,yd,zd 分别表示传动轴与阻尼环在y 向、z 向的位移距离值;上标号“?”表示对时间变量t 的微分;P 为碰摩冲击力,包括冲击力径向分量Pn 和冲去力切向分量Pt;kr 表示阻尼环作用于传动轴的刚度值;Fe 表示传动轴偏心激励力;Ff 表示摩擦片施加在阻尼环上的侧向干摩擦力;Fmax 为侧向干摩擦力下的最大静摩擦力值;Θ 为Heaveside 函数,当| rs - rd | ?δ0 时Θ = 1,当| rs - rd |< δ0 时Θ = 0;sign (vrel ) 为传动轴和阻尼环接触点的相对速度正负,系统在碰摩过程中传动轴和阻尼环间的切向摩擦力方向始终与接触点的相对速度方向相反。
式(1)的有效性已通过试验进行验证[5],为简化后续解析法推导过程,将式(1)无量纲化,将式(1)两端同时除以系数ks es,得[25]:
3 碰摩响应边界求解
3.1 典型碰摩响应特征
根据某型直升机的工程参数,本文所选传动轴/阻尼器系统物理量参数如表1所示[5]。
为清晰地了解传动轴/阻尼器系统在加速和减速过程中响应的类型及其转速范围,取表1的参数为系统扫频过程的参数,使用数值法对式(2)控制方程进行加减速过程的仿真。在扫频仿真过程中,以上一个激励频率下系统响应的末状态作为下一个激励频率下系统的初状态,以0.01作为扫频步长,分别将从0增速到2和从2减速到0作为正向和反向的扫频过程。在每一个激励频率下,运行1000个激励周期以保证传动轴运行到稳定状态,并取后50个周期作为该激励频率下系统的稳态响应结果,截取后50个周期每个周期一个点以绘制传动轴及阻尼环的扫频响应分岔图;同时选取每个激励频率下最大幅值绘制传动轴及阻尼环的无量纲幅值线,如图3所示。
参考图3,无论正向还是反向,扫频过程中系统响应可以分为四个阶段:Ⅰ,Ⅱ,Ⅲ,Ⅳ[5]。分别求解正向扫频下![]() =0.8,
=0.8,![]() =0.98,
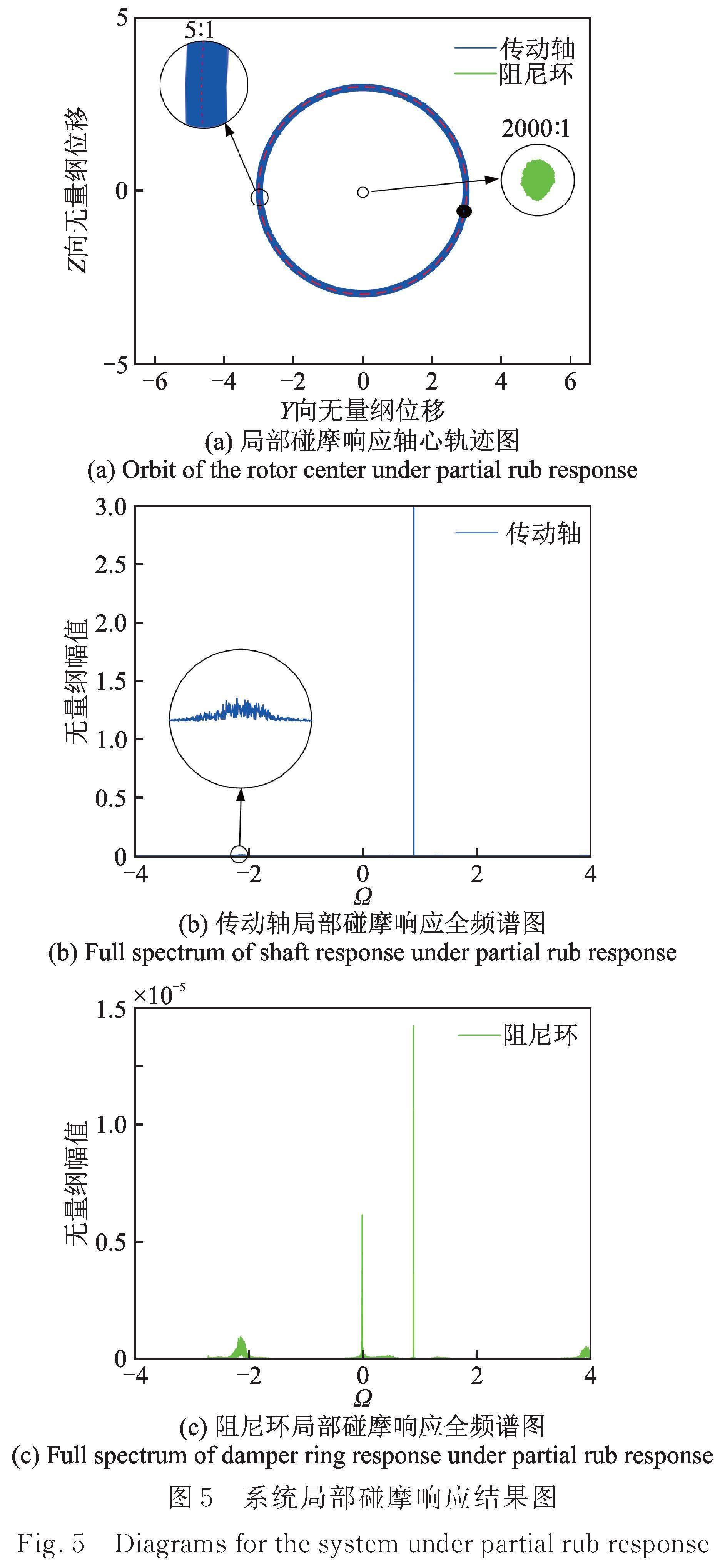
=0.98,![]() =1.2所对应响应类型的轴心轨迹图,传动轴及阻尼环全频谱图如图4~6所示,其中红线表示系统的初始碰摩间隙值。
=1.2所对应响应类型的轴心轨迹图,传动轴及阻尼环全频谱图如图4~6所示,其中红线表示系统的初始碰摩间隙值。
综上所述,系统在不同的参数条件下,会存在:(a)无碰摩响应;(b)局部碰摩响应;(c)同频全周碰摩响应。图5中传动轴、阻尼环含有负频率的成分,说明出现局部碰摩响应后,系统有轻微的反转趋势[26]。下文将分别求解此三种响应相互之间的边界条件。
3.2 无碰摩响应边界求解
无碰摩响应边界为系统在扫频过程中从无碰摩响应进入碰摩后各响应类型的边界条件。当系统处于无碰摩响应状态时,根据式(2)系统控制方程,可得传动轴的单周期线性解:
(5)
从式(5)的零解可得到两个实根:
式中![]() 为求解的无碰摩响应低转速边界,
为求解的无碰摩响应低转速边界,![]() 为求解的无碰摩响应高转速边界。
为求解的无碰摩响应高转速边界。
3.3 同频全周碰摩响应边界求解
当阻尼环与传动轴发生碰摩后,其响应类型分为两种:一种是系统做单周期运动的同频全周碰摩响应;另一种是系统做准周期运动的局部碰摩响应。所定义同频全周碰摩响应边界为系统在扫频过程中,同频全周碰摩响应发生失稳的边界。基于此,本文通过假定系统处于同频全周碰摩响应单周期运动的解,再分析其稳定性边界,进而确定同频全周碰摩响应的失稳边界。
为方便求解系统在同频全周碰摩响应的解析解,利用坐标变换将系统从惯性坐标转换到旋转坐标下。此时阻尼环与传动轴接触,满足![]() ,假设如下变换:
,假设如下变换:
式中![]() 为假定系统处于同频全周碰摩响应下的传动轴位移距离值,
为假定系统处于同频全周碰摩响应下的传动轴位移距离值,![]() 为假定系统处于同频全周碰摩响应下的阻尼环位移距离值。
为假定系统处于同频全周碰摩响应下的阻尼环位移距离值。
将式(7)旋转坐标变换的结果代入式(2),同时考虑![]() ,可得:
,可得:
为方便推导同频全周碰摩响应的响应解,将碰摩力![]()
改写为如下形式[27]:
当![]() ,
,![]() ,
,![]() 和
和![]() 时,可得系统的稳态解:
时,可得系统的稳态解:
同频全周碰摩响应下传动轴和阻尼环位移的矢量解形式![]() 和
和![]() 可求解得出,具体方法见附录。
可求解得出,具体方法见附录。
通过解出同频全周碰摩响应传动轴和阻尼环的稳态响应解,可进一步求解同频全周碰摩响应的失稳边界条件。由式(8)可得传动轴和阻尼环的加速度为:
将系统的响应振幅矢量分为![]() 方向和
方向和![]() 方向:
方向:![]() ,
,![]() 。式(11)可表示为一阶微分方程形式:
。式(11)可表示为一阶微分方程形式:
定义系统旋转坐标系下的状态向量为:
将式(12)改写为如下形式:
依据所求解矢量形式的同频全周碰摩的稳态响应解![]() 和
和![]() ,确定系统旋转坐标系下的稳态不动点:
,确定系统旋转坐标系下的稳态不动点:
基于此不动点对式(14)非线性项进行线性化[15],得到系统的Jacobian矩阵:
系统的Jacobian矩阵的特征值由下式求解:
采用Routh?Hurwitz稳定性判据对系统进行判别[28],系统的特征方程为:
(18)
特征方程的各项系数受同频全周响应解的非线性项的影响,当系统特征方程的八个特征值的实部都小于零时,系统在运动状态下是稳定的,否则该稳态响应解是不稳定的,由此可以确定同频全周碰摩响应边界。
4 边界条件验证及各参数的影响
4.1 边界条件验证
上文推导出系统各碰摩类型的边界解析解,本节将使用数值积分方法对这些边界计算结果进行验证。
同样方法可验证同频全周碰摩响应边界,依据表1物理量参数,使用式(23)分析系统Jacobian矩阵特征值实部均小于0的情况,如图7(b)所示。图7(b)中两条黄线所表示的同频碰摩响应边界(![]() ,
,![]() )内系统属于同频全周碰摩响应的稳定区域。为验证该解析解的准确性,选取系统摩擦系数
)内系统属于同频全周碰摩响应的稳定区域。为验证该解析解的准确性,选取系统摩擦系数![]() 在0.02~0.3的15组数据进行正向扫频分析,当系统进入同频全周碰摩响应后继续扫频;当系统从同频全周碰摩响应转为无碰摩响应时,记为系统在正向扫频下的同频全周碰摩响应边界。同样,反向扫频时则取系统从单周期运动转为准周期运动时为同频全周碰摩响应边界,如图7(b)所示。结果表明,使用数值法所求解系统同频全周碰摩响应变化的边界与解析法所求解边界基本相同,从而证明上文解析法求解同频全周碰摩响应边界的正确性。
在0.02~0.3的15组数据进行正向扫频分析,当系统进入同频全周碰摩响应后继续扫频;当系统从同频全周碰摩响应转为无碰摩响应时,记为系统在正向扫频下的同频全周碰摩响应边界。同样,反向扫频时则取系统从单周期运动转为准周期运动时为同频全周碰摩响应边界,如图7(b)所示。结果表明,使用数值法所求解系统同频全周碰摩响应变化的边界与解析法所求解边界基本相同,从而证明上文解析法求解同频全周碰摩响应边界的正确性。
下文将讨论系统参数对所验证碰摩响应边界的影响,在传动轴已知的情况下为干摩擦阻尼器的设计提供参考。在七个无量纲系统参数(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )中,考虑到系统无量纲转速
)中,考虑到系统无量纲转速![]() 是响应边界的求解变量,并且
是响应边界的求解变量,并且![]() 为传动轴的固有参数,而
为传动轴的固有参数,而![]() 则对响应边界影响不大,故本文集中分析系统参数
则对响应边界影响不大,故本文集中分析系统参数![]() ,
,![]() ,
,![]() 与
与![]() 对系统响应边界的影响。
对系统响应边界的影响。
4.2 摩擦系数影响分析
基于表1物理量参数,系统在![]() 参数平面下的碰摩响应变化如图8所示。根据所求解的结果,无碰摩响应边界不受摩擦系数
参数平面下的碰摩响应变化如图8所示。根据所求解的结果,无碰摩响应边界不受摩擦系数![]() 的影响,在
的影响,在![]() 参数平面上表现为两条直线。当系统满足转速
参数平面上表现为两条直线。当系统满足转速![]() 的条件下,系统存在无碰摩响应。考虑到响应类型在相同参数条件下存在共存现象,因而这不能决定在系统符合转速的条件下,只存在无碰摩响应类型[27]。
的条件下,系统存在无碰摩响应。考虑到响应类型在相同参数条件下存在共存现象,因而这不能决定在系统符合转速的条件下,只存在无碰摩响应类型[27]。
系统正向扫频过程如图8(a)所示,首先经过![]() 系统进入碰摩状态,此时系统处于局部碰摩响应状态。数值仿真结果表明,随着转速的提高,系统越来越接近单周期运动的同时,阻尼环的位移大小逐渐增大;随着系统转速持续增加,系统进入同频全周碰摩响应区域,其边界与
系统进入碰摩状态,此时系统处于局部碰摩响应状态。数值仿真结果表明,随着转速的提高,系统越来越接近单周期运动的同时,阻尼环的位移大小逐渐增大;随着系统转速持续增加,系统进入同频全周碰摩响应区域,其边界与![]() 重合。系统同频全周碰摩响应正向扫频下的稳定性将持续到
重合。系统同频全周碰摩响应正向扫频下的稳定性将持续到![]() 线。当系统达到
线。当系统达到![]() 后,同频全周碰摩响应失稳,此时阻尼环回归零点,传动轴发生了“跳跃”现象,脱离了与阻尼环的碰摩,系统转为无碰摩响应状态。
后,同频全周碰摩响应失稳,此时阻尼环回归零点,传动轴发生了“跳跃”现象,脱离了与阻尼环的碰摩,系统转为无碰摩响应状态。
系统进行反向扫频时,碰摩响应变化如图8(b)所示。当系统转速降低到![]() 时发生碰摩,此时数值仿真结果表明系统处于同频全周碰摩响应状态。系统转速进而降低到
时发生碰摩,此时数值仿真结果表明系统处于同频全周碰摩响应状态。系统转速进而降低到![]() 后脱离同频全周碰摩响应的稳定区域,系统转为局部碰摩响应状态。最后,随着转速降低阻尼环回归零点,并且传动轴逐渐转为单周期运动,仿真结果表明转速进一步降低后阻尼环和传动轴脱离接触,系统回归无碰摩响应状态,其边界也与
后脱离同频全周碰摩响应的稳定区域,系统转为局部碰摩响应状态。最后,随着转速降低阻尼环回归零点,并且传动轴逐渐转为单周期运动,仿真结果表明转速进一步降低后阻尼环和传动轴脱离接触,系统回归无碰摩响应状态,其边界也与![]() 重合。
重合。
系统的同频全周碰摩响应稳定性区域受到摩擦系数![]() 的影响,随着
的影响,随着![]() 的增加,稳定性区域逐渐减少。相比
的增加,稳定性区域逐渐减少。相比![]() ,当
,当![]() 时同频全周碰摩响应的稳定性区域减少了16.32%。考虑到局部碰摩响应下传动轴等部件会受到冲击,进而造成更严重的损伤[27],因此系统所设计的
时同频全周碰摩响应的稳定性区域减少了16.32%。考虑到局部碰摩响应下传动轴等部件会受到冲击,进而造成更严重的损伤[27],因此系统所设计的![]() 不宜过高。
不宜过高。
4.3 初始碰摩间隙影响分析
设传动轴和阻尼环初始碰摩间隙![]() 为变量,其余物理量参数参考表1。使用式(5)和式(22),可得
为变量,其余物理量参数参考表1。使用式(5)和式(22),可得![]() 参数平面下的无碰摩响应和同频全周碰摩响应的边界图,如图9所示。所求解无碰摩响应边界在
参数平面下的无碰摩响应和同频全周碰摩响应的边界图,如图9所示。所求解无碰摩响应边界在![]() 参数平面表现为一条在系统临界转速处有波峰的线。当
参数平面表现为一条在系统临界转速处有波峰的线。当![]() 时为
时为![]() ;当
;当![]() 时为
时为![]() 。同样,所求解同频全周碰摩响应边界也根据低转速和高转速分为
。同样,所求解同频全周碰摩响应边界也根据低转速和高转速分为![]() 与
与![]() 。
。
依据所求解的两个边界,可得到系统在![]() 范围时,不同碰摩间隙值下系统正向及反向扫频时碰摩响应的变化,如图10所示。当系统正向扫频时,首先通过
范围时,不同碰摩间隙值下系统正向及反向扫频时碰摩响应的变化,如图10所示。当系统正向扫频时,首先通过![]() 从无碰摩响应状态进入局部碰摩响应状态。然后通过数值仿真,结果表明,当
从无碰摩响应状态进入局部碰摩响应状态。然后通过数值仿真,结果表明,当![]() <21.14,随着转速的增加,系统碰摩响应类型随后会变为同频全周碰摩响应,在进一步增加转速时,同频全周碰摩响应会发生失稳,系统最终脱离碰摩进入无碰摩响应状态。另一方面,当
<21.14,随着转速的增加,系统碰摩响应类型随后会变为同频全周碰摩响应,在进一步增加转速时,同频全周碰摩响应会发生失稳,系统最终脱离碰摩进入无碰摩响应状态。另一方面,当![]() >21.14时,随着转速增加局部碰摩会直接脱离接触进入无碰摩运动,其边界记为
>21.14时,随着转速增加局部碰摩会直接脱离接触进入无碰摩运动,其边界记为![]() 。在
。在![]() 边界处,阻尼环的位移不为0,这导致相比于在反向扫频下的发生碰摩的
边界处,阻尼环的位移不为0,这导致相比于在反向扫频下的发生碰摩的![]() 边界,正向扫频下通过
边界,正向扫频下通过![]() 脱离碰摩会更为困难,因此在相同
脱离碰摩会更为困难,因此在相同![]() 值下
值下![]() 要比
要比![]() 偏向高转速区。
偏向高转速区。
反向扫频下系统通过![]() 发生碰摩,系统从无碰摩响应状态转为局部碰摩响应状态或者同频全周碰摩响应状态。与正向扫频不同的是,反向扫频下系统碰摩脱离边界处的阻尼环的位移接近于0,且传动轴符合单周期运动的趋势,这使得反向扫频下系统脱离碰摩的边界与
发生碰摩,系统从无碰摩响应状态转为局部碰摩响应状态或者同频全周碰摩响应状态。与正向扫频不同的是,反向扫频下系统碰摩脱离边界处的阻尼环的位移接近于0,且传动轴符合单周期运动的趋势,这使得反向扫频下系统脱离碰摩的边界与![]() 完全相同。
完全相同。
系统在不同初始碰摩间隙下正向及反向扫频过程中的碰摩响应变化如表2所示。由表2可知,所求解系统的无碰摩响应边界和同频全周碰摩响应边界均受初始碰摩间隙的影响。当系统![]() 值超过25时,阻尼环与传动轴始终不发生碰摩,系统将一直处于无碰摩响应状态,所安装干摩擦阻尼器没有起到抑振的作用。当系统满足21.14<
值超过25时,阻尼环与传动轴始终不发生碰摩,系统将一直处于无碰摩响应状态,所安装干摩擦阻尼器没有起到抑振的作用。当系统满足21.14<![]() <25的情况下,系统在碰摩过程中只会产生局部碰摩响应。随着
<25的情况下,系统在碰摩过程中只会产生局部碰摩响应。随着![]() 的减少系统同频全周碰摩响应的稳定性区域出现并逐渐增加。
的减少系统同频全周碰摩响应的稳定性区域出现并逐渐增加。
4.4 最大静摩擦力影响分析
假定最大静摩擦力![]() 为变量,其余物理量参数参考表1。由式(5)和式(22)可得
为变量,其余物理量参数参考表1。由式(5)和式(22)可得![]() 参数平面下的无碰摩响应和同频全周碰摩响应的边界图如图11所示。与
参数平面下的无碰摩响应和同频全周碰摩响应的边界图如图11所示。与![]() 参数平面相同,所求解无碰摩响应边界也不受
参数平面相同,所求解无碰摩响应边界也不受![]() 影响,在
影响,在![]() 参数平面表现为两条直线
参数平面表现为两条直线![]() 和
和![]() 。同频全周碰摩响应边界在
。同频全周碰摩响应边界在![]() 参数平面上表现为两条抛物线,随
参数平面上表现为两条抛物线,随![]() 的增大而趋向于高转速区,分别为
的增大而趋向于高转速区,分别为![]() ,
,![]() 。
。
系统在![]() 参数平面的正向及反向扫频下碰摩响应变化如图12所示,系统在不同
参数平面的正向及反向扫频下碰摩响应变化如图12所示,系统在不同![]() 值下正向及反向扫频过程的碰摩响应类型变化如表3所示。在正向扫频过程中,随着
值下正向及反向扫频过程的碰摩响应类型变化如表3所示。在正向扫频过程中,随着![]() 的增加,系统从无碰摩响应状态通过
的增加,系统从无碰摩响应状态通过![]() 时便开始发生碰摩,产生局部碰摩响应。根据数值仿真的计算结果,在
时便开始发生碰摩,产生局部碰摩响应。根据数值仿真的计算结果,在![]() <8的范围内,系统随着转速的提高不会从局部碰摩响应状态内脱离碰摩,而必定会转为同频全周碰摩响应状态,然后再越过
<8的范围内,系统随着转速的提高不会从局部碰摩响应状态内脱离碰摩,而必定会转为同频全周碰摩响应状态,然后再越过![]() 发生同频全周碰摩响应的失稳而脱离碰摩。
发生同频全周碰摩响应的失稳而脱离碰摩。
在反向扫频的过程中,系统会通过![]() 开始碰摩。当
开始碰摩。当![]() <3.03时系统会产生同频全周碰摩响应状态,然后经过
<3.03时系统会产生同频全周碰摩响应状态,然后经过![]() 因同频全周碰摩响应失稳而转为局部碰摩响应状态,随着减速阻尼环位移逐渐归零,仿真表明系统在经过
因同频全周碰摩响应失稳而转为局部碰摩响应状态,随着减速阻尼环位移逐渐归零,仿真表明系统在经过![]() 时变脱离碰摩;当
时变脱离碰摩;当![]() >3.03时,系统通过
>3.03时,系统通过![]() 会直接进入局部碰摩响应状态,再进而脱离碰摩。
会直接进入局部碰摩响应状态,再进而脱离碰摩。
由图12和表3可知,系统在正向扫频下,随着![]() 的增大进入同频全周碰摩响应的边界会转移向高转速区。系统在反向扫频下,当
的增大进入同频全周碰摩响应的边界会转移向高转速区。系统在反向扫频下,当![]() <3.03时,随着
<3.03时,随着![]() 提高同频全周碰摩响应稳定性区域会减少,这导致局部碰摩响应范围的增大;当
提高同频全周碰摩响应稳定性区域会减少,这导致局部碰摩响应范围的增大;当![]() >3.03时,系统不会出现同频全周碰摩响应。
>3.03时,系统不会出现同频全周碰摩响应。
4.5 传动轴等效刚度影响分析
假定传动轴等效刚度![]() 为变量,其余物理量参数参考表1。由式(5)和式(22)可得
为变量,其余物理量参数参考表1。由式(5)和式(22)可得![]() 参数平面下的无碰摩响应和同频全周碰摩响应的边界图如图11所示。所求解无碰摩响应边界不受
参数平面下的无碰摩响应和同频全周碰摩响应的边界图如图11所示。所求解无碰摩响应边界不受![]() 影响,在
影响,在![]() 参数平面表现为两条直线
参数平面表现为两条直线![]() ,
,![]() 。同频全周碰摩响应边界也存在两条,分别为
。同频全周碰摩响应边界也存在两条,分别为![]() ,
,![]() 。在
。在![]() 较小情况下,随
较小情况下,随![]() 的增大同频全周碰摩响应边界趋向于高转速区;在
的增大同频全周碰摩响应边界趋向于高转速区;在![]() 值较大情况下,同频全周碰摩响应边界将几乎不会随
值较大情况下,同频全周碰摩响应边界将几乎不会随![]() 改变。
改变。![]()
系统正向扫频过程如图14(a)所示,在正向扫频过程中,随着![]() 的增加,系统从无碰摩响应状态通过
的增加,系统从无碰摩响应状态通过![]() 时便开始发生碰摩,产生局部碰摩响应。根据数值仿真的计算结果,在
时便开始发生碰摩,产生局部碰摩响应。根据数值仿真的计算结果,在![]() <0.11的情况下,随着系统转速增加系统不会进入同频全周碰摩响应而直接脱离碰摩。当0.11<
<0.11的情况下,随着系统转速增加系统不会进入同频全周碰摩响应而直接脱离碰摩。当0.11<![]() <0.52时,系统会在脱离碰摩前进入同频全周碰摩响应区域,但是随后经过
<0.52时,系统会在脱离碰摩前进入同频全周碰摩响应区域,但是随后经过![]() 失稳回到局部碰摩响应状态,最后脱离碰摩。在0.52<
失稳回到局部碰摩响应状态,最后脱离碰摩。在0.52<![]() 情况下,数值仿真结果表明,系统发生碰摩后会从局部碰摩响应状态转为同频全周碰摩响应状态并进而经过
情况下,数值仿真结果表明,系统发生碰摩后会从局部碰摩响应状态转为同频全周碰摩响应状态并进而经过![]() 后脱离碰摩。
后脱离碰摩。
系统进行反向扫频时,碰摩响应变化如图14(b)所示。当系统转速降低到![]() 时发生碰摩。当
时发生碰摩。当![]() <0.11时,系统处于局部碰摩响应状态,随着转速的降低系统转轴和阻尼环逐渐脱离接触。当 0.11<
<0.11时,系统处于局部碰摩响应状态,随着转速的降低系统转轴和阻尼环逐渐脱离接触。当 0.11<![]() <0.52时,系统响应类型变化与正向扫频相同,会从局部碰摩响应状态进入同频全周碰摩响应状态,随后经过
<0.52时,系统响应类型变化与正向扫频相同,会从局部碰摩响应状态进入同频全周碰摩响应状态,随后经过![]() 后失稳回归局部碰摩响应状态,最后随着速度的减少脱离碰摩。当0.52<
后失稳回归局部碰摩响应状态,最后随着速度的减少脱离碰摩。当0.52<![]() 时,系统处于同频全周碰摩响应状态,经过
时,系统处于同频全周碰摩响应状态,经过![]() 后变为局部碰摩响应状态,然后随着转速降低传动轴的位移逐渐降低最终与阻尼环脱离接触。
后变为局部碰摩响应状态,然后随着转速降低传动轴的位移逐渐降低最终与阻尼环脱离接触。
5 结 论
本文针对某带有干摩擦阻尼器的直升机单跨超临界尾传动轴的碰摩现象,通过使用解析方法推导出无碰摩响应边界和同频全周碰摩响应边界,并使用Runge?Kutta 法进行了验证,最后讨论了![]() ,
,![]() ,
,![]() 和
和![]() 对边界条件的影响,得到以下结论:
对边界条件的影响,得到以下结论:
(1)传动轴/干摩擦阻尼器系统的跨临界转速过程的典型响应类型可以分为三种,分别为无碰摩响应、局部碰摩响应以及同频全周碰摩响应,且各响应类型的边界与系统的物理量参数密切相关。
(2)依据无碰摩响应下发生碰摩的边界条件,求解了系统无碰摩响应的边界。证明![]() ,
,![]() 和
和![]() 不会对其产生影响,在
不会对其产生影响,在![]() 平面和
平面和![]() 参数平面上表现为两条垂线。所求解无碰摩响应边界受
参数平面上表现为两条垂线。所求解无碰摩响应边界受![]() 影响,随
影响,随![]() 增大,无碰摩响应边界向临界转速收缩。
增大,无碰摩响应边界向临界转速收缩。
(3)基于Routh?Hurwitz稳定性判据,针对系统同频全周碰摩响应求解其稳定性边界。同频全周碰摩响应边界受![]() 与
与![]() 影响显著。随
影响显著。随![]() 增大,同频全周碰摩响应会收缩进而消失。随
增大,同频全周碰摩响应会收缩进而消失。随![]() 与
与![]() 的增大,同频全周碰摩响应边界趋于转到高转速区。同频全周碰摩响应稳定性边界也受
的增大,同频全周碰摩响应边界趋于转到高转速区。同频全周碰摩响应稳定性边界也受![]() 影响,随其增大区域会略微压缩。
影响,随其增大区域会略微压缩。
现有的工作在局部碰摩响应边界求解上依然使用数值方法,而如何假定系统局部碰摩响应解的形式进而通过解析方法求解其边界条件仍需进一步探讨。
参考文献:
[1] Zhu H M, Chen W F, Zhu R P, et al. Modeling and dynamic analysis of spiral bevel gear coupled system of intermediate and tail gearboxes in a helicopter[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2021, 235(22): 5975-5993.
[2] Song L Y, Chen B, Li B, et al. Nonlinear vibration response of a helicopter supercritical tail rotor drive shaft equipped with a dry friction damper[J]. Journal of Intelligent Manufacturing and Special Equipment, 2022,3(2):173-191.
[3] Wang D, Song L Y, Cao P, et al. Nonlinear modelling and parameter influence of supercritical transmission shaft with dry friction damper[J]. International Journal of Mechanics and Materials in Design, 2023, 19: 223-240.
[4] Samuel P D, Pines D J. A review of vibration-based techniques for helicopter transmission diagnostics[J]. Journal of Sound and Vibration, 2005, 282(1-2): 475-508.
[5] Wang D, Song L Y, Zhu R P, et al. Nonlinear dynamics and stability analysis of dry friction damper for supercritical transmission shaft[J]. Nonlinear Dynamics, 2022,110: 3135?3149.
[6] Liu S B, Yang B G. Optimal placement of water-lubricated rubber bearings for vibration reduction of flexible multistage rotor systems[J]. Journal of Sound and Vibration, 2017, 407: 332-349.
[7] Srivastava A K, Tiwari M, Singh A. Identification of rotor-stator rub and dependence of dry whip boundary on rotor parameters[J]. Mechanical Systems and Signal Processing, 2021, 159: 107845.
[8] Prabith K, Krishna I R P. The numerical modeling of rotor?stator rubbing in rotating machinery: a comprehensive review[J]. Nonlinear Dynamics, 2020, 101(2): 1317-1363.
[9] Ehrich F. Observations of subcritical superharmonic and chaotic response in rotordynamics[J]. Journal of Vibration and Acoustics,1992, 114(1): 93-100.
[10] 许斌,徐尉南,张文.单盘转子的同步全周碰摩及其稳定性分析[J]. 复旦学报(自然科学版), 2006, 45(2): 148-154.
XU Bin, XU Weinan, ZHANG Wen. Study of synchronous full annular rub of Jeffcott rotor and its dynamic stability[J]. Journal of Fudan University (Natural Science), 2006, 45(2): 148-154.
[11] Jiang J, Ulbrich H. The physical reason and the analytical condition for the onset of dry whip in rotor-to-stator contact systems[J].Journal of Vibration and Acoustics,2005, 127(6): 594-603.
[12] Chen Y H, Jiang J. Determination of nonlinear normal modes of a planar nonlinear system with a constraint condition[J]. Journal of Sound and Vibration, 2013, 332(20): 5151-5161.
[13] Shang Z Y, Jiang J, Hong L. The influence of the cross-coupling effects on the dynamics of rotor/stator rubbing[C]//Dynamical Systems: Discontinuity, Stochasticity and Time-Delay. New York: Springer, 2010: 121-132.
[14] Bartha A R. Dry friction backward whirl of rotors[D]. Zurich: Swiss Federal Institute of Technology, 2000.
[15] Shang Z Y, Jiang J, Hong L. The global responses characteristics of a rotor/stator rubbing system with dry friction effects[J]. Journal of Sound and Vibration, 2011, 330(10): 2150-2160.
[16] Jiang J, Shang Z Y, Hong L. Characteristics of dry friction backward whirl—a self-excited oscillation in rotor-to-stator contact systems[J]. Science China Technological Sciences, 2010, 53: 674-683.
[17] Srivastava A K, Tiwari M, Singh A. Identification of rotor-stator rub and dependence of dry whip boundary on rotor parameters[J]. Mechanical Systems and Signal Processing, 2021, 159: 107845.
[18] D?ygad?o Z, Perkowski W. Research on dynamics of a supercritical propulsion shaft equipped with a dry friction damper[J]. Aircraft Engineering and Aerospace Technology, 2002, 74(5): 447-454.
[19] ?zaydin O. Vibration reduction of helicopter tail shaft by using dry friction dampers[D]. Ankara: Middle East Technical University, 2017.
[20] ?zaydin O, Cigeroglu E. Effect of dry friction damping on the dynamic response of helicopter tail shaft[C]// Rotating Machinery, Hybrid Test Methods, Vibro-Acoustics & Laser Vibrometry, Volume 8: Proceedings of the 35th IMAC, A Conference and Exposition on Structural Dynamics 2017. Springer International Publishing, 2017: 23-30.
[21] Huang Z H, Tan J P, Liu C L, et al. Dynamic characteristics of a segmented supercritical driveline with flexible couplings and dry friction dampers[J]. Symmetry, 2021, 13(2): 281.
[22] Huang Z H, Tan J P, Liu C L, et al. All-round responses and boundaries of a shaft and dry friction damper assembly[J]. International Journal of Non-Linear Mechanics, 2022, 142: 103977.
[23] 王旦,宋立瑶,陈柏,等.直升机超临界尾传动轴限幅减振器非线性动力学特性研究[J]. 振动工程学报, 2023, 36(3): 593-605.
WANG Dan, SONG Liyao, CHEN Bai, et al. Study on the effect of installation location of dry friction damper for helicopter supercritical tail drive shaft[J]. Journal of Vibration Engineering, 2023, 36(3): 593-605.
[24] 宋立瑶,王旦,曹鹏, 等.直升机超临界尾轴限幅减振器安装位置研究[J]. 航空动力学报,2024, 39(6): 20220409.
SONG Liyao, WANG Dan, CAO Peng, et al. Study on the effect of installation location of dry friction damper for helicopter supercritical tail drive shaft[J]. Journal of Aerospace Power, 2024, 39(6): 20220409.
[25] Jiang J. Determination of the global responses characteristics of a piecewise smooth dynamical system with contact[J]. Nonlinear Dynamics, 2009, 57: 351-361.
[26] Kim T C, Rook T E, Singh R. Effect of smoothening functions on the frequency response of an oscillator with clearance non-linearity[J]. Journal of Sound and Vibration, 2003, 263(3): 665-678.
[27] Jiang J, Ulbrich H, Chavez A. Improvement of rotor performance under rubbing conditions through active auxiliary bearings[J]. International Journal of Non-Linear Mechanics, 2006, 41(8): 949-957.
[28] Nayfeh A H, Mook D T. Nonlinear Oscillations[M]. New York: John Wiley & Sons, Inc., 2008.
Boundary characterization of rub-impact response of a helicopter supercritical transmission shaft with a dry friction damper
Abstract: In pursuit of the ideal power-to-weight ratio, supercritical transmission shaft systems are increasingly used in the design of helicopter structures, which leads to the generation of violent vibrations driving through its critical speed. To suppress the excessive transcritical vibration, dry friction dampers are usually employed. In this study, a supercritical transmission shaft system with a dry friction damper is investigated. The governing equations are established and the boundary characteristics of various rub-impact responses of the system under eccentric excitation of the transmission shaft are analyzed. Firstly, the nonlinear governing equations of the damper/shaft system are constructed. Secondly, typical response characteristics are determined using frequency sweep, and the boundaries of impact occurrence and stability conditions for the synchronous full annular rub are solved using analytical methods. Finally, the derived response boundaries are verified by the Runge-Kutta method, and the relationship between the response boundaries and the system parameters is further explored.
Key words: supercritical transmission shaft;dry friction damper;rub-impact;response characteristics;stability analysis
将式(9)代入式(10)约去![]() ,并简化可得传动轴和阻尼环的矢量解为:
,并简化可得传动轴和阻尼环的矢量解为:
将式(A1)代入式(9),进而化简可得碰摩力![]() 的矢量解为:
的矢量解为:
由式(A2)可得碰摩力的大小![]() :
:
式中 系数a,b,c,d,e 和 f 为:
将式(A4)代入式(A2)可得碰摩力![]() 矢量解,进而代入式(A1)可得同频全周碰摩响应下传动轴和阻尼环位移的矢量解形式
矢量解,进而代入式(A1)可得同频全周碰摩响应下传动轴和阻尼环位移的矢量解形式![]() 和
和![]() 。
。
式(14)中![]() 为线性项的系数矩阵,定义为:
为线性项的系数矩阵,定义为:
式(A7)中![]() ,
,![]() ,
,![]() 和
和![]() 分别定义为:
分别定义为:
式(16)中的非线性项进行线性化后各项系数为:
