飞机刹车诱导颤振稳定性分析与减振设计

蒋伟 张明 尹乔之 朱鑫 胡晓航

摘要： 以飞机刹车装置为研究对象，对飞机刹车诱发振动问题进行了研究。针对飞机滑跑过程中的复杂制动环境对盘面摩擦特性影响，建立了考虑液压系统及盘面材料属性的刹车盘组非线性动力学分析模型，且为新材料技术的发展预留了模型接口。从实际工程应用价值出发，以机轮速度、液压系统等效阻尼、刹车盘面阻尼、盘面摩擦特性几类关键因素为控制变量，利用数值仿真与分岔理论等非线性分析手段研究了上述参数对系统稳定性的影响，并确定了使系统保持稳定的结构参数范围，方便对结构进行参数化快速分析设计。基于模型分析的结果，揭示了刹车振动产生的部分原因，从结构参数和刹车控制律两方面针对性的提出了对应的减振优化措施，进而形成了完整的飞机刹车诱导颤振的分析方法，为飞机制动器设计初期提供了理论参考依据。

关键词： 刹车诱导振动； 非线性模型； 分岔理论； 稳定性分析； 减振措施

中图分类号： V216.2+2    文献标志码： A    文章编号： 1004-4523（2024）05-0770-10

DOI：10.16385/j.cnki.issn.1004-4523.2024.05.005

引  言

在飞机着陆滑跑过程中，由于制动系统的频繁作用，会引发起落架系统出现不同程度的振动现象。依据振动频率的高低，可划分为低频起落架结构抖振和中高频的刹车装置颤振和尖叫［1］，其中抖振被定义为起落架支柱组件绕静态垂直支柱中心轴的前后循环运动［2］。在研究初期，部分学者认为中高频的振动幅度小、而忽视了这类振动对起落架结构的危害性［3］，所以国内外针对抖振方面的研究居多［4?7］，但实际上这类中高频振动会影响刹车装置及起落架的疲劳寿命，导致结构性破坏进而影响到飞行安全。此外，随着碳纤维增强和碳陶复合材料在刹车装置中的不断应用［8］，给早期研究中所建立的模型和研究方法带来了严峻的挑战，所以加强对中高频的刹车诱导振动相关问题研究就显得尤为重要。

飞机刹车振动是一个复杂的过程，振动的诱发往往不是由某一个因素引起的，而是受外部环境的扰动和内部结构的耦合、安装结构间隙、刹车盘的摩擦特性等的共同影响［9?10］，单一的零部件试验难以描述实际的飞机制动滑跑运动过程，而刹车系统性能的全尺寸真机地面滑跑实验成本过于高昂，建立系统模型进行仿真是一种成本低，效率高，具有一定参考价值的研究方案。早期对于刹车振动的仿真分析研究主要集中在车辆领域：一方面是利用有限元分析软件分析制动器部件的固有特性，LI等［11］通过对制动器的模态分析，研究外部激励频率对于刹车振动的影响；孟德建等［12?13］通过通风盘式制动器有限元模型，分析了该模型下的紧急制动工况应力场分布特征。另一方面是通过建立数学模型进行时域仿真分析， Wu等［14］应用数值模拟和复特征值分析法研究了中国高速列车的盘式制动系统的稳定性；Wang等［15］建立了一种考虑制动系统的新型车辆?轨道耦合动力学模型，从时域、频域、和相平面等方面验证了特殊制动条件下产生的强烈非线性特征。上述研究内容为飞机刹车振动问题提供了参考，但实际上两者制动环境存在较大差异，建模过程应依据各自特点有所侧重。

飞机和车辆刹车问题的差异点主要在于制动环境的不同，飞机着陆过程中刹车系统持续工作时间长且初始制动速度较高，盘面相对滑动速度或温度会在短时间内发生剧烈变化，进而引起摩擦系数的波动，所以针对飞机刹车问题的研究要特别注意盘面摩擦特性的建模处理。以往的研究中部分学者将制动摩擦系数设为恒定值来研究系统稳定性［16］，另一部分学者认为动态摩擦系数和盘面运动状态之间的关系对系统稳定性［17］有较大影响。对此采用了不同的摩擦模型，其中具有代表性的有： Leine等［18］建立了动静盘之间的交替摩擦模型，贾尚帅等［19］采用了 LuGre 模型，Meehan等［20?21］、Tan等［22］引用了经典的库伦摩擦模型分析了部分物理参数对系统的瞬态动力学和不稳定性的影响。由于库伦摩擦模型在相对速度接近零时的突变性，模型在数学分析上存在局限。对此， Pilipchuk等［23］基于此将动静盘面间的摩擦系数变换关系进行光滑处理建立了刹车装置的分析模型。在现代刹车盘新材料技术发展的大环境下，上述模型存在一定局限。本文将动态摩擦系数处理为和盘面材料特性以及运动状态关联的函数形式，可依据实际试验数据导入模型计算，为后续新材料技术的发展预留模型接口。

由于刹车装置结构的复杂性，构建的模型往往表现出较强非线性特征，通常可采用数值分析方法进行研究。其中，Kang等［24］、Liu等［25］通过模型的数值分析结果得出了系统发生尖叫现象的极限速度。但当需要对结构进行参数化设计时，数值积分方法相对较为耗时。对此，有学者将复杂刹车模型中的非线性动力学分析做了如下研究： Sinou等［26?28］提出了一种基于中心流形概念的非线性策略用以研究系统临界稳定点附近的非线性动力学行为；也通过在平衡点附近线性化的方式利用雅可比矩阵的特征值来分析系统稳定性。这一方式虽简化了计算，但带来了一定程度上系统误差。

本文将基于飞机刹车装置制动环境变化明显的特点，建模时考虑盘面材料摩擦特性及液压作动系统的影响，建立刹车装置盘组动力学分析模型。由于模型中加入了等效机轮速度状态量，能利用模型分析已知的特定滑跑速度下刹车装置颤振问题，并利用数值仿真分析方法探究机轮速度、系统阻尼、盘面摩擦特性等参数对于系统稳定性的影响。考虑到系统表现出的较强的非线性动力学特征，采用分岔理论对系统的非线性动力学行为和临界稳定区域进行研究，揭示刹车诱发振动原理，进而形成一整套完备的刹车振动分析方法，用于指导飞机刹车装置减振优化和结构参数化设计。

1 飞机刹车盘组非线性动力学模型建立

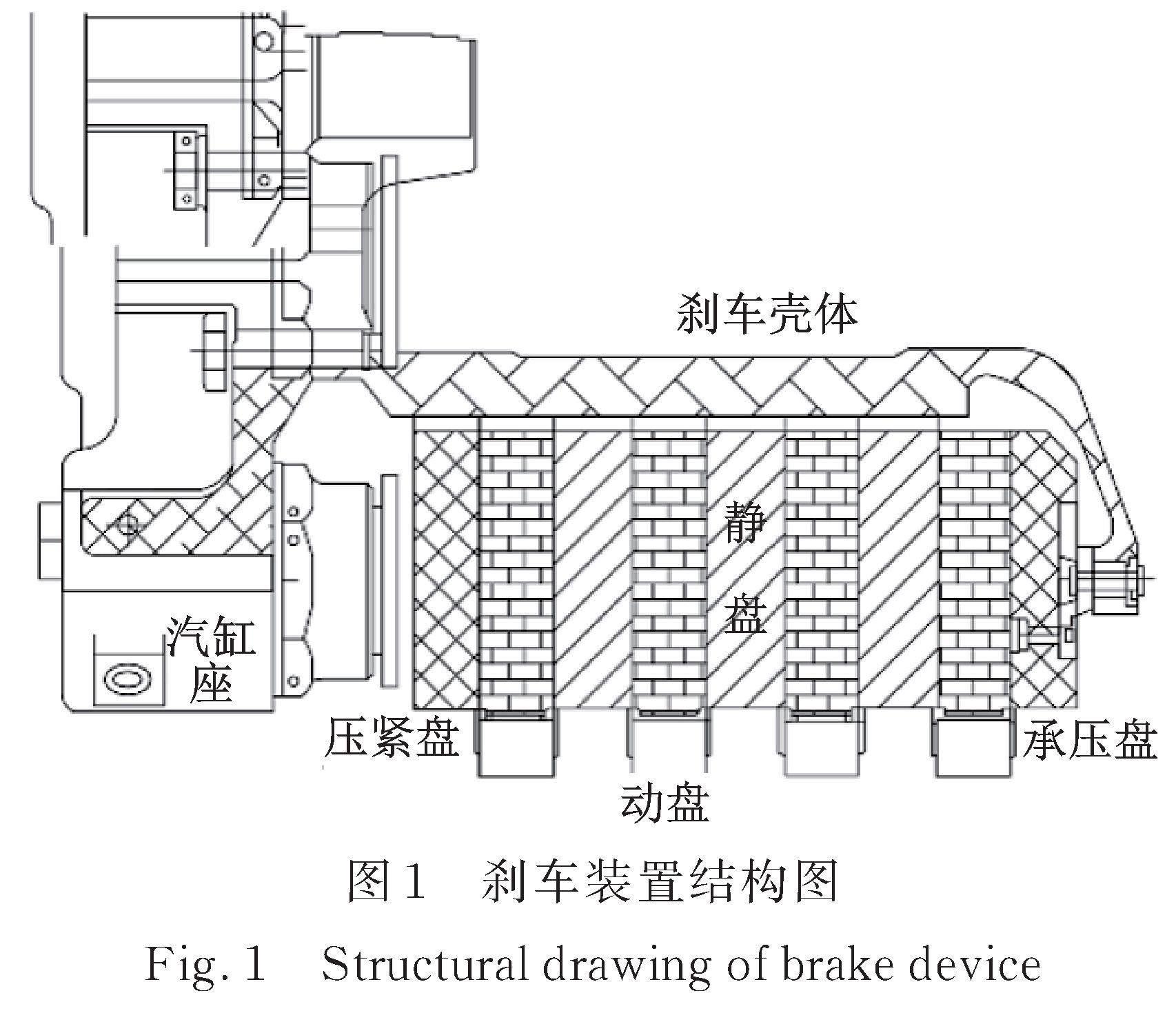
飞机刹车装置主体结构如图1所示。在刹车制动过程中，液压系统受防滑电流控制推动气缸座活塞沿轴向伸展，克服回力弹簧预紧力后将推动随机轮转动的动盘运动，进而动、静盘面挤压接触不断摩擦，产生刹车力矩对飞机进行减速制动。所以建立的数学模型应能准确描述上述实际的刹车过程。

通过对刹车装置结构作用原理的分析，将动、静盘组的相对运动等效为质量块和的三自由度运动。引入传送带模型用于模拟盘面间的摩擦制动效果，故传送带的速度可视为机轮等效速度，并对模型做出如下基本假设：

（1） 在转子旋转状态时，盘面摩擦力的方向不发生改变。

（2） 在施压过程中动静盘面一直保持接触和相对滑动状态，不发生脱离现象。

（3） 传送带速度为恒值，不受质量块运动影响。

在上述假设及分析下建立如图2所示的刹车盘组动力学分析模型，用于后续制动系统的稳定性分析。

模型中坐标系向定义为刹车盘轴向；向定义为刹车盘径向；，为刹车装置动盘径向等效刚度、阻尼；，为液压作动系统等效刚度、阻尼；，为动静盘面等效挤压刚度、阻尼，正常情况下当未加隔离垫时，默认为0。出于对由轮胎偏心运转或刹车压力作用不均而导致的盘面偏转情况考虑，在模型中将传送带垂直方向和施压方向所呈夹角设为，对系统进行动力学受力分析，表达式为：

式中为动盘、轮毂结构等效质量；为静盘等效质量；N为质量块m1与摩擦面之间的接触压力；f为液面活塞产生的刹车压力；盘面摩擦力T可表示为：

（2）

利用质量块的两个运动方向自由度的耦合关系式：

可将状态方程式（1）进行降阶处理，方便后续分析计算。

另外考虑在实际制动过程中，动、静盘面摩擦系数受盘面相对滑动速度等因素影响而非固定保持不变，也正是因为摩擦系数变化规律的复杂性致使产生不稳定的刹车力矩，一定程度上加剧振动，所以本文参考文献［29］将摩擦系数与盘面相对滑动速度v关联，具体表达式为：

（4）

式中，，，为多项式系数；滑动速度表示为：

（5）

将式（5）代入式（4）有：

取多项式系数向量为：

（7）

向量的取值在很大程度上决定了滑动速度对于摩擦系数的影响形式，可作为刹车盘面摩擦特性的数值表征值，为直观体现系统状态变量关系，将式（1）改写为如下所示的矩阵形式：

式中为状态向量；为质量矩阵；为阻尼矩阵；为刚度矩阵；为广义力矩阵。

式中为非线性项，为方便分析将其拆分为低阶非线性项和高阶非线性项：

（24）

低阶项在整个非线性项中较为关键，其具体表达式为：

从非线性项（25）可以看出，由于建模时考虑了摩擦特性，系统表现出较强的非线性，传统的线性分析及线性化处理方法对制动系统（8）的稳定性分析受限。鉴于此，后续采用数值仿真计算及非线性理论分析两种方法进行刹车诱导振动稳定性的相关研究工作。

2 数值仿真计算

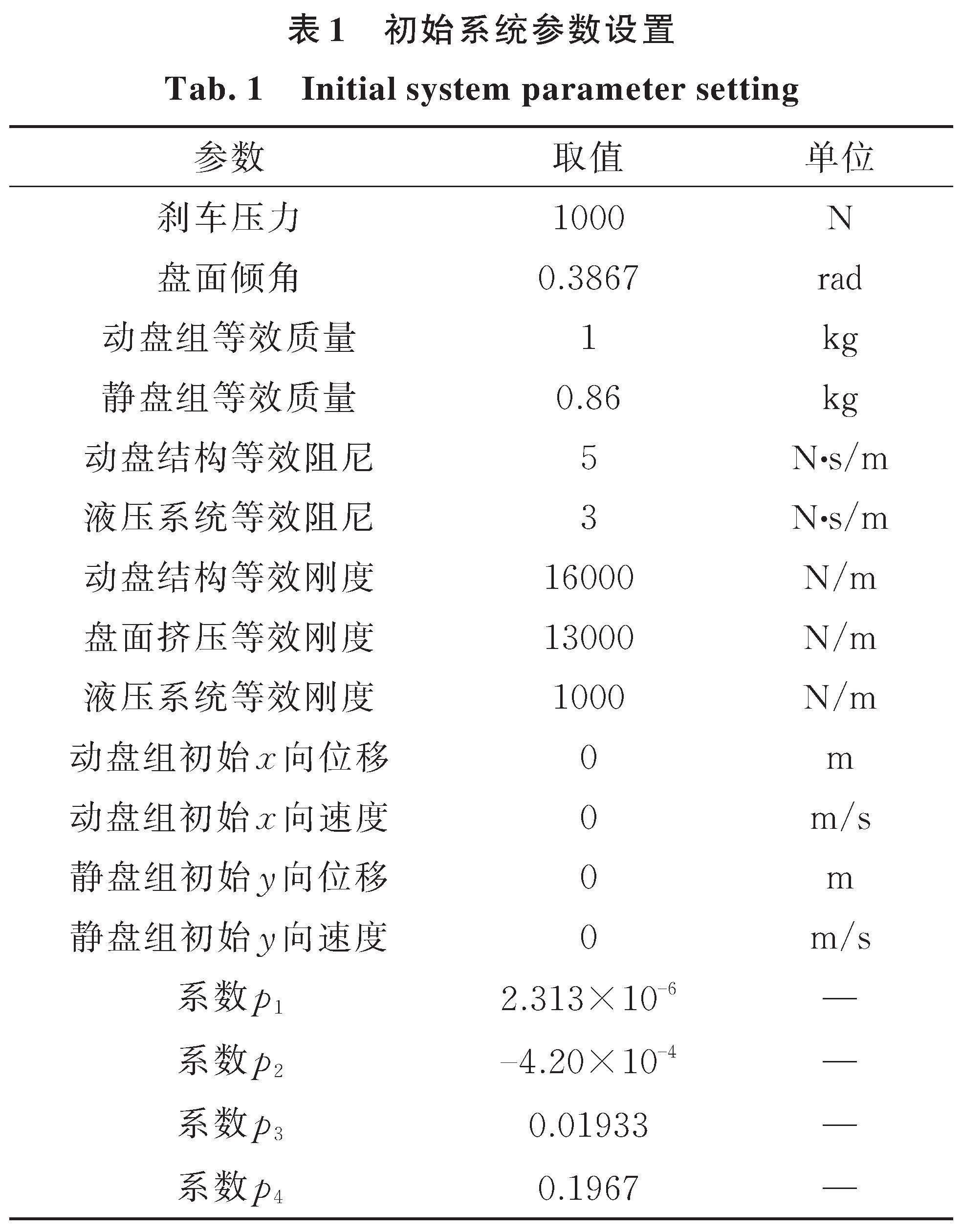
对于大多数的非线性系统往往都不能轻易找到解析解，可借助数值方法进行时域仿真分析。采用ode45算法进行系统振动位移响应仿真，初始条件设置参考文献［17］中的相关参数设定，如表1所示。

通过控制变量法来探究各个参数对质量块的振动趋势影响。由于模型中所涉及到的系统参数和动静盘结构特性相关参数等在实际中可允许波动范围不大，相对而言机轮速度这类参数在制动过程中拥有较大的变化幅度，所以为了针对性地分析结构和系统参数对于制动稳定性的影响，并为刹车装置实际减振设计提供指导，本节中将选择系统阻尼和外部环境（等效机轮速度）作为主要控制变量进行仿真分析。

2.1 机轮速度影响分析

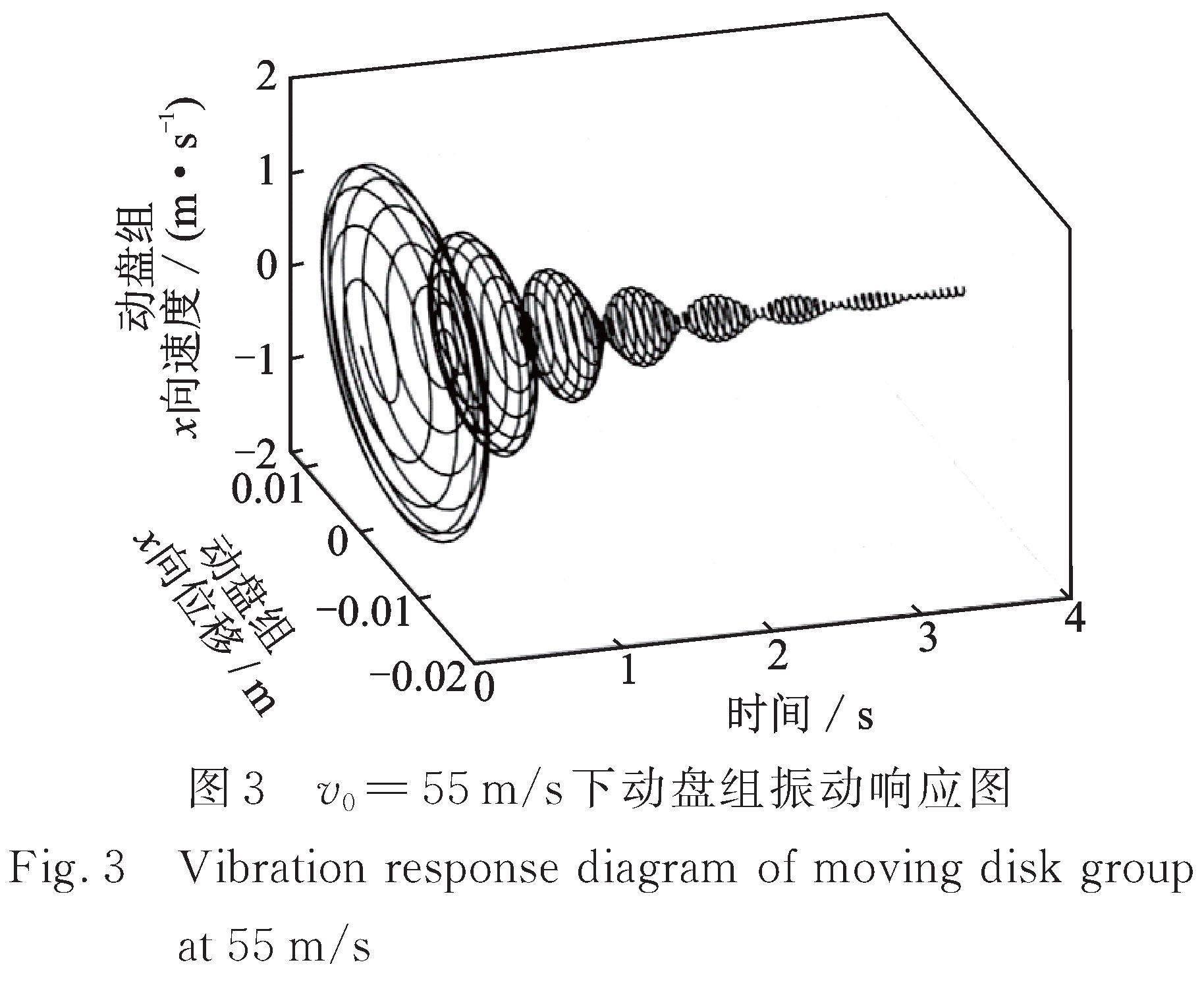
飞机刹车盘的制动颤振现象往往在一定滑跑阶段下发生。分别对应高、中、低速滑跑阶段取三种工况（55，35，15 m/s）进行数值仿真计算，固定其余参数，得到的质量块振动响应如图3～5所示。

由图3～5可知，随着等效机轮速度不断增大，质量块位移响应经历了从收敛到等幅振荡再到周期降幅收敛的振动形式转换。初始15 m/s机轮速度情况下，质量块位移振幅经短暂增加极大值后急剧下降并收敛于稳态值A附近，机轮速度增加到35 m/s时，振动幅度增加到后保持稳定，这种等幅振荡运动现象一般出现于非线性系统的强迫振荡中。考虑刹车装置机械结构约束，实际振动幅值的确定将依据以下原则：当系统等幅振动幅值小于机械结构约束时，振动幅值为；当系统等幅振动幅值大于机械结构约束时，振动幅值为结构限制约束位移；当增大至55 m/s时，振动位移响应趋于收敛，但与15 m/s下系统收敛态势存在明显差异，收敛速度减缓且不断来回振荡。由上述分析，机轮速度将影响到系统稳定性，且在滑跑中期刹车振动发生的可能性较大。

2.2 系统阻尼影响分析

所建立的刹车盘组动力学分析模型中系统阻尼主要包含液压系统等效阻尼、刹车盘面阻尼两部分，其中液压系统等效阻尼用于对液压油路中节流阀等阻尼结构对刹车压力的变化速率影响进行模拟。刹车盘面等效阻尼由减振措施中隔离垫的加入所产生。

2.2.1 液压系统等效阻尼影响分析

固定其余参数，令，取不同液压系统等效阻尼进行数值仿真分析，得到质量块的振动位移响应如图6所示。

由图6可知，在系统稳定区域内随液压系统等效阻尼的增大，系统振动幅度有明显减缓趋势。局部放大图数据显示，在基准液压系统等效阻尼基础上分别增减时，最大振动位移处的幅值对应变化量为左右。

2.2.2 刹车盘面等效阻尼影响分析

固定其余参数，令，分别取不同刹车盘面等效阻尼进行数值仿真计算，得到质量块的振动位移响应如图7所示。

由图7可知，在基准刹车盘面等效阻尼基础上分别增减时，最大振动位移处的幅值对应变化量为左右。所以无论是液压系统等效阻尼还是刹车盘面阻尼，随着阻尼参数的增大，质量块的振动位移、速度都将有一定衰减趋势。

3 非线性动力学行为及稳定性分析

在数值仿真计算方法中，通过时域仿真得到了特定参数下的系统响应，依据仿真结果可大致判断机轮速度等参数对系统振动响应的影响趋势，但这一方法在临界稳定区域确立、系统分岔特性研究方面存在局限，借助分岔理论等非线性分析方法，对系统进行稳定性分析。

3.1 系统Hopf分岔点

在机轮速度影响分析中，质量块振动响应出现了等幅振荡的运动形式，实际上在Hopf分岔点附近有可能出现这一情况，对于非线性系统，其具体定义如下：

若对给定的和，如果存在定义于邻域中的充分光滑函数和，且满足如下的 Hopf 分岔条件：

是的特征值；

；

；

则（，，）为系统的一个 Hopf 分岔点。

计算得到不同液压系统等效阻尼参数下系统Hopf分岔点如表2，3所示。

对于每一个固定的液压阻尼参数值，系统会搜寻到两个Hopf分岔点，其中较小机轮速度值对应的分岔点为表2中～，较大机轮速度值对应的分岔点为表3中～。通过改变系统参数能改变临界Hopf分岔参数值进而影响系统稳定性，为研究在Hopf分岔点附近系统的动力学行为，将系统参数设置为分岔点对应值，得到两质量块的相图如图8，9所示。

由相图可知，在Hopf分岔点附近系统的相图均聚焦到某一极限环上，相比于质量块和质量块的相图由外向内收敛，且极限环中心点的位移量不再为0，这主要是恒定刹车力的外部激励的作用结果。在Hopf分岔点附近，系统处于临界稳定状态，对应的振动形式表现为等幅周期振荡，利用这一性质来确定系统参数稳定区域，为刹车装置参数化设计提供帮助。

3.2 系统稳定性分析

利用系统在Hopf分岔点处表现出来的动力学行为特性，确定非线性系统稳定区域如图10所示。

对比影响因素时域分析，在固定液压系统等效阻尼情况下，增大机轮速度系统将经历稳定到不稳定再到稳定的状态变换；同样情况固定机轮参数情况下，增大液压系统等效阻尼可增强系统稳定性，这和数值仿真计算结果保持一致，验证了稳定性分析的有效性，进而借助其分析刹车盘面摩擦特性对系统稳定性的影响。

通过改变式（7）中的参数向量来实现对不同刹车盘面材料的模拟，参考文献［21］中A320国内零部件制造PMA件及国外样件OEM件碳基材料，取两组参数向量值如下：，

，对应的刹车盘面摩擦系数与滑动速度之间的关系如图11所示。

图11中，对应的刹车盘面材料摩擦系数变化范围宽、峰值为0.47，相比之下，对应的刹车盘面摩擦系数变化幅度较小，但所能提供的最大摩擦系数为0.42左右。固定其余参数（，）得到系统临界稳定图如图12所示。

由图12可知，两组摩擦特性参数临界稳定曲线将参数空间切割成了三大区域，对应区域内系统的稳定状态如表3所示。其中区域Ⅱ为摩擦特性参数向量由变化为后系统扩充的稳定区域，对比两组参数值可以得出结论：在机轮速度一定情况下，摩擦系数较大的刹车盘面材料达到系统稳定所需要的液压系统阻尼更大，系统不稳定参数范围更广。

4 振动减缓措施研究

通过前面的分析知道了刹车诱导振动的几类影响因素和具体的影响形式，考虑从以下几个方面采取减振措施减缓刹车振动。

4.1 增大系统阻尼

由2.2节系统阻尼影响分析，将系统阻尼，增大30%时，对应最大振动位移幅值能降低10%和4%左右，所以可基于上述分析采取减振措施，对应实际刹车装置，实施增大系统阻尼参数的方法如下：

（1） 在液压油路中安装节流器，安装节流器能有效抑制刹车压力的变化速率，实现增大液压系统等效阻尼的效果。

（2） 在刹车盘面间增添隔离垫形成阻尼层，如图13所示在传统制动盘单片一体式结构设计基础上，将静盘切分为两部分，并在两者间填充减振垫结构，一方面能使动静盘面受力更为均匀，另一方面也能等效增大系统刹车盘面阻尼，减缓刹车装置振动幅度，吸收系统振动能量。

事实上，波音747的动盘二合一技术和757的静盘减振垫结构设计也体现了上述方法的合理性［9］，另外相较于传统刹车盘组件的动、静盘密实结构，其无缓冲压缩，在加载刹车压力时刹车力矩被迅速建立，从而在短时间内产生力矩冲峰，造成对起落架结构产生较大冲击振动，降低飞机安全和舒适性能，所以加入隔离垫后的刹车装置不仅能减缓制动过程中的刹车盘面颤振，还能对起落架结构抖振起到一定缓解作用。

4.2 改善刹车盘面材料加工制造工艺

由3.2节分析可知，对于不同的刹车盘面材料，系统稳定性存在差异， 所以可以通过改善盘面材料或加工制造工艺的方式来减缓振动。盘面摩擦特性总体优化方向为：适当降低刹车盘面摩擦系数峰值；提升盘面摩擦系数不受环境干扰性。通过降低刹车盘面摩擦系数峰值，能够有效增大系统稳定参数范围，减缓抖振现象的发生，但同时需要提升摩擦系数抗干扰性以补充损失的刹车效率。以前文中A320的刹车盘为基础，依据优化方向生成的理想盘面材料摩擦性能如图14所示。

为评价制动盘的刹车效率，定义参数为：

式中为常规制动速度上限。将上述刹车盘面材料进行系统稳定性分析，得到结果如表5所示。

相比于PMA件，OEM件对应的不稳定轮速区间跨度只有12.87，具备更优的减振表现，但却损失了较多的刹车效率，而优化后的理想件不仅不存在发散区间，而且由于其摩擦系数抗干扰性获得了最高的刹车效率，所以理想件的材料属性是未来制动器优化的方向。

4.3 优化防滑刹车控制策略

由机轮速度影响和稳定性分析可知，当速度处于临界Hopf分岔值范围内时，系统振动形式趋于发散，易引发结构性破坏，对此考虑建立如图15所示含减振通道的飞机防滑刹车控制系统。

减振通道设计策略为：由系统稳定性分析在参数空间内确定实际刹车装置结构参数对应的极限速度与，将实时机轮速度与极限速度的差值作为控制器的输入，在危险速度范围内适当减小刹车压力，并在稳定速度范围内适当增大刹车压力，通过这样提升刹车效率的方式，实现保障刹车过程整体制动效率的同时，减缓刹车振动的效果。

式中为传统PBM式防滑刹车系统控制电流；为刹车效率补充电流；为减振通道作用电流；为机轮速度。

为验证上述减振设计策略的有效性，将所建立的刹车盘组模型加入到图16所示的飞机地面制动滑跑动力学模型中进行仿真分析。

图17和18为加入减振设计策略前后刹车装置动盘的振动响应。从振动位移和加速度可以得出，制动中期受机轮速度影响，传统防滑控制策略下的刹车装置振动幅度存在明显跃升现象，而优化后的控制策略能在危险范围内通过及时调整刹车压力的方式有效减缓了振动，从而验证了这一方法的有效性。

5 结  论

为了研究飞机刹车诱导振动的产生机理和参数影响形式，基于关键的刹车盘面摩擦特性、飞机滑跑速度、刹车装置结构参数三类致振因素，利用所建立的刹车盘组非线性动力学模型进行仿真和稳定性分析，主要结论可归纳为以下几点：

（1） 机轮速度和系统阻尼的不合理取值能诱发刹车振动，其中在结构参数固定情况下，机轮速度存在上下极限值，在滑跑中期系统振动幅度加剧，增大系统阻尼能有效减缓振动。

（2） 由于盘面摩擦系数等非线性因素的作用，系统存在极限环等非线性动力学行为，通过分岔理论等非线性分析方法得到：摩擦系数峰值高、刹车盘面摩擦特性不稳定的材料更易引发结构振动，并一次性确定了系统的临界稳定参数曲线，为结构设计提供了重要的分析手段。

（3） 基于稳定性分析结果，提出了几种刹车装置减振优化措施，具体措施为：①通过填充减振垫或安装节流器的方式适当增大系统阻尼；②改善刹车盘加工制造工艺，适当降低峰值摩擦系数，提升盘面摩擦系数的抗干扰性；③优化防滑刹车控制策略，在维持刹车效率的条件下，在制动中期引入减振通道设计，有效抑制振动响应幅度。

上述结论为研究人员提供了刹车装置减振优化方向，并通过仿真分析验证了优化措施的可行性，研究人员可基于本文所提出的模型和非线性分析方法，结合实际情况调整参数，进行相关理论研究。

参考文献：

［1］      Khapane P D .Gear walk instability studies using flexible multibody dynamics simulation methods in SIMPACK［J］. Aerospace Science & Technology， 2006， 10（1）：19-25.

［2］      Enright J J. Laboratory simulation of landing gear pitch-plane dynamics［J］. SAE Transactions，1985，94：857-866.

［3］      库玉鳌. 刹车与起落架抖动的相互影响［J］.航空学报，1996，18（2）：228-230.

Ku Yuao. Interaction between braking and landing gear vibration［J］. Acta Aeronautica et Astronautica Sinica， 1996，18（2）：228-230.

［4］      Khapane P D. Simulation of asymmetric landing and typical ground maneuvers for large transport aircraft［J］. Aerospace Science and Technology， 2003， 7（8）： 611-619

［5］      Khapane P D. Gear walk instability studies using flexible multibody dynamics simulation methods in SIMPACK［J］. Aerospace Science and Technology， 2006，10（1）：19-25.

［6］      尹乔之， 聂宏， 张明， 等. 某半轴支柱式起落架低频刹车诱导振动特性研究［J］.振动工程学报，2016，29（6）：954-962.

Yin Qiaozhi， Nie Hong， Zhang Ming， et al. Vibration characteristics of gear walk on half-axle landing gear［J］. Journal of Vibration Engineering， 2016，29（6）： 954-962.

［7］      张陵， 诸德培.主起落架纵向抖振的动态特性研究［J］.航空学报，1996，17（3）：292-296.

Zhang Ling， ZHU Depei. On the dynamic properties of landing gear walking［J］. Acta Aeronautica et Astronautica Sinica， 1996，17（3）：292-296.

［8］      杨尊社， 娄金涛， 张洁， 等. 国外飞机机轮刹车系统的发展［J］.航空精密制造技术，2016，52（4）：40-44.

Yang Zunshe， Lou Jintao， Zhang Jie， et al. Development of foreign aircraft wheel and brake system［J］. Aviation Precision Manufacturing Technology， 2016，52（4）：40-44.

［9］      常飞， 何永乐. 基于飞机刹车振动问题的研究［J］. 装备制造技术， 2013 （1）：119-121.

Chang Fei， He Yongle. Based on the aircraft brake vibration research［J］. Equipment Manufacturing Tech-nology，2013（1）：119-121.

［10］    王红玲， 田广来， 李国胜，等. 航空机轮刹车振动的仿真分析［J］. 航空精密制造技术， 2014 （1）：49-53.

Wang Hongling， Tian Guanglai， Li Guosheng， et al. Research and analysis vibration mechanism of aircraft wheel brake［J］. Aviation Precision Manufacturing Technology， 2014（1）： 49-53.

［11］    Li F Z， Tong S G. The vibration and modal analysis of the disc brake［J］. Advanced Materials Research， 2013， 774-776：78-81.

［12］    孟德建， 张立军， 阮丞， 等. 摩擦引起的制动器热点问题综述［J］.同济大学学报（自然科学版），2014，42（8）：1203-1210.

Meng Dejian， Zhang Lijun， Ruan Cheng， et al. Literature survey of friction-induced hot spots in brakes［J］. Journal of Tongji University （Natural Science）， 2014， 42（8）： 1203-1210.

［13］    孟德建， 张立军， 余卓平. 通风盘式制动器热?机耦合理论建模与分析［J］.同济大学学报（自然科学版），2010，38（6）：890-897.

Meng Dejian， Zhang Lijun， Yu Zhuoping. Theoretical modeling and FEA of thermo-mechanical coupling dynamics of ventilated disc brake［J］. Journal of Tongji University （Natural Science）， 2010， 38（6）：890-897.

［14］    Wu B W， Qiao Q F， Chen G X， et al. Effect of the unstable vibration of the disc brake system of high-speed trains on wheel polygonalization［J］. Proceedings of the Institution of Mechanical Engineers， Part F： Journal of Rail and Rapid Transit， 2020， 234（1）：80-95.

［15］    Wang Zhiwei， Zhang Weihua， Yin Zhonghui ， et al. Effect of vehicle vibration environment of high-speed train on dynamic performance of axle box bearing［J］. Vehicle System Dynamics， 2019，57（4）：543-563.

［16］    Hagler L B， Reinhall P G. Friction induced vibrations in aircraft disk brakes［C］∥ASME 1997 Design Engineering Technical Conferences. 1997：1-9.

［17］    Dupac M A，  Raju P K. Vibration analysis of a brake mechanism： modeling， simulation and experimental results［C］∥ASME International Design Engineering Technical Conferences & Computers & Information in Engineering Conference. 2005：925-931.

［18］    Leine R I， Campen D， Kraker A D， et al. Stick-slip vibrations induced by alternate friction models［J］. Nonlinear Dynamics， 1998， 16（1）：41-54.

［19］    贾尚帅，丁千.刹车系统的摩擦自激振动和控制［J］.工程力学，2012，29（3）：252-256.

Jia Shangshuai， Ding Qian. Friction-induced self-excited vibration and control of a brake system［J］. Engineering Mechanics， 2012，29（3）：252-256.

［20］    Meehan P A. Prediction and suppression of chaotic in-stability in brake squeal［J］. Nonlinear Dynamics， 2022， 107（1）：205-225.

［21］    Tan C A， Li J. A parametric study on the friction-induced vibration of a brake model during decelerated sliding［C］∥ASME International Design Engineering Technical Conferences & Computers & Information in Engineering Conference. 2005：933-939.

［22］    Meehan P A. Prediction of wheel squeal noise under mode coupling［J］. Journal of Sound and Vibration， 2019， 465（3）：115025.

［23］    Pilipchuk V N， Ibrahim R A， Blaschke P G. Disc brake ring-element modeling involving friction-induced vibration［J］. Journal of Vibration and Control， 2002， 8（8）：1085-1104.

［24］    Kang J， Krousgrill C M， Sadeghi F. Comprehensive stability analysis of disc brake vibrations including gyroscopic， negative friction slope and mode-coupling mechanisms［J］. Journal of Sound & Vibration， 2009， 324（1-2）：387-407.

［25］    Liu S Y， Gordon J T， Oezbek M A. Nonlinear model for aircraft brake squeal analysis： model description and solution methodology［J］. Journal of Aircraft， 1998， 35（4）：623-630.

［26］    Sinou J J， Dereure O， Mazet G B， et al. Friction-induced vibration for an aircraft brake system—Part 1： experimental approach and stability analysis［J］. International Journal of Mechanical Sciences， 2006， 48（5）：536-554.

［27］    Sinou J J， Thouverez F， Jezequel L， et al. Friction induced vibration for an aircraft brake system—Part 2： nonlinear dynamics［J］. International Journal of Mechanical Sciences， 2006， 48（5）：555-567.

［28］    Sinou J J， Thouverez F， Jezequel L. Analysis of friction and instability by the centre manifold theory for a non-linear sprag-slip model［J］. Journal of Sound and Vibration， 2003， 265（3）：527-559.

［29］    逯九利. 飞机制动控制系统综合性能研究［D］.西安： 西北工业大学，2020.

Lu Jiuli， Research on comprehensive performance of aircraft brake control system［D］. Xi′an： Northwestern Polytechnical University，2020.

Stability analysis and vibration reduction design of aircraft brake induced chatter

Abstract： Taking aircraft brakes as the research object， the problem of aircraft brake induced vibration was studied. Aiming at the influence of disc friction characteristics caused by the complex braking environment during aircraft skidding， a nonlinear dynamic analysis model of brake disc set was established considering the properties of the hydraulic system and disc material， with the model interface reserved for the development of new material technology. From the perspective of practical engineering research value， the influence of the above parameters on the stability of the system is studied by using numerical simulation， bifurcation theory， and other nonlinear analysis methods by considering key factors such as wheel speed， hydraulic system equivalent damping， brake disc surface damping and brake disc friction characteristics as control variables， and the range of structural parameters to keep the system stable is determined. It is convenient to parameterize the structure for rapid analysis and design. Based on the results of the model analysis， part of the causes of brake vibration were revealed， and corresponding optimization measures for vibration reduction were put forward from two aspects of structural parameters and brake control law. Then a comprehensive analysis method for aircraft brake induced flutter was formed， which provided a theoretical reference for the initial stage of aircraft brake design.

Key words： brake induced vibration；nonlinear model；bifurcation theory；stability analysis；vibration reduction measures