多级多重模态减缩策略及其在转子系统动力学特性分析上的应用

姚毅 黄行蓉 管晓乐 徐迅 张大义

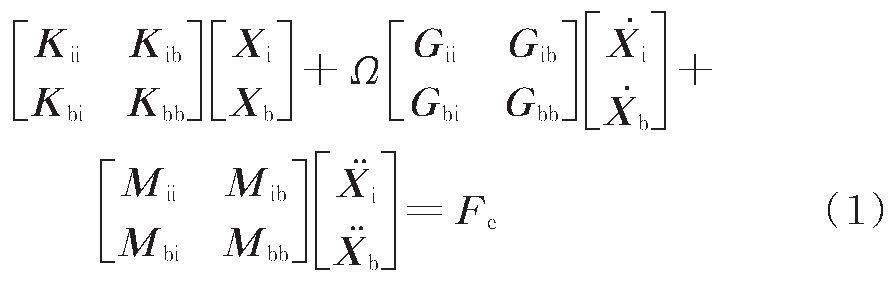
摘要： 航空发动机转子部件众多，多部件高维复杂系统计算量大，导致动力学分析困难、计算时间长，进而影响转子结构设计和动力学验证的效率。基于部件模态综合方法，提出一种针对多部件高维复杂系统降维计算的多级模态减缩策略。对每个单独的子结构利用固定界面模态减缩，并行减缩各子结构的内部自由度，同时完整保留子结构间的耦合关系。通过子结构组合定义新一级的子结构，应用多级模态减缩策略提升降维减缩效果，结合多重模态减缩方法，构建界面分支模态，可显著降低转子有限元模型的维数，同时保留关键子结构的动力学特征和系统整体关键动力学特性。此计算策略被用于某弹用发动机转子系统低维减缩模型的建立，利用减缩模型提升了转子动力学分析的效率，加速轴承刚度参数的优化设计。研究结果表明，与ANSYS计算相比，转子动力学分析所需时间降低了99.5%，精度误差不超过0.1%，该计算策略可用于多部件高维复杂系统的快速分析。

关键词： 转子动力学； 部件模态综合； 多级模态减缩； 模态减缩； 部件优化

中图分类号： O347.6    文献标志码： A    文章编号： 1004-4523（2024）05-0737-10

DOI：10.16385/j.cnki.issn.1004-4523.2024.05.002

引  言

准确预测转子系统的动力学特性，如临界转速等，对航空发动机等旋转机械的结构设计和动力学优化设计非常重要。有限元方法能够充分模拟多部件转子结构复杂的几何、材料等结构特征，较为精确地计算转子的动力学特性，在实际转子的动力学分析和优化设计中得到了广泛应用［1?3］。然而，有限元方法的精确计算通常要求大量的自由度，转子动力学特性预测需要在不同转速下多次计算转子结构的模态，需要大量的计算资源［4］。并且，在多部件转子系统结构优化设计中，对少数参数的调整（如轴承刚度参数）均需要重新计算转子系统的动力学特性，进一步加重了计算资源的负担，进而影响转子系统结构设计的效率。如何在保证计算精度的前提下，实现多部件高维复杂模型的动力学特性快速分析成为转子系统动力学优化设计中不可回避的问题。

部件模态综合方法是高维复杂模型常用的降维计算方法之一。左彦飞等［5?6］、马威猛等［7］采用部件模态综合方法减缩三维有限元转子模型，能够减少转子模型87%的自由度数目，节省80%左右的计算资源。孙传宗等［8］将固定界面模态减缩方法应用于单转子和双转子系统的降维，通过对比临界转速和固有振动特性验证了缩减模型的准确性。寇海江等［9］建立了盘片轴一体化结构的低维减缩模型，给出了一种模态保留阶数的选取原则。

对于多部件复杂结构，以传统方式应用模态综合方法建立的减缩模型自由度数量仍然很高，并且在模态综合方法的应用过程中，模型矩阵的稀疏性会被破坏，甚至出现“自由度数量减少，计算量反而增加”的情况［10］。

多重模态减缩方法和多级模态减缩方法基于传统模态综合方法，进行多次减缩计算，进一步减少自由度数量，提升减缩效果。高峰等［11］应用双重减缩建模方法建立了失谐叶盘的减缩低维模型，与实验结果对比验证了其准确性。黄行蓉等［12?13］、Yao等［14］结合对称化方法提出适用于声固耦合系统的多重模态减缩方法，并提出了一种选取模态保留数量的策略。Huang等［15］将多重模态减缩方法应用于控制优化，以提升数值计算的效率。Jin等［16］在第一重模态减缩后进行模态拓展，提升双重模态减缩方法的精度，并将其应用于双盘转子的减缩计算。Wang等［17］通过对比分析，发现双重模态减缩和三重模态减缩两种减缩方式的精度差别受子结构划分方式的影响。和非线性模态理论结合，多重模态减缩方法越来越广泛地被应用于非线性系统动力学特性的分析［18?19］。

多重模态减缩方法是根据子结构间耦合关系，依次对各子结构进行减缩降维，只能串行计算；而多级模态减缩方法在子结构划分阶段即区分了子结构间的从属关系，同一级子结构的减缩可以同时进行，下级子结构减缩模型作为上级子结构的一部分参与上级子结构的减缩计算。Elssel等［20］采用“二叉树”的形式分级划分子结构，每一级子结构分解为两个下级子结构自由度、交界处自由度和保留自由度，通过忽略下级子结构的高阶模态，逐级组合得到整体模型的减缩模型。在大型转子系统特征值求解中的应用证明了此多级模态减缩方法的有效性。但“二叉树”形的子结构划分方式不一定完全适应大型转子结构各部件间的复杂耦合关系。

本文针对多部件高维复杂模型计算量大的问题，基于部件模态综合方法，提出了一种多级模态减缩策略。首先，基于固定界面模态减缩方法，介绍了多级模态减缩策略的原理和流程。接着，利用弹簧单元等效模拟轴承，将其定义为关键子结构，通过某弹用发动机转子系统的减缩建模实例，详细说明了多级模态减缩策略，以及与多重模态减缩方法结合的应用过程。然后，借助该实例的减缩效果和修改关键子结构刚度参数后的动力学特性快速分析，证明了多级模态减缩策略的有效性和优势，为多部件高维复杂模型的快速分析、提升优化设计效率提供了参考。

1 多级模态减缩方法

1.1 固定界面模态减缩方法

固定界面模态减缩方法是高维复杂结构降维过程中较为常用的方法之一，也被称为Craig?Bampton方法［21］。将转子系统分解为内部子结构和界面子结构，转子系统的动力学方程可写为：

式中 K，G 和M 分别表示刚度矩阵、陀螺矩阵和质量矩阵；X 表示位移；下标b 和i 分别用来标记界面子结构和内部子结构；Ω 表示转子转速；Fe 为外部激励力。

式中 U 表示位移振幅；j 表示虚数单位；ω 表示自由振动频率；t 表示时间。

对内部子结构进行减缩，其位移变量Ui 可以看作由两部分组成：（1）当界面子结构被约束，作用在内部子结构上的外载荷产生的位移；（2）由界面子结构引起的静态位移。表示为：

Ui = Φi qi + ΨiUb （3）

式中 Φi 表示通过求解内部子结构的自由度振动方程保留前Nir 阶的模态得到的模态矩阵；qi 为对应的模态坐标；约束模态Ψi =-K -1ii Kib。

减缩变量关系可表示为：

式中 Ib 表示与Ub 维数对应的单位阵；Ti 为减缩矩阵。通过对内部子结构的减缩，整体系统的维数降低，减缩后的自由振动方程为：

式中  减缩内部子结构后的各矩阵分别为：

1.2 多级模态减缩策略

为了解决多部件高维复杂结构计算的困难，本文基于固定界面模态减缩方法提出多级模态减缩策略。依据自然边界，将多部件复杂结构划分为n个一级子结构，且在各一级子结构内部区分界面自由度和内部自由度。将界面（boundary）自由度定义为和其他子结构有直接耦合的部分；内部（interior）自由度和其他子结构没有直接耦合关系，通过界面自由度和其他子结构间接耦合。

包括n个一级子结构的整体系统的自由振动方程可写为：

式中 S = K + jωΩG - ω2 M；上标b 和i 表示界面自由度和内部自由度；下标1，2 和n 表示子结构编号。

为减缩第k 个子结构内部自由度，通过固定界面模态减缩方法构建减缩矩阵Tk，分为两部分：（1）求解第k 个子结构内部自由度的局部模态Φik，保留前N irk 阶；（2）求解约束模态Ψ ibk 。最终组合得到减缩矩阵为：

式中 I 表示单位矩阵，其维数为N irk 。

应用Tk 减缩k 号子结构的内部自由度，完成第一级模态减缩：

在结构减缩过程中，基于子结构内部自由度和界面自由度的定义，对于k 号和k'号的两个子结构，其耦合关系体现在子结构的界面自由度之间的耦合矩阵Sbbkk'，k ≠ k'中，该项在多级模态减缩的单独一级模态减缩过程中不受影响，被完整保留在减缩子结构中，此特点可以保证子结构连接界面的动力学特性。

完成一次内部自由度的减缩后，有可能出现“自由度减少，计算量反而增加”的现象。其原因为减缩前的大型多部件动力学模型中的各项矩阵均为稀疏矩阵，而在减缩计算中，模态矩阵Φik 和约束模态Ψ ibk均为稠密矩阵。经过减缩计算，包括刚度矩阵、质量矩阵和陀螺矩阵在内的各项矩阵均变稠密，导致计算量增加，数据存储和矩阵计算更加困难。如果矩阵维数并未下降到一定量级，如103 量级，计算量仍然显著，甚至会超过减缩前的计算模型。

为了解决该问题，本文提出多级模态减缩策略，提升模型降维的程度，进一步降低减缩模型的计算量。在完成第一级模态减缩后，将邻近的若干一级子结构组合得到m 个二级子结构。将k 号二级子结构包含的自由度Vk 重新区分界面自由度V bk 和内部自由度V ik，转子整体系统的自由振动方程可写为：

式中 组合若干一级子结构得到二级子结构的局部动力学系统SS = K + jωΩG - ω2 M；V 表示二级子结构的幅值。

对二级子结构的内部自由度进行固定界面模态减缩，即可进一步降低整体系统的自由度数量。

在完成上一级子结构减缩计算后，评估子结构数量和自由度数量，如二者均比较多，则根据子结构耦合关系组合下一级的子结构，再次减缩其内部自由度；如果子结构数量较少，而自由度数量较多，则可以应用多重模态减缩策略进一步减缩子结构自由度；如果自由度数量较少，则完成减缩计算，得到多部件高维复杂结构的减缩模型。

在结构优化设计中，通常有部分结构参数需要多次调整，每次参数调整都需要进行动力学分析，计算其动力学特性，如航空发动机中的轴承刚度等。对于存在需要进行优化设计部件的多部件大型复杂结构，可以将其定义为关键子结构，不参与模态减缩，从而被完整保留到减缩模型中，以便在减缩模型中直接替换关键子结构参数，避免重复进行减缩计算。

综上，考虑关键子结构的多级模态减缩流程如下：

步骤1：确定需要进行优化设计的部件，作为关键子结构。

步骤2：划分子结构，将关键部件划分为单独子结构。

步骤3：根据子结构耦合关系，区别界面自由度和内部自由度。

步骤4：对各子结构的内部自由度进行减缩。

步骤5：将子结构间耦合项中的零矩阵缩减至减缩模型对应维数，得到一级减缩模型。

步骤6：评估子结构数量和自由度数量：如二者均比较多，则根据子结构耦合关系组合下一级的子结构，返回步骤3；如果子结构数量较少，而自由度数量较多，则应用多重模态减缩策略进一步减缩子结构自由度；如果自由度数量较少，则完成减缩计算，得到多部件高维复杂结构的减缩模型。

2 减缩实例

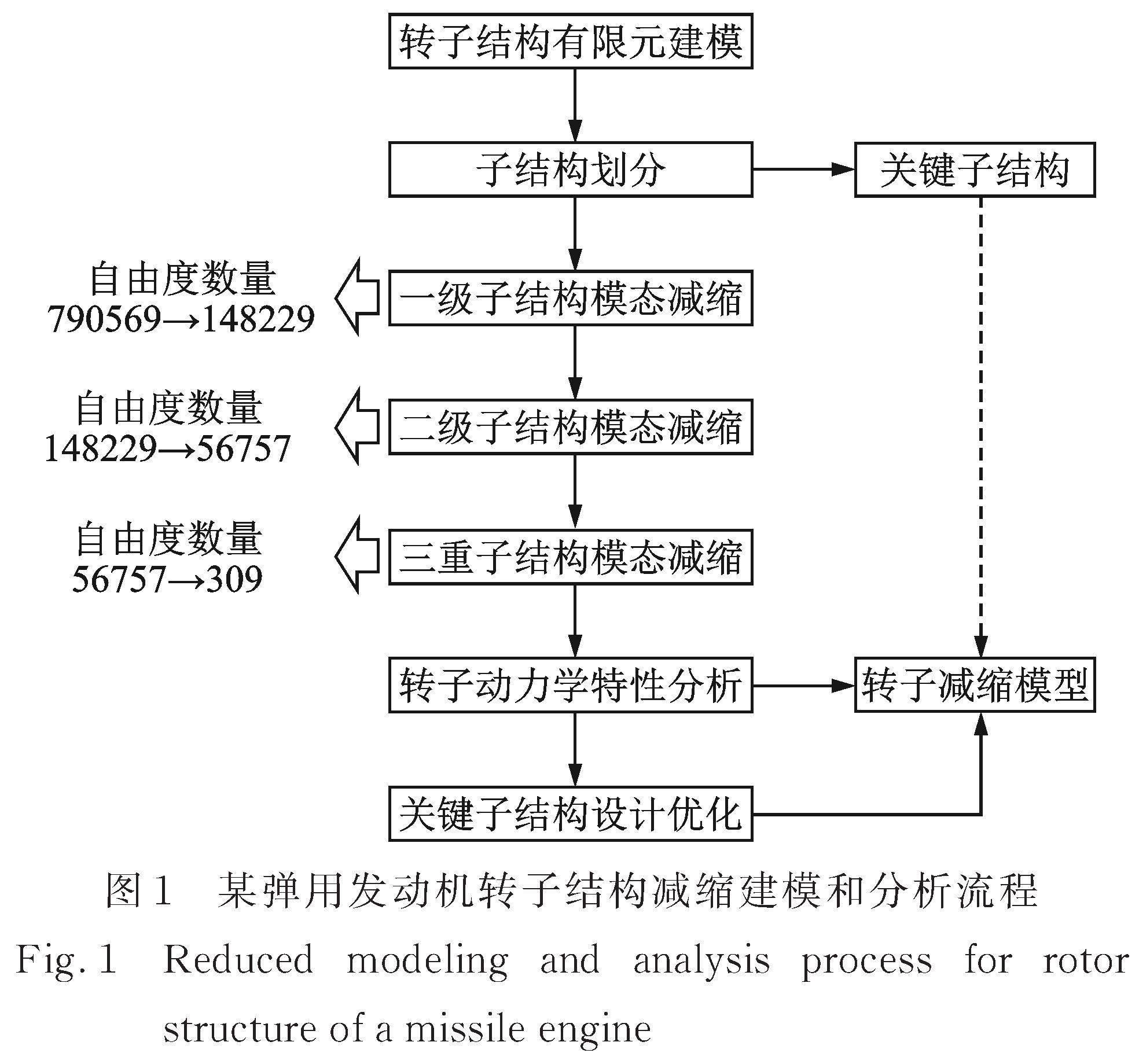
本节将多级模态减缩策略应用于某弹用发动机的简化转子模型动力学特性分析，以该实例具体介绍多级模态减缩策略的过程：建立发动机转子结构的有限元模型；转子模型被划分为18个一级子结构，定义关键子结构；首先减缩一级子结构的维数；在组合一级子结构得到二级子结构进行进一步降维的同时，缩减子结构数量；最后应用三重模态综合建立转子的减缩模型；基于减缩模型实现高效的转子动力学特性分析和关键子结构优化设计。流程图如图1所示。

2.1 一级子结构模态减缩

转子前后两个轴承处分别建有远程节点，通过建立弹簧单元等效轴承刚度［22］，将两个远程节点定义为1号子结构，其余一级子结构根据转子结构部件定义。转子整体结构共有18个一级子结构，各子结构的编号如图2所示。1号子结构定义为“关键子结构”，将关键子结构完全保留，不对其进行减缩。

转子转轴划分为2，3，4，12，13，16和17号子结构，轴流叶盘由5和6号子结构组成，7和8号子结构分别表示防振弹性环和轴?离转接座，离心叶盘由9，10，11和18号子结构组成，涡轮叶盘由14和15号子结构组成。转子各部件的自由度数量如表1所示，共有790569个自由度。

子结构内区分界面自由度和内部自由度，k号一级子结构的局部自由振动方程可写为：

以2 号一级子结构为例，2 号子结构仅与3 号子结构直接耦合，2 号子结构和3 号子结构的局部刚度矩阵的非零元素分布图如图3 所示。子结构之间的耦合关系体现为计算矩阵的非零元素，矩阵的计算量和非零元素的数量呈正相关，矩阵中非零元素的数量标注为图3 中的nz。红色框内为2 号子结构刚度矩阵，以黑色线分割为四部分，分别为K bb22，K ib22，K bi22和K ii22。其界面自由度和3 号子结构的界面自由度直接耦合，体现为非零矩阵K bb

23 和K bb

32；其余自由度之间

无直接耦合，耦合矩阵对应部分均为0 矩阵。

应用固定界面模态综合减缩k号一级子结构的内部自由度分4个步骤进行。

首先，求解内部自由度的局部自由振动方程：

K iikkU ik - ω2 M iikkU ik = 0 （11）

通过式（11）计算k 号一级子结构模态Φki，Φki满足：

式中 Λki 表示k 号一级子结构内部自由度被保留的前100 阶子结构模态对应的频率组成的对角矩阵；Iki 表示单位阵。

其次，根据k 号一级子结构内部自由度和边界自由度的耦合关系，求解约束模态Ψ ibkk：

Ψ ibkk =-K ii-1kk K ibkk （13）

再次，组合约束模态和k 号一级子结构内部自由度子结构模态得到k 号一级子结构的减缩矩阵Tk：

最后，对k号一级子结构刚度矩阵、质量矩阵和陀螺矩阵的减缩如下：

在一级子结构内部自由度减缩完成后，将各一级子结构之间的0耦合项缩减到对应维数。以2号一级子结构为例，一级子结构减缩后的2号子结构和3号子结构的局部刚度矩阵不再稀疏，如图4所示，稠密矩阵中的非零元素数量为43965194，远远大于图3所示稀疏矩阵中的3443638，维数降低，计算量反而增加。

经过一级子结构模态减缩，各子结构的自由度数量如表2所示，转子整体模型的维数从790569降低至148229。

2.2 二级子结构模态减缩

一级子结构模态减缩完成后，转子整体模型维数仍然较高，需要进行第二级子结构模态减缩。转子整体结构共有18个一级子结构，组合一级子结构得到的二级子结构如图5所示，图中斜体数字表示二级子结构的编号。1号子结构保持不变，1号子结构和其他子结构的耦合表征轴承刚度信息作为关键子结构保留；转轴段子结构合并为2号二级子结构，包括2，3，4，12，13，14，16和17号一级子结构；5，6，7和8号一级子结构组成3号二级子结构；9，10，11，15和18号一级子结构组成4号二级子结构。

将各二级子结构分别划分内部自由度和界面自由度，再次应用固定界面模态综合减缩各二级子结构的内部自由度。经过二级子结构模态减缩，转子各子结构自由度数量对比如表3所示，整体模型的维数从148229降低至56757。

2.3 三重模态减缩

经过两级子结构模态减缩，转子整体模型自由度数量从790569降低至56757，轴承刚度作为关键结构参数得以保留。模型的子结构数量较少，自由度数量仍然较多。在多级模态减缩的基础上，结合三重模态减缩方法，进一步降维。

2.3.1 4号子结构模态减缩

经过两级子结构模态减缩，转子整体模型共有4个二级子结构、56757个自由度。转子整体模型的自由振动方程可写为：

其中，关键子结构——轴承等效弹簧的刚度参数被保留在子结构刚度矩阵K11 中。

4号子结构和2号，3号子结构之间存在直接耦合关系，其子结构位移可看作由三部分构成：一是由2号子结构引起4号子结构的位移；二是由3号子结构引起4号子结构的位移；三是其他子结构被约束时，作用在4号子结构上的外力引起的位移。表示为：

U4 = Ψ42U2 + Ψ43U3 + Φ4 q4 （17）

式中 约束模态Ψ42 =-K -144 K42，Ψ43 =-K -144 K43；q4 为4 号子结构前100 阶模态幅值变量；4 号子结构前100 阶子结构模态Φ4 通过求解如下局部自由振动方程计算：

K44U4 - ω2 M44U4 = 0 （18）

且满足：

4号子结构的减缩矩阵构建为：

对4号子结构变量、刚度矩阵、质量矩阵和陀螺矩阵的减缩表示为：

转子整体模型的自由度数量从56757降低至40125。

对4号子结构的减缩中，作用在4号子结构上的外力引起的位移部分的高阶模态组分被忽略；由2号和3号子结构运动引起4号子结构的位移分别被凝缩在2号和3号子结构上。

2.3.2 3号子结构模态减缩

考虑静力学耦合效果，经过对4号子结构的减缩后，3号子结构和2号子结构之间存在直接耦合关系，其子结构位移可看作由两部分构成：一是由2号子结构引起3号子结构的位移；二是其他子结构被约束时，作用在3号子结构上的外力引起的位移。

由于在第一重模态减缩时，由3号子结构引起4号子结构的振动被凝缩在3号子结构的动力学系统中，此时求解的3号子结构的子结构模态为界面分支模态，包含了4号子结构对3号子结构的影响：

U3 = Ψ32U2 + Φ3 q3 （22）

式中 约束模态Ψ32 =-K r4-133 K r432；q3 为3 号子结构前100 阶模态幅值变量；3 号子结构前100 阶子结构模态Φ3 通过求解如下局部自由振动方程计算：

K r433U3 - ω2 M r433 U3 = 0 （23）

且满足：

3号子结构的减缩矩阵构建为：

对3号子结构变量、刚度矩阵、质量矩阵和陀螺矩阵的减缩表示为：

转子整体模型的自由度数量从40125降低至26085。

2.3.3 2号子结构模态减缩

只考虑静力学耦合，经过对4号和3号子结构的减缩后，2号子结构和1号子结构之间存在直接耦合关系，其子结构位移可看作由两部分构成：一是由1号子结构引起2号子结构的位移；二是其他子结构被约束时，作用在2号子结构上的外力引起的位移，表示为：

U2 = Ψ21U1 + Φ2 q2 （27）

式中 约束模态Ψ21 =-K r3-122 K r321；q2 为2 号子结构前100 阶模态幅值变量；2 号子结构前100 阶子结构界面分支模态Φ2 通过求解如下局部自由振动方程计算：

K r322U2 - ω2 M r322 U2 = 0 （28）

且满足：

2号子结构的减缩矩阵构建为：

对2号子结构变量、刚度矩阵、质量矩阵和陀螺矩阵的减缩表示为：

转子整体模型的自由度数量从26085降低至309。

三重模态减缩依次对4，3和2号二级减缩子结构进行模态减缩，转子整体模型的自由度数量从56757降低至309，得到最终的低维减缩模型。

关键子结构的刚度矩阵K11 被保留，通过修改1号子结构的刚度矩阵来调整前后轴承的刚度，利用减缩模型核算转子动力学特性，快速反馈优化设计结果。但需要注意的是，在修改替换矩阵元素时，需要考虑减缩附加项-K12 K r3-1

22 K21。

3 多级和多重模态减缩效果及其在关键部件优化设计上的应用

3.1 减缩策略效果

前后轴承的刚度分别设置为1×107和1×108 N/m，Y，Z两个方向刚度相同，忽略刚体模态，计算第2～5阶模态，得到坎贝尔图如图6所示。第一阶正进动临界转速为17443 r/min，第二阶正进动临界转速为44580 r/min。

采用ANSYS计算结果作为参考标准，各阶模态频率计算中，转速50000 r/min时第二阶反进动模态频率误差最大，ANSYS计算结果为595.38 Hz，减缩模型计算结果为595.76 Hz，最大相对误差为0.064%。

零转速下，根据ANSYS计算所得振型和减缩模型所得振型，计算修正模态置信因子［23］（ModMAC， Modified Modal Assurance Criterion），结果如图7所示。

ANSYS振型和ANSYS振型计算得到的MAC图如图7（a）所示，同阶模态振型计算得到的MAC值均为1，相邻对称模态振型计算得到的MAC值分布于0～1之间，其他模态计算得到的MAC值为0。第二阶和第三阶模态振型如图8所示。减缩模型振型和ANSYS振型计算得到的MAC图如图7（b）所示，其中由于振型减缩误差，减缩模型第二阶模态的MAC值稍小，其他振型的计算误差均在误差许可范围内。

ANSYS计算所用时间是3091 s，减缩模型计算用时12 s，计算效率提升了99.6%。

3.2 关键子结构优化设计

该转子工作转速范围为23750～47500 r/min，转子动力学分析得到第二阶正进动临界转速为44580 r/min。通过优化轴承设计调整轴承刚度，避免转子的正进动临界转速位于工作转速范围内。

当修改轴承参数时，减缩前自由振动方程式（6）中只有关键子结构1 号子结构的刚度矩阵K11 被修改，即减缩模型式（31） 中，仅K11 - K12 K r3-122 K21 中的K11 被修改，只要替换此刚度矩阵中的局部少量元素即可，该部分元素在减缩模型刚度矩阵的对应位置如图9 所示。无需计算减缩前的高维模型或重新建立减缩模型，可以节省大量的计算时间。

将前轴承Y方向、Z方向和后轴承Y方向、Z方向的刚度分别修改为1.07×107 ，3.63×106 ，9.82×106和3.94×106 N/m，计算得到坎贝尔图如图10所示。转子的一阶正进动临界转速为23295 r/min，小于23750 r/min，不在转子工作范围之内，可以确认转子工作安全。

采用ANSYS计算结果作为参考标准，前四阶模态频率计算中，转速50000 r/min时第三阶反进动模态频率误差最大，ANSYS计算结果为241.52 Hz，减缩模型计算结果为241.63 Hz，相对误差为0.046%。

4 结  论

本文针对多部件大型转子系统数值计算困难的问题，基于固定界面模态减缩方法，提出多级模态减缩策略，并应用于某弹用发动机转子结构的减缩计算和轴承刚度的优化设计，得到主要结论如下：

（1）解释了减缩过程中“自由度减少，计算量增加”数值现象的原因，所提出的多级模态减缩策略可以有效解决这一问题。

（2）多级模态减缩策略可以有效提升计算效率，并保证计算精度。在某弹用发动机转子结构的应用中，与多重模态减缩方法结合，模型维数从790569降低至309，2～5阶模态的最大误差不超过0.1%，计算效率提升了99.5%以上。

（3）当修改关键部件的参数时，多级模态减缩策略可以保留关键子结构，利用建立的低维减缩模型，可以快速进行数值验证，大大提升了关键部件优化设计的效率。

参考文献：

［1］      张大义，刘烨辉，梁智超，等.航空发动机双转子系统临界转速求解方法［J］.推进技术，2015，36（2）：292?298.

Zhang Dayi， Liu Yehui， Liang Zhichao， et al. Prediction for critical speed of double spools system in aero engines［J］. Journal of Propulsion Technology， 2015，36（2）：292?298.

［2］      章健，张大义，王永锋，等.共用支承?转子结构系统振动耦合特性分析［J］.北京航空航天大学学报，2019，45（9）：1902?1910.

Zhang Jian， Zhang Dayi， Wang Yongfeng， et al. Coupling vibration characteristics analysis of shared support?rotors system［J］. Journal of Beijing University of Aeronautics and Astronautics，2019，45（9）：1902?1910.

［3］      曾振坤，张大义，黄巍，等.径向支承刚度非对称转子系统振动特性分析［J］.推进技术，2022，43（2）：250?259.

Zeng Zhenkun， Zhang Dayi， Huang Wei， et al. Analysis of vibration characteristics of rotor system with asymmetric radial support stiffness［J］. Journal of Propulsion Technology，2022，43（2）：250?259.

［4］      张大义，刘烨辉，洪杰，等.航空发动机整机动力学模型建立与振动特性分析［J］.推进技术，2015，36（5）：768?773.

Zhang Dayi， Liu Yehui， Hong Jie， et al. Investigation on dynamical modeling and vibration characteristics for aero engine［J］. Journal of Propulsion Technology， 2015，36（5）：768?773.

［5］      左彦飞，王建军，马威猛.3?D有限元转子模型减缩的旋转子结构法［J］.航空动力学报，2014，29（4）：894?900.

Zuo Yanfei， Wang Jianjun， Ma Weimeng. Rotating substructure method for 3?D finite element rotor model reduction［J］. Journal of Aerospace Power， 2014， 29（4）： 894?900.

［6］      左彦飞，王建军.3?D有限元转子系统动力减缩的部件模态综合方法及应用［J］.航空动力学报，2016，31（8）：1929?1934.

Zuo Yanfei， Wang Jianjun. Component mode synthesis for dynamic reduction of 3?D finite element rotor system and its application［J］. Journal of Aerospace Power， 2016， 31（8）：1929?1934.

［7］      马威猛，王建军.非对称转子支承系统动力分析的约束模态减缩方法［J］.推进技术，2016，37（3）：534?539.

Ma Weimeng， Wang Jianjun. Restraint modal reduction method for dynamic analysis of asymmetric rotor bearing system［J］. Journal of Propulsion Technology， 2016， 37（3）：534?539.

［8］      孙传宗，陈予恕，侯磊.复杂结构双转子系统的建模及模型缩减［J］.航空动力学报，2017，32（7）：1747?1753.

Sun Chuanzong， Chen Yushu， Hou Lei. Modeling method and reduction of dual?rotor system with complicated structures［J］. Journal of Aerospace Power， 2017，32（7）：1747?1753.

［9］      寇海江，袁惠群，李岩，等.一体化转子系统动力分析的预应力模态综合法［J］.东北大学学报（自然科学版），2014，35（2）：263?267.

Kou Haijiang， Yuan Huiqun， Li Yan， et al. A prestressed component mode synthesis method for dynamics analysis of blisk?shaft integrated rotor［J］. Journal of Northeastern University （Natural Science）， 2014， 35（2）： 263?267.

［10］    Monjaraz Tec C D， Gross J， Krack M. A massless boundary component mode synthesis method for elastodynamic contact problems［J］. Computers & Structures， 2022， 260： 106698.

［11］    高峰，孙伟.涂敷硬涂层的失谐整体叶盘减缩建模及振动分析［J］.航空动力学报，2018，33（7）：1595?1605.

Gao Feng， Sun Wei. Reduced?order modeling and vibration analysis of mistuned blisk with damping hard coating［J］. Journal of Aerospace Power， 2018， 33（7）： 1595?1605.

［12］    黄行蓉，刘久周，李琳.基于非线性模态的复杂系统动力学特性分析方法［J］.北京航空航天大学学报，2019，45（7）：1337?1348.

Huang Xingrong， Liu Jiuzhou， Li Lin. Dynamic characteristics analysis method of complex systems based on nonlinear mode［J］. Journal of Beijing University of Aeronautics and Astronautics， 2019， 45（7）：1337?1348.

［13］    黄行蓉，姚毅，张大义.适用于优化建筑结构声振特性的多重模态减缩策略［J］. 振动工程学报，2023，36（4）：1015?1023.

Huang Xingrong， Yao Yi， Zhang Dayi. Hybrid mode synthesis strategy for optimizing vibro?acoustic characteristics of building structures［J］. Journal of Vibration Engineering，2023，36（4）：1015?1023.

［14］    Yao Y， Huang X R， Yang X D， et al. Symmetric formulations combined with component mode synthesis for analyzing coupled fluid?structure problems. Reviews and extensions［J］. Applied Mathematical Modelling， 2023， 115： 645?660.

［15］    Huang X R， Jézéquel L， Besset S， et al. Optimization of the dynamic behavior of vehicle structures by means of passive interface controls［J］. Journal of Vibration and Control， 2018， 24（3）： 466?491.

［16］    Jin Y L， Lu K， Huang C X， et al. Nonlinear dynamic analysis of a complex dual rotor?bearing system based on a novel model reduction method［J］. Applied Mathematical Modelling， 2019， 75： 553?571.

［17］    Wang B B， Liu J Z， Cao Z F， et al. A multiple and multi?level substructure method for the dynamics of complex structures［J］. Applied Sciences， 2021， 11（12）： 5570.

［18］    Huang X R， Jézéquel L， Besset S， et al. Nonlinear hybrid modal synthesis based on branch modes for dynamic analysis of assembled structure［J］. Mechanical Systems and Signal Processing， 2018， 99： 624?646.

［19］    Huang X R， Jézéquel L， Besset S， et al. Nonlinear modal synthesis for analyzing structures with a frictional interface using a generalized masing model［J］. Journal of Sound and Vibration， 2018， 434： 166?191.

［20］    Elssel K， Voss H. Reducing huge gyroscopic eigenproblems by automated multi?level substructuring［J］. Archive of Applied Mechanics， 2006， 76： 171?179.

［21］    Craig R R Jr， Bampton M C C. Coupling of substructures for dynamic analyses［J］. AIAA Journal， 1968， 6（7）： 1313?1319.

［22］    马艳红，何天元，张大义，等.支承刚度非线性转子系统的不平衡响应［J］.航空动力学报，2014，29（7）：1527?1534.

Ma Yanhong， He Tianyuan， Zhang Dayi， et al. Imbalance response of rotor system with nonlinear bearing stiffness［J］. Journal of Aerospace Power， 2014， 29（7）： 1527?1534.

［23］    Brehm M， Zabel V， Bucher C. An automatic mode pairing strategy using an enhanced modal assurance criterion based on modal strain energies［J］. Journal of Sound and Vibration， 2010， 329（25）： 5375?5392.

A multi?stage hybrid modal reduction strategy and its application to rotor dynamics analysis

Abstract： The large number of aero-engine rotor components and the large computational volume of high-dimensional complex models lead to difficult dynamic analysis and long computation times， which are disadvantageous to the efficiency of rotor structure design and dynamics verification. Based on the component modal synthesis method， a novel multi-stage modal reduction strategy is proposed for the modal reduction of a large complex system with many components. The internal freedom degrees of each sub-structure are reduced in parallel using fixed interface modal reduction， while the couplings between the substructures are retained completely. By defining a new level of substructure through substructure combination， the multi-stage modal reduction is applied to an additional reduction， and the hybrid mode synthesis is subsequently combined to construct the branch mode and significantly reduce the dimensionality of the rotor FEM model. Meanwhile， the dynamic characteristics of key substructures and the key dynamic characteristics of the vibration system are preserved. This computational strategy is used to establish a low-dimensional reduced model of a missile engine rotor system， and the reduced model is used to improve the efficiency of rotor dynamics analysis and accelerate the design optimization of bearing stiffness parameters. The results show that the time required for rotor dynamics analysis is reduced by 99.5%， and the accuracy error does not exceed 0.1% compared with ANSYS calculations. The computational strategy can be used for rapid analysis of multi-component high-dimensional complex systems.

Key words： rotor dynamics；component mode synthesis；multi?stage modal reduction；modal reduction；structural optimization of components