谷神星一号运载火箭的时变模态参数辨识

马志赛 丁千 刘百奇 刘建设 张军锋 董威利

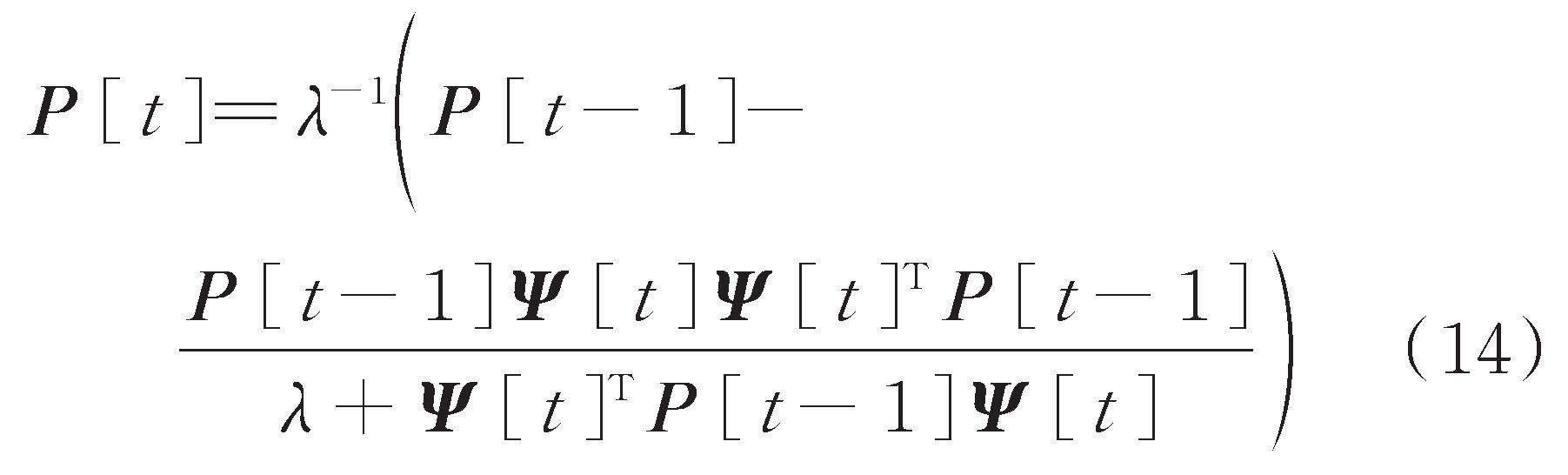
摘要： 针对运载火箭这一大型复杂系统，单纯依靠机理分析难以建立能够精确描述其时变特征的动力学模型，借助模态辨识技术获取其在飞行状态下的时变动力学特性尤为必要。面向运载火箭的飞行模态辨识需求，发展基于时变自回归滑动平均模型的仅输出递推辨识方法，引入指数加权遗忘机制进行时变特性跟踪，能够在激励未知的情况下仅基于响应数据准确快速辨识运载火箭的时变模态。以谷神星一号运载火箭为例，开展飞行遥测数据的快速处理，准确辨识发射准备阶段和飞行阶段的关键低阶时变模态，辨识结果与有限元分析结果的变化规律相互吻合，验证了所提时变模态仅输出递推辨识方法是有效可行的，服务了运载火箭有限元模型修正和姿控系统设计的实际工程需求。

关键词： 运载火箭； 时变模态参数； 谷神星一号； 递推辨识

中图分类号： V475.1； O327    文献标志码： A    文章编号： 1004-4523（2024）05-0729-08

DOI： 10.16385/j.cnki.issn.1004-4523.2024.05.001

引  言

太空探索是世界强国为提升综合国力、抢占科技制高点、保持核心竞争力而大力发展的战略性新兴产业。航天器进入太空的过程需要借助运载器来克服地球引力，新一代运载火箭追求更高的运载效率，其尺寸与推力不断增大，面临的发射与运行环境愈加恶劣，结构系统设计难度日益增加。例如，针对运载火箭这一大型复杂系统，单纯依靠机理分析难以建立能够精确描述其时变特征的动力学模型，仍需要依靠模态辨识技术来获取其真实飞行状态下的时变动力学特性。因此，为更好地满足航天工程高可靠、低成本和快速响应的发射需求，从结构动力学反问题入手，开展运载火箭时变模态参数辨识的关键技术攻关和方案深化论证，对解决运载火箭的相关动力学与控制问题意义重大［1?3］。

由于燃料快速消耗和级间分离，飞行状态下的运载火箭会表现出显著的时变特征，准确获取其时变模态对姿控系统设计、动载荷设计、天地差异研究和系统优化设计等都具有重要意义［2?6］。以姿控系统设计为例，运载火箭主要依靠陀螺敏感姿态进行控制以实现稳定飞行。在实际飞行中，陀螺感受到的姿态信息不仅包含刚体姿态，还包含箭体弹性变形所引起的附加姿态，姿控系统的设计必须考虑弹性振动的影响，否则可能会导致姿态发散，飞行失败［2?3，7］。然而为了保证良好的气动特性与运载效率，运载火箭常常呈现出长细比大、结构质量占比低的特点，导致其弹性振动频率接近刚体穿越频率且具有较宽的变化范围，在扩大陷波滤波器凹陷宽度的同时，还需要增加相位稳定方案。例如，Ares?I运载火箭的长细比约为17，其一级火箭结构的一阶弯曲模态低至0.9 Hz，与一级火箭PID控制器的带宽非常接近［8］，燃料快速消耗会导致固有频率不断发生变化，大大增加了姿控系统的设计难度［9］。此外，以往飞行试验的遥测数据表明，由于无法准确模拟飞行状态下运载火箭的真实工作环境，通过有限元分析或地面振动试验获得的模态参数往往与飞行状态下的真实值存在一定差异，这进一步增加了姿控系统的设计难度［10?12］。因此，充分利用天地试验数据和模态辨识理论发展运载火箭时变模态辨识技术，将是未来实现运载火箭弹性振动智能控制与实时决策的必经途径。

近十年来，随着辨识理论与测试技术的不断发展，工作模态分析在航天领域已取得一定进展。James等［13?14］对运载火箭工作模态分析方法进行了综述，并指出时变的系统特性、非定常的运行环境及其所导致的非平稳振动响应，是解决运载火箭时变模态辨识问题的主要挑战。De Vivo等［5］基于欧空局Vega火箭的飞行数据，采用自然激励技术（NExT）生成相关函数，在短时时不变假设下采用最小二乘复指数法估计模态参数，与有限元分析结果吻合良好。张家雄等［15］采用PolyMAX方法对飞行器低空飞行试验中典型部位的低频振动实测数据进行辨识，将模态辨识结果与地面振动试验进行对比，发现两者固有频率接近，模态振型基本吻合，但也存在一定偏差。针对飞行遥测数据信噪比低、辨识结果虚假模态多的问题，王亮等［16?17］将自回归滑动平均（ARMA）方法与NExT相结合用于飞行模态辨识，并基于稳定图对真实模态进行了筛选。随后王亮等［6］又研究了特征时段选择对飞行模态辨识结果的影响，指出在使用遥测数据进行模态辨识时，应选择低阶模态响应信噪比较高的数据段。南宫自军等［2］以Ares I?X运载火箭飞行模态辨识［4］为案例，对飞行模态辨识技术的研究现状和未来发展方向进行了综述。董严等［18］采用ARMA方法对某火箭飞行试验中三个测点的实测数据进行辨识，得到了其横向模态参数随时间的变化规律。马志赛等［19］对子空间方法、时间序列方法等时域辨识方法进行了系统性总结，指出在复杂噪声环境下开展在线、自适应时变模态辨识及其工程应用是未来的发展重点。Ma等［20?21］基于时变自回归滑动平均（TARMA）模型提出了一系列时变模态仅输出递推辨识方法，并搭建大长细比变质量充液筒试验平台，完成了辨识方法的实验验证，为开展运载火箭飞行模态辨识奠定了基础。余磊等［22］发展了一种基于TARMA模型的时变模态批量辨识方法，并利用Ariane?5运载火箭芯级的数值仿真数据对所提方法进行了数值验证。马庆港等［3］对运载火箭工作模态辨识方法及流程进行了综述，指出准确获取模态参数对运载火箭有限元模型修正、自适应控制、实时状态监测等均具有重要意义。

随着运载火箭重量、推力和长细比的进一步增大，其振动特性愈加复杂，固有频率呈现出低且密集的特点，具有显著时变特性的结构系统与控制、气动、动力等分系统之间的耦合问题也日渐突出。为获取谷神星一号运载火箭的全周期模态信息，本文旨在发展适用于运载火箭的时变模态仅输出递推辨识方法，以期在激励未知的情况下，仅基于响应数据辨识运载火箭的飞行模态。在此基础上，借助递推辨识方法计算量和所占用内存空间较小，以及对计算机的处理能力和存储空间要求较低的优势，开展谷神星一号运载火箭飞行遥测数据的快速处理，准确辨识其主要低阶飞行模态，服务相关系统设计需求。

1 谷神星一号运载火箭

1.1 发射记录

谷神星一号运载火箭是中国民营航天企业北京星河动力装备科技有限公司自主研发的一款四级小型固体商业运载火箭，一、二、三级采用固体发动机，四级为液体上面级。该运载火箭直径1.4 m，全长约20 m，起飞重量约33 t，500 km太阳同步轨道运载能力为300 kg，可满足微小型卫星的专属、共享、搭载等定制化发射需求。如图1所示，谷神星一号运载火箭的发射记录已有5次。

2020年11月7日，谷神星一号（遥一）运载火箭在酒泉卫星发射中心发射，成功将天启星座十一星精确送入预定轨道。这是星河动力实施的首次发射任务，也是中国民营商业运载火箭首次进入500 km太阳同步轨道，是中国商业航天的一次重大突破。

2021年12月7日，谷神星一号（遥二）运载火箭成功发射，将搭载的5颗小卫星送入预定轨道，首次实现“一箭五星”。2022年8月和11月，谷神星一号（遥三、四）运载火箭接连发射两次，将多颗卫星顺利送入预定轨道。2023年1月9日，谷神星一号（遥五）运载火箭在酒泉卫星发射中心发射，再次将搭载的5颗卫星顺利送入预定轨道。截至目前，该型火箭保持着100%的发射成功率，不断刷新纪录，正式进入快响应、高密度的规模化发射阶段。

1.2 时变模态辨识问题

谷神星一号运载火箭为三级固体发动机加先进液体上面级，如图2所示。其中，芯一级配备单台固体发动机，海平面推力为60 t，燃烧时间为74 s；芯二级配备单台固体发动机，推力为28 t，燃烧时间为70 s；芯三级配备单台固体发动机，推力为8.8 t，燃烧时间为69 s。一、二级级间采用热分离方式，分离时间短，二级飞行初始稳定性好。

发动机燃料快速消耗和级间分离会引起运载火箭自身质量分布的显著变化，进而导致飞行状态下运载火箭的模态参数（固有频率、阻尼比、模态振型等）不断变化。显然，姿控等分系统的设计均需要根据运载火箭实时的模态参数进行调整，因此，能否准确快速获取飞行状态下运载火箭的时变模态，对各分系统设计至关重要。

随着测试技术（数据采集与传输、传感器布局优化等）水平、新型传感器性能以及计算机处理能力的不断提升，开展运载火箭飞行模态辨识所需的硬件条件已基本成熟，制约该技术走向实用化的主要障碍在于欠缺高效鲁棒的辨识方法。除响应信号的非平稳性、辨识信息的低冗余度、短数据甚至实测数据不完整等一般性问题外，开展运载火箭飞行模态辨识的主要挑战表现在以下三个方面［19］：

（1） 仅输出。运载火箭在飞行状态下才会表现出时变特性，而飞行状态下作用在结构上的激励难以观测（如气动载荷、发动机内部扰动等），施加可控可测的人工激励难度较高。因此，解决运载火箭飞行模态辨识问题需要首先解决仅输出辨识问题，即在激励未知的情况下，仅基于响应数据获取运载火箭的时变模态。

（2） 递推。为实现在线监测与实时控制，需要对运载火箭的时变特性进行快速获取，这就要求辨识方法具有可递推性，即在采集得到当前时刻新数据后，只基于新数据所提供的信息去修改原来估计出的模态参数，而不是基于所有数据重新进行一轮模态参数估计。递推辨识过程中每一步的计算量和所占用的内存空间较小，对计算机的处理能力和存储空间要求较低，可保证数据处理过程跟得上数据采集过程。

（3） 复杂噪声。由于激励未知，从处理实测响应数据的难易程度来看，运载火箭真实的发射与运行工况远比地面振动试验更为恶劣，需要经历复杂的噪声环境。例如，当环境激励较弱时，箭体结构弹性振动幅值较小，可能导致实测响应信号的信噪比较低，甚至淹没在环境噪声中。动量轮等姿控器件、发动机内部燃烧、液体晃动、旋转部件等因素会产生谐波激励，导致作用在箭体上的激励为非白噪声，基于有色噪声激励下的响应信号进行时变模态辨识常常会出现虚假模态。此外，当实测响应信号中含有脉冲噪声等不满足高斯分布的测量噪声时，也会严重影响数据质量，甚至导致辨识结果失真。

综上所述，发展运载火箭时变模态仅输出递推辨识方法，在同时满足“仅输出”和“递推”的基础上兼顾解决“复杂噪声”问题，是运载火箭飞行模态辨识技术最终走向实用化的必经之路。

2 仅输出递推辨识方法

2.1 时变自回归滑动平均模型

由于运载火箭自身显著的时变特性，其响应信号具有非平稳性，时域信号随时间的变化规律是运载火箭结构系统时变特性的最直接体现。相较于频域辨识方法，时域辨识方法无需将非平稳的响应信号变换至频域进行分析，可有效避免数据变换过程中的各类误差［19］。此外，频域辨识方法难以满足递推辨识需求，因此，目前常用的仅输出递推辨识方法主要基于状态空间模型或时间序列模型发展而来［19，23］。本节主要介绍时间序列模型中的时变自回归滑动平均（TARMA）模型，进而给出基于TARMA模型的仅输出递推辨识方法。

作为基于非平稳时间序列建立起来的离散模型，TARMA 模型既能反映时间序列自身数据结构及其变化规律，也能反映产生该时间序列的待辨识系统的固有特性。令na 和nc 分别表示自回归和滑动平均阶数，则TARMA 模型可写为如下形式［19，23］：

式中 x [ t ] 表示维度为k 的离散非平稳响应信号；e [ t ] 表示均值为零、协方差为Σ [ t ] 的不相关残差序列，即满足正态独立分布N （ 0，Σ [ t ] ）；Ai [ t ] 和Ci [ t ] 分别表示TARMA 模型的自回归和滑动平均系数矩阵。

基于“时间冻结”假设，可得每一时刻TARMA模型的功率谱密度（Power Spectral Density，PSD）函数为［23?25］：

式中 ω 表示频率，单位为rad s；Δt 为采样间隔；j 为虚数单位；（ ? ） H 表示矩阵的Hermitian 转置。

每一时刻TARMA模型的模态参数可通过求解如下特征值问题获得［23?24］：

（ pi [ t ] I - A [ t ]） vi [ t ]= 0， i= 1，2，…，kna   （3）

式中 pi [ t ]和vi [ t ]=[ pi [ t ]-na LTi，…，pi [ t ]-1 LTi]T分别表示伴随矩阵A [ t ] 的特征值和特征向量，其中Li 为模态振型向量；I 为单位矩阵。伴随矩阵A [ t ]由自回归系数矩阵构成，具体如下［23?24，26］：

更进一步，可得TARMA模型的固有频率和阻尼比分别如下：

时间序列x [ t ] 的取值大小与先后顺序反映了待辨识系统的固有特性，因此，TARMA 模型参数Ai [ t ]，Ci [ t ] 和Σ [ t ] 中也蕴含了该系统固有特性的信息，这一过程可归纳为信息的凝聚性，即大量数据所蕴含的信息被凝聚为少数几个模型参数［23］。显然，在估计得到TARMA 模型参数后，即可基于上述过程获取待辨识系统的模态参数。

在TARMA模型参数的估计过程中，自回归和滑动平均阶数会直接影响估计精度及其计算复杂度。对于TARMA模型参数的递推估计过程，可根据残差特性来选择模型阶数，即通过计算残差平方和与序列平方和的比值来刻画TARMA模型对信号的拟合误差［23，27］。一般地，较高的模型阶数能够更好地对信号进行拟合，有助于减小拟合误差，而较低的模型阶数则意味着较低的计算复杂度和较好的计算效率。因此，模型阶数的选择过程往往需要在拟合精度与计算效率之间做折中。

2.2 辨识方法

将式（1）中的TARMA模型改写为伪线性回归形式［23?25］，如下式所示：

x [ t ]= w [ t ]TΨ [ t ]+ e [ t ] （6）

其中参数矩阵w [ t ] 和回归向量Ψ [ t ] 分别具有如下形式：

在TARMA 模型参数的估计过程中，需要对旧数据进行遗忘，降低旧数据对当前估计结果的影响，以有效跟踪待辨识系统的时变特性。借助指数加权遗忘机制，引入遗忘因子λ（0 < λ ≤ 1）对时刻τ 下的数据进行加权（权值为λt - τ），以实现对旧数据的遗忘。定义指数加权最小二乘费用函数如下［23］：

式中表示Euclidean范数。

式（9）的解为：

式中 diag{ ? }表示以{ ? }中元素为对角元素的对角矩阵。

定义协方差矩阵P [ t ]如下：

则进一步可得：

P [ t ]-1 = λP [ t - 1 ]-1 + Ψ [ t ] Ψ [ t ]T （13）

根据矩阵逆定理，式（13）可改写为：

将式（14）代入式（10）可得：

形式：

则式（15）中t 时刻参数矩阵的估计值w? [ t ] 可改写为：

综合式（14）～（19），可将指数加权递推伪线性回归TARMA模型参数估计方法［23］总结如下：

在估计得到参数矩阵后，基于式（2）可计算时变PSD 函数，基于式（3）～（5）可计算时变模态参数。需要说明的是，该方法的初始化条件为w? [ 0 ]T = 0和P [ 0 ]= αΙ，其中系数α 一般选取较大的正数，例如α= 104［ 23，27］，旨在保证初始状态时协方差矩阵足够大。由于指数加权遗忘机制的引入，α 对估计结果的影响会随着数据长度的增加而逐渐消失。一般地，对渐变系统进行辨识时通常选择遗忘因子λ 为常数，对于突变系统则需选择自适应的遗忘因子。

3 时变模态辨识结果

3.1 发射准备阶段

本节基于谷神星一号运载火箭的惯性器件遥测数据进行时变模态辨识。选用运载火箭横向和法向速度增量的遥测数据，开展基于多分量实测非平稳振动信号的数据快速处理与时变模态辨识。在点火发射前，运载火箭竖立于发射台上，可近似视为悬臂梁边界条件，由于发动机尚未点火，此时其模态参数应保持不变。为验证该阶段运载火箭的模态参数是否发生变化，在选择TARMA 模型阶数na = 20 和nc = 2 的情况下，进一步选取遗忘因子λ = 0.984，基于点火发射前90 s 内的遥测数据对运载火箭的固有频率和PSD 函数进行辨识，获取地面风载作用下运载火箭模态参数随时间的变化规律。

发射准备阶段固有频率的辨识结果如图3所示，其中，红色圆点为固有频率的辨识结果，绿色虚线为有限元模型计算得到的固有频率参考值。由图3可知，在发射前90 s内，运载火箭的前三阶固有频率基本保持不变，这与实际工况是一致的。发射准备阶段PSD函数的辨识结果如图4所示，显然图中脊线均呈现水平状态，且与图3中固有频率的辨识结果完全对应，这也进一步表明该阶段运载火箭的模态参数基本保持不变。需要说明的是，从发射前60 s开始，运载火箭的电爆阀、隔离阀等相继开始工作，相应的起爆和开启动作会引起较大的冲击振动，因此图4中相继出现了多条竖直方向的高亮谱线，也导致了图3中相对应时刻的固有频率辨识结果较差。

将图3中的固有频率辨识结果与有限元计算结果进行对比，发现前两阶固有频率吻合良好，但有限元计算出的第三阶固有频率值较辨识值偏高。前期相关研究已表明，基于Ares I?X和Vega火箭的有限元模型计算得到的固有频率常常与其辨识值存在偏差［3?5］，这也进一步说明了有限元模型与真实工作状态下的运载火箭仍存在差异。因此，为更好地对谷神星一号运载火箭的结构动力学特性进行表征，尤其是对发射准备阶段第三阶模态进行表征，仍需要对其有限元模型进行修正，以提高模型精度。

3.2 飞行阶段

如图2所示，谷神星一号运载火箭芯一级所配备的固体发动机的燃烧时间为74 s。因此，基于运载火箭点火发射后0～74 s的遥测数据可对一级飞行阶段的模态参数进行辨识。固有频率及其对应PSD函数的辨识结果如图5所示，其中，红色圆点为固有频率的辨识结果，背景色为PSD函数的辨识结果。由图5可知，固有频率的辨识结果与PSD函数的脊线吻合良好，清晰表明前四阶固有频率均随燃料消耗而不断升高，验证了本文辨识方法对运载火箭时变模态进行跟踪的有效性。需要说明的是，由于发射40 s之后第二阶模态未被较好地激发出来，导致第二阶固有频率的辨识精度较差，但PSD函数的脊线依旧能够刻画出第二阶固有频率的大概变化规律。

此外，图5中也给出了芯一级固体发动机满载和空载情况下基于有限元模型计算得到的固有频率参考值，分别对应实际飞行的0时刻和74 s时刻，在图5中用黑色菱形表示。显然，飞行模态的辨识结果和有限元计算结果吻合良好，说明本文辨识方法能够对运载火箭的时变模态进行准确辨识。需要指出的是，在火箭发动机满载和空载情况下进行有限元分析相对容易，但在有限元模型中考虑燃料消耗所导致的质量连续时变特性比较困难，难以获取每一时刻下运载火箭的模态信息。因此，开展飞行模态辨识可有效弥补有限元分析的这一局限性，能够连续获取每一时刻下运载火箭的模态参数，为姿控系统设计和天地一致性研究提供重要支撑。

如图2所示，谷神星一号运载火箭芯二级所配备的固体发动机的燃烧时间为70 s。因此，基于运载火箭点火发射后75～145 s的遥测数据可对二级飞行阶段的模态参数进行辨识。固有频率及其对应PSD函数的辨识结果如图6所示。由图6可知，固有频率的辨识结果与PSD函数的脊线吻合良好，表明了前两阶固有频率均随燃料消耗而不断升高的规律。与图5中的辨识结果相比，图6中模态辨识结果的精度相对较差，主要是由于二级飞行阶段运载火箭的飞行速度更大，所处噪声环境更为复杂，一定程度上增加了仅基于响应数据进行模态辨识的难度。此外，图6中25～30 Hz频带内虽然模糊出现了PSD函数的脊线，但在辨识过程中通过筛除阻尼比过大的极点，该频带内并未出现大范围的虚假模态。

类似地，图6中也给出了芯二级固体发动机满载和空载情况下基于有限元模型计算得到的固有频率参考值，分别对应实际飞行的75 s时刻和145 s时刻。由图6可知，飞行模态的辨识结果和有限元计算结果基本吻合，说明本文辨识方法依旧能够对运载火箭二级飞行阶段的时变模态进行跟踪。

目前，通过有限元分析和地面振动试验，一般在运载火箭发射之前就给定了其整个工作周期的模态特性，但两者均难以连续获取运载火箭的时变模态参数。有限元方法难以对连续时变结构系统进行仿真分析，只能对特定时刻（或特定燃料消耗情况）下的结构系统进行模拟。地面振动试验无法避免进行多次重复试验的繁琐流程，往往采用秒时刻冻结进行多次时不变结构系统的模态试验，再利用插值法获取全过程的模态信息，费时费力。相较而言，借助时变模态辨识技术，充分利用天地试验数据，可准确快速地获取真实工作状态下运载火箭的时变动力学特性，且满足天地一致性要求，能够有效服务运载火箭的有限元模型修正和姿控系统设计。

4 结  论

本文系统性介绍了运载火箭时变模态辨识的研究意义和发展现状，阐述了现阶段开展时变模态辨识所面临的难题与挑战，发展了指数加权递推伪线性回归TARMA模型参数估计方法，能够在激励未知的情况下，仅基于响应数据快速辨识运载火箭的时变模态。在工程应用方面，围绕谷神星一号运载火箭的时变模态辨识问题，基于上述辨识方法完成了飞行遥测数据的快速处理，准确辨识了发射准备阶段和飞行阶段的关键低阶时变模态，有效服务了运载火箭的有限元模型修正和姿控系统设计。

参考文献：

［1］      孟光， 周徐斌， 苗军. 航天重大工程中的力学问题［J］. 力学进展， 2016， 46： 267-322.

MENG Guang， ZHOU Xubin， MIAO Jun. Mechanical problems in momentous projects of aerospace engineering［J］. Advances in Mechanics， 2016， 46： 267-322.

［2］      南宫自军， 戴新进， 王亮， 等. 航天飞行器飞行模态辨识技术应用及展望［J］. 强度与环境， 2017， 44（1）： 20-26.

NANGONG Zijun， DAI Xinjin， WANG Liang， et al. Application and prospective outlook of the aerospace vehicles operational mode identification［J］. Structure & Environment Engineering， 2017， 44（1）： 20-26.

［3］      马庆港， 王紫扬， 康杰， 等. 运载火箭结构工作模态参数辨识研究综述［J］. 弹箭与制导学报， 2022， 42（1）： 60-70.

MA Qinggang， WANG Ziyang， KANG Jie， et al. Overview of operational modal parameter identification for structures of rocket launchers［J］. Journal of Projectiles， Rockets， Missiles and Guidance， 2022， 42（1）： 60-70.

［4］      Bartkowicz T J， James G H. Ares I-X in-flight modal identification［C］. 52nd AIAA/ASME/ASCE/AHS/ASC Structare， Structural Dynamics and Materials Conference. Denver， Colorado， 2011.

［5］      De Vivo A， Brutti C， Leofanti J L. Vega in-flight modal identification with the operational modal analysis technique［J］. Journal of Spacecraft and Rockets， 2014， 51（5）： 1464-1473.

［6］      王亮， 张妍， 蔡毅鹏， 等. 特征时段选择对飞行模态辨识结果的影响［J］. 噪声与振动控制， 2017， 37（1）： 128-131.

WANG Liang， ZHANG Yan， CAI Yipeng， et al. Influence of the measure feature phase selection on operational modal identification of aircrafts［J］. Noise and Vibration Control， 2017， 37（1）： 128-131.

［7］      Khoshnood A M， Roshanian J， Jafari A A， et al. Simultaneous estimation of two bending vibration frequencies for attitude control of a flexible launch vehicle［J］. Journal of Systems and Control Engineering， 2009， 223： 721-726.

［8］      Jang J W， Hall R， Bedrossian N， et al. Ares-I bending filter design using a constrained optimization approach［C］//AIAA Guidance， Navigation and Control Conference and Exhibit. Honolulu， Hawaii， 2008： 6289.

［9］      Tobbe P A， Matras A L， Wilson H E. Modeling and simulation of variable mass， flexible structures［C］//AIAA Modeling and Simulation Technologies Conference. Chicago， Illinois， 2009： 6023.

［10］    Fransen S， Rixen D， Henriksen T， et al. On the operational modal analysis of solid rocket motors［C］//The 28th IMAC， International Modal Analysis Conference. Jacksonville， Florida， 2010： 453-463.

［11］    Goursat M， D?hler M， Mevel L， et al. Crystal clear SSI for operational modal analysis of aerospace vehicles［C］//The 28th IMAC， International Modal Analysis Conference. Jacksonville， Florida， 2010： 1421-1430.

［12］    Manzato S， Peeters B， Debille J. Tracking the evolution of modal properties of a solid propellant launcher during static firing test［C］//The 30th IMAC， International Modal Analysis Conference. Jacksonville， Florida， 2012： 559-570.

［13］    James G H. Development of operational modal analysis techniques for launch data［J］. Advances in the Astronautical Sciences， 2013， 147： 209-230.

［14］    James G， Kaouk M， Cao T. Progress in operational analysis of launch vehicles in nonstationary flight［C］//The 31st IMAC， International Modal Analysis Conference. Garden Grove， California， 2013： 59-75.

［15］    张家雄， 何咏梅， 张华山， 等. 基于PolyMAX法的飞行器工作模态分析技术与应用［J］. 航天器环境工程， 2015， 32（1）： 28-33.

ZHANG Jiaxiong， HE Yongmei， ZHANG Huashan， et al. Operational modal analysis technology based on PolyMAX method and its applications for flying vehicles［J］. Spacecraft Environment Engineering， 2015， 32（1）： 28-33.

［16］    王亮， 张妍， 周晓丽， 等. 基于ARMA-NExT和稳定图方法的飞行器工作模态指示研究［J］. 动力学与控制学报， 2016， 14（3）： 258-262.

WANG Liang， ZHANG Yan， ZHOU Xiaoli， et al. Study on the indication of the aircraft operational mode based on ARMA-NExT and stabilization diagram［J］. Journal of Dynamics and Control， 2016， 14（3）： 258-262.

［17］    王亮， 蔡毅鹏， 朱辰， 等. 基于ARMA-NExT的飞行器工作模态辨识技术研究［J］. 导弹与航天运载技术， 2017（1）： 18-21.

WANG Liang， CAI Yipeng， ZHU Chen， et al. Operational mode identification of the aircraft based on ARMA-NExT［J］. Missiles and Space Vehicles， 2017（1）： 18-21.

［18］    董严， 付小燕， 丁志伟. 基于多测点数据的火箭飞行模态参数识别方法［J］. 固体火箭技术， 2018， 41（4）： 520-523.

DONG Yan， FU Xiaoyan， DING Zhiwei. Rocket flight modal identification method based on data of multi-measure points［J］. Journal of Solid Rocket Technology， 2018， 41（4）： 520-523.

［19］    马志赛， 丁千， 刘莉， 等. 线性时变结构模态参数时域辨识方法的研究进展［J］. 机械工程学报， 2018， 54（23）： 137-159.

MA Zhisai， DING Qian， LIU Li， et al. Research progress on time-domain modal parameter estimation methods for linear time-varying structures［J］. Journal of Mechanical Engineering， 2018， 54（23）： 137-159.

［20］    Ma Z S， Ding Q， Tang Y. Operational modal analysis of a liquid-filled cylindrical structure with decreasing filling mass by multivariate stochastic parameter evolution methods［J］. International Journal of Mechanical Sciences， 2020， 172： 105420.

［21］    Ma Z S， Li L Q， Ding Q. Multivariate recursive bayesian linear regression and its applications to output-only identification of time-varying mechanical systems［J］. Journal of Vibration and Control， 2021， 27（11-12）： 1395-1406.

［22］    余磊， 刘莉， 崔颖， 等. 一种运载火箭时变结构模态参数辨识的确定性演化方法［J］. 宇航学报， 2020， 41（4）： 379-388.

YU Lei， LIU Li， CUI Ying， et al. A time-varying structure modal parameter estimation method in deterministic evolution for launch vehicle［J］. Journal of Astronautics， 2020， 41（4）： 379-388.

［23］    马志赛. 线性时变结构模态参数仅输出递推辨识方法研究［D］. 北京： 北京理工大学， 2017.

MA Zhisai. Output-only modal parameter recursive estimation for linear time-varying structures［D］. Beijing： Beijing Institute of Technology， 2017.

［24］    Ma Z S， Liu L， Zhou S D， et al. Parametric output-only identification of time-varying structures using a kernel recursive extended least squares TARMA approach［J］. Mechanical Systems and Signal Processing， 2018， 98： 684-701.

［25］    Ma Z S， Ding Q， Zhou S D. Novel adaptive methods for output-only recursive identification of time-varying systems subject to gross errors［J］. Journal of Vibration and Control， 2020， 26（5-6）： 306-317.

［26］    Bertha M， Golinval J C. Identification of non-stationary dynamical systems using multivariate ARMA models［J］. Mechanical Systems and Signal Processing， 2017， 88： 166-179.

［27］    Spiridonakos M D， Fassois S D. Parametric identification of a time-varying structure based on vector vibration response measurements［J］. Mechanical Systems and Signal Processing， 2009， 23（6）： 2029-2048.

Time-varying modal parameter estimation of the CERES-1 launch vehicle

Abstract： It is usually difficult to establish the dynamic model of a launch vehicle that accurately describes its time-varying characteristics. Therefore modal identification techniques are particularly necessary to obtain the time-varying dynamic characteristics of launch vehicles under flight conditions. Aiming at the problem of in-flight modal identification of launch vehicles， an output-only recursive identification method based on the time-dependent autoregressive moving average model is developed by using exponentially weighted mechanisms to track the time-varying characteristics. Without measuring the natural excitation forces， the proposed method can accurately and quickly identify the time-varying modal parameters of launch vehicles by exclusively using the measured response signals. Taking the CERES-1 launch vehicle as an example， time-varying modal parameters before liftoff and during the flight phase are accurately estimated by processing the flight telemetry data. Identification results are consistent with the variation of the finite element analysis results， demonstrating the high achievable accuracy of the proposed method. The proposed in-flight modal identification method can obtain the full-cycle modal information of launch vehicles， which meets the engineering requirements for the finite element model updating and attitude control system design.

Key words： launch vehicle； time-varying modal parameter； CERES-1； recursive identification