基于接触单元的穿越施工管线变形数值模拟方法

摘要 新建盾构隧道穿越施工将引起既有地下管线产生变形，在采用数值模拟方法进行管线变形计算时可采用接触单元模拟管土相互作用，但现有方法未对接触单元计算参数的选取进行讨论，不能保证计算结果的可靠性。文章采用有限元软件Ansys对新建盾构隧道穿越既有地下管线的数值模拟方法进行了研究，其中，管线与土体的相互作用通过接触单元进行模拟。为选择合适的接触单元计算参数，对管线与土体复杂的接触问题进行了力学简化，分析了有限元软件中接触刚度与工程中常见力学参数的联系，给出了接触刚度的试算过程及其他接触单元计算参数的选取依据。将管线变形和弯矩计算结果与既有文献中理论计算结果及离心模型试验数据进行了对比，并选取实际工程进行了案例计算。

关键词 数值模拟；接触单元；盾构隧道；地下管线；管土相互作用

中图分类号 U455文献标识码 A文章编号 2096-8949（2024）08-0001-04

0 引言

隧道开挖引起的管线变形问题为管线与土层的相互作用问题，数值模拟能够较为真实地反映管土相互作用，且能直观地模拟隧道开挖与支护的过程，相较于模型试验又具有成本较低的优点，在学术界及工程界得到大量应用[1-5]。

目前管土相互作用的有限元模拟方法主要包含三种类型：一类是地基弹簧，其中弹簧一端与管线单元共用节点，另一端施加土体位移荷载；一类是采用Abaqus中的管土相互作用单元，需土体位移荷载作为模型的输入数据；最后一类为接触单元，能够较为全面地模拟管线与土体之间法向、切向的相对运动与力学行为。根据现有的大多数研究报道可知，在使用接触单元模拟管土相互作用时，一般采用软件默认的接触单元计算参数，并未对接触单元的参数选取进行讨论，也未实现接触单元计算参数与常用管土相互作用参数的对应。

该文采用接触单元模拟管土相互作用，建立了隧道穿越既有管线的有限元模型。为选择合适的接触单元计算参数，通过研究地基系数与接触刚度的关系，给出了接触刚度的试算过程，并详细介绍了其他接触单元计算参数的选取依据。依托实际工程施工参数进行了案例计算，对该文方法的正确性进行了验证。

1 模型建立

1.1 模型假设

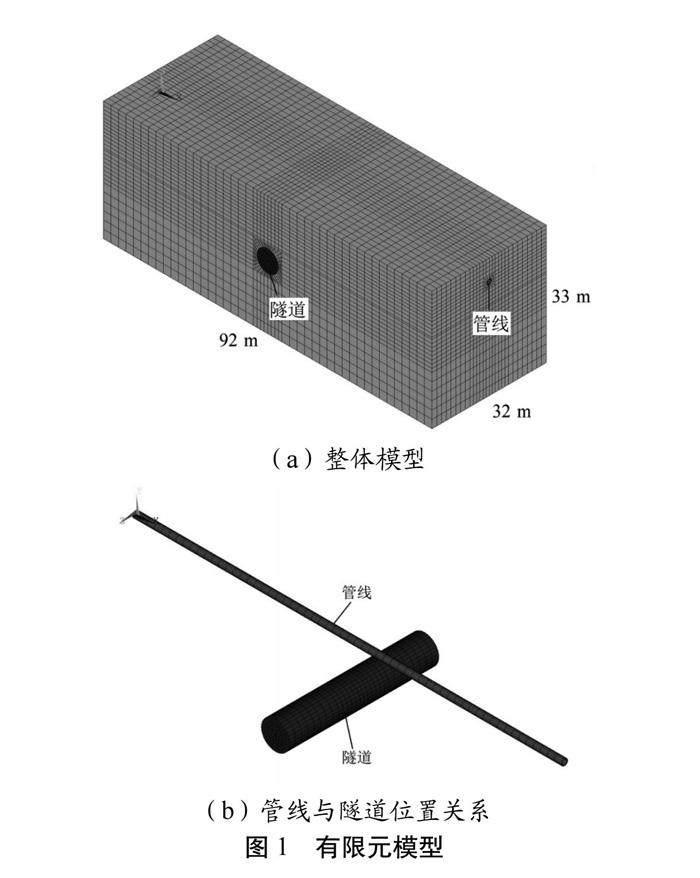
采用Ansys软件建立隧道穿越既有管线模型，有限元模型尺寸参考程霖[6]所述离心模型试验原型尺寸（92 m×32 m×33 m）。如图1所示。

土体和管线均采用实体单元SOLID185进行网格划分，管土界面相互作用采用接触单元CONTA173和目标单元TARGE170建立接触进行模拟。

1.2 接触单元的生成规则

接触面与目标面通过摩擦传递切线作用力，通过“侵入”传递法向作用力，且接触面不能侵入目标面，而反之则可以，故而可选较硬的面作为目标面，较软的面作为接触面。根据管线与土体的材料性质，将土体内表面作为接触面，建立接触单元CONTA173，管线外表面作为目标面，建立目标单元TARGE170。Ansys软件通过识别相同编号的实常数，自动识别目标单元与接触单元并建立接触对。

2 计算参数

2.1 土体和管线参数

该文采用EDP模型进行土体材料模拟，EDP模型包含2个计算参数，分别是屈服参数σye和压力敏感参数αp，可通过土体内摩擦角φ和内黏聚力c进行推导，即：

（1）

（2）

EDP模型流动法则计算参数参照式（1）进行推导，但需要用剪胀角ψ代替内摩擦角φ。该文剪胀角取值为内摩擦角的1/2，按非关联流动法则进行计算[7]。土体和管线的计算参数见表1。

2.2 接触单元参数

对于该文所研究的管线与土体相互作用问题，管土法向接触刚度、切向接触刚度、法向容许侵入量、管土界面黏结力、管土摩擦系数为关键计算参数，关系到管线变形与受力计算的准确性。

2.2.1 接触刚度

在Ansys中，接触刚度包含法向接触刚度（FKN）与切向接触刚度（FKT），其与地基系数量纲一致（FL-3），但由于力学原理不同，两者有不同的取值，下面给出通过地基系数确定接触刚度的简便试算方法。

计算简图如图2所示，当管土产生相对位移时，假设管线截面形状不发生改变，对于管线与土体竖向相对运动，假设管线在荷载作用下横截面不发生形变。图2（a）为管土发生相对位移后，管线的受力情况，其中，α为任意圆心角，δv为管土竖向相对位移，pn、pf为管线受到的法向荷载和切向荷载，D为管线外径。图2（b）为有限元计算过程中管线（目标面）与土体（接触面）相互侵入示意图，在有限元模型中，管土相互侵入量小于管线位移，将最大侵入量与管线竖向位移的比值记为参数ζ。

根据图2的几何关系，令接触单元FKN和FKT分别为fN和fT，则管线所受地基反力可表示为：

（3）

式中，α0=arcsin（ζδv/D）；δh——管土相对切向位移。

根据Winkler地基模型，管线所受地基反力还可表示为：

PR=KvDδv （4）

式中，Kv——基于Winkler地基模型的地基系数。

比较式（3）和式（4），可得：

（5）

根据式（5），结合室内加载试验对接触刚度进行试算，试算步骤：

（1）按室内加载试验测得地基系数（包括竖向与切向）定义有限元软件中FKN和FKT初始值。

（2）对图1管线模型施加室内加载试验所得管线极限位移，计算得到的管线所受竖向地基反力及接触单元最大侵入量，通过最大侵入量与管线竖向位移的比值计算参数ζ。

（3）根据式（5）调整FKN取值，并反复进行有限元计算，使计算所得管线竖向地基反力与加载试验测得的极限荷载一致；FKN取值确定后，采用以上思路对FKT进行试算。

2.2.2 最大容许侵入量

在Ansys中最大容许侵入量采用参数FTOLN表示，取值分为正值与负值：取正值时FTOLN为比例系数，默认值为0.1；取负值时FTOLN的绝对值为最大容许侵入量的实际数值。该文计算模型取FTOLN为室内加载试验测得管线竖向极限位移。

2.2.3 摩擦系数和管土界面黏结力

在Ansys中，接触单元界面黏结力和摩擦系数分别用COHE和MU表示。接触单元的切向摩擦符合库伦模型，当摩擦力超过库伦模型规定的等效剪应力时，接触界面发生相对滑动。该文计算模型令管土摩擦系数为0，取室内试验[6]测得的管土切向极限荷载作为管土界面黏结力。

2.2.4 单元关键字

有限元模型划分网格单元后，目标单元与接触单元的节点坐标没有完全重合，存在初始间隙或初始侵入，可能导致位移约束不良进而影响结果收敛。为此，该文对CONTA173单元的第5项关键字选取选项1，选取第9项关键字选项1，将模型建立引起的初始间隙和初始侵入消除。

根据以上讨论，将该文接触单元计算参数总结如表2所示。

3 计算过程

采用位移控制法[4]模拟隧道开挖以及开挖过程引起的地层损失，首先定义荷载步，分步进行隧道开挖，如图3所示。

对开挖面范围内土体单元节点施加位移荷载，所施加节点位移采用隧道开挖后断面的“非均匀收敛”模式进行计算，如图4所示，图中uh、uv分别为隧道水平向收敛和竖向收敛；gca为拱顶最大沉降，可采用式（6）计算：

（6）

式中，RT——隧道开挖时的半径；ε0——隧道开挖收敛断面与开挖断面面积的比率，即地层损失率。

采用式（7）、式（8）计算隧道收敛位移，并作为节点位移荷载施加在有限元模型相应位置处。

（7）

（8）

4 案例计算

4.1 方法验证

取程霖[6]所述离心模型试验的实际地层损失率，即6.89%进行计算，如图5所示，给出了管线沉降和弯矩的计算结果，并与程霖[6]相关试验及理论计算结果进行了对比。

由图5可知，在隧道中线处，该文方法管线沉降和弯矩计算结果与试验及理论计算结果能够较好地符合，证明了该文计算方法的正确性。

在距离隧道中线较远区域，该文方法计算结果与试验及理论计算结果存在较明显的差距，这是因为理论方法中地层位移是基于Peck曲线拟合所得，与数值模拟计算的地层位移有一定差异。

4.2 实例计算

成都地铁18号线某区间盾构隧道垂直下穿DN1000混凝土雨水管，管线外径1.2 m，管壁厚度0.1 m，埋深3.2 m，隧道埋深25.74 m，隧道直径为8.4 m。

按该文所述方法建立模型，土体弹性模量55 MPa，密度1 956 kg/m3，泊松比0.3，内摩擦角32.6 °，黏聚力20 kPa。管线弹性模量30 GPa，密度2 360 kg/m3，泊松比0.3，地层损失率1.4%。结合2.2节所述试算方法，管土界面接触单元法向接触刚度为9.69×107 Pa/m，切向接触刚度为8.09×106 Pa/m。

如图6所示，给出了管线沉降数值模拟结果与实测数据的对比。可见，管线变形计算值与实测值较为符合。

图6 实测数据与数值模拟结果的对比

5 结论

该文采用Ansys软件建立了隧道穿越既有管线有限元模型，使用接触单元模拟管土相互作用。通过简化管线与土体相互作用力学模型，建立了接触刚度与工程实际参数中竖向地基系数与切向地基系数的关系，给出了接触刚度的试算方法。详细介绍了接触单元最大容许侵入量、摩擦系数、黏结强度、单元关键字等参数的含义及取值依据。给出了基于控制位移法和单元“生死”技术的盾构隧道开挖模拟方法。

将数值模拟计算结果与既有程霖[6]离心模型试验测得数据和理论方法计算结果进行了对比，在隧道开挖中线附近，数值模拟方法所得管线变形和弯矩与理论解和试验数据相符，选取实际工点进行案例计算，管线变形计算值与实测值较为符合，证明了该文建模方法的正确性。

参考文献

[1]KLAR A， MARSHALL A M. Shell versus beam representation of pipes in the evaluation of tunneling effects

on pipelines[J]. Tunnelling and Underground Space Technology， 2008（4）： 431-437.

[2]WANG Y， SHI J W， NG C W W. Numerical modeling of

tunneling effect on buried pipelines[J]. Canadian Geotechnical Journal， 2011（7）： 1125-1137.

[3]王霆， 罗富荣， 刘维宁， 等. 地铁车站洞桩法施工引起的地表沉降和邻近柔性接头管道变形研究[J]. 土木工程学报， 2012（2）： 155-161.

[4]邵羽. 盾构双隧道施工对临近地埋管线的影响研究[D]. 南宁：广西大学， 2017.

[5]SHAO Y， DUAN Z B， LIU Y， et al. Estimating the effects of tunnelling on preexisting jointed pipelines[J]. Advances in Civil Engineering， 2019（4）： 1-12.

[6]程霖. 地铁隧道开挖引起地下管线变形的理论分析和试验研究[D]. 北京：北京交通大学， 2021.

[7]孔位学， 芮勇勤， 董宝弟. 岩土材料在非关联流动法则下剪胀角选取探讨[J]. 岩土力学， 2009（11）： 3278-3282.