“平面向量数量积的最值（范围）问题”作业设计

基金项目  2022年湖北师范大学教学改革研究项目“核心素养下高中数学课本习题的有效使用”（2022NO.01）.

【摘  要】  以“平面向量数量积的最值（范围）问题”作业设计为例，进行教材内容与课程标准分析，并结合实际学情，制订出总体作业目标、作业结构与作业题量说明，通过展现具体作业内容、作业案例分析与评价、作业反思与改进具体阐述作业设计的意图与策略.多类型、多层次、多视角地设计与评价作业，达到进一步巩固学生的数学知识、提升学生的探索能力、助力其数学核心素养发展的目的.

【关键词】  数量积；作业设计；作业目标；核心素养

作业是学生理解知识、训练技能、发展素养的重要环节，是教师了解学情、改进教学、有效教学的重要手段［1］.数学作业设计是指教师根据教学目标和数学课程标准，考虑学生的不同特点和知识能力水平，针对某一具体教学内容，通过选择重组、改编完善、自主开发等手段，为不同类型的学生设计出符合他们自身特点和需求的非教学时间需要完成的任务活动.

1  内容解析

1.1  教材内容

本节是人教版普通高中教科书·数学（必修）第二册第6.2.4节“向量的数量积”中知识点之一.教材根据学生的认知发展规律，按照知识的逻辑顺序进行编排，让学生在循序渐进中对向量更加深入地理解和认识，是向量运算对象的进一步扩充，体现了向量运算形式的不断发展，为后续向量的学习、在现实生活和物理中的应用，在其它数学内部的广泛应用奠定基础.同时，以平面图形为载体的有关数量积的最值（范围）是高考的热点之一，常以选择题、填空题的形式呈现.要深刻理解数量积的意义，从不同角度对数量积进行转化.解题思路是建立目标函数的解析式，转化为求函数（二次函数、三角函数等）的最值或应用基本不等式.同时向量兼顾“数”与“形”的双重身份，应用图形的几何性质，采用数形结合也是一种重要思路.

1.2  课标要求

作业设计要严格依据《普通高中数学课程标准（2017年版2020年修订）》，明确学情实际，重视目标落实，关注知识交汇，设置梯度层次，编选合适题量［2］.具体到本单元的课程标准要求是：通过几何直观，了解平面向量投影的概念以及投影向量的意义；会用向量方法解决简单的平面几何问题、力学问题以及其他实际问题，体会向量在解决数学和实际问题中的作用［3］.基于以上分析，确定本单元课时教学目标与教学重难点如下：

1.教學目标：掌握平面向量数量化的思路和方法，提高学生数形结合与转换化归的能力；通过题组分层训练，培养学生总结通性通法解题规律的能力.

2.教学重点：提炼平面向量数量化的两种基本思路，归纳几种常见的数量积最值（范围）问题的求法.

3.教学重点：提升学生运用数形结合与转换化归等数学思想解决问题的意识.

2  学情分析

向量既是代数研究对象，也是几何研究对象，是沟通几何与代数的桥梁.本单元是在学生已经系统地学习了平面向量的概念、运算、基本定理以及坐标表示的基础上，对平面向量在几何方面应用的研究.通过系统地学习，学生可以发现，平面几何图形的很多性质都可以用向量表示出来，许多问题都可以用向量运算的方法加以解决，体会到了平面向量作为工具研究平面几何问题的优越性.

3  作业设计说明

3.1  作业目标

（1）在不同情境的作业训练中，帮助学生加深对平面向量数量积定义的理解，提升学生数学抽象核心素养；

（2）通过不同题型的分组训练，让学生掌握多种向量数量积的最值（范围）求解策略，提升学生数学运算核心素养；

（3）让学生经历具体问题的解决，提升分析问题与解决问题的能力，提升学生数学逻辑推理核心素养.

3.2  作业结构

本次单元作业设计主要设计三类作业：基础性作业、提高性作业、拓展性作业.同时，依据题目解法类型又将作业分组：投影法、基底法、坐标法、数形结合法、极化恒等式法、探究问题六组，如图1.

3.3  作业题量

根据高考数学考试时间及试题分布，笔者认为，高中数学作业设计的题量以12题为宜：大致单选5题、多选2题、填空3题、解答2题.但是，根据本节内容的特点并结合高考对本知识点的考查要求，本次作业仅设计12道小题（选择题和填空题），以检测学生对平面数量积的最值（范围）的掌握情况，以便后期教与学的改进.

4  具体作业设计

4.1  基础性作业

第1组  投影法

1.已知P是边长为2的正六边形ABCDEF内的一点，则AP·AB的取值范围是（  ）.

A.（-2，6）    B.（-6，2）

C.（-2，4）D.（-4，6）

2.已知点P在圆x2+y2=1上，点A的坐标为（-2，0），O为原点，则AO·AP的最大值为    .

设计意图  根据平面向量数量积的定义a·b=|a||b|cos θ，其几何意义为其中一个向量的长度乘以另一个向量在其方向上的投影.投影法是从投影入手体现数量积的几何意义的方法.通过设计两道小题的作业训练，主要是帮助学生加深对平面向量数量积定义的理解和直观能力的培养，有助于提升学生数学抽象与直观想象等核心素养.

图2第2组  基底法

3.如图2，在△ABC中，AB=BC，∠B=90°，AC=42，D为AC的中点，在平面ABC中，将线段AC绕点D旋转得到线段EF.设M为线段AB上的点，则ME·MF的最小值为    .

图3

4.如图3，在四边形ABCD中，M为AB的中点，且AB=2，MC=MD=CD=1.若点N在线段CD（端点除外）上运动，则NA·NB的取值范围是（  ）.

A.-14，0B.0，34

C.14，1D.-34，0

设计意图  若无法直接获取对应向量数量积的要素，如平面向量的模和夹角，此时考虑采用基底法.例如第3题中ME=MD+DE，MF=MD+DF，第4题中NA=NM+MA，NB=NM+MB，都是将“未知向量”分解成“基底”（或已知向量）表示，再利用向量的数量积运算即可求解.通过设计两道小题的作业训练，主要是帮助学生加深对平面向量数量积的理解以及提升平面向量线性运算能力，有助于提升学生逻辑推理与数学运算等核心素养.

第3组  坐标法

5.已知△ABC中，A=π3，AC=2，AB=5，点P为边AB上的动点，则PB·PC的最小值为    .

6.已知正六边形ABCDEF的边长为4，P为正六边形所在平面内一点，则PA·PC+PE的最小值为    .

设计意图  坐标法就是将几何图形放在适当的坐标系中，将平面向量坐标化，利用向量之间的坐标运算来解答.本组中两个小题都是建立恰当的平面直角坐标系，求得相关点的坐标，根据数量积的坐标表示，求得PB·PC和PA·（PC+PE）的表达式，然后通过配方后即可求解最值.通过设计两道小题的作业训练，主要是帮助学生加强平面向量数量积的坐标表示的能力，有助于提升学生逻辑推理与数学运算等核心素养.

4.2  提高性作业

第4组  数形结合法

7.等边△ABC的面积为93，且△ABC的内心为M，若平面内的点N满足MN=1，则NA·NB的最小值为    .

8.在直角△ABC中，AB⊥AC，AC=3，AB=1，平面ABC内动点P满足CP=1，则AP·BP的最小值为    .

设计意图  利用数形结合法解决平面向量数量积的最值问题，往往是要利用“数”与“形”的转化，通过具体几何图形的分析，寻找取得代数式最值时的几何位置，对学生的要求较高，难度较大.例如本组中第7题利用向量数量积的运算律有NA·NB=NM2+NM·（MA+MB）+MA·MB，根據已知求相关向量的模，结合位置关系确定其最小值.根据三角形面积公式求△ABC边长，再应用等面积法、正弦定理求内切圆、外接圆半径，并判断N的轨迹及相对三角形的位置，最后由NA·NB=（NM+MA）·（NM+MB），数形结合求最小值即可；第8题由数量积的定义和平面向量基本定理可得AP·BP=4+CP·（AC+BC），当CP与AC+BC共线反向时，CP·AC+BC取最小值，即可得出答案.通过设计两道小题的作业训练，主要是帮助学生提升数形结合的思维能力，有助于提升学生直观想象与逻辑推理等核心素养.

第5组  极化恒等式法

图4

9.如图4所示，正方形ABCD的边长为1，A，D分别在x轴，y轴的正半轴（含原点）上滑动，则OC·OB的最大值是    .

10.已知Rt△ABC的斜边AB的长度为4，设P是以C为圆心，1为半径的圆上的任意一点，则PA·PB的取值范围是（  ）.

A.-32，52B.-52，52

C.-3，5D.1-23，1+23

设计意图  本组中第9题通过取线段BC中点M，运用极化恒等式将OC·OB转化为OM的表达式，求OM的最大值即可；第10题通过取线段AB中点M，运用极化恒等式PA·PB=PM2-AM2=PM2-4，将求PA·PB的取值范围转化为求PM的取值范围，体现了“化动为定”的转化数学思想.通过设计两道小题的作业训练，主要是帮助学生提升转化与化归的思维能力，有助于提升学生逻辑推理和数学运算等核心素养.

4.3  拓展性作业（探究）

11.平面内一组基底｛OA，OB｝及任一向量OC，OC=λOA+μOB（λ，μ∈R），若点C在直线AB上或在平行于AB的直线上，则λ+μ=k（定值），其中k为相似比，反之也成立.我们把直线AB以及与直线AB平行的直线称为“等和线”，基底OA，OB终点的连线AB称为“基线”.

图5

请运用“等和线”这一概念，探究完成下面问题：

（1）当“等和线”恰为直线AB时，k=    ；

（2）当“等和线”在O点和直线AB之间时，k∈    ；

（3）当直线AB在O点与“等和线”之间时，k∈    ；

（4）当“等和线”过O点时，k=    ；

（5）若两“等和线”关于O点对称，则两k值关系是    ；（选择：相等、互为相反数）

（6）定值k的变化与O点到“等和线”的距离成    .（选择：正比、反比）

（7）请运用上述“等和线”的性质解决问题：在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上.若AP=λAB+μAD，则λ+μ的最大值为（  ）.

A.3    B.22    C.5    D.2

12.在△ABC中，点M是BC的中点，则AB·AC=AM2-14BC2=AM2-14BC2.请运用平面向量此性质解决下列问题：

图6

（1）如图6，在△ABC中，D是BC的中点，E，F是AD的两个三等分点，BA·CA=4，BF·CF=-1，则BE·CE的值是    .

（2）已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则PA·（PB+PC）的最小值是（  ）.

A.-2  B.-32  C.-43  D.-1

设计意图  极化恒等式在必修第二册教材中第26页例2的解题过程AB·AC=a·b=14（a+b）2-（a-b）2中已出现，且在解决向量问题时思路清晰快捷，是必要的拓展.通过设计两道小题的作业训练，主要是帮助学生提升自主探究的学习能力，有助于提升学生逻辑推理和数学运算等核心素养.

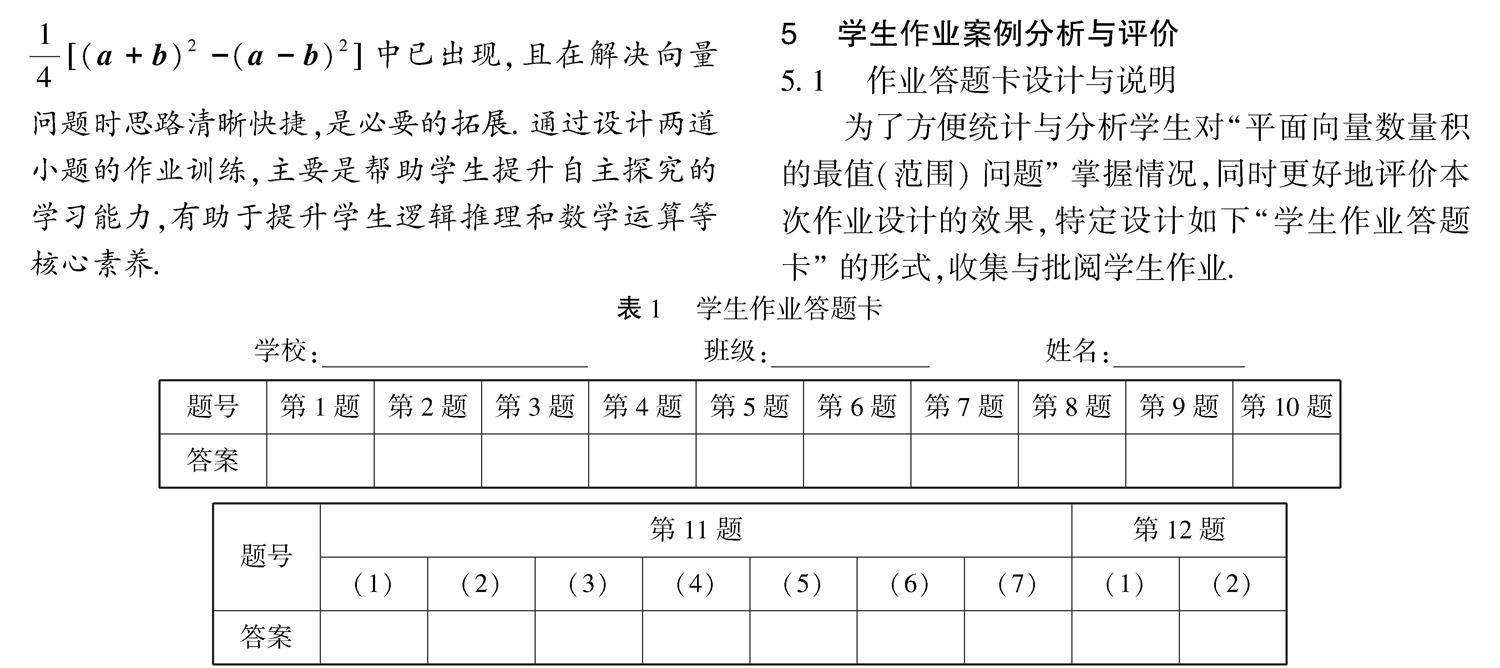
5  学生作业案例分析与评价

5.1  作业答题卡设计与说明

为了方便统计与分析学生对“平面向量数量积的最值（范围）问题”掌握情况，同时更好地评价本次作业设计的效果，特定设计如下“学生作业答题卡”的形式，收集与批阅学生作业.

情况说明  作业时间60分钟，作业总分70分，其中第1—10题每题5分，第11题和第12题每题10分，也可以不计分作业训练.

5.2  学生作业评价标准

对学生的知识和能力进行评价，有利于学生的查漏补缺和老师开展有针对性的教学.在对作业进行评价时，教师应当具体问题具体分析，在指出问题所在的同时多表扬学生的优点.

（1）学生是否能在预定的作业时长内完成本次作业：

50—60分钟：优秀；60—70分钟：良好；70—80分钟：一般.

（2）学生作业作答正确率是否合乎预期设计目标：

20%—40%：较差；40%—60%：一般；60%—80%：良好；80%—100%：优秀.

（3）学生学习能力的培养是否达到预期目标：（选择项后划“√”，只能单选）

基础性作业（较差□、一般□、良好□、优秀□），

提高性作业（较差□、一般□、良好□、优秀□），

拓展性作业（较差□、一般□、良好□、优秀□）.

（4）学生在知识与技能方面主要存在的薄弱环节：（选择项后划“√”，可以多选）

投影法□、基底法□、坐标法□、数形结合法□、极化恒等式法□、探究问题□.

5.3  学生作业具体分析

下面以我校高三（6）班（物理方向）和高三（15）班（历史方向）两个班级学生为例，分析作业答题情况，学生人数共计96人.下面分别从各个小题答题正确人数、不同题型答题正确率、不同类型作业答题正确率等三个方面统计分析学生答题情况.

图7  各小题答题正确人数统计

由图7统计分析可见，第1，4，11题设计比较简单；第2，3，5，6题难度适中；第7，8，9，10，12题较难.（此处统计仅供参考，因为统计可能存在偏差：选择题相对于填空题存在“猜中”成分多一点.同样图8、图9中统计也存在此种情况，下面不再赘述.）

由图8统计分析可见，学生对投影法、基底法和坐标法掌握较好；数形结合法、极化恒等式法和问题探究等方法掌握较差.

由图9统计分析可见，学生对基础性作业掌握较好，提高性作业和拓展性作业掌握一般.

6  作业设计反思与改进

作业设计与评价是为了检验教与学的成效.通过作业设计，诊断教与学过程中的优势与不足，通过作业评价，改进教与学的行为，促使学生数学学科核心素养的达成.

成功之处  （1）作业设计基本能达成本单元课时教学目标，较好地突出教学重点和突破难点；（2）作业设计思路清晰，层次分明，以“题型”为主线，同时兼顾“解法”为暗线；（3）作业设计较好地把握了平面向量数量积的最值（范围）问题中常考的题型及其解法，能起到复习巩固作用；（4）作业设计较好地显现出学生知识掌握程度，对投影法、基底法和坐标法掌握较好，数形结合法、极化恒等式法掌握有待提升.

改进之处  （1）作业题目整体难度偏大，难易梯度不明显，对学生素养要求较高，可结合学生实际降低作业题目难度；（2）作业设计有两处题型中涉及到极化恒等式法的训练题，可考虑优化合并；（3）“拓展性作业”中“探究问题1”设计问题过于细致，题目问题过多，可作“精减”，“探究问题2”中的探究揭示的“深度”不够，可作进一步探究过程的展现；（4）题目类型以“选择题”和“填空题”两种形式出现，相对于“解答题”不易较好地暴露出学生的问题；另外，选择题相当于填空题存在“猜中”成分多一点，统计分析可能存在偏差，可适当设计“解答题”；（5）由于有些作業题目存在一题多法，学生运用解法不一定是教师预设的方法，因此统计中显现出的学生对解法掌握情况存在偏差，只能仅供参考.

总之，教学与作业设计的完美契合，值得我们不断去探索和实践.作为一线的高中数学教师，应深入作业设计研究，把作业设计能力作为教师的基本功，在学习、实践、反思中设计出高质量的作业，让作业真正发挥其育人的功能［4］.

参考文献

［1］  张永超.基于核心素养落实的作业设计及其价值辨析［J］.中学数学教学，2022（01）：4-8.

［2］  沐方华，马晓骏.聚焦核心素养  寻绎作业样态：以高中数学作业设计与评价为例［J］.福建中学数学，2023（05）：26-28.

［3］  中华人民共和国教育部.普通高中数学课程标准：2017年版2020年修订［M］.北京：人民教育出版社，2020.

［4］  周宁，林新建.基于核心素养的高中数学课时作业设计实践：以“复数乘、除运算的三角表示及其几何意义”为例［J］.数学教学研究，2023，42（04）：20-23+67.

作者简介  杨瑞强（1979—），男，湖北黄冈人，中学高级教师，黄石市优秀班主任，黄石市优秀数学教师；主要从事中学数学教学与研究；发表文章100余篇.