一类涉圆锥曲线的两条直线交点坐标求解方法的研究

胡剑 李红庆

【摘要】回眸2022年北京、浙江及全国甲、乙卷4套高考数学试题的压轴题，研究者不难发现解析几何是排在首位的，也的确压准了中学数学教学中的轴线，并且深深地切入考生的痛点———数学运算策略、习惯与关键能力方法.通过纵向比较近5年高考解析几何趋势和横向剖析2022年全国4套试题及北京、浙江等试题，研究者就会发现压轴题其实都是涉圆锥曲线一条直线上点的坐标表示另一点的坐标的求解问题.顺着命题发展延伸脉络来观察，涉圆锥曲线的两条直线交点坐标求解问题会成为新的热点.鉴于此，文章将就命题生成机理分析、命题生成案例举隅、涉圆锥曲线两条直线交点坐标运算问题进行阐析.

【关键词】涉圆锥曲线；直线交点；坐标求解；关键能力；蝴蝶定理

引 言

通过纵向分析近5年高考解析几何命题趋势的走向，横向研究2022年高考试题中解析几何命题的共性，研究者发现2022年解析几何命题都是一类涉圆锥曲线一条直线上点的坐标表示另一点的坐标的求解问题.顺着解析几何命题发展趋势脉络来观察，涉圆锥曲线的两条直线交点坐标求解问题会成为新的热点，其本质是阿氏圆的相关元和蝴蝶定理的导向.

一、命题生成机理分析

这类问题是两条直线中每条直线中的线段都只有一个端点在圆锥曲线上，命题涉及的条件与结论都可能隐含着圆锥曲线某个重要的性质，多数都涉及阿波罗尼斯（Apollonius）圆（以下简称阿氏圆）的相关元的关系，蝴蝶定理和圆锥曲线的通性问题，先从高中数学需求方面简单地介绍阿氏圆.

（一）阿波罗尼斯（Apollonius）圆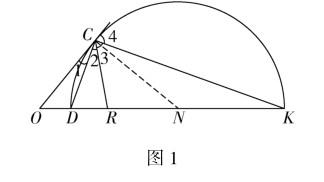

平面内动点C到两定点O，R的距离之比是不等于1的常数，那么动点C的轨迹就称为阿氏圆（如图1），其中阿氏圆N在直线OR上直径端点为D，K，并且点C是直线OC与阿氏圆N的切点，射线CD是∠OCR的平分线（∠1=∠2），射线CK是△OCR的外角平分线（∠3=∠4），由圆的切割线定理，得到重要结论OC2=OD·OK，这个结论往往体现在命题的结论中.

（二）阿波罗尼斯（Apollonius）圆的相关元

文[1]中曾介绍过蝴蝶定理在圆锥曲线与直线位置关系中的应用，其实它也是阿氏圆的性质的具体体现，现在介绍它的其他应用，并把这些性质统称阿氏圆的相关元的性质.

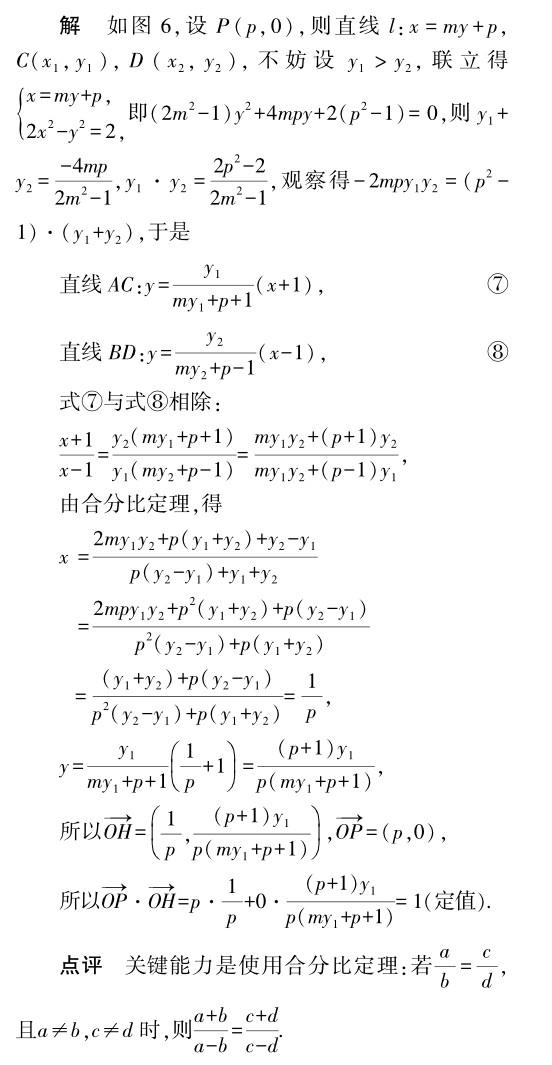
结 语

文章借助解决涉圆锥曲线的两条直线交点的问题，明确学生的关键能力是数学运算及利用同构式进行化简，从而灵活应用广义一元一次方程的多解條件解决定值、定点、定线问题.

【参考文献】

[1]骆银海，李红庆.解析几何中一类需要优先考虑用字母运算的问题及其解法[J].数学通讯，2023（1）：32-34，37.

[2]李红庆.跟我学解高中数学题（第2版）[M].哈尔滨：哈尔滨工业大学出版社，2021.

[3]李红庆.高考数学圈题典释（第2版）[M].北京：清华大学出版社，2013.