单向预制叠合板现浇层内力分布规律

岳琳琳 刘雪婷

摘要：采用有限元数值模拟及荷载试验分析，研究了普通钢筋混凝土单向预制叠合板现浇层支座弯矩的分布特征，对比了叠合板现浇层不同方向的支座负弯矩钢筋应变随加载过程的变化趋势，并分析了其形成机理。通过分析可知：加载过程中单向预制叠合板现浇层在顺预制板跨方向的支座负弯矩远大于另一方向，此规律与普通钢筋混凝土单向或双向板极限承载能力设计受力分析有一定差异。该结论对于在装配整体式结构设计中有效地控制叠合板现浇层开裂及优化设计有参考意义。

关键词：单向预制叠合板；现浇层；内力分布

中图分类号：TU375.2 文献标志码：A

0引言

由于施工便利的优势，采用下层预制上层现浇的叠合板，是当前钢筋混凝土在预制装配式建筑中主要采用的结构形式［1-2］。由于上、下层叠合面的抗剪能力是影响叠合板抗弯强度及刚度的关键，因此，近二十年来，很多研究都着力于分析不同形式的叠合面抗剪性能对叠合板整体抗弯强度和刚度的影响。聂建国等比较了不同形式的叠合面。

对简支叠合板承载能力的影响［3］。丁永君等［4］通过叠合板三维非线性数值模拟与试验对比分析了叠合板上、下层结合面受力特征。侯建国等［5］分析了结合面粗糙度对叠合板承载能力的影响。卫军和荆建梅等［6-7］研究了对叠合面拉毛处理的普通连续叠合板内力重分布特征。 值得一提的是，出于施工便利的原因，通过预制板单向布置，叠合板双向现浇形成的单向预制叠合板（或称“部分双向叠合板”）在实际工程中得到了大量运用［8-10］。吴方伯和聂磊等［11-12］研究了叠合面在理想结合条件下，单向预制叠合板弯矩分布规律及配筋计算方法。上述研究表明：经一般拉毛处理的叠合面抗剪切能力足够，叠合板正截面抗弯承载能力和尺寸相等的普通钢筋混凝土现浇板相近；单向预制叠合板可以按单向板设计，如果考虑现浇层的双向受弯，则设计计算方法比普通现浇双向板复杂很多［13］。

出于当前住宅产业化对叠合板的大量需求，施工简单的普通拉毛处理叠合面也得到广泛采用，也正因为有大量的应用需求，需要在设计上简便合理、安全可靠，希望能把单向预制叠合板当作普通钢筋混凝土单向或双向板进行受力分析，但事实上，由于单向预制叠合板与普通钢筋混凝土板在构造上的固有差异，特别是顺预制板跨度方向的叠合板边缘仅在现浇层部分有框架梁支座约束，导致在加载过程中现浇层支座钢筋受力情况较为特殊，如果处理不当，可能影响单向预制叠合板的正常使用［14-16］。因此有必要从加载全过程了解叠合板现浇层支座负弯矩变化机理，以确保单向预制叠合板正常使用极限状态符合相关规范要求。本文将通过数值模拟和足尺试验研究对上述问题加以分析，为普通钢筋混凝土叠合板的设计提供参考依据。

1数值模拟

1.1分析条件

由于本文侧重于分析叠合板达到极限承载能力前的内力分布规律，因此在塑性发展深度较小的近弹性阶段，叠合层与现浇层协调工作机理及内力分布是本文分析的重点。

1.2模型介绍

考虑一个4 m×4 m的梁格，四块长4 m，宽1 m，厚50 mm的预制板间隔平行摆放，间隔3 mm间距以确保预制板之间完全分离，现浇层板厚50 mm。由于板跨和板厚的比值远大于10，采用基于Kirchhoff的薄壳单元模型模拟预制板和现浇层在平面内和平面外可能的变形，预制和现浇层上下间距为实际两板抗弯横截面的中和轴距离。板弹性模量按C30混凝土确定，基于文献［4、7、8］都验证了普通拉毛处理叠合面良好的抗剪切能力，使得叠合板正截面承载能力能够等同于等厚度普通现浇板，因此在预制板和现浇层板单元上下之间，用剪切和弯曲刚度无限大的刚性短杆连接。为满足混凝土叠合板受力后变形的协调性，刚性短杆应均匀分布且其间距不宜过大。通过改变刚性短杆间距试验，发现当刚性短杆的间距小于等于500 mm时，叠合板在受力后现浇层的边界负弯矩不随着刚性短杆间距的减小而改变。在4 kN/m2荷载作用下SAP2000壳模型中叠合板现浇层顶面的应力云图可以和ANYSY实体模型很好吻合，因此在论文中刚性短杆的间距选500 mm。SAP2000模型如图1所示，受力后叠合板现浇层顶面应力云图如图2所示。

1.3边界条件

预制板和现浇层与框架梁的连接约束条件有所不同，预制板直接搁置于框架梁上，可作为铰支连接；现浇层与框架梁整浇，配置了充分数量的支座钢筋，可看做与梁单元固接。有限元建模时，通过在板和梁单元之间设立铰接或固接支座单元实现，如图3和图5所示，叠合板俩边框架梁剖面如图4和图6所示。

1.4分析结果

在叠合板表面加载4 kN/m2的均布荷载后，现浇板的负弯矩分布如图7所示。由于篇幅所限，对每个节点弯矩无法一一给出，且平行于各框架梁方向的负弯矩沿梁全长分布较均匀，在预制板拼缝处有一定变化。为了克服这种轻微突变带来的影响，将框架梁沿全长均分为三段，取各自区段内所有节点弯矩的均值，以反映现浇板支座负弯矩（表1）。弯矩矢量方向规定：以Y轴代表顺预制板跨度方向，以X轴代表与之垂直的另一个方向。

从表1可以看到现浇板支座负弯矩有几点分布规律：

（1）Y方向的现浇板支座负弯矩，在框架梁中部大于框架梁兩端。

（2）Y方向的支座负弯矩总体上大于X方向，在框架梁中部差异更为明显。上述现象是由于Y方向的框架梁没有对预制板起支撑作用，预制板在跨中部位挠度较大，因而现浇层在此处变形较大，容易产生较大的负弯矩值。而X方向的框架梁对预制板有支撑作用，预制板在X梁边缘附近挠度较小，现浇层在此处变形小，因此负弯矩较小。

2试验分析

2.1试件设计及测点布置

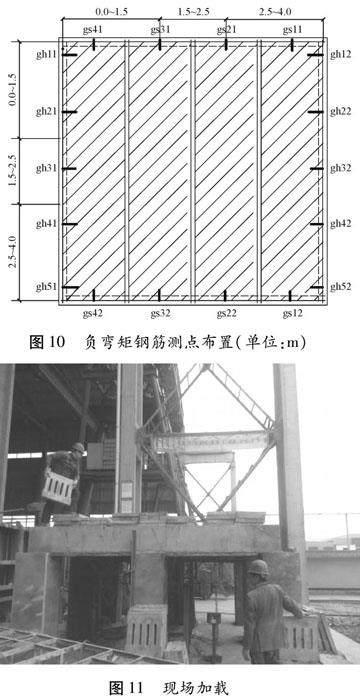
按上述模型尺寸进行足尺模型试验，混凝土等级为C30，预制板和现浇层配筋分别如图8和图9所示，预制板与框架梁之间有连接构造钢筋C8@200 mm，预制板横向拼缝处也有C8@200 mm构造钢筋。制作过程中，先施工预制板部分，并按设计要求做好叠合面的构造措施，然后在室内覆盖麻袋浇水养护10天。10天后接着浇筑现浇层混凝土，并用同样的方法养护7天。在混凝土叠合板制作过程中，板始终具有可靠支撑，避免加载前的二次受力。按GB/T50152-2012《混凝土结构试验方法标准》的相关规定，在现浇板上进行均布荷载的逐级加载，满载荷载为4 N/m2。试验过程中，对现浇板两方向支座负弯矩钢筋的应变进行了应变数据采集测量。负弯矩钢筋的测点如图10所示，现场加载如图11所示。

2.2试验结果分析

受自重其它施工荷载因素的影响，在施加均布荷载之前，现浇层负筋已存在拉应变，荷载逐级增加后，钢筋应变随之增加。通过图12和图13反映的两个方向的现浇板钢筋应变增加情况看，越接近承载能力极限，钢筋应变增加的趋势减缓。总体上看，越靠近现浇层边缘中部，钢筋应变越大。

图14反映了现浇层相互垂直的两个板边不同位置的负弯矩钢筋应变比值情况。gh31和gh51分别是顺预制板跨方向的现浇层边缘中部和端部测点，gs32和gs42分别是垂直于预制板跨方向的现浇层边缘中部和端部测点。50%加载时，gh31/gs32值约等于2.5，gh51/gs42的值约为1。50%持荷时，gh31/gs32和gh51/gs42的值变化很大，分别变为1和0.3。在加载70%之后随着均布荷载等级的增加gh31/gs32和gh51/gs42的值趋于稳定，最终在100%持荷阶段gh31/gs32=1.4，gh51/gs42=1，如图14所示。总体上看，相互垂直的两个板边缘的钢筋应变，中部差异大于端部差异。越接近承载能力极限，差异越小。

3结论

根据长宽比为1∶1普通钢筋混凝土单向预制叠合板的数值模拟和试验分析，在叠合板整体逐步达到承载能力极限状态的过程中，单向预制叠合板的现浇层有几点受力特征：

（1）相比垂直于预制板跨度的方向，顺预制板跨度方向的框架梁对叠合板现浇层的约束反力较大，对应的支座负弯矩钢筋应变也更大。

（2）叠合板现浇层相互垂直的两个边，其中部负弯矩钢筋应变差异较端部更大。

（3）上述差异随着荷载接近叠合板的承载能力极限而逐渐减弱。

综上所述，本文研究对于了解单向预制叠合板的受力机理，并为进一步优化单向预制叠合板设计提供了一定的参考。

参考文献

［1］孙哲哲，李明，赵唯坚.国内钢筋混凝土叠合板的研究进展［C］//第21届全国结构工程学术会议论文集Ⅲ.沈阳，2012：Ⅲ102-Ⅲ105.

［2］ 聂琳.混凝土叠合板在高层住宅中的应用［J］.建筑结构，2013，43（supⅠ）：541-544.

［3］ 聂建国，陈必磊，陈戈，等.钢筋混凝土叠合板的试验研究［J］.工业建筑，2003，33（12）43-46.

［4］丁永君，杜剑，吴学辉.叠合板拼缝搭接试验研究［C］//第七届全国现代结构工程学术会议论文集.杭州：2007，1730-1734.

［5］侯建国，贺采旭.预应力混凝土叠合板的叠合面受力性能研究［J］.武汉水利电力大学学报.1993， 26（3）：308-316.

［6］卫军，荆建梅，聂建国， 等.连续钢筋混凝土叠合板性能的研究［J］.郑州工学院学报，1990，11（2）：55-60.

［7］荆建梅，卫军，郭乐工.普通钢筋混凝土连续叠合板的性能［J］.工程力学，1997（supⅠ）：382-385.

［8］ 赵晓龙，林碧懂，刘丰峰.住宅工业化技术在万科第五寓的应用［J］.住宅产业.2011，5（8）：45-49.

［9］WILLIAMSON N. Concrete floors［M］. Butterworth-Heinemann， 2003：3-38.

［10］GHAVAMI K. Bamboo as reinforcement in structural concrete elements［J］. Cement and Concrete Composites，2005.27（6）：637-649.

［11］吳方伯，黄海林，陈伟，等.预制带肋底板混凝土双向叠合板实用弹性计算方法［J］.建筑结构，2012，42（4）： 100-103.

［12］聂磊，袁建伟，黄赛超.混凝土叠合双向板的内力和配筋计算［J］.长沙交通学院学报，1998， 14（3）：79-83.

［13］吴方伯，黄海林，陈伟，等.预制带肋薄板混凝土叠合板件受力性能试验研究［J］.土木建筑与环境工程，2011，33（4）：7-12.

［14］BIDDAH A. Structural reinforcement of bridge decks using pultruded GFRP grating［J］. Composite Structures，2006，74（1）：80-88.

［15］HASSAN A， KAWAKAMI M. Steel-free composite slabs made of reactive powder materials and fiber-reinforced concrete［J］. ACI Structural Journal，2005，102（5）：709-718.

［16］ROBERTS-WOLLMANN C L， GUIROLA M， EASTERLINA W S. Strength and performance of fiber-reinforced concrete composite slabs［ J ］ . Journal of Structural Engineering， 2004， 130（3）： 520-528.

［作者简介］岳琳琳（1997—），女，硕士，研究方向为工程结构。