基于Stacking集成学习的机械钻速预测方法

高云伟 罗利民 薛凤龙 刘洋 严昊 郑双进

基金項目：中国石油化工股份有限公司石油工程技术研究院科研项目“基于机器学习的机械钻速预测与施工参数优化方法研究”（35800000-22-ZC0607-0033）。

高云伟，罗利民，薛凤龙，等.基于Stacking集成学习的机械钻速预测方法17-24，52

Gao Yunwei，Luo Limin，Xue Fenglong，et al.ROP prediction method based on stacking ensemble learning17-24，52

机械钻速是评估石油天然气钻井作业效率的重要指标。为准确预测新疆工区某油田钻井机械钻速，基于该工区的历史钻井数据，利用局部离群因子检测算法对数据进行预处理，建立了基于Stacking集成学习的机械钻速预测模型，该模型通过Stacking集成策略融合K近邻算法（KNN）、支持向量机算法（SVM）和随机森林算法（RF）进行预测验证。预测验证结果显示，分类准确度不高。运用遗传算法进行各基础模型参数优化。优化后，基于KNN、SVM、RF及Stacking集成4种算法，预测机械钻速准确率分别为73.7%、78.9%、81.6%及97.4%，其中Stacking集成模型预测准确率最高。基于Stacking集成学习的机械钻速预测方法开发了机械钻速预测软件，运用软件预测其他2套施工参数下的机械钻速，结果表明，预测机械钻速与实际机械钻速一致，且性能稳定，表明该模型拥有较强的泛化性和较高的预测精度。该智能算法可为新疆工区的该油田机械钻速预测与钻井施工参数优化提供一种新手段。

机械钻速；预测模型；Stacking集成学习；机器学习；施工参数优化；预测验证

TE242

A

003

ROP Prediction Method Based on Stacking Ensemble Learning

Gao Yunwei1  Luo Limin1  Xue Fenglong1  Liu Yang2  Yan Hao3  Zheng Shuangjin3

（1.Shale gas Exploitation Technology Services Company，Sinopec Jianghan Oilfield Service Corporation;2.PetroChina Southwest Oil & Gas Field Company;3.School of Petroleum Engineering，Yangtze University）

Rate of penetration （ROP） is an important indicator to evaluate the petroleum drilling performance.To accurately predict the ROP at an oilfield in the Xinjiang work area，the historical drilling data from the area were processed using the local outlier factor （LOF） algorithm，and an ROP prediction model based on Stacking ensemble learning was established.The model integrated by Stacking strategy with the K-nearest neighbor （KNN），support vector machine （SVM） or random forest （RF） algorithm showed inaccurate classification in the verification.The genetic algorithm was then adopted to optimize the parameters of the basic models.The optimized models integrating KNN，SVM，RF and Stacking algorithms yielded the prediction results with accuracy of 73.7%，78.9%，81.6%，and 97.4%，respectively.Clearly，the Stacking-based model gets the highest accuracy.Thus，a software was developed using the Stacking-based model.It was applied to predict the ROP under two sets of parameters.The results show that the predicted ROP matches well with the actual ROP，and the software works stable.This proves the generalization and accuracy of the Stacking-based model.This intelligent algorithm has provided a new means to predict ROP and optimize drilling parameters at the oilfield of Xinjing work area.

ROP； prediction model;Stacking ensemble learning;machine learning;parameter optimization;forecast verification

0  引  言

高云伟，等：基于Stacking集成学习的机械钻速预测方法

机械钻速（Rate of Penetration，ROP）是评价钻井作业效率的重要技术指标，预测机械钻速可为钻井决策与施工参数优化提供依据，从而达到降本增效的目的。针对机械钻速预测的研究，国内外学者主要基于传统方法建立方程和机器学习2种方法来进行。在基于传统方法建立方程预测机械钻速方面，A.BAHARI等［1］建立了W.C.MAURER方程，但考虑因素不够全面；B.ADEBAYO等［2］建立了岩石特性、物理性质与机械钻速之间的经验公式，但未考虑钻井参数对机械钻速的影响；李昌盛［3］基于多元回归方法改进了B-Y钻速方程，使得不同地层的系数得以改变，但该方程只适用于钻井液钻井；S.KUMAR等［4］研究得到了较为准确的机械钻速预测模型，但模型参数受岩性影响较大，较为复杂；N.VAN HUNG等［5］总结出了针对旋转冲击钻头的机械钻速预测模型，但模型主要适用于高硬度地层，适用性不够广泛。在运用机器学习预测机械钻速方面，景宁等［6］运用层次分析法和前馈神经网络建立了机械钻速预测模型；王文等［7］、刘胜娃等［8］基于神经网络算法建立了机械钻速预测模型；C.HEGDE等［9］利用机器学习算法初步建立了机械钻速预测模型，并使用随机搜索法、粒子群算法、眼球法进行了优化完善；苏兴华等［10］利用K近邻算法、支持向量机等4种机器学习算法建立了机械钻速预测模型。

综上分析发现，目前机械钻速预测主要依靠经验，或在前人已建立的方程上进行改进，或是依靠控制变量等方法进行试验，以寻找影响机械钻速的主控因素。在机器学习算法预测机械钻速方面，目前大多使用单一模型，泛化性较差，难以完全满足当前钻井施工需求。为此，本文建立了一种基于Stacking集成策略融合K近邻算法、支持向量机算法和随机森林算法的机械钻速预测模型，并利用遗传算法对各基础模型进行参数优化。然后运用新疆工区某油田的历史钻井数据进行预测准确性验证，以期为该油田机械钻速预测与钻井施工参数优化提供一种新手段。

1  Stacking基础模型算法

1.1  K近邻算法

K近邻算法［11-13］ （K-Nearest Neighbor，KNN）是一种半监督类机器学习算法，具有十分成熟的理论基础和良好的使用稳定性。该算法的核心是首先测量新样本和训练数据集中已分类样本之间的距离，再按照与新样本最接近的K个邻居的多数类别来对其分类。常用的距离计算方法有欧式距离、曼哈顿距离和余弦相似度。其中，n维空间中点A（a1，a2，…，an）和点B（b1，b2，…，bn）之间的欧式距离do、曼哈頓距离dm和余弦相似度cos β计算方法为：

do=（a1-b1）2+（a2-b2）2+…+（an-bn）2（1）

dm=a1-b1+a2-b2+…+an-bn（2）

cos β=A·BAB（3）

式中：an为A点n维坐标；bn为B点的n维坐标；A为A点的属性向量;B为B点的属性向量。

K近邻算法基本流程如下：①利用历史数据集建立一个容量较大的且具有一定代表性的数据库；②设置状态向量；③计算出新状态向量和历史数据状态向量之间的距离；④确定近邻个数K的取值；⑤确定近邻权重；⑥通过对K个近邻进行加权，从而得到该算法的预测值。

图1为K近邻算法示例图。如图1所示，“？”代表未知类别的样本，“三角形”、“圆形”标记为已知类别的样本。图1设定KNN算法的K为5，那

么该簇内需要包含5个已知类别的样本，然后进行投票确定“？”所属的类别。很明显，图1中“三角形”类别的数量大于“圆形”类别的数量，可以确定这个“？”为“三角形”类别。

1.2  支持向量机算法

支持向量机算法［14-16］（Support Vector Machine，SVM）的主要思想是结构风险最小化原则和统计学习理论中的VC维理论。SVM算法在解决小样本、非线性回归模型中表现出许多特有的优势，在很大程度上克服了“维数灾难”和“过学习”等问题，可用于离散因变量的分类和连续因变量的预测。

该算法的原理如图2所示。图2中三角形标记为类别1，圆点标记为类别2，在虚线上的标记为“支持向量”。SVM利用核函数［17］将线性不可分问题转化为线性可分问题；若遇线性不可分问题，则需利用非线性变换。变换后划分超平面的方程为：

fx=ωTφx+b（4）

式中：ω为法向量；b为位移项；φ（x）为x的映射变换。

为使找到的超平面到不同类别之间的距离和最大，则需满足：

minω，b12ω2

s.t.yiωTφx+b≥1  i=1，2，…，m（5）

利用二次规划技术，并进一步引入核函数得到如下超平面方程：

fx=∑mi=1αiyikx，xi+b（6）

式中：αi为权重系数; yi为真实值;k为核函数;kx，xi表示x·xi；x为关于x的映射变换。

1.3  随机森林算法

随机森林［18-20］（Random Forest，RF）是集成学习算法之一，该算法组合了多棵决策树。本文所选用的为CART决策树，构建过程是假设训练集有N个样本，每个样本含有P个自变量和1个因变量。利用Bootstrap抽样法，从训练集中有放回的抽取出N个样本构建单个CART决策树；然后从P个自变量里面选择n个来作为建立决策树的自变量；再根据基尼指数生长出一棵未剪枝的CART决策树。最后构建多棵决策树，形成随机森林。其算法原理如图3所示。

由图3可见，该算法的核心思想是采用多棵决策树的投票机制，完成分类和预测问题的解决。对于回归预测问题，将多棵树的回归结果进行平均得到最终结果；对于分类问题，将多棵树的判断结果进行投票，以少数服从多数得到最终的分类结果。

1.4  Stacking集成算法

Stacking集成算法［21-25］属于集成学习中结合策略内的一种算法。该算法需要多个学习器支撑其训练过程，这些学习器分为初级学习器和元学习器，前者训练个体数据，后者训练集合数据。作为一种集成学习技术，Staking算法将来自多个预测模型的信息进行整合而形成新的模型，不同的算法用级联的组合形式进行组合。与单一的预测模型相比，Stacking集成学习具有更优的性能。本文使用K近邻算法、支持向量机算法和随机森林算法作为Stacking集成学习中的初级学习器。Stacking算法的具体运行原理如图4所示。

由图4可知，新的训练数据为基于初级模型训练得出。如果直接使用原始训练数据去训练元模型会产生过拟合，因此需要利用K折交叉验证法，用初级模型未使用的样本来产生后续建立元模型所需要的训练数据。以5 折交叉验证为例，具体过程如下：首先将样本划分为训练集和测试集；然后对单个初级模型，将训练集随机地平均分成5 份，每次使用其中的4 份数据去预测剩下的1 份数据。重复5 次后，将得到5 组预测结果，将这5 组预测结果合并，即为训练集的预测结果集合，这个预测结果集合即为次级分类器的训练集。同时，每一次预测时，也将测试数据进行预测，并将预测结果平均，作为次级分类器的测试集。最后将各个初级模型的结果组合起来，通过元模型进一步学习得到最终预测结果。

该训练过程的特点是，Stacking算法集合了第一阶段中各个初级模型通过训练得到的特征，吸收了不同模型在分类预测中的优点，得到的分类效果对比单一分类模型都要好。同时通过K折交叉验证方法，有效避免模型出现过拟合，进而提升由 Stacking 集成学习得到的组合模型的泛化能力。

基于上述过程，利用基于Stacking集成学习预测机械钻速的主要步骤如下。①对钻井区块的原始数据进行清洗和归一化处理，再将归一化处理后的数据集划分为训练集和测试集。②将训练集划分为K份，对各个初级学习器采用K折交叉验证法进行交叉验证；每次进行交叉验证时均用1份作为模型的验证集，剩下的（K-1）份作为模型的训练集。每次进行交叉验证结束后，利用经过训练后的学习器对测试集和验证集进行预测。③将单个初级学习器进行K次交叉验证后得到的每个验证集的预测值整合为矩阵M，将测试集的K份预测值按行平均得到矩阵Q。④第一部分初级学习器训练完成后可得到训练集输出特征矩阵（M1，M2，…，Mn），将此矩阵作为第二部分训练元学习器的训练集。⑤第二部分训练元学习器完成训练后，将矩阵（Q1，Q2，…，Qn）作为测试集，最终输出模型的预测值。

Stacking集成学习作为一种模型融合算法，在很多实际问题应用中能够取得相较于单一算法或者其他简单集成学习算法更优的表现，尤其在分类问题的处理上更是优势明显。目前该算法已广泛应用于分类、识别、预测等问题中［22］。

2  模型建立

2.1  数据预处理

这里所使用的建模数据均来自于新疆工区某油田钻井施工原始测井数据。数据共400组。原始数据包含牙齿磨损量、钻压、转速、钻井液排量、密度、漏斗黏度、钻头压降、钻头直径、机械钻速等特征。由于现场传感器老化以及人工操作等问题，原始数据库中部分数据存在噪声或异常，需要剔除这部分数据。

这里采用了局部离群点检测算法（Local Outlier Factor，LOF）进行数据预处理。该算法是一种基于密度的无监督高精度离群点检测方法，与传统的基于统计方法的离群点检测算法不同，局部离群因子检测算法不需要数据集服从特定的概率分布。此外，该算法还可以通过控制异常程度的阈值来控制离群点的数量。

局部离群点检测算法最核心的方法是关于数据点密度的计算，其原理如下：

（1）计算点p到o的距离d（p，o）以及点p的第k距离dk（p）=d（p，o），满足在数据集中至少有不包括p在内的k个点o′，有d（p，o′）≤d（p，o）成立；在数据集中最多有不包括p在内的k-1个点o′，有d（p，o′）＜d（p，o）成立。

（2）计算第k距离邻域。该计算方法与K近邻算法的邻域计算类似，定义Nk（p）为点p的第k距离邻域，满足：

Nk（p）=o′∈Cx≠p｜d（p，o′）＜dk（p）（7）

（3）计算可达距离，即点o到点p的第k可达距离见式（7），其至少是点p的第k距离：

Lk（p，o）=maxL（o），d（p，o）（8）

式中：Lk（p，o）表示點o到点p的第k可达距离；L（o）表示点p的第k距离；d（p，o）表示点p到点o的距离。

（4）计算局部可达密度，即点p的局部离群因子见式（8），表示点p的第k邻域内点到p的可达距离的倒数：

ρk（p）=Nk（p）∑o∈Nk（p）Lk（p，o）（9）

式中：ρk（p）为点p的局部可达密度；Nk（p）为点p的第k距离邻域。

（5）计算局部离群因子，即点p的局部离群因子计算见式（9）。如果Fk（p）接近于1，说明p与近邻点的密度相差不大，p与邻域内点属同一类型；若Fk（p）小于1说明p的密度比其邻域密度高，则p为密集点；若Fk（p）大于1说明p密度比邻域密度低，则p为异常点。Fk（p）计算式为：

Fk（p）=∑o∈Nk（p）ρk（o）ρk（p）Nk（p）（10）

式中：Fk（p）为点p的局部离群因子；ρk（o）为点o的局部可达密度。

局部离群点检测算法通过计算每个数据点的K近邻，并得到该点的局部离群因子，通过设定阈值，筛选出局部离群因子大于阈值的点，判定这些点为离群点。

利用Python中的Sklearn工具实现局部离群点检测算法，去除了原始数据中20组离群数据。为避免原始数据集的量纲和高维度影响预测结果，将处理后的380组原始数据使用标准化方法中的max-min方法进行处理。max-min方法为：

x′i=xi-xminxmax-xmin（11）

式中：x′i为归一化后的数据；xi为归一化前的原始样本数据；xmin为原始样本数据特征值的最小值；xmax为原始样本数据特征值的最大值。

2.2  机械钻速分级

通过分析该油田的机械钻速数据，由于钻头尺寸不同，机械钻速之间差异较大。根据现场经验将不同尺寸钻头的机械钻速分为3个等级：低钻速、中钻速和高钻速。钻速分级令机械钻速的数值大小不受钻头尺寸制约，且将建模任务从回归问题转化为分类问题，在提高模型预测精度的同时还有利于现场人员了解钻进状态。该油田机械钻速分级标准如表1所示。

2.3  建立預测模型

为避免该预测模型出现泛化能力不足的问题，并保证预测结果的准确性和稳定性，将预处理后的380组数据按照9∶1的比例随机划分为训练集和测试集，其中342个训练样本用于构建模型，38个测试样本用于评价模型。

利用Python中的Sklearn工具实现K近邻算法、支持向量机算法和随机森林算法，利用自编程序实现Stacking算法。以样本数据中的钻头入井新度、钻头出井新度、牙齿磨损量、钻压、转速、钻井液排量、密度、漏斗黏度、钻头压降、钻头直径为输入量，以机械钻速级别为输出量，基于K近邻算法、SVM算法、随机森林算法和Stacking算法建立默认参数的机械钻速预测模型。各模型的默认参数如下：KNN近邻样本数K为5，近邻样本投票权重相同，距离标准采用欧式距离；SVM的惩罚系数C取1，核函数g取0.1，核函数采用高斯核函数；随机森林算法设置决策树数量为200，叶节点最小样本量为1，不限制树的最大深度。构建Stacking集成学习模型整体分为2个阶段：首先，利用Stacking算法训练数据集训练初级学习器（初级模型）；然后，基于初级学习器生成新的训练数据集训练元学习器（元模型）。其中，K近邻算法、SVM算法、随机森林算法作为初级学习器，CART决策树算法作为元学习器，不对决策树最大深度做限制，叶节点最小样本量为1，根、中间节点能分割的最小样本量为2。

考虑该问题属于分类问题，采用准确率作为模型分类准确度的评价方法，具体思路为：分类准确度=分类准确组数/预测总组数。该次预测总组数为定值38组，默认模型预测结果如表2～表5所示。其中“低钻速为1，中钻速为2，高钻速为3”。表6为K近邻模型、SVM模型、随机森模型、Stacking集成学习模型预测机械钻速准确率的结果。

由表2～表6可见：KNN、SVM、随机森林、Stacking集成模型预测机械钻速的分类准确度均不高；虽然Stacking集成模型的分类预测准确度最高，但仍然只有81.6%。因此，需要对各算法参数进行优化，以提高模型的分类预测精度。

2.4  优化模型参数

遗传算法［26-28］（Genetic Algorithm，GA）是一种基于自然界遗传机制和生物进化论的高效随机搜索和优化的方法。此种算法是在求解过程中模拟生物界的进化机制，通过染色体的选择、交叉、变异操作，进而求取最优解。其核心是通过适应度函数评估个体的优劣，对于优势个体，在下一代种群中占据更高的占比。遗传算法相较于传统优化算法具有很强的鲁棒性。除此之外，全局搜索特性和隐含并行性也是其2大优势。

遗传算法优化步骤如下：①确定输入、输出变量，通过编码（本文采取二进制编码）将最优解问题转化为种群繁衍问题；②随机产生个体，设置种群；③确定适应度函数；④进行选择、交叉、变异操作；⑤计算适应度值并进行淘汰；⑥满足迭代停止条件则得到最优解，否则继续进行步骤④～⑥的操作。

对遗传算法的参数进行设置，具体如下：种群数量为150，繁衍最大代数为70，染色体长度为100，交叉概率为0.85，变异概率为0.01，适应度函数选用绝对误差。优化后的KNN近邻样本数K为30，近邻样本投票权重与距离成反比，距离标准采用曼哈顿距离；优化后的SVM惩罚系数为12，采用高斯核函数，核函数参数为0.1；优化后的RF的决策树数量为500，决策树最大深度为7，叶节点最小样本数为2。

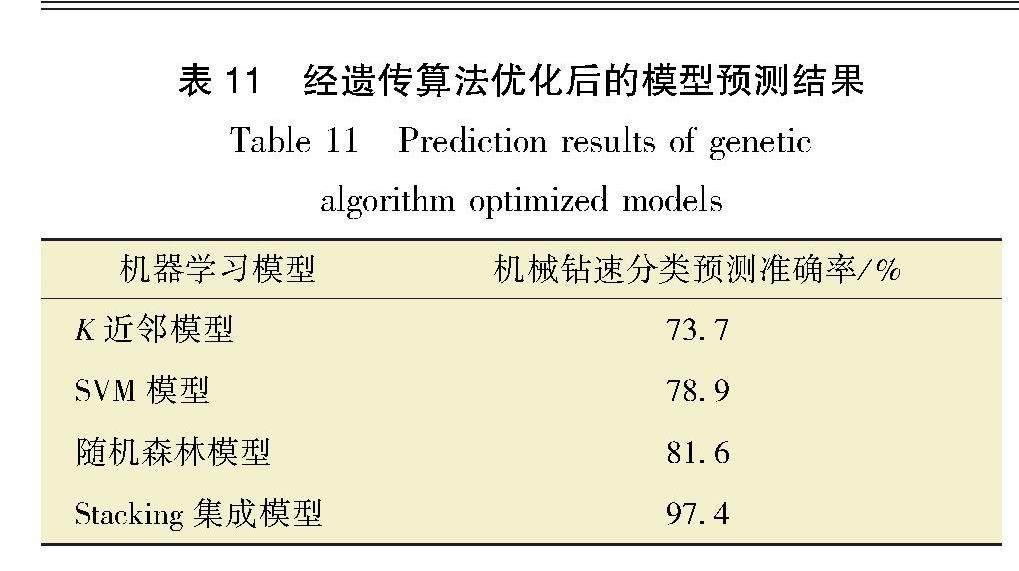
将优化后的模型参数输入对应模型，将全部优化后的参数利用Stacking集成算法进行融合，利用38组测试数据验证优化后模型的精度和泛化性，各优化后模型预测结果如表7～表11所示。

由表7～表11可知，经遗传算法优化后各模型的准确率均得到了提升，其中Stacking集成学习模型的分类预测准确率可达97.4%。由此可认为Stacking集成学习模型最适合于预测新疆油田机械钻速，为该油田机械钻速预测与钻井施工参数优化提供了一种新方法。如若其他区块或油田需要应用该方法预测机械钻速，可根据2.2节中方法，对该区块的历史施工数据进行提取和预处理后，再根据本区块经验对机械钻速进行分级，以此获取建立该区块Stacking机械钻速分级预测模型所需的原始数据。同时可以直接利用1.4节的思路构建Stacking模型，或利用当前泛化性和预测精度高的算法替换Stacking模型中的初级学习器或元学习器，以此获得更好的Stacking模型。

3  现场验证

基于遗传算法优化后的Stacking集成学习模型编写机械钻速预测软件，输入新疆工区某油田深井段施工参数：钻头入井新度100%，钻头出井新度50%，钻头牙齿磨损量50%，钻压80 kN，转速30 r/min，钻头压降0.53 MPa，钻头直径215.9 mm，钻井液密度1.6 g/cm3，钻井液循环排量24 L/s，钻井液漏斗黏度57s。

软件计算结果：该施工参数下机械钻速等级预测为“1-低转速，钻速小于4 m/h”，同理可得另外2套施工参数下的机械钻速预测数据，所得如表12所示。

由表12可知，运用Stacking集成模型预测所得的该油田机械钻速与实际机械钻速一致，表明该模型具有较强的泛化性和预测精度，验证了基于Stacking集成学习的机械钻速预测方法可用于预测该油田机械钻速等级与范围。现场作业人员可基于预测结果调整施工参数，动态优化钻井施工方案，可以提高该油田机械钻速与钻井施工效益。

4  结  论

（1）基于KNN、SVM、RF、Stacking集成学习4种算法分别建立了机械钻速预测模型，针对新疆工区某油田的历史钻井数据进行预测，准确率分别为63.2%、73.7%、76.3%、81.6%，上述集成模型的分类准确度均不高，基础模型准确率需要进一步优化。

（2）利用遗传算法对各模型的参数进行优化后，基于KNN、SVM、RF、Stacking集成4种算法预测机械钻速准确率分别为73.7%、78.9%、81.6%、97.4%，相比優化前准确率均有所提升，其中Stacking集成模型预测准确率最高。

（3）基于遗传算法优化的Stacking集成学习模型编写了机械钻速预测软件，利用不属于原数据集的新数据验证模型精度。在3组全新数据预测中，新模型的分类结果全部准确，说明该模型具有较强的泛化性和准确度。该方法可用于新疆工区某油田机械钻速预测与钻井施工参数优化。

［1］

BAHARI A，SEYED A B.Trust-region approach to find constants of bourgoyne and young penetration rate model in khangiran iranian gas field［C］∥Latin American & Caribbean Petroleum Engineering Conference.Buenos Aires： SPE，2007： SPE 107520-MS.

［2］  ADEBAYO B，AKANDE J M.Textural properties of rock for penetration rate prediction［J］.Daffodil International University Journal of Science and Technology，2011，6（1）： 1-8.

［3］  李昌盛．基于多元回归分析的钻速预测方法研究［J］．科学技术与工程，2013，13（7）：1740-1744．

LI C S.Study of method for predict rate of penetration based of multiple regression analysis［J］.Science Technology and Engineering，2013，13（7）： 1740-1744.

［4］  KUMAR S，MURTHY V M S R.Experimental studies on drill penetration rate prediction in coal measure rocks through Cerchar hardness index tests［J］.Journal of Mines Metals and Fuels，2014，62（4）： 88-95.

［5］  VAN HUNG N，GERBAUD L，SOUCHAL R，et al.Penetration rate prediction for percussive drilling with rotary in very hard rock［J］.Vietnam Journal of Science and Technology，2016，54（1）： 133-149.

［6］  景宁，樊洪海，纪荣艺，等．基于数据挖掘技术的深井钻速预测方法研究［J］．石油机械，2012，40（7）：17-20．

JING N，FAN H H，JI R Y，et al.Data mining technology-based research on the prediction method of deepwell ROP［J］.China Petroleum Machinery，2012，40（7）： 17-20.

［7］  王文，刘小刚，窦蓬，等．基于神经网络的深层机械钻速预测方法［J］．石油钻采工艺，2018，40（增刊1）：121-124．

WANG W，LIU X G，DOU P，et al.A ROP prediction method based on neutral network for the deep layers［J］.Oil Drilling & Production Technology，2018，40（S1）： 121-124.

［8］  刘胜娃，孙俊明，高翔，等．基于人工神经网络的钻井机械钻速预测模型的分析与建立［J］．计算机科学，2019，46（增刊1）：605-608．

LIU S W，SUN J M，GAO X，et al.Analysis and establishment of drilling speed prediction model for drilling machinery based on artificial neural networks［J］.Computer Science，2019，46（S1）： 605-608.

［9］  HEGDE C，DAIGLE H，GRAY K E.Performance comparison of algorithms for real-time rate-of-penetration optimization in drilling using data-driven models［J］.SPE Journal，2018，23（5）： 1706-1722.

［10］  蘇兴华，孙俊明，高翔，等．基于GBDT算法的钻井机械钻速预测方法研究［J］．计算机应用与软件，2019，36（12）：87-92．

SU X H，SUN J M，GAO X，et al.Prediction method of drilling rate of penetration based on GBDT algorithm［J］.Computer Applications and Software，2019，36（12）： 87-92.

［11］  COVER T，HART P.Nearest neighbor pattern classification［J］.IEEE Transactions on Information Theory，1967，13（1）： 21-27.

［12］  张著英，黄玉龙，王翰虎．一个高效的KNN分类算法［J］．计算机科学，2008，35（3）：170-172．

ZHANG Z Y，HUANG Y L，WANG H H.A new KNN classification approach［J］.Computer Science，2008，35（3）： 170-172.

［13］  张宁，贾自艳，史忠植．使用KNN算法的文本分类［J］．计算机工程，2005，31（8）：171-172，185．

ZHANG N，JIA Z Y，SHI Z Z.Text categorization with KNN algorithm［J］.Computer Engineering，2005，31（8）： 171-172，185.

［14］  丁世飞，齐丙娟，谭红艳．支持向量机理论与算法研究综述［J］．电子科技大学学报，2011，40（1）：1-10．

DING S F，QI B J，TAN H Y.An overview on theory and algorithm of support vector machines［J］.Journal of University of Electronic Science and Technology of China，2011，40（1）： 1-10.

［15］  张学工．关于统计学习理论与支持向量机［J］．自动化学报，2000，26（1）：32-42．

ZHANG X G.Introduction to statistical learning theory and support vector machines［J］.Acta Automatica Sinica，2000，26（1）： 32-42.

［16］  祁亨年．支持向量机及其应用研究综述［J］．计算机工程，2004，30（10）：6-9．

QI H N.Support vector machines and application research overview［J］.Computer Engineering，2004，30（10）： 6-9.

［17］  奉国和．SVM分类核函数及参数选择比较［J］．计算机工程与应用，2011，47（3）：123-124，128．

FENG G H.Parameter optimizing for support vector machines classification［J］.Computer Engineering and Applications，2011，47（3）： 123-124，128.

［18］  HO T K.The random subspace method for constructing decision forests［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1998，20（8）： 832-844.

［19］  LOH W Y.Regression tress with unbiased variable selection and interaction detection［J］.Statistica Sinica，2002，12（2）： 361-386.

［20］  BREIMAN L.Random forests［J］.Machine Learning，2001，45（1）： 5-32.

［21］  李珩，朱靖波，姚天顺．基于Stacking算法的组合分类器及其应用于中文组块分析［J］．计算机研究与发展，2005，42（5）：844-848．

LI H，ZHU J B，YAO T S.Combined multiple classifiers based on a stacking algorithm and their application to Chinese text chunking［J］.Journal of Computer Research and Development，2005，42（5）： 844-848.

［22］  徐慧丽．Stacking算法的研究及改进［D］．广州：华南理工大学，2018．

XU H L.The study and improvement of stacking［D］.Guangzhou： South China University of Technology，2018.

［23］  周星，丁立新，万润泽，等．分类器集成算法研究［J］．武汉大学学报（理学版），2015，61（6）：503-508．

ZHOU X，DING L X，WAN R Z，et al.Research on classifier ensemble algorithms［J］.Journal of Wuhan University （Natural Science Edition），2015，61（6）： 503-508.

［24］  李寿山，黄居仁．基于Stacking组合分类方法的中文情感分类研究［J］．中文信息学报，2010，24（5）：56-61．

LI S S，HUANG J R.Chinese sentiment classification based on Stacking combination method［J］.Journal of Chinese Information Processing，2010，24（5）： 56-61.

［25］  鞏俊芬．基于优化融合Stacking算法的贷款决策模型研究［D］．临汾：山西师范大学，2019．

GONG J F.The study of loan-decision model based on optimized and fusion stacking algorithm［D］.Linfen： Shanxi Normal University，2019.

［26］  HOLLAND J H.Adaptation in natural and artificial systems［M］.Ann Arbor： University of Michigan Press，1975： 390-401.

［27］  边霞，米良．遗传算法理论及其应用研究进展［J］．计算机应用研究，2010，27（7）：2425-2429，2434．

BIAN X，MI L.Development on genetic algorithm theory and its applications［J］.Application Research of Computers，2010，27（7）： 2425-2429，2434.

［28］  吉根林．遗传算法研究综述［J］．计算机应用与软件，2004，21（2）：69-73．

JI G L.Survey on genetic algorithm［J］.Computer Applications and Software，2004，21（2）： 69-73.

第一高云伟，高级工程师，生于1984年，2016年毕业于长江大学石油与天然气工程专业，获硕士学位，现从事石油天然气钻井及测试技术的研究与管理工作。地址：（430074）湖北省武汉市。电话：（027）59805701。email：Gaoyunwei.osjh@sinopec.com。

通信作者：郑双进，email：Zhengshuangjin@yangtzeu.edu.cn。

2023-11-28

宋治国