有限实验数据下工程结构概率建模及随机响应分析

张瑞景, 戴鸿哲

(哈尔滨工业大学 土木工程学院,黑龙江 哈尔滨 150090)

在随机工程问题中,合理考虑输入参数的随机性是获得可靠结构响应的关键[1-2]。随机输入在工程应用中普遍存在,如材料特性、外部荷载、结构系统的初始和边界条件等[3-4]。工程结构的随机参数往往具有明显的时空变异性和非高斯性,如岩土工程中的土壤参数和地下水高度、结构工程中的风荷载和地震激励以及水文中的降水和蒸发量等。此时,结构参数应建模为非高斯随机场[5-6];另一方面,在实际应用中,由于传感器的存储能力有限或增加观测的成本过高等原因,往往只能获得不确定的输入参数有限的实验数据[7-10]。因此,从有限的实验数据中合理地建模非高斯输入参数,并进一步进行后续随机响应分析具有重要的工程价值。近年来,为了解决实验数据下工程结构概率建模及随机响应求解的问题,学者们发展了各类方法。其中,最具潜力的是基于多项式混沌(polynomial chaos, PC)展开的方法。此类方法的基本思想是首先对非高斯结构参数进行Karhunen-Loeve(KL)展开,然后再将得到的KL随机系数进行PC展开。获得结构参数的PC模型后,即可利用基于PC的响应求解技术进行结构随机响应的求解[11-12]。

虽然有诸多优势,但基于PC展开的方法目前仍存在许多挑战。此类方法的第1个挑战为随机建模。具体来说,要想获得合理的输入参数模型,必须准确建模多维KL随机系数的非线性相关,并估计其联合概率密度。此外,构造从KL随机系数到PC变量的多维非线性变换还涉及到大量的高维积分。为此,有学者把KL随机系数假设为相互独立,从而大大简化了随机建模[13-14]。为了考虑KL随机系数的非线性相关性,Ghanem等[15-16]利用极大熵分布、直方图估计器来估计KL随机系数的联合概率密度函数,随后再使用Rosenblatt变换构建KL随机系数的Hermite PC表示。Soize[17]使用核密度估计器(kernel density estimation, KDE)估计KL随机系数的联合概率密度函数,然后通过蒙特卡罗积分求解KL随机系数PC展开的系数。使用KDE的优势在于其可避免其他密度估计器在高维密度估计中的维数灾难[18]。

除随机建模外,PC类方法的另一挑战则为后续随机响应分析的求解效率。众所周知,对于服从Wiener-Askey族分布的随机输入而言,使用Wiener-Askey PC可实现结构响应的最优收敛[19]。然而,在实验数据有限的情况下,KL随机系数的分布通常在Wiener-Askey族之外,继续采用Wiener-Askey PC会导致结构响应分析的效率降低;另一方面,即使已构造出能使响应最优收敛的PC展开,由于PC变量存在复杂的相关性,后续的结构响应分析仍具挑战[20-21]。不难看出,要想使PC类方法可应用于实际工程结构分析中,关键为以下2方面:首先,要能够从实验数据中精确地建立基于PC的结构参数模型;其次,后续响应传播的效率应当足够高,以适应处理高维和大规模问题的工程需求。

本文开发了一种实验数据下的PC类结构随机分析方法。提出了一种KDE来估计KL随机系数的联合分布,从而得到结构参数的随机模型。进一步构造了KL随机系数的任意多项式混沌(aPC)展开,并利用一种基于D-optimal的加权插值法来求解结构的随机响应。

1 实验数据下非高斯结构参数的随机模型

实验数据下的随机结构分析第1步是合理建模非高斯结构输入参数。基于KDE的随机场建模方法,提出了一种可准确描述结构参数非高斯行为的随机场模型。

1.1 有限实验数据下非高斯结构参数的KL展开

令w(xi,θ),i=1,2,…,M为随机场w(x,θ)在M个位置xi处的一条实验数据,则N条独立的实验数据构成了随机场w(x,θ)的实验数据集W。其中,W={w(xi,θj)},i=1,2,…,M,j=1,2,…,N。随机场W(θ)={w(xi,θ)}的m阶截断KL展开可表示为:

(1)

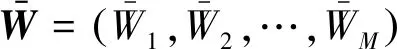
(2)

式中U为所有元素均为1的N维列向量。

KL随机系数ξi(θ)则是由其实验数据表征,即:

(3)

i=1,2,…,m;j=1,2,…,N

其中Wj=[w(x1,θj),w(x2,θj),…,w(xM,θj)]。

(4)

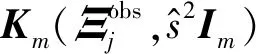
1.2 基于改进KDE的随机模型

为了从实验数据中准确地建模非高斯结构参数,本文提出了一种用于KL随机系数联合分布估计的新型KDE。该新型KDE的优点为得到的随机场模型准确可重构非高斯参数的最关注的2个概率特征,即二阶相关性和边缘分布。由于随机场W(θ)的边缘分布实质上是由一维KL随机系数的线性组合而得到的,因此,为了匹配结构输入参数的边缘分布,式(4)中的带宽s应根据一维KDE的选取准则来确定。一维KL随机系数的概率密度为:

(5)

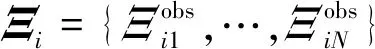
(6)

式中wi是带宽s(i)的权重。wi的值随i的增加而减小,即i越小的带宽s(i)对ssh的贡献越大,与特征值更大的KL随机系数对随机场边缘分布贡献更大这一现象契合。确定带宽ssh后,KL随机系数ξ(θ)联合密度变为:

(7)

一旦KL随机系数的联合分布通过式(7)确定,输入参数的非高斯模型即可由式(1)确定。

1.2.1 新型随机场模型的统计性质

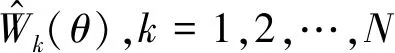
(8)

(9)

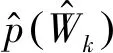
(10)

由式(10)可得,本文随机模型的二阶相关性为:

(11)

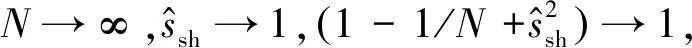
2 结构响应分析的任意多项式混沌法

尽管PC类的方法可以求解结构的随机响应,由于在实验数据下传统的Wiener-Askey PC可能会导致较低的计算效率,PC类方法在实际工程结构随机分析中的应用仍存在较大局限[22]。本文结合了结构响应分析的PC类方法,然后将KL随机系数的联合分布选为aPC的权函数,从而导出了结构输入参数的aPC表示。随后,进一步发展了基于aPC展开的高效随机响应分析方法。

2.1 基于多项式混沌的结构随机响应分析

在基于PC的结构随机分析中,结构响应通常与结构随机参数投影到相同的PC子空间中。结构参数随机模型中KL随机系数ξ(θ)的PC展开为:

(12)

式中:η(θ)为m维的PC变量;P=(m+p)!/(m!p!)为PC展开的截断项数,p为m维标准正交多项式Ψj(·)的阶数;αij则是PC系数。将式(12)代入式(1),即可得到非高斯输入场的PC展开为:

(13)

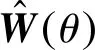
(14)

式(14)也可写为Y(η)≃αTΨ(η)。

2.2 任意多项式混沌展开的构造

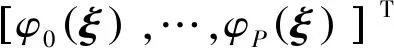
E[φi(ξ)φj(ξ)]

(15)

构造Ψ(ξ)的关键在于求解式(14)中的多维积分。一般地,该积分应使用蒙特卡罗积分进行近似:

(16)

式中Ξ(k)为KL随机系数ξ(θ)的第k个样本。虽然样本Ξ(k)可通过MCMC方法产生,其中涉及的数以万计次的联合概率密度计算导致抽样效率低。此外,MCMC样本之间存在的自相关性会大大降低蒙特卡罗积分的精度。为了高效高精度地构造矩阵G,本文使用了文献[24]中提出的KL随机系数的高效抽样方法。式(7)可写为:

(17)

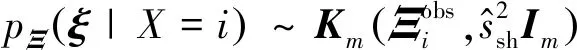
2.3 基于aPC展开的结构随机响应分析

aPC展开构造完毕后,需开发求解结构随机响应的算法。众所周知,基于aPC的结构响应分析关键在于求解式(14)中的aPC系数αk。大体而言,求解系数αk的方法大体可分为侵入式和非侵入式2类,由于非侵入式方法中的插值法可直接调用第三方软件进行结构分析[25],因此本文的研究主要围绕插值法来开展。插值法的精度和鲁棒性很大程度上取决于配置点的选择(即实验设计)。目前,独立PC变量的实验设计方案已日趋完善,而相关PC变量的实验设计方案还鲜有报道。基于aPC的响应分析的关键在于抽取aPC变量的蒙特卡罗样本。一旦获得aPC变量的样本,就可直接开发出aPC变量的实验设计方案,并进行后续的响应求解。

注意到aPC变量本质上是KL随机系数,而KL随机系数服从混合高斯分布,故aPC变量的独立样本可直接产生。因此,各种独立PC变量下的实验设计方案即可直接推广至aPC变量的实验设计。为实现结构响应的高精度估计,本文提出了一种D-optimal加权插值方法。首先,本文将估计式(14)中aPC系数的问题列式为加权插值形式:

(18)

根据D-optimal理论,ΞED可通过求解优化问题确定:

(19)

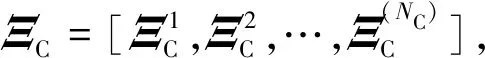
(20)

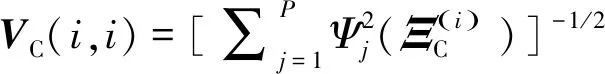
ΞED=ΞC(πED,:)

(21)

其中,πED=π(1:NED)。一旦确定了配置点ΞED,结构响应的aPC系数即可通过式(18)估计。

2.4 有限实验数据下工程结构随机分析方法

本文提出的实验数据下的新型结构随机分析方法总结如下:

1)对非高斯结构参数的实验数据进行KL展开,得到均值向量,截断后的特征值、特征向量及KL随机系数ξ(θ)的样本实现;

3)产生KL变量的独立样本,构造aPC基函数;

4)再次产生KL变量(aPC变量)的样本实现,随后利用选列主元的QR分解确定用于加权插值法的D-optimal配置点。通过式(18)估计随机响应的aPC系数并利用式(14)求解结构的随机响应。

步骤1)、2)旨在构建实验数据下结构输入参数的新型随机模型。为高效确定后续的随机响应,步骤3)将模型中的KL随机系数进一步用aPC展开。最后,步骤4)开发了有限数据下基于aPC的随机响应分析方法,从而形成了有限数据下工程结构的随机建模和后续响应传播的统一框架。注意到,由于步骤2)中的新型随机场模型考虑了输入参数分布与KL随机系数分布之间的内在关系,因此本文的随机模型可以准确地重构结构参数的边缘分布和二阶相关性,从而有效地构建了结构输入参数的非高斯特征。此外,本文发展了结构响应求解的D-optimal加权插值法,实现了结构随机响应的高效高精度求解。由于本文方法可对结构输入参数进行合理地随机建模,并进行高效的结构响应分机分析提供了一个有效的框架。

3 工程算例

在实际工程中,工程结构的不确定参数往往分为2大类:1)工程结构自身的机械和几何特性。例如,由于成分和制造工艺的原因,复合材料的杨氏模量通常表现出空间变异性。在实际工程中,人们不可能完全地确定杨氏模量的概率信息,只能得到一组从有限数目的试件中识别出的杨氏模量的实验数据;2)工程结构参数不确定性则源于外荷载。例如,地震动是一种具有强烈时空变异性的自然灾害,在特定的场地条件下,记录到的真实地震动时程往往十分有限。本文通过非线性结构在有限地震动数据下的随机分析的来说明所发展方法的应用。有限的加速度时程记录从太平洋地震工程研究中心建立的NGA强震数据库中根据如下特定场地标准选择出来:地震震级5≤M≤6,震源距离1 km≤D≤20 km,中硬土,土层的剪切波速Vs≥600 m/s。满足此准则的地震动记录共102条,将处理后的18 s的时程离散为1 801个点,步长Δt=0.01 s,如图1所示。为保留95%以上的总能量,此算例截断项数取为50。

图1 根据准则选出的102条地震动时程

方差是反映随机地震动统计特性的一个重要指标。为验证本文模型随机地震动的性能,图2给出了地震动时程的方差。由于随机地震动方差在整个时程中波动剧烈,对整个时程而言,地震动方差的值不在一个数量级,为便于观察,本文仅展示了0～8 s的结果。可以看出,传统KDE模型给出的边缘分布明显偏离了观测值,而本文建模方法给出的地震动时程的方差与观测值良好匹配。图3给出了t=1.5 s、t=6.5 s、t=11.5 s和t=16.5 s处地震动时程的观测边缘分布与模型边缘分布的Q-Q图,即Quantile-Quantile图。传统KDE模型给出的边缘分布明显偏离了观测到的边缘分布,无法捕捉到地震动的非高斯特征。相比之下,本文的随机模型给出的边缘分布与观测结果吻合良好,说明了本文建模方法的有效性。

图2 0～8 s地震动的方差

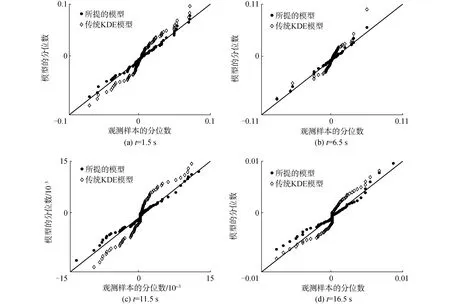
图3 4个典型时刻下地震动边缘分布的Q-Q图

为了验证所发展的结构随机响应分析方法的性能,本文进一步研究了20自由度滞回非线性结构在受随机地震动激励下的随机响应。其中,结构的质量和层间刚度参数如表1所示。

表1 20自由度非线性结构的质量和层间刚度

结构的非线性行为由Bouc-Wen滞回模型表征,其控制方程为:

(22)

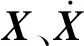
在本算例中,式(16)中用于构造aPC基函数的KL独立样本个数选取为K=105,D-optimal实验设计中候选样本容量取为NC=104。将所得系统响应与2×104次MCS给出的参考值进行比较,评估了所提响应分析方法的精度。分析结果显示,2阶aPC 展开即可对系统随机响应进行高精度近似。此时,只需对式(22)中的非线性滞回系统进行(50+2)!/(50!2!)=1 326次确定性评估。因此,本文方法可对受随机地震动激励的强非线性系统进行高效高精度的响应分析。为更直观说明本文方法的求解精度,部分随机响应分析的结果展示如下。图4和图5分别给出了1阶和2阶aPC展开所得的第2层随机位移响应的均值和方差及相应的绝对误差,而图6给出了第15层在t=1.5 s时的位移响应及相应的绝对误差。可以看出,由于结构的强非线性行为,采用1阶aPC展开并不能充分地近似结构响应。然而,当使用2阶aPC展开时,本文方法对系统随机响应的近似精度迅速上升,实现了系统响应的高精度预测。

图4 第2层位移响应的均值及均值的绝对误差

图6 t=1.5 s第15层位移响应的概率密度函数及绝对误差

4 结论

1)本文开发的随机模型考虑了结构参数分布与KL随机系数分布之间的内在关系,可准确地重构输入参数的边缘分布和二阶相关性,从而有效地捕捉结构参数的非高斯特征。

2)本文构造的输入参数任意多项式混沌表示配合所发展的D-optimal加权插值法可实现非线性系统随机响应的高效高精度评估,从而为有限实验数据下工程结构的随机分析提供了一个有效的框架。

3)算例验证了本文方法在随机维数为50维的问题中的有效性。但是,此方法在更高维度随机问题中的应用有待进一步研究。