时变指向约束下姿态参数空间离散化路径规划方法
2024-05-27朱哲徐瑞李朝玉朱圣英龙嘉腾朱雷
朱哲,徐瑞,李朝玉,朱圣英,龙嘉腾,朱雷
(1.北京理工大学深空探测技术研究所,北京 100081;2.深空自主导航与控制工信部重点实验室(北京理工大学),北京 100081;3.上海航天控制技术研究所,上海 201109)
0 引言
航天器在姿态机动时,其本体或可动部件的姿态受到指向约束,这类约束缩小了航天器姿态机动的可行域,被称作姿态指向约束。航天器姿态违反姿态指向约束时,会出现强光天体进入相机视场、天线偏离通信目标等问题,航天器的导航定姿、科学观测或通信传输能力将遭到损坏,影响任务正常执行。姿态指向约束包括禁忌指向约束和强制指向约束[1]。进一步地,随着深空探测任务的发展,航天器在姿态机动任务中可能同时面临多种姿态指向约束。例如在以OSIRIS-REx 为代表的小行星采样返回任务中,探测器在对自旋小行星进行附着抵近时,需要同时规避太阳强光干扰并对小行星地貌进行观测[2-4]。前者是传统静态禁忌指向约束;而后者在快速自旋小行星的条件下,对探测器提出了强制指向约束,且约束方向矢量在日心轨道惯性系下是动态变化的,形成的指向变化角不可忽视,构成了动态时变的强制指向约束。另外,探测器在行星探测任务中,惯性系下部分天体,例如行星的卫星,相对于探测器有较高动态的相对指向变化。当该天体具有高反射率时,例如卡西尼任务中探测器飞掠经过土卫二时,会对光学敏感器(如导航相机、星敏感器)等构成强光干扰[5-7],该类天体对探测器造成了时变禁忌指向约束。又例如,在类似罗塞塔号的彗星探测任务中,探测器在彗星抵近观测时受到彗尾和彗星气体喷流对敏感器和载荷视场的影响,需执行一定的姿态机动进行规避[8-9]。由于彗星相关地质活动具有不确定和动态特性,这类深空环境对探测器载荷指向轴构成了一类动态的禁忌指向约束。这类新型复杂任务场景使得深空探测器面临与以往任务不同的、随时间变化的姿态指向约束,该约束使姿态机动可行域成为一个动态空间,探测器需要在姿态参数的动态空间中满足姿态对准或跟踪的机动需求。而传统姿态路径规划大多只能使用静态空间的路径搜索算法[10-12]处理静态指向约束。时变指向约束带来的新问题对姿态路径规划方法的应用提出了挑战。
针对复杂多约束下航天器的姿态机动规划问题,姿态规划方法需要统一考虑指向约束和动力学约束等多种约束,综合求解得到姿态机动路径(姿态参数序列)和包括角速度和控制力矩序列在内的姿态机动轨迹。目前,求多约束下无目标优化航天器的姿态机动离散可行解主要采用包括势函数法、随机规划算法、空间离散化路径搜索算法在内的启发式约束评价规避算法。其中势函数法适合处理简单指向约束的情况[13]。随机规划方法能高效适应航天器的各种复杂约束情况,He等[14]使用RRTGoalBias 算法生成了时变指向约束下的姿态机动路径,并提出姿态随动球面来表示姿态机动和指向约束变化的动态过程。但其随机扩展过程生成的路径具有不确定性,路径不具有全局优化性。空间离散化路径搜索算法因具备较强的几何约束处理能力和较为完备的全局优化性能,在时变指向约束下的姿态规划问题中具有较高研究价值。
空间离散化路径搜索算法首先对姿态空间或姿态参数空间进行投影离散化,然后采用图搜索算法求解得到满足指向约束的姿态机动路径。图搜索算法以已知信息的姿态和约束空间为基础,通过构建图搜索寻找到达目标的机动路径。首先对姿态空间或者姿态参数空间进行投影离散网格划分,然后求解得到满足指向约束的姿态机动路径。常见的图搜索算法包括A*搜索算法,其最初由Hart等[15]发表。通过构造启发式函数,A*算法可以获得较好的寻的性能。Stentz[16]在此基础上提出D*和Focused D*算法,在处理动态插入障碍的地图路径搜索方面获得了较好效果。近年来图搜索算法被应用在姿态机动路径的规划问题求解上,Kjellberg等[17]通过二十面体方法将单位天球离散化为描述某个本体固联轴方向的像素图,而后利用A*搜索算法得到满足单轴禁忌约束的姿态机动路径。在此基础上,Kjellberg等[18]又进一步扩展算法的通用性,将二十面体方法应用于姿态四元数表示方式形成的超球面空间的离散化当中,实现了求解复杂多轴指向约束下的姿态机动路径。Tanygin[19]采用最小失真变换将完整的三轴姿态表示投影到一个三维空间,并将该投影空间在三维笛卡尔网格上离散化,而后利用图搜索算法得到满足复杂多轴约束的姿态机动路径。进一步地,Tanygin[20]又将该算法由求解单一目标点问题扩展到求解多个目标点构成的连续体问题。Calaon等[21]针对航天器敏感器对准导航天体和载荷规避强光天体的需求,将路径搜索算法应用于修正罗德里格斯参数的三维网格中,生成满足指向约束的离散参考路径,进而采用B-样条曲线拟合路径离散点,满足姿态运动学的同时能够优化控制力矩代价。进一步地,Calaon等[22]将拟合曲线扩展到非均匀有理B 样条曲线(NURBS),从而得到整体控制力矩代价更优的姿态轨迹。空间离散化路径搜索算法可以有效地处理多轴复杂指向约束,并通过启发式评价函数最小化从起点到终点的路径上所有节点的总路径代价。但该算法本身适用于几何类型约束,生成姿态路径离散节点,无法处理角速度和控制力矩有界约束以及姿态动力学约束,动力学类型的约束需要在路径拟合和轨迹规划算法中考虑。
为了使图搜索算法生成的路径满足动力学约束,引入轨迹规划算法生成含有角速度和控制力矩的完整姿态机动规划序列。以多项式方法[23-24]为例,采用一定阶数的多项式来表示航天器姿态机动过程中的姿态变化曲线,然后结合逆动力学方法[25]求解角速度和控制力矩。通过优化多项式系数,实现匹配边界条件。
本文提出了一种姿态参数空间离散化路径规划方法,通过姿态参数空间离散化、动态空间路径搜索、逆动力学轨迹规划3 部分实现完整的姿态机动规划。首先对基于修正罗德里格斯参数的空间离散化方法进行研究,实现姿态空间离散化的空间构建和指向约束表达。在此基础上,设计时变指向约束下的姿态路径搜索方法,设计非奇异空间搜索代价函数,通过引入节点时间特性处理时变指向约束,实现姿态路径生成。进一步采用多项式路径拟合,用逆动力学法计算姿态机动的角速度和控制力矩轨迹。最后数值仿真展示了不同组合的时变指向约束下,采用空间离散化方法规划的姿态机动路径的效果,验证了时变指向约束下路径规划的可行解。
1 姿态参数空间离散化
对于姿态参数空间离散化方法,需要针对不同的姿态描述方式,即姿态描述参数,选择不同的三维空间离散化方法,并实现姿态机动的指向约束表示。本节对修正罗德里格斯参数(MRP)描述方式进行了参数空间离散化处理,从而构建姿态空间的三维离散网格,结合离散空间的指向约束表达,得到姿态机动的路径规划空间,为空间离散化路径搜索算法设计提供了基础。
1.1 姿态描述参数
航天器姿态采用本体坐标系与惯性坐标系之间的相对转动关系来描述,刚体航天器姿态可以采用四元数和修正罗德里格斯参数进行描述。
1)四元数
采用单位四元数描述航天器的姿态:
式中:ev表示沿欧拉轴的特征向量;ϕ表示欧拉旋转角,ϕ∈[0,180°]。由于‖q‖=1(‖ · ‖表示欧几里得范数),四元数的4 个参数中只有3 个独立,四元数空间事实上是一个四维超球面。
2)修正罗德里格斯参数
修正罗德里格斯参数(MRP)用于表示SO(3)空间中的刚体旋转姿态,是三维向量表示的姿态参数,可由四元数导出:
式中:ϕ∈[0,360°)
相较于四元数空间,对MRP 参数空间进行离散化处理好处在于,MRP的3个参数相互独立,因此构成一个无限大的三维空间,R3内任意点均表示一个有效的三轴姿态指向(但一个三轴姿态并不唯一对应于R3内某一个点)。但与此同时,ϕ等于360°时MRP发生奇异,为了避免该奇异性,在MRP的“无限空间”中划出一定范围的集合,为后续路径搜索提供一个非奇异空间。
由于对MRP 表示的每个旋转σ=(ev,ϕ),存在一个对应的影集(Shadow set)σ'=(ev,ϕ'),ϕ'=ϕ-2π,表示相同的姿态[26]。对于单个σ对应的σ',下文称为节点σ对应的影节点σ'。对于σ'的分量:
式(3)成立时,2 组MRP 参数σ和σ'取值不同,是参数空间中不同的点,但表示相同的姿态,当‖σ‖>1时‖σ'‖<1。可以证明,对于MRP在表示一个360°旋转,即ϕ=360°时的奇异情况,有MRP 空间原点处σ0可表示同一姿态。
由此,选取限定区域的MRP 空间集合,MRP 空间以单位球为界,对于球外的一个节点所表示的姿态,存在球内某一个对应的节点所表示姿态与之相同。而对于单位球球面上的点,有‖σ‖=1,σ'=-σ,其中心对称的节点即其“影节点”。
由上述可以得到,所需离散化的MRP 参数空间可以限制在一个单位球内部及其球面,任意刚体航天器姿态可对应该集合内的一个三维MRP 坐标,该单位球及其球面构成了路径搜索的非奇异空间。
采用MRP 参数σ描述惯性系下的航天器姿态,在σ表示下的姿态运动学方程如下所示,方程说明了MRP 参数的时间导数与本体系下角速度ω的关系。
式中:σ2=‖σ‖2,[B(σ)]定义为:
式中:σ×是σ的斜对称叉乘矩阵。
1.2 修正罗德里格斯参数空间离散化
由于MRP 的参数空间不需经过投影、扭曲,其离散化节点通过三维笛卡尔网格划分即可实现均匀分布,相邻节点距离相等(其中单位球面上的离散节点取笛卡尔网格与球面的交点),路径搜索算法以离散化MRP 空间为工作空间。笛卡尔网格的离散化精细度可用笛卡尔坐标系一条半轴上单位球内等距排列的节点个数表示,例如单元格长度为1/a,离散化精细度N=a。
以精细度N=60 为例,离散化MRP 空间如图1所示。

图1 修正罗德里格斯参数空间笛卡尔网格划分效果及其剖面局部Fig.1 Cartesian grid of MRP space and its cross-section(part)
由立方体结构可知,对于距离单位球表面足够远的每个节点,其相邻节点共26个,分3 种相邻节点距离的取值‖ ‖σ=1 球面表面节点的邻近节点应包括其对应“影节点”σ'=-σ,如以为当前节点σi的相邻扩展节点,位于单位球的对侧,从而保证姿态机动在欧拉旋转角大于180°时的路径连续性。
1.3 指向约束在姿态参数空间的表示
姿态指向约束是一种几何约束,在参数空间的路径搜索中缩小了姿态机动路径的可行域,限定了规划路径的边界。因此,需要将指向约束也映射到参数空间中。姿态指向约束包括禁忌指向约束和强制指向约束,分别表示规避特定指向进入视场角的约束和“强制”姿态处于指向角范围内的约束。rgi表示光敏元件、载荷等设备在本体系下的视场中心(特征轴)方向矢量,rI表示约束关联天体在惯性系下的方向矢量,θj表示约束对应的视场角。本文考虑时变指向约束,当载荷目标天体相对于航天器本体运动,例如着陆器对自旋小行星的表面观测,rI随时间发生指向变化,约束视场角也可能时变。指向约束要求天体指向和设备特征轴的方向矢量夹角与视场角构成不等式约束,下式中符号“≤”表示禁忌约束:
式中:CIB,CBI是本体系与惯性系之间的方向余弦矩阵。
符号“≥”表示强制约束:
对于MRP 参数空间内的姿态指向约束表达问题,由于空间中任一节点需要同时满足全部约束,任意一个在禁忌指向约束之内,或强制指向约束之外的姿态对应的姿态参数节点都应从路径搜索的可行域中排除。值得注意的是,对于相邻两个可行域上的节点,其节点连接的转移路径事实上不一定在连续的每一处都满足约束,但由于姿态指向约束均为凸约束,该情况可通过设置适当的离散化精细度N避免。
以图例说明,对于安装在刚体探测器本体系z轴上的敏感器,视场角为20°,考虑两个方位角-仰角分别为[90°,-30°],[-90°,30°]和一个沿z轴正方向的禁入锥,其指向约束在惯性系单位天球和MRP参数空间的表示分别如图2、图3所示。

图2 惯性系下指向约束Fig.2 Pointing constraints in inertial frame

图3 修正罗德里格斯参数空间内的指向约束Fig.3 Pointing constraints in MRP space
类似地,对于两个方位角-仰角分别为[0°,0°]、[-180°,0°],视场角分别为20°的禁入锥,和方位角-仰角为[-180°,0°],视场角为20°的强制锥,其指向约束在惯性系单位天球和MRP 参数空间的表示分别如图4、图5所示:

图4 惯性系下指向约束Fig.4 Pointing constraints in inertial frame

图5 修正罗德里格斯参数空间内的指向约束Fig.5 Pointing constraints in MRP space

图6 静态约束下借助MRP影节点的连续路径Fig.6 Continuous path under static constraints by MRP switching
由此,在MRP 空间中,每个姿态指向约束构成了一块连通的几何区域,姿态对应的节点需要受到在该区域之内或之外的约束,即强制或禁忌指向约束。进而,时变指向约束是约束方向矢量rI在惯性系下动态变化的指向约束,时变指向约束在MRP 空间表示为随时间运动的一个连通区域,使得MRP 空间中路径搜索的可行域边界动态变化。
2 时变指向约束下姿态路径搜索方法
在姿态参数空间离散化和指向约束表达实现的基础上,姿态机动的路径规划问题已经转化为一个路径搜索问题。问题求解的目标是在离散化的MRP 空间内,从起点代表的初始姿态,到终点代表的目标姿态,找到一条能够满足时变指向约束的三维路径,时变指向约束由动态变化的几何障碍/可行域所代表。本文分析了以Focused D*为代表的路径搜索算法在MRP 空间中进行时变约束下路径规划的不足,从非奇异空间搜索和时变约束冲突定位两个方面进行改进,设计了非奇异空间时变约束路径搜索方法,得到满足时变约束的姿态机动执行路径,该路径由离散节点序列组成。
2.1 Focused D*路径搜索算法分析
由于D*和Focused D*分别是Dijkstra 和A*的反向搜索,Focused D*算法中当前节点σi的启发式评价函数包括两个部分。前序代价函数(h(σi))表示从终点到当前节点的路径代价,当当前节点与指向约束冲突时,代价函数将赋予较大的惩罚值。后序代价函数(g(σi))表示当前节点到起点的路径代价。每个节点的总路径代价f(σi)=g(σi)+h(σi)。
Focused D*算法中的主要函数包括:1)PROCESS_STATE(),用于寻找f(σi)最小的最优路径;2)MODIFY_COST(),用于路径与动态约束冲突时做节点代价修正,从而规划新的路径。
每个节点的总路径代价f(σi)=g(σi)+h(σi)。前序代价函数h(σi)等于前一节点h(σi-1)加上前一节点网格坐标grid(σi-1)到当前节点坐标grid(σi)的路径转移代价,一般采用欧几里得距离计算,σ0=σG为终点坐标。如果当前节点违反指向约束则惩罚值设为inf,节点扩展过程中动态维护节点的h(σi)和k值。
后序代价函数g(σi)由当前节点网格坐标grid(σi)到起点网格坐标grid(S)的欧几里得距离计算得到。
对于本文所解决的时变指向约束问题,Focused D*算法存在以下不足:
1)规划解在MRP空间无最优性
将Focused D*路径搜索算法应用于MRP 空间,应考虑到将搜索空间设定在MRP 单位球范围内时,该空间的非奇异性是由单位球外侧节点集的影集能映射到球内部来保证的,该搜索空间实际上无边界。因此应当存在这样的路径:从起点向球面外侧方向扩展,到达球面后,取在球面上的路径节点的影节点,通过相对于球心处于对侧位置的影节点回到球面内部,扩展到达目标位置。该路径是连续的。
原Focused D*算法以当前节点到目标节点的欧几里得距离为代价函数,生成解将排除所有上述穿越边界、对侧返回的路径(如图8所示),路径解失去了最优性。为实现非奇异空间搜索,路径代价计算时的欧几里得距离计算应与影节点到目标节点的距离做对比。
2)路径修正函数无法定位与时间相关的约束冲突节点
MODIFY_COST()的路径修正函数在原框架下是触发式的,即一旦将初始路径所含节点取代为障碍位置,便修正从被取代节点开始到目标节点的路径,生成新的路径。因此原方法无法估计时变指向约束在某一时刻与初始路径的冲突节点位置,进而无法定位路径修正的触发点,无法完成时变约束下的路径规划。
对于时变指向约束问题,在考虑时间特性的情况下,航天器执行的姿态机动在当前时刻的姿态对应了路径的当前节点σi,过去时刻的姿态对应路径上身后的节点σi-m,未来预期执行的姿态对应路径上身前的节点σi+n,n>1。如果因为指向约束的时变,由过去时刻姿态组成的已执行路径在当前时刻与约束发生冲突,或未来预期执行的路径在当前时刻与约束发生冲突,都不能被证明会影响航天器实时姿态机动的执行,因而无需修正现有路径。因此,在时变指向约束下的姿态路径规划当中,需要将节点放在时间线上,每个节点具有自身唯一对应的时刻,即航天器姿态机动至该状态的时刻。判断当前节点到下一节点的扩展是否与该时刻的指向约束冲突,冲突则调用MODIFY_COST()修正路径。值得注意的是,这一路径上的动态修正是预先规划的,建立在已知时变函数的动态约束条件上,而非执行过程中的实时修正。
根据上述不足,本文对时变指向约束下的路径搜索算法进行改进,提出了非奇异空间时变约束路径搜索算法。
2.2 非奇异空间时变约束路径搜索算法
在Focused D*算法应用中,路径代价函数是基于MRP 空间中节点间的欧几里得距离d(σ1,σ2)计算的。由于MRP 节点σ存在影节点σ',节点之间的距离计算应当选取grid(σi)和grid()到另一节点的欧氏距离的最小值,即:
如此则路径搜索算法可以在MRP 非奇异空间中向各个方向均等地扩展,确保规划出总代价函数最优的全局路径的合理性。前序代价函数h(σi)定义如下:
后序代价函数g(σi)定义如下:
当姿态机动欧拉旋转角大于180°时,借助MRP影节点的连续路径效果如下。
由式(9),在‖ ‖σ=1 的球面表面节点与其影节点σ'的距离=0。当路径扩展出单位球面,而通过影节点从球面的中心对称一侧进入时,=0,说明路径是连续的。
在时变指向约束条件下,离散化空间和指向约束构成的路径搜索空间需要随节点在初始规划路径上的运动动态更新。由路径搜索算法生成的含N+1 个节点{q0,q1,…,qN} 的姿态机动路径被分为N段,需对每一段路径的边界节点赋予时刻特性。由于姿态总机动时间T未知,对T的估计可以通过假设一个期望的平均机动角速度ωˉ,结合式(4)、(5)得到:
通过估计的总机动时间和期望平均角速度,可将路径上节点对应时刻{t0,t1,…,tN}设为与节点路径长度成比例关系的数值,即:
节点在路径上对应时刻的时变指向约束为{rI(ti),θk(ti) },i=0,…,N,k表示第k个指向约束的视场角。将时变指向约束引入路径搜索算法的动态环境更新中,可采取两种方式:
1)沿总路径代价最小的最优路径转动过程中算法存储的map 空间动态更新,这种方法需要在循环中重复离散化的空间构建,用时较长;
2)在节点遇到障碍的判断函数isCollision(X)中加入对时变指向约束的判断,需要将MRP 笛卡尔网格节点坐标转换为姿态参数,进而利用式(7)、(8)对指向约束特征轴方向矢量rgj(j个指向约束)进行判断。
采用两种方式的非奇异空间时变约束路径搜索算法结构中如图7所示:

图7 非奇异空间时变约束路径搜索算法流程图Fig.7 Flowchart of nonsingular time-variant path searching algorithm
3 逆动力学方法求解姿态连续轨迹
对于路径搜索生成的离散节点序列,需要采用插值拟合曲线将离散路径节点串起来,从而生成一条航天器能够跟踪执行的姿态机动轨迹。本节首先给出四元数表示下的姿态逆运动学和动力学方程。进一步地,由于路径搜索的MRP 节点序列可以简单地转换为四元数节点序列,对路径节点序列采用四元数多项式插值进行拟合。生成的四元数时间拟合曲线便可使用逆动力学方法计算角速度和控制力矩曲线,得到完整的姿态机动轨迹。
3.1 姿态逆运动学和逆动力学
刚体航天器本体坐标系下的姿态动力学方程为:
式中:J是惯量矩阵,ω=[ωx,ωy,ωz]T是角速度矢量,T是控制力矩。采用单位四元数q=描述惯性系下的航天器姿态,设Ω=[0,ωx,ωy,ωz]T,姿态运动学方程如下:
式中:运算符◦表示四元数乘法。
设q*是q的共轭四元数,逆运动学方程如下[25]:
对上式求微分得到:
式中:qI=[1,0,0,0]T。结合式(14)的动力学方程和式(17),可以得到用于计算控制力矩T的逆动力学方程:
式中:vec(·)表示四元数的向量部分。式(16)和(18)说明可以由q(t)推导ω(t)和T(t)。
3.2 基于四元数多项式插值的路径拟合
采用基于四元数多项式插值的逆动力学方法[27],生成满足离散路径点的姿态机动连续轨迹,包括姿态角速度和控制力矩。
对于路径搜索算法生成的含有N+1 个节点{σ0,σ1,…,σN}的姿态机动路径,使用式(2)的转换关系得到{q0,q1,…,qN} 的四元数路径。路径分为N段,在每段路径的时间[ti-1,ti]内,对四元数4 个分量的分别采用三次多项式插值,即分段三次样条插值,满足边界条件{q0,q1,…,qN} 。插值多项式如下:
总共有4N个三次插值多项式,有16N个多项式系数需求解。姿态机动路径节点和边界条件提供了等数量的约束方程。其中边界条件{q0,q1,…,qN}和初始及末端角速度为零提供了8N+8个约束方程:
式中:qi,j是qi第j个分量。
由分段多项式的分段连续条件,除去总路径的两个端点,中间N-1 个节点处角速度和角加速度,即的一阶和二阶导数相等,这提供了余下的8(N-1)个约束方程:
进一步地,姿态机动轨迹的四元数需要满足归一化条件,即‖q(t)‖=1。归一化插值函数表示为:
综上所述,通过计算多项式全部系数,可以得到q(t),,的分段数值表达式,角速度ω和控制力矩T可以由式(16)和(18)计算。
特殊地,当离散节点序列类似图8,通过MRP影节点保证路径连续到达目标节点时,难以直接进行插值拟合。可以先将节点序列映射为影节点序列,与原影节点分段相连接,构成连续路径。进而可以采用本节方法插值拟合生成解析轨迹,得到角速度和控制力矩时间曲线。

图8 姿态参数空间离散化方法在MRP空间的规划路径Fig.8 Path planned by attitude parameter space discretization path planning method in MRP space
4 数值仿真
为了验证所提出的姿态参数空间离散化路径规划方法的可行性,本节进行了数值仿真。考虑了深空探测器在外部动态指向约束下,从初始到目标姿态的重新定向姿态机动过程。首先,对多个时变禁忌指向约束下的姿态机动路径规划进行仿真,对比生成路径与传统方法结果的更优性。然后,同时考虑禁忌约束和时变强制约束,给出这一条件下的姿态规划结果。
4.1 动态禁忌指向约束下姿态规划
对姿态路径规划的参数空间离散化方法进行仿真,考虑深空探测器在本体系z轴方向上安装一个光学敏感器,其单位方向矢量用rB表示;需要在姿态机动过程中规避两个明亮天体,在惯性系下的单位方向矢量用rF1,rF2表示;要求rB与rF1,rF2之间的最小夹角为θF1,θF2;考虑指向约束的时变条件,对rF1,rF2有旋转角速度ωF1,ωF2。环绕器转动惯量为J,初始姿态为q0,目标姿态为qf;初始和目标角速度符合ω0,ωf符合双零约束。在路径规划和轨迹规划的参数定义方面,空间离散化的精细度定义为N,期望平均角速度为,δt是路径拟合时间步长。具体数值如表1所示。

表1 禁忌指向约束仿真条件Table 1 Simulation parameters under forbidden constraints
仿真环境为Matlab R2021b,计算机主频3.20 GHz,内存16 G。在时变指向约束下,采用基于MRP 空间离散化的姿态路径搜索算法,在表1 仿真条件下对问题求解。姿态参数空间离散化方法在MRP 空间的规划路径如图8 所示,算法在单位天球惯性系上的姿态指向路径如图9 所示,该路径是探测器在算法的规划结果不断修正过程中实际执行的节点路径。

图9 敏感器光轴在单位天球惯性系上的指向路径(图中所示为初始指向约束)Fig.9 Path of sensor axis on unit celestial sphere in inertial frame(initial pointing constraints displayed)
图8展示了MRP空间中成功规避两个禁忌约束的实际运动节点组成的机动路径。由于禁忌约束的方向矢量随时间在惯性系下摆动变化,图9 展示了与图8 对应的在单位天球惯性系下,敏感器指向实际执行的机动路径。该实际机动路径与每一次路径搜索算法规划的路径都不同,这是因为每当原先规划路径与该时刻时变指向约束冲突时,算法都对路径进行动态修正,生成从当前点到目标的新路径。
规划路径动态修正中的变化展示在图10中(选取了3次修正路径),三角形符号表示当前时刻姿态机动的敏感器指向,即路径上的当前姿态节点;指向约束随时间从图中左侧摆向右侧。从起点到终点的路径经过算法修正的次数实际上等于时变指向约束与当前节点沿先前路径扩展发生冲突的次数。通过多次路径修正,最终确定一条与图9所示相同的、探测器可实际执行规避时变约束的机动路径。
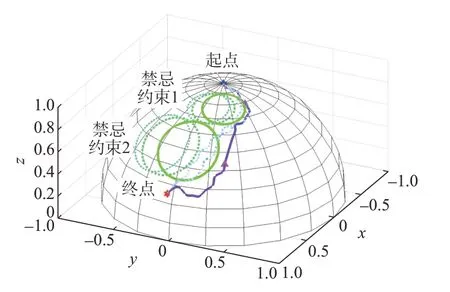
图10 单位天球惯性系上不同时刻下算法修正的三维指向路径(指向约束随时间在图中从左向右摆动)Fig.10 3D pointing path on unit sphere in inertial frame at different time(as time-variant pointing constraints swinging from left to right)
图11 给出了MRP 和单位四元数及角速度、控制力矩随时间的变化轨迹。MRP 和四元数之间可以相互转换,其时间曲线说明姿态机动过程无退绕。角速度时间曲线显示角速度的模在期望值ωˉ=0.03 rad/s 附近保持小幅波动。单轴控制力矩最大值不超过1 N · m。其中,控制力矩时间曲线在起始和末端的较大幅值对应角速度在起始和末端的加速和减速,从而满足角速度的双零约束。在40~50 s时间段控制力矩的快速增加造成了角速度分量的较大变化,角速度发生转向,对应了此时路径对于禁忌约束2的“应急”修正。

图11 MRP、单位四元数及角速度、控制力矩随时间的变化轨迹Fig.11 Trajectory of attitude(MRP and quaternion),rate and control torque over time
与文献[14]中时变指向约束下基于改进RRT的姿态规划方法进行对比,由于RRT 方法规划结果具有随机不确定性,取多次重复规划结果,将本文方法与其进行比较。在相同仿真条件下,将上述结果的规划路径长度与RRT 方法的40 次规划结果进行比较,如图12所示。

图12 空间离散化方法规划路径长度与RRT方法的40次重复仿真结果对比Fig.12 Path length comparison between space discretization method and RRT for 40 times
其中姿态机动路径的长度计算方式如下[18]:
式(24)计算得到两姿态节点对应姿态qm,qn之间的路径长度(rad)。由此可以计算整条四元数姿态路径的机动“路程长度”,即路径长度。图12 显示,本文的路径搜索算法基于Focused D*算法进行改进,规划路径的评价函数与路径长度相关,因此具有较好的路径长度优化效果,与文献[14]中RRT 方法的结果相比,路径长度大大缩短。图13直观展示了天球坐标系下本文方法与随机选取的文献[14]中RRT 方法生成的2 条路径的对比,RRT 方法结果因其随机不确定性,对约束的规避方向可能不同,路径的长度分布差异较大。

图13 敏感器光轴在单位天球惯性系上的指向路径(本文方法与RRT方法结果对比)Fig.13 Path of sensor axis on unit celestial sphere in inertial flame(results compared with RRT)
需要说明的是,图13反映了单位天球上的敏感器指向路径,该路径长度与式(24)计算的四元数路径长度不同:前者只能反映敏感器方向矢量在天球上划过的角度,后者则是探测器三轴姿态在三轴姿态机动中的路径长度度量。图13 中两条RRT 方法路径由式(24)计算,长度分别为5.085 6和7.140 8,作为对比,本文方法生成路径的长度为1.925 3.
4.2 动态强制指向约束下姿态规划
进一步地,考虑小行星探测器在附着过程中对自旋小行星进行定向观测的时变强制指向约束条件,定义附着相机安装在本体系z轴方向上。在姿态机动过程中同时规避2 个明亮天体,构成静态的禁忌约束,方向矢量为rF1,rF2,视场角设置与前一节相同。在惯性系下的强制约束方向矢量用rM1表示,要求rB与rM1之间的最小夹角为θM1,rM1有旋转角速度ωM1。对应ωM1的取值大小,设置期望平均角速度ωˉ。定义新的初始与目标姿态q0,qf,仿真条件设置如表2。

表2 加入强制指向约束的仿真条件Table 2 Simulation parameters introducing mandatory constraints
其中强制指向约束角速度ωM1参考小行星2016HO3自旋周期0.467 h,角速度大小设为0.2°/s,约等于0.003 5 rad/s.
在上述条件下,姿态参数空间离散化方法在MRP 空间和惯性系单位天球上,探测器实际机动路径如图14,15所示。由于强制约束要求三角形符号表示的当前姿态节点始终在图15 中浅蓝色强制约束范围内,当前节点到目标姿态节点σG的路径由于超出强制约束边界而无法规划,需要设置一个临时目标节点。将临时目标节点设为:位于当前时刻指向约束的可行域内,到目标姿态节点的距离(用式(9)计算)最小的节点,该节点在强制约束边界上。采用分段式规划,分别规划一条满足强制约束和禁忌约束的、从当前节点σi到临时目标节点的路径,和一条只需满足禁忌约束的、从临时目标节点σ'G到目标姿态节点σG的路径。两段路径相连接即从起始到目标姿态,且满足当前时刻强制约束和禁忌约束的机动路径。当前节点扩展与时变强制约束冲突时,如果≠σG,则选取新的临时目标节点,修正σi到的路径,并修正到σG的路径;如果=σG,直接修正σi到σG的路径。最终得到一条每一时刻姿态节点都满足时变强制指向约束的探测器可执行路径,即图14、15所示路径。

图15 单位天球惯性系上不同时刻下算法修正的三维指向路径(强制约束随时间在图中从上向下摆动)Fig.15 3D pointing path on unit sphere in inertial frame at different time(as time-variant mandatory constraints swinging from top to bottom)
MRP 和单位四元数及角速度、控制力矩随时间的变化轨迹如图16所示。角速度时间曲线显示,角速度的模在期望值ωˉ=0.004 rad/s附近保持小幅波动。单轴控制力矩最大值不超过0.02 N·m。由此可知,与前一节角速度期望值ωˉ=0.03 rad/s时单轴控制力矩最大值不超过1 N·m 相比,角速度期望值越大,控制力矩幅值的峰值越大,通过设置期望角速度可以使控制力矩满足姿态机动的有界约束。

图16 MRP、单位四元数及角速度、控制力矩随时间的变化轨迹Fig.16 Trajectory of attitude(MRP and quaternion),rate and control torque over time
将强制约束下的规划结果同样与RRT 方法进行对比,取多次重复规划结果。在相同仿真条件下,将上述结果的规划路径长度与RRT方法的40次规划结果进行比较,如图17所示。
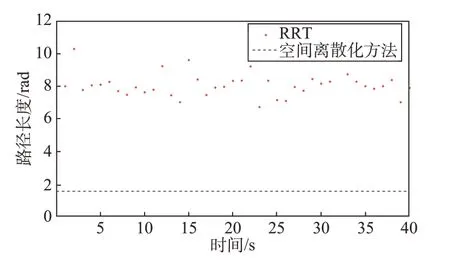
图17 空间离散化方法规划路径长度与RRT方法的40次重复仿真结果对比Fig.17 Path length comparison between space discretization method and results produced by RRT for 40 times
图17 显示本文方法的路径搜索算法具有较好的路径长度优化效果,与RRT 方法的路径结果相比路径长度大大缩短。图18 直观展示了天球坐标系下本文方法与RRT 方法生成的两条路径的对比。强制约束在图中隐去,姿态沿路径机动过程中实际受到强制约束。

图18 敏感器光轴在单位天球惯性系上的指向路径(本文方法与RRT方法结果对比)Fig.18 Path of sensor axis on unit celestial sphere in inertial flame(results compared with RRT)
5 结论
本文通过MRP 参数空间离散化求解了时变指向约束下的姿态规划问题,针对深空条件下姿态机动任务中动态环境约束的情况,提出了一种将三维空间路径搜索算法和逆动力学多项式轨迹规划方法结合的姿态规划方法。为了满足时变指向约束,通过笛卡尔网格划分和边界定义,构建了三维MRP空间中的非奇异空间,实现姿态参数空间离散化和指向约束表征。进一步在Focused D*算法基础上,从非奇异空间搜索和时变约束冲突定位两个方面设计适应于MRP 动态空间的路径扩展策略。利用算法动态避障能力,在路径节点的对应时刻判断约束冲突情况,对路径进行实时修正,最终生成从初始到目标姿态满足时变指向约束的姿态机动执行路径。仿真结果表明,本文姿态参数空间离散化路径规划方法能够处理时变多类型多指向约束的复杂情况,生成安全姿态机动路径。
所提出的姿态规划方法应用于仿真案例时,表现出良好的约束处理能力和路径长度的优化效果。但同时当前方法仍存在一些待解决,且未来值得研究的问题:1)当前路径搜索算法生成的优化路径是以当前节点到起点和终点的距离为评价函数,可以对启发式评价函数进行设计,研究提升规划路径的能量优化效果的改进方法;2)由于Focused D*、D*等图搜索算法需要离散化空间构建,计算复杂度受到离散精细度的影响,未来考虑构建全局规划与局部优化结合的规划架构,研究采用路径搜索算法进行局部路径优化的快速高效的姿态规划方法。
