农业绿色生产效率与经济韧性耦合协调度的时空演变特征
2024-05-26梁坤丽刘维奇
梁坤丽,刘维奇
(1.山西财经大学 经济学院,太原 030006;2.晋中学院 经济管理系,山西 晋中 030032)
0 引言
农业是国民经济的基础产业,其高质量发展事关国家粮食安全和农民增收。然而在农业效益增值乏力、资源环境约束、外部环境不确定性等多重压力下,农业高质量发展面临着严峻的挑战。高质量发展的实质是可持续发展,可持续发展的要求和外部环境的不确定性引起了学者们对效率和韧性问题的关注。农业绿色生产效率主要关注资源环境等约束下的最大产出,而农业经济韧性强调农业在应对不确定性时的恢复、适应和转型能力。若仅考虑效率则系统容易大起大落,若仅探讨韧性则容易导致资源冗余和发展滞后;只有富有韧性又不失效率,才能有效应对系统内外的变化以实现高质量发展。因此,提升农业绿色生产效率、农业经济韧性及二者的耦合协调发展已成为农业高质量发展的重要内容和迫切要求。
与本文相关的文献主要有3类,一是关于农业绿色生产效率的研究,主要集中在两个方面,一方面是农业绿色生产效率评价,有学者倾向于构建更全面的评价指标体系,采用更科学的方法进行综合评价[1];另一方面是影响因素,研究表明环境规制[2]、财政支持[3]等对农业绿色生产效率有显著影响。二是关于农业经济韧性的研究,主要围绕农业韧性的评价、影响因素、影响效应等展开。由于内涵界定并不一致,因此其评价指标体系及评价结果比较多元[4—6],研究发现产业融合有助于农业经济韧性提升进而促进农业高质量发展[4]。三是关于效率与韧性的协同研究,学者们已在能源[7]、水资源[8]和海洋渔业系统开始探索,评价其效率和韧性的协同水平。梳理以往研究成果发现:单独探讨农业绿色生产效率和农业经济韧性的文献较为丰富,但缺乏对二者的动态演进分析;效率与韧性的协同在很多产业开始探索应用,但缺乏在农业领域的相关研究。
鉴于此,本文构建农业绿色生产效率和农业经济韧性指标体系,运用耦合协调度、Markov链等方法,系统评估中国农业绿色生产效率和农业经济韧性耦合协调水平的时空分异、演变趋势及影响因素,力图丰富效率与韧性的协同研究成果,助力农业高质量发展。
1 研究设计
1.1 农业绿色生产效率评价指标体系构建及测度
借鉴已有相关研究[9—11],从投入和产出两个角度来选取指标,见下页表1。采用投入导向、规模报酬不变和全局参比的超效率EBM模型来测度农业绿色生产效率。
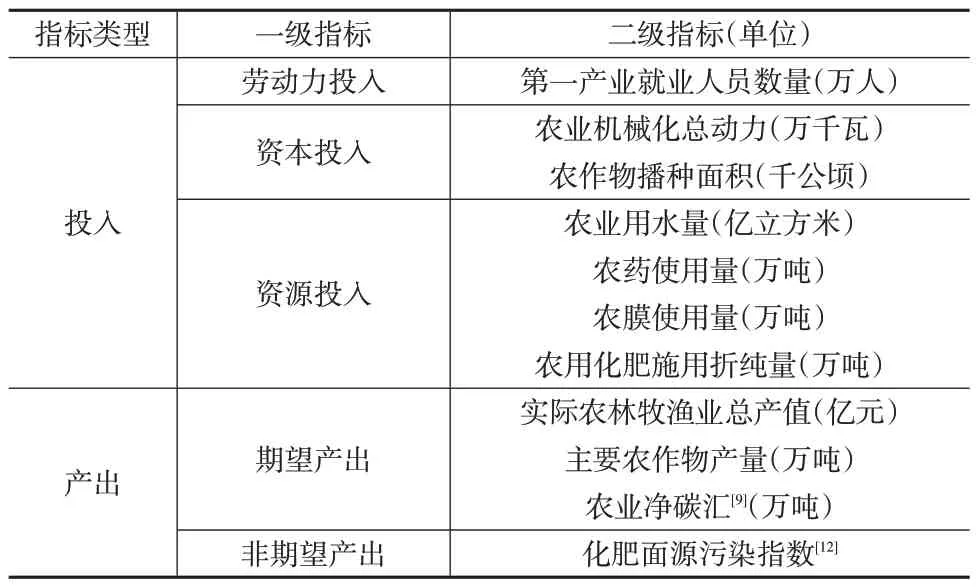
表1 农业绿色生产效率评价指标体系
1.2 农业经济韧性评价指标体系及测度
借鉴已有相关研究[4—6],从农业经济韧性的抵抗恢复、适应调整及转型发展三个能力层面,构建评价指标体系,见下页表2,并采用极差标准化法对原始数据进行标准化处理,运用熵权法计算指标权重并测度农业经济韧性水平。
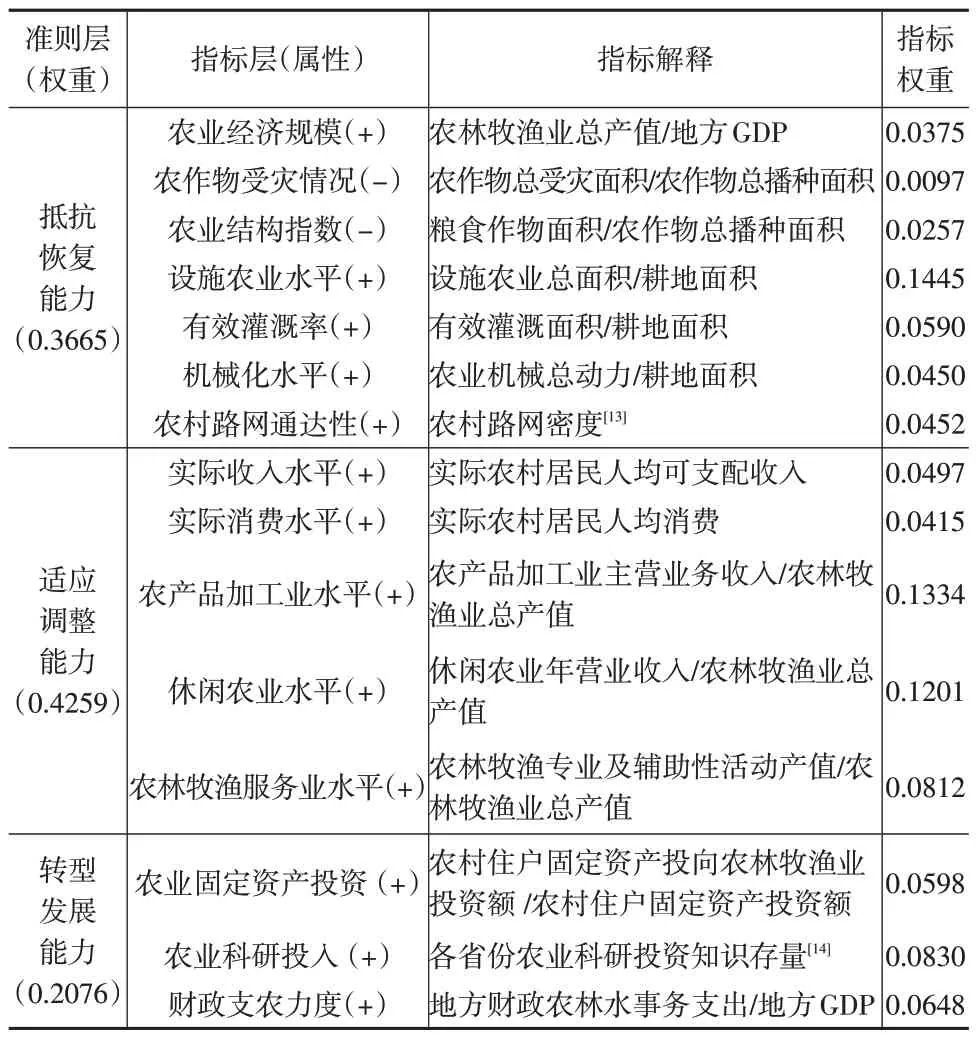
表2 农业经济韧性评价指标体系
1.3 耦合协调度测度
该方法主要用于分析两种以上的系统间相互作用的协同水平。借鉴相关研究[15],考虑到两大系统在农业发展中同等重要,将本文参数设定为0.5。根据计算结果将耦合协调度(Coupling Coordination Degree,以下简称CCD)进行聚类,划分为4 个等级:CCD≤0.4648 为低耦合协调度(L),0.4648<CCD≤0.5485 为中低耦合协调度(ML),0.5485<CCD≤0.6520 为中高耦合协调度(MH),0.6520<CCD≤1为高耦合协调度(H)。
1.4 核密度估计法
本文采用高斯核估计区域农业绿色生产效率、农业经济韧性及二者耦合协调度的核密度曲线以分析其区域差异和时序演变特征。公式如下:
其中,f(x)为x点处的概率密度估计函数,N是观测值的数目,h表示带宽,Xi为独立同分布的观测值,K(·)是核函数。
1.5 Markov链
该方法通过状态转移矩阵描述变量随时间推移至不同状态的转移概率。传统Markov 链假设区域间相互独立,而空间Markov 链弥补了传统Markov 链对空间关联的忽视,揭示变量时空演变特征。本文采用传统和空间Markov链分析不同耦合协调度的区域动态演变趋势。
1.6 数据来源
研究样本选择2008—2020 年我国30 个省份(不含西藏和港澳台)的面板数据,除设施农业面积来源于全国温室数据系统,休闲农业数据来源于历年《中国休闲农业年鉴》外,其他统计数据主要来源于《中国统计年鉴》《中国农村统计年鉴》《中国农业年鉴》、各省份统计年鉴和统计公报、国家统计局数据中心、中国经济与社会发展统计数据库。部分缺失数据采用线性插值法补齐,与价格有关的变量均以2000年为基期对数据进行折算。
2 结果分析
2.1 农业绿色生产效率和农业经济韧性的时空特征
2.1.1 农业绿色生产效率的分布动态
如图1(a)所示,时间趋势上,观察期内全国平均农业绿色生产效率几乎保持不变,年均增长率为0.2%。空间上呈现非均衡特征,东部、西部、东北和中部地区逐级递减,中部地区基本属于“沦陷区”,东北地区平均水平逐渐下降,波动最大。

图1 全国及四大地区的农业绿色生产效率时空分布动态演进
如图1(b)所示,观察期内全国平均农业绿色生产效率分布动态呈现如下特征:第一,核密度分布曲线中心位置随年份的推移未发生明显变化,说明农业绿色生产效率停滞不前。第二,主峰峰值在波动中上升,宽度在波动中变窄,说明农业绿色生产效率集聚程度在上升,绝对差异呈缩小趋势。第三,存在一定程度的右拖尾现象,延展性呈现拓宽后又收窄的趋势,说明农业绿色生产效率最高的省份(江苏)与最低的省份(甘肃)之间的差距在缩小。第四,波峰数量呈明显多峰格局,表明农业绿色生产效率有一定梯度,呈多极分化现象。
图1(c)至图1(f)分别描述了东部、中部、西部及东北地区农业绿色生产效率的动态演进特征。观察可知:各地区波峰位置同全国类似,表明各地区农业绿色生产效率也是停滞不前,但各地区分布形态及波峰数量略有差异。东部地区呈现多峰且波峰宽度变宽,表明东部地区农业绿色生产效率呈多极分化且内部差异扩大。中部地区大多数年份呈双峰格局,表明中部地区农业绿色生产效率呈现比较稳定的两极分化。西部地区呈现多峰—双峰的转变且主峰高度变高、宽度变窄,表明西部地区呈现由多极分化向两极分化转变的态势,且内部差异缩小。东北地区呈双峰状态,波峰宽度逐渐增加,存在一定程度的右拖尾,表明东北地区农业绿色生产效率呈现两极分化,辽宁农业绿色生产效率持续提高,进一步拉大与吉林的差距。
2.1.2 农业经济韧性的分布动态
如图2(a)所示,时间趋势上,观察期内全国农业经济韧性呈现波动上升趋势,年均增长率为5.6%。空间上呈现非均衡特征,东部、东北、中部和西部地区逐级递减,其中,东北地区自2017 年逐渐下降,中部地区增长放缓,而西部地区呈逐渐增长态势,到2020年三者发展水平趋同。
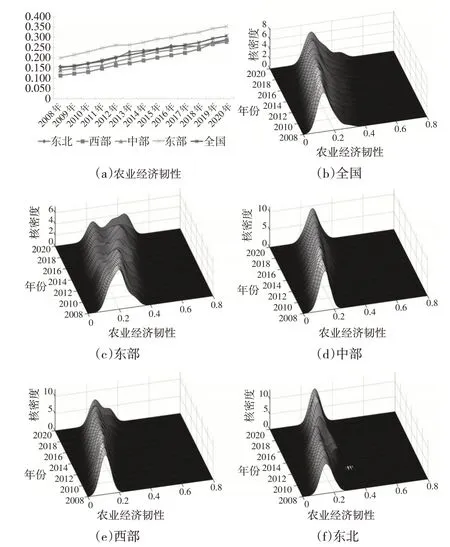
图2 全国及四大地区的农业经济韧性时空分布动态演进
如图2(b)所示,观察期内全国农业经济韧性分布动态呈现如下特征:第一,核密度分布曲线中心位置随年份的推移向右移动,说明农业经济韧性逐渐向高水平演进。第二,主峰峰值在波动中下降,宽度略微变宽,说明全国农业经济韧性离散程度在上升,绝对差异呈扩大趋势。第三,存在一定程度的右拖尾现象,农业经济韧性最高的省份(北京)与最低的省份(广西)之间的差距在缩小。第四,波峰数量呈明显单峰格局,表明农业经济韧性不存在多极分化特征,各地区均衡化发展。
图2(c)至图2(f)分别描述了东部、中部、西部及东北地区农业经济韧性的动态演进特征。观察可知:各地区波峰位置同全国类似,呈现右移趋势,表明各地区农业经济韧性均向高水平演进。但各地区的核密度分布形态及波峰数量略有差异。东部地区波峰呈现单峰—双峰—多峰的发展格局,波峰宽度有变宽的趋势,说明东部地区农业经济韧性逐步呈现多极分化的格局,内部差异在扩大。中部地区波峰呈单峰,延展性在收敛,表明中部地区农业经济韧性最低省份(山西)正向平均水平靠近。西部地区波峰呈单峰—双峰格局且波峰变宽,表明西部地区农业经济韧性呈两极分化,内部差异有扩大的趋势。东北地区波峰呈现单峰—双峰—单峰的发展格局,主峰高度变高,波峰宽度变窄,表明东北地区农业经济韧性在波动中向较高水平集聚,内部绝对差异呈现波动中缩小的趋势。
2.2 耦合协调度分布动态及演进趋势
2.2.1 耦合协调度分布动态
由图3(a)所示,时间趋势上,观察期内全国耦合协调度在波动中上升,年均增长率为5.58%。空间上呈现非均衡特征,东部、西部、中部和东北地区逐级递减。东北地区波动较大,2008年其耦合协调度远高于平均水平,2009年开始波动下降,到2020 年与中部地区水平趋同。西部地区增长最为稳健,由2008年远低于全国平均水平,到2020年超过全国平均水平,并逐步接近东部地区平均水平。
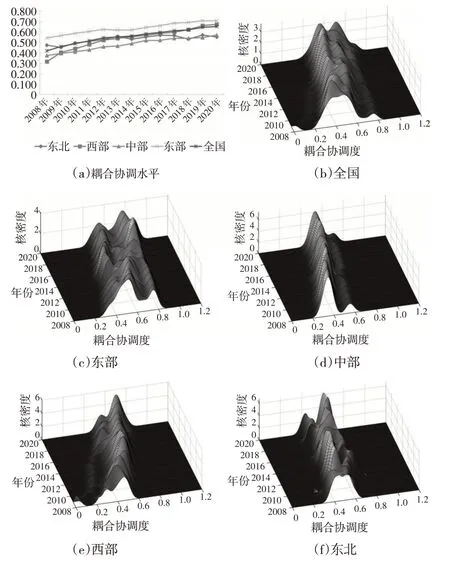
图3 全国及四大地区的农业绿色生产效率与经济韧性耦合协调度分布动态演进
由图3(b)所示,观察期内全国耦合协调度的分布动态呈如下特征:第一,核密度分布曲线中心位置随时间的推移先左移后右移,但整体向右侧移动。说明在观察期内波动频繁,但总体呈现上升趋势。第二,主峰高度先上升后下降,宽度在波动中变宽,说明全国平均耦合协调度的离散程度在上升,其绝对差异随时间推移呈现扩大趋势。第三,呈现一定程度的右拖尾,延展性呈小幅度收敛趋势,说明耦合协调度最高的省份(上海)与最低的省份(甘肃)绝对差距在缩小。第四,波峰数量呈现多峰—双峰变化过程,表明全国耦合协调度有一定的梯度,存在多极分化和两极分化的趋势但分化程度在减弱。
图3(c)至图3(f)分别描述了东部、中部、西部及东北地区耦合协调度的动态演进特征。观察可知:在分布位置方面,东部地区2009—2011 年小幅度左移,之后右移;中部地区小幅度右移;东北地区仅2009年左移;西部地区基本与全国整体趋势保持一致,在波动中上升。在波峰态势方面,东部地区分布形态与全国趋势基本保持一致,即东部地区耦合协调度的离散程度在上升,内部绝对差异呈现扩大趋势;中部地区主峰高度在波动中上升,宽度无明显波动,表明中部地区耦合协调度的集聚程度提升;西部地区主峰高度呈现上升—下降—上升态势,宽度波动中变窄,表明西部地区耦合协调度集聚程度在波动中上升,内部绝对差异随时间推移呈逐渐缩小的趋势。在延展性方面,除东北地区外,其他地区延展性均呈现小幅度收敛趋势,其中西部地区收敛幅度最大,表明这些区域内部水平最高省份与最低省份的差距在缩小。东北地区延展性呈现先收敛后扩展的趋势,说明辽宁耦合协调度继续提高,与吉林差异进一步拉大。在极化趋势方面,东部和东北地区呈现双主峰且高度差别不大,中部地区稳定呈现双峰状态,主峰位置较高,侧峰位置较低,峰值左大右小,无明显变动;西部地区呈现多峰—双峰的变化趋势。表明各地区耦合协调度均呈现多极分化—两极分化的转变趋势。
2.2.2 耦合协调度动态演进趋势
本文将采用Markov链分析全国耦合协调度转移方向及概率,以期进一步考察其动态演进。与前文一致,将全国耦合协调度分为4种类型:低水平(L)、中低水平(ML)、中高水平(MH)及高水平(H),从而得到2008—2020年时间跨度为1年、3年和5年的耦合协调度传统Markov转移矩阵,见表3。
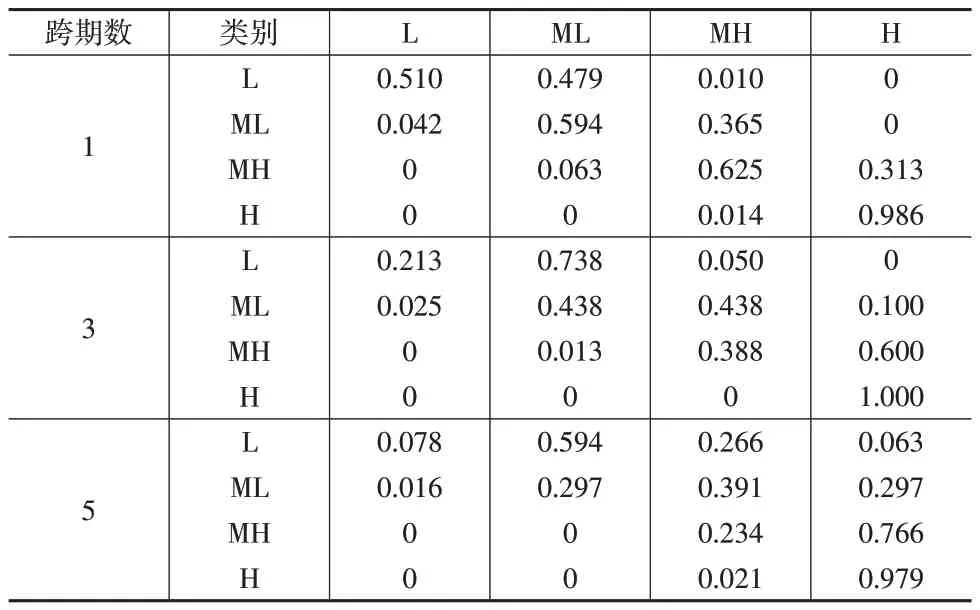
表3 2008—2020年耦合协调度的传统Markov概率转移矩阵
根据表3 测算结果,首先,各类别对角线上概率值并没有显著高于非对角线上的概率值,说明各地区耦合协调度并不稳定,保持始终状态的概率较小,内部流动性较强。在观察期内,当时间跨度为1 年时,不同类别之间转移最大概率发生在L向ML转移方向上,为47.9%,其次为ML向MH转移;当时间跨度为3年时,不同类别转移最大概率仍为L向ML转移,高达73.8%,其次为MH向H转移,为60%;当时间跨度为5年时,不同类型转移最大概率为MH向H转移,高达76.6%。其次,比较各类别对角线上元素与其上三角元素值大小,当时间跨度为3 年时,只有部分对角线上的值小于上三角的元素;当时间跨度为5年时,所有对角线上的值均小于上三角的元素,表明不同耦合协调度地区均能实现等级向上跨越发展。最后,不同耦合协调度地区实现等级向上发展的时间跨度不同,低和中低水平实现等级向上发展的时间跨度为3年,而中高水平则为5年。
表3揭示了耦合协调度动态演进规律,但忽视了耦合协调度往往受到周边地区的影响,因此考虑空间背景,构建跨期为1 年的空间Markov 转移概率矩阵,如表4 所示。
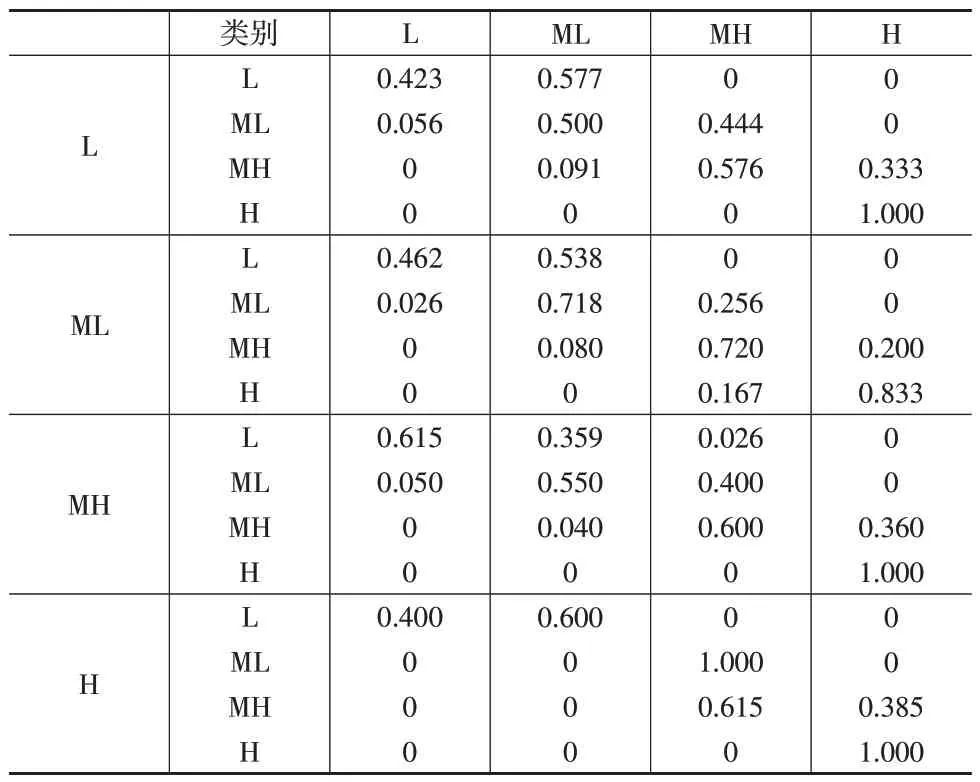
表4 2008—2020年耦合协调度的空间Markov链转移概率矩阵
可以看出:(1)空间效应在各地区耦合协调度动态发展中起着重要作用。在不同类别邻居条件下,耦合协调度类别转移概率各不相同,也不同于相应的传统Markov转移概率矩阵。以耦合协调度的L 地区为例,当跨度为1年,其邻居分别为L、ML、MH 和H 地区时,其保持稳定的概率分别为42.3%、46.2%、61.5%和40.0%,不同于传统情形下的51%。(2)不同邻居水平在不同类别的转移作用不同,存在“以邻为善”和“以邻为壑”情形。以ML 和MH 地区为例,若以耦合协调度高水平地区为邻,则向上提升概率要高于以同水平地区为邻的转移概率,而若与低水平地区为邻,则其向下转移概率也要高于以同水平为邻的转移概率。说明ML 和MH 地区受周围的影响较大,即低水平邻居会拖累本地区耦合协调度提升。但是也存在特例,L 与ML 为邻,向上转移概率反而降低了,说明L 和H地区的耦合协调度可能还受其他因素影响。(3)高水平邻居通过扩散和溢出效应提升低水平邻居的耦合协调度。与高水平为邻时,各地区向上转移的概率均高于传统情形。如以ML 地区为邻时,L 地区向上转移的概率为53.8%,大于传统Markov 链情况下的47.9%;当以MH 地区为邻时,ML 地区向上转移概率同样也高于传统情况。即与不考虑空间因素的情形相比,高水平邻地对本地耦合协调度具有拉动作用。
2.3 耦合协调度的影响因素
借鉴已有相关研究[13,14],选取产业结构、市场规模、环境规制和财政支农作为影响因素,并采用分位数回归方法探讨各因素对耦合协调度的影响。上述影响因素依次选取非农产业占比、社会消费品零售总额、环境污染治理投资总额以及财政农林水事务支出占比来衡量。
表5呈现了各因素对耦合协调度影响的分位数回归结果。结果显示:在25%分位点处,产业结构的影响系数为-0.023,在1%的水平上显著,说明产业结构对低水平耦合协调度有抑制作用;市场规模的影响系数为0.276,在1%的水平上显著,说明市场规模扩大能提升耦合协调度;财政支农和环境规制的影响系数均未能通过显著性检验。在50%分位点处,环境规制的影响系数为-0.156,在5%的水平上显著,说明环境规制不能对中低耦合协调度产生提升作用;市场规模的影响系数为0.167,在10%的水平上显著,说明市场规模扩大能提升耦合协调度;产业结构和财政支农的影响方向均为负,均未通过显著性检验。在75%分位点处,产业结构的影响系数为0.011,在5%的水平上显著,说明产业结构对中高水平耦合协调度有促进作用;环境规制的影响系数为-0.173,在5%的水平上显著,说明环境规制对中高水平的耦合协调度有抑制作用;市场规模的影响系数为0.080,在1%的水平上显著,说明市场规模扩大能提升耦合协调度;财政支农的影响方向为负但未能通过显著性检验。
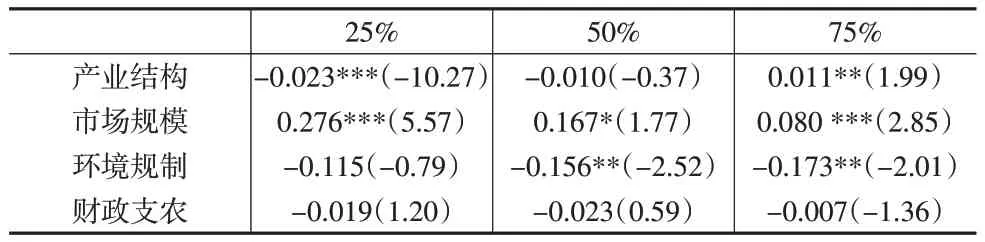
表5 耦合协调度影响因素的分位数回归结果
综上回归结果发现:(1)产业结构对耦合协调度的影响由负转正,可能的原因是产业结构升级未能形成有效反哺,在一定程度上降低了农业生产效率和农业经济韧性[12],而随着耦合协调度进一步提升,产业结构升级通过农村三产融合、农业产业链延伸与拓展,促进了农业生产效率和农村经济韧性的提升。(2)市场规模对耦合协调度的影响显著为正,但存在递减效应。可能的原因是有效且较大的市场需求对农业发展形成需求和供给循环因果链,通过本地市场效应和价格指数效应促进农业快速发展,提升农业生产效率和抗风险能力。而递减效应可能源于农业品很难像工业品实现多样化,造成市场需求扩大缓慢所产生的递减效应。(3)环境规制对耦合协调度的影响呈现负向且程度递增趋势。可能的原因是在无明显技术进步的前提下,环境规制增加农户绿色农药、化肥等的替代成本,制约农业绿色生产效率进而抑制耦合协调度提升。(4)财政支农对耦合协调度的影响为负,且均未通过显著性检验,可能的原因是观察期内财政对农林水务的投资结构与农业需求不匹配[12],或者财政投资效应具有长期性和滞后性,目前效果未能显现。
3 结论
本文通过构建指标体系,测算农业绿色生产效率、农业经济韧性及二者的耦合协调度,揭示其时空演化特征,并探究耦合协调度的影响因素,结果表明:(1)农业绿色生产效率停滞不前,农业经济韧性波动上升,二者的耦合协调度整体不高但逐步提升;东部、西部、中部和东北地区呈现逐级递减的空间非均衡性,西部与东部地区是高水平“凸起”,东北与中部地区是中低水平“塌陷”趋势。(2)耦合协调度在各区域均存在明显的极化特征,但分化程度在减弱;东部地区内部差异有扩大趋势,西部地区呈缩小趋势。耦合协调度保持初始状态的概率较小,内部流动性较强,能够实现3~5年等级向上的跨越式发展。耦合协调度具有显著的空间依赖性,水平高的省份具有正向的空间溢出效应。(3)产业结构对耦合协调度呈现“U”型影响,财政支农和环境规制产生负向影响,市场规模产生正向影响。
