基于分数阶矩和分片Wasserstein距离的鲁棒风险度量优化模型

李伟梅，高雷阜

（辽宁工程技术大学a.工商管理学院，辽宁 葫芦岛 125105；b.运筹与优化研究院，辽宁 阜新 123000）

0 引言

风险度量是反映决策者对小概率、高成本极端事件态度的方法，依赖于随机变量的概率分布。在通常情况下，随机变量的真实分布未知，在根据历史数据获得估计分布的过程中，分布尾部模型误差造成的尾部风险偏差在实际决策问题中会造成严重的后果。因此，强化一般风险度量方法对分布尾部不确定性的稳健捕捉能力至关重要。

鲁棒风险度量是通过在一组潜在分布中寻找最坏情况风险值来解决分布不确定的稳健优化方法。潜在分布逼近真实分布所需满足的分布特征条件由其不确定集描述，矩信息是不确定集的主要内容。Mnatsakanov（2008）[1]指出，高阶矩可以获取关于分布的进一步信息，其在复杂优化问题中会存在很大的统计误差。分数阶矩理论上含有大量整数阶矩的信息，可以避免高阶整数矩的误差问题。针对分数阶矩的复杂数值积分计算问题，Alibrandi 和Mosalam（2018）[2]通过定义分数阶序列给出了解决方法，扩展了分数阶矩的使用范围。Zhang 等（2020）[3]在最大熵分布估计模型研究中验证了分数阶矩相比高阶整数矩能够更准确地表示概率分布尾部。综上，精细刻化分布尾部特征离不开分数阶矩，但目前鲜有研究在鲁棒风险度量中引入分数阶矩来优化尾部风险度量的精准性。

基于矩信息估计的分布很难完全符合真实分布，分布模型存在误差不可避免，量化模型误差是鲁棒风险度量不可或缺的内容，而参考分布和分布距离是其中最为重要的两个因素。一般而言，参考分布会选择经验分布或已知的参数分布，其参数由基于3σ原理的极大似然估计得到，分布尾部估计误差不被作为主体考虑，存在低估尾部厚度的可能。错误的分布假设和不完善的估计会带来危害性很大的尾部模型误差，导致的尾部风险度量偏差在实际问题中会引发很严重的后果。因此，构建能有效反映真实分布尾部行为的参考分布对准确描述分布尾部模型误差至关重要。分布距离度量作为定义不确定集的主要方式，决定了哪些分布可以作为潜在分布，可用于刻画分布模型误差。Glasserman 和Xu（2014）[4]将相对熵视为潜在分布合理的指标，量化了分布误差对风险度量的影响。Kruse等（2019）[5]在其研究中解析说明了相对熵的局限性，并得到其不适用于重尾分布的结论。Feng（2019）[6]在模型风险的研究中，针对相对熵的局限性，指出用Wasserstein 距离替代相对熵刻画分布模型误差有明显的效果。但根据Rodríguez 等（2021）[7]的研究，Wasserstein 距离中成本函数的选择会造成概率分布几何结构被忽略，得到的结果可能是次优的，存在两个分布整体Wasserstein距离很小但分布尾部结构不同的可能，而尾部反映对识别真实分布十分重要。因此，基于Wasserstein距离的分布尾部模型误差问题仍需细化研究。

鉴于此，本文以提升一般鲁棒风险度量优化模型精准性为目标，克服一般参数分布不能刻画分布尾部行为的限制，强化风险度量对分布尾部不确定性的精细刻画能力，从分布尾部信息刻画和误差量化两种角度改进鲁棒风险度量模型，为突发性极端风险度量提供参考。

1 理论方法概述

1.1 鲁棒优化方法

令X={x1，…，xN}为离散型随机变量，P={p1，…，pN}为X在支撑集Ω上的未知概率分布。令Z={z1，…，zN}为将X映射到[0,1]内的随机变量，其在支撑集S上的概率分布为Q={q1，…，qN}。以通常的指数分布簇为基准，当Q=exp(-β(Z))，β(Z)～ρZt，t∈R 为形状参数，ρ∈R 为尺度参数时，分布Q的尾部行为取决于ρ和t[5,8]。

对于随机变量Z，一般的鲁棒风险度量模型为：

其中，v(Z)表示与随机变量Z相关的损失函数，Γ 为随机变量Z的分布不确定集。文献[9]给出了几种构建Γ的方法，矩信息和分布距离是其中最主要的内容。

1.2 分数阶矩与分布距离度量方法

随机变量Z的分数阶矩[10]为：

其中，α={α1，…，αK}，αk∈R，k=1，…，K。少量低阶分数阶矩能捕捉分布尾部信息并保留分布的某些结构，在数值算例中具有稳定性。

Wasserstein 距离[11]作为最优传输的特例，可度量非绝对连续分布距离，令={，…，}为样本数据估计的参考分布，则概率分布Q和参考分布之间的离散Wasserstein距离为：

其中，Y=(y1，…，yN)～，c(Z，Y)为传输成本，γ(Z，Y)是分布Q和Q^ 的联合分布，Π 是所有可能联合分布组成的集合，γ(Z，Y)满足以下性质。

Wasserstein距离克服了相对熵的局限性，可度量任意两个概率分布之间的距离。在高维样本数据的计算中，由于分布不能可数离散化，因此集合势比较大，Wasserstein距离估计会遭遇维数灾难。熵正则化的Wasserstein 距离[12]简化了其计算复杂度，并将最优传输问题转化为一个严格凸问题，能更合理地表示分布的不确定性，具体表达式如下：

其中，φ∈R 为调节熵正则化惩罚力度的系数。

2 鲁棒风险度量

2.1 概率分布估计模型

鲁棒风险度量优化离不开参考分布，在参考分布估计方法中，文献[13]基于分数阶矩信息给出最大熵概率分布估计模型，用于提升对分布尾部不确定性的估计能力。模型如下：

最大熵分布是在已知部分信息的情况下，对未知分布不添加任何其他约束的分布估计方法，存在较大的分布模型误差。因此，为了提高概率分布尾部的估计精度，在此模型的基础上，引入Wasserstein 距离度量分布模型误差，建立基于分数阶矩和熵正则化Wasserstein 的概率分布估计模型：

其目标函数和约束函数关于γ(Z，ξ)可微，且一阶导数连续，满足约束规范条件[14]，Lagrange对偶问题为：

其中，λ={λ1，…，λk}，v是Lagrange 乘子。根据Lagrange对偶理论，可得模型（10）的最优解为：

根据公式（5），模型（8）的最优解={，…，}可以表示为：

其中，λ，v，α可通过求解以下模型得到：

在本文提出的概率分布估计模型中，分数阶矩增加了能更精细刻画分布尾部的约束性，熵正则化Wasserstein距离解决了分布模型误差刻画和非凸优化的凸松弛问题，两者结合有助于概率分布尾部精细化估计，根据此模型可以精准地确定随机变量Z的参考分布。

2.2 基于分数阶矩和Wasserstein距离的鲁棒风险度量模型

基于矩约束且考虑模型误差的一般鲁棒风险度量模型为：

鲁棒风险度量模型对概率分布尾部不确定性的捕捉能力依赖于矩约束E[(Z)β]=μβ，模型误差取决于D(Q|Q^)。鉴于少量低阶分数阶矩能克服高阶整数矩的数值不稳定性刻画分布尾部，熵约束的Wasserstein距离能够突破相对熵的局限性有效量化模型误差，建立如下鲁棒风险度量模型：

其中，Y={y1，…，yN}～，为公式（12）确定的概率分布估计结果,ε1，ε2为给定的分布模型误差阈值。根据文献[6]的研究，上述模型等价于：

将分数阶α视为参数，对于γ(Z，Y)而言，上述模型满足约束规范条件和强对偶性，其Lagrange对偶问题为：

其中，η={η1，…，ηk},σ,κ，ρ是Lagrange 乘子，σ反映Wasserstein 距离约束对目标函数的影响。根据Lagrange对偶理论，可得模型（18）的最优解为：

其中，η,σ,κ可通过优化以下模型得到：

2.3 基于分数阶矩和分片Wasserstein 距离的鲁棒风险度量模型

在鲁棒风险度量模型（15）中，由于Wasserstein距离会忽略分布几何结构，而尾部结构反映的信息对识别真实分布极其重要，结合最坏情况分布公式（19）可知，分布尾部结构依赖于Wasserstein距离成本函数的选择，适合度量整体分布模型误差的Wasserstein距离不一定适合度量分布尾部差异，对分布尾部差异特设一种局部Wasserstein距离对于强化鲁棒风险度量对尾部不确定性的捕捉能力是非常有必要的。

根据纤维丛理论思想[15]，本文提出分片Wasserstein距离，针对分布的不同部分用不同纤维丛来度量分布的差异，从而达到对分布尾部和整体模型误差进行控制与优化的目的。具体地，将随机变量Z的分布支撑集S分割成M个子支撑集Sm，m=1，…，M,。考虑到样本数量对参数优化的影响，选择有针对性的非均匀分段或者均匀分段方式，取M=1，2，…，选择逼近效果最优的分段数。在子支撑集上定义具有不同成本函数的Wasserstein距离：

其中，Pm=prop{Z∈Sm}可由样本数据计算得到，Qm和分别是Z在Sm上的概率分布和参考分布。在每个支撑子集Sm上，基于分数阶矩和Wasserstein距离的鲁棒风险度量模型（22）的求解方法与模型（15）类似，得到子支撑集上的鲁棒风险度量最坏情况分布为：

由全概率公式可得鲁棒风险度量模型（15）的最坏情况分布为：

即通过建立分片鲁棒风险度量模型（22）获得了鲁棒风险度量模型（15）的最优解。

2.4 分数阶矩积分求解方法与算法

在Lagrange 乘子和分数阶的优化模型（13）和模型（20）中，目标函数关于Lagrange 乘子是线性的，但关于分数阶α是非线性的，且无法保证凸性，分数阶最优解不具有唯一性，且分数阶积分运算复杂。针对这一问题，定义分数阶序列{α1，…，αQ}可有效解决上述问题。

其中，Q≥2，αmax为分数阶的最大值。参考文献[10]证实，随着Q的增大，分数阶序列{αj}，j=1，…，Q具有较好的收敛性。

在分片鲁棒风险度量模型（22）中，分数阶矩约束和分片数M 使得需要优化的参数增多，且分数阶积分运算复杂。海鸥优化算法（Seagull Optimization Algorithm，SOA）[16]是一种鲁棒全局优化算法，相比遗传算法具有高效处理高维复杂问题的能力。因此，本文采用SOA求解最优分数阶矩和Lagrange乘子。

3 数值实验

假设随机变量Z的真实分布是Weibull（1，1.5），生成服从Weibull（1，1.5）的数量为1000的随机样本，作为获取真实分布信息的历史数据，模型优化过程在MATLAB R2019a上完成。

3.1 概率分布估计模型有效性验证

在基于分数阶矩和Wasserstein 距离的概率估计模型（8）中，假设分数阶矩的个数K=2，取φ=10,αmax=2，为了验证模型（8）的有效性，采用SOA计算以下三种模型的分布估计结果：（1）基于分数阶矩的最大熵分布估计模型（7）；（2）经验分布估计[17]；（3）基于分数阶矩和熵正则化Wasserstein距离的概率估计模型（8）。得到的分布估计结果如图1所示。

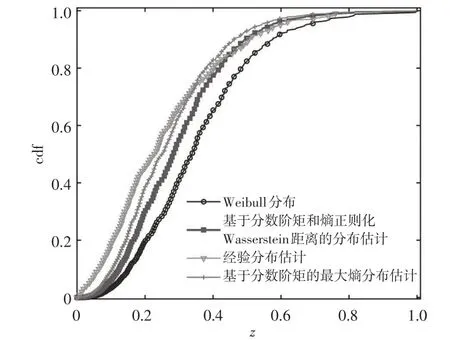
图1 分布估计结果对比

由图1 的分布估计结果可知，相比经验分布估计，基于分数阶矩的最大熵分布估计在分布的尾部提供了更高的估计精度。这表明引入分数阶矩提高了概率分布尾部的估计精度。相比于基于分数阶矩的最大熵分布估计模型，基于分数阶矩和熵正则化Wasserstein距离的分布估计模型（8）能够更好地逼近理论Weibull分布的尾部，这说明引入Wasserstein 距离能够更精细地刻画分布尾部的约束性。因此，当随机变量服从Weibull分布时，本文提出的概率分布模型更适合作为参考分布来反映分布尾部的不确定性信息，该模型在分布尾部的估计精度和逼近性能上都优于其他方法。

为了进一步验证概率估计模型（8）的精确性，计算三种不同分布估计模型的最优分布估计结果与理论Weibull分布之间的均方误差（MSE），结果如表1所示。

表1 分布估计误差

根据表1的分布估计误差结果可知，基于概率估计模型（8）得到的最优分布估计结果与理论Weibull 分布之间的MSE 较小，为0.2130；而其他两个模型的MSE 分别为0.2212 和0.2135。较小的MSE 误差意味着该模型能够更准确地逼近目标分布，并提供更可靠的概率估计结果。这表明概率估计模型（8）相比于其他模型，在对理论Weibull分布的拟合精度上具有更好的表现。

3.2 基于分数阶矩和Wasserstein 距离的鲁棒风险度量模型有效性验证

在基于分数阶矩和Wasserstein 距离的鲁棒风险度量模型（15）中，为了探究分数阶矩在提升度量极端风险精度方面的有效性，假设αmax=2，v(z)=-z，c(z，y)=‖z-y‖2，ε1=ε2=0.1，设置鲁棒风险度量模型（15）的以下三种情境进行对比分析。情境1：K=2，α∈R+。情境2：K=1，α∈R+。情境3：K=2，α={1，2}。

采用SOA分别求解不同情境下模型的最坏情况风险，结果如表2所示。

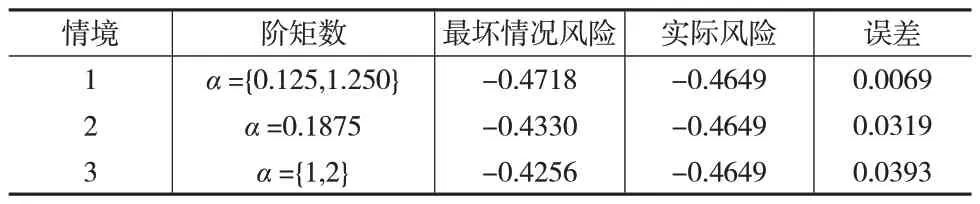
表2 鲁棒风险度量最坏情况风险

分析表2的结果可以发现，当随机变量Z服从Weibull分布时，对比情境2和情境3中最坏情况风险与实际风险之间的误差可以发现，情境2在单个分数阶矩约束的情况下具有更高的风险度量精确性。这说明相较于整数阶矩，分数阶矩更有助于鲁棒风险度量模型（15）准确刻画风险。对比情境1和情境2，以及情境1和情境3的结果时发现，情境1 中两个分数阶矩约束下的风险度量误差最小，这表明在计算鲁棒风险度量模型（15）时，将分数阶作为参数，并选择合适的分数阶矩是有意义的。

计算鲁棒风险度量模型（15）在三种情境下的最坏情况分布，得到的结果如图2所示。

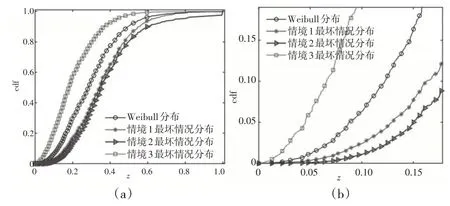
图2 鲁棒风险度量最坏情况分布

根据图2（a）可知，情境1中鲁棒风险度量模型（15）的最坏情况分布整体上更接近随机变量的理论Weibull 分布，说明在模型（15）中引入合适的分数阶矩能够有效获取随机变量整体分布的信息。另外，根据图2（b）可知，分数阶矩的引入显著提升了风险度量模型对分布尾部不确定性的捕捉能力。

为了进一步探究鲁棒风险度量模型（15）的最坏情况风险对分数阶α和Wasserstein距离约束水平σ的敏感性，给定参数η=(η1，…，ηk),κ，ρ的值，在这种情况下，最坏情况风险和α，σ之间的关系如图3所示。

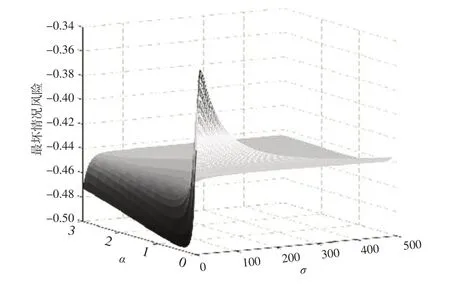
图3 鲁棒风险度量最坏情况风险敏感性分析

从图3可以观察到，在分数阶α和Wasserstein距离约束水平σ处于其最优值邻域范围时，鲁棒风险度量模型（15）的最坏情况期望有显著变化，相比于分数阶α，Wasserstein距离约束水平σ对模型的最坏情况风险具有更大的影响。这意味着选择能进一步精细刻画分布误差的Wasserstein 距离对于提高鲁棒风险度量模型（15）的精确性是有意义的。

3.3 基于分数阶矩和分片Wasserstein 距离的鲁棒风险度量模型的有效性验证

固定α={0.1875，1.875}，选取均匀分段方式，令每段的Wasserstein距离的成本函数均为c(z，y)=‖z-y‖2，计算模型（22）在M取不同值时的最坏情况风险，结果如表3所示。

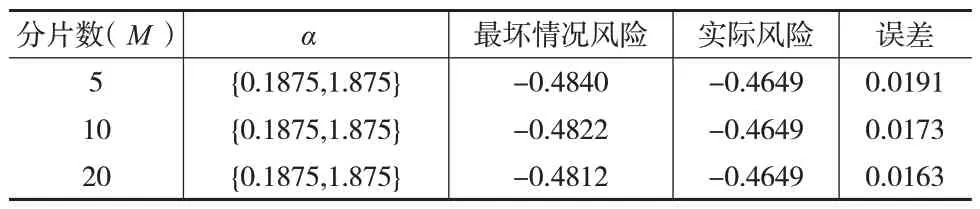
表3 分片鲁棒风险度量最坏情况风险

观察表3 可知，随着分片数的增加，分布鲁棒风险度量模型（22）的最坏情况风险越来越接近真实风险，这说明引入分片Wasserstein 距离有助于提高鲁棒风险度量模型（22）的精确性。

计算模型（22）在M取不同值时的最坏情况分布，结果如图4所示。

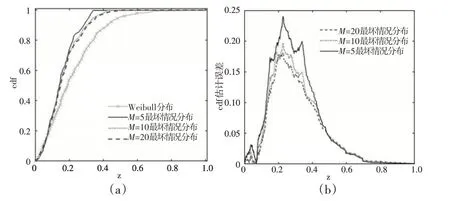
图4 分片鲁棒风险度量最坏情况分布

从图4（a）和（b）中观察到，随着分片数M的增加，鲁棒风险度量模型（22）的最坏情况分布与真实分布的逼近程度提高，特别是在分布尾部的逼近程度显著提升。这说明，引入分片Wasserstein距离有助于改善模型对分布尾部的估计误差，提供更准确的风险度量结果。综上所述，分片Wasserstein 距离有助于提高最坏情况分布与真实分布的逼近程度，尤其是分布尾部的逼近程度，这对于改进和优化风险度量模型具有重要意义。

4 结束语

本文针对已有的鲁棒风险度量模型关于分布尾部不确定性的度量问题，以一种对尾部模型误差具有稳健性的方式建立鲁棒风险度量优化模型，在构造模型不确定集时，提出基于Wasserstein 距离的分布估计参考方法，突破了已有参数分布无法反映真实分布尾部行为的限制。鉴于分数阶矩具有对分布尾部信息的精准刻画能力，本文在解析分布估计的基础上建立基于分数阶矩和Wasserstein距离的鲁棒风险度量优化模型。为优化Wasserstein 距离忽略分布几何结构造成的尾部模型误差，本文基于纤维丛理论思想，引入分片Wasserstein距离解析约束的分片鲁棒风险度量模型。数值实验的结果表明，分数阶矩能够精细刻画分布尾部误差，分片Wasserstein距离能够有效地解析约束控制整体误差以优化求解。相比于传统的鲁棒风险度量模型，分片鲁棒风险度量模型更有助于风险管理者做出最优决策。