超高维数据下部分线性可加分位数回归模型的变量选择
2024-05-26白永昕钱曼玲田茂再
白永昕,钱曼玲,田茂再
(1.北京信息科技大学 理学院,北京 100192;2.墨尔本大学 数学与统计学院,澳大利亚 墨尔本3010;3.中国人民大学应用统计科学研究中心,北京 100872;4.新疆财经大学 统计与信息学院,乌鲁木齐 830012;5.昌吉大学 数学与数据科学学院,湖南 昌吉 831100)
0 引言
随着数据获取技术的发展,在微阵列、蛋白质组学、大脑图像等领域都出现了超高维数据。在超高维数据中,协变量的维数可能远远大于样本量,这给传统的统计方法带来了挑战。高维数据通常是异质的,协变量对条件分布中心的影响可能与他们对尾部的影响大不相同。因此,只关注条件均值函数可能会产生误导。分位数回归通过估计不同分位数水平上的条件分位数,能够更完整地反映协变量和响应变量之间的关系,而且分位数回归对异常点有很强的鲁棒性,在重尾分布下也会得到稳健的估计。部分线性可加模型[1]作为一种半参数回归模型,比参数模型更灵活,比非参数模型更有效。在复杂数据下研究部分线性可加分位数回归模型的变量选择问题具有非常重要的理论和实际意义。
近年来,部分线性可加分位数回归模型引起了学术界的广泛关注。针对模型中线性部分的变量选择问题,一些研究者探索了不同的方法。例如,陈秀平和蔡光辉(2021)[2]使用非负Garrote方法选取重要变量;白玥和田茂再(2017)[3]、宋瑞琪等(2019)[4]系统对比了多种惩罚回归方法(如Lasso、自适应Lasso、SCAD、Elastic Net、组Lasso、组SCAD等)在不同自变量相关性和误差项方差条件下的性能;Mazucheli等(2022)[5]则对线性分位数回归模型的相关研究进行了全面回顾。在高维数据分析场景中,尽管非凸惩罚,如SCAD 和MCP 具有更好的适应性,但其复杂的性质加大了优化难度。为此,Wang 和Zhu(2016)[6]提出了适用于最小二乘回归的arctan型惩罚,它相较于L0惩罚表现出更强的稳定性及Oracle 性质。Li 和Zhu(2008)[7]基于KKT 条件设计了Lasso 惩罚下的分位数回归参数估计算法;而Wu和Lange(2008)[8]探讨了中位回归的快速贪婪坐标下降算法;Wang等(2012)[9]进一步将局部线性算法运用到非凸惩罚的分位数回归参数估计中,但该方法在高维协变量下的计算效率偏低。为应对计算效率问题,Peng 和Wang(2015)[10]研发了针对非凸惩罚的迭代坐标下降算法(Iterative Coordinate Descent Algorithm,QICD),并证明了它的收敛性。模拟实验显示,即使在极高维的情况下,QICD算法依然有效。在此基础上,Sherwood 和Maidman(2022)[11]利用QICD算法对可加分位数回归模型进行了变量选择和相关参数估计。
总体来看,现有文献对部分线性可加分位数回归模型变量选择的研究已较为丰富,但仍存在一定的局限性:一是现有研究主要集中于协变量维度是固定的情况;二是并未同时考虑线性部分和可加部分的稀疏性。鉴于此,本文考虑了协变量维度发散情况下的部分线性可加分位数回归模型,通过双惩罚方法对模型中的线性部分和可加部分进行变量选择和稳健估计,并推导了估计量的渐近性质,以期推动该问题的研究进展,获得对部分线性可加分位数模型估计问题更深入、更全面的理解。
1 部分线性可加分位数回归模型
假定{(Yi,xi,zi):i=1,…,n} 是独立同分布样本,Yi是响应变量。本文考虑协变量维度随样本量n变化的情况。记pn为随样本量变化的协变量维度,xi=(xi1,…,)和zi=(zi1,…,zid)分别是参数部分和非参数部分的协变量向量。给定(xi,zi),Yi的条件分位函数为=inf{t:F(t|xi,zi)≥τ},其中,F(·|xi,zi)是Yi的条件函数。考虑如下部分线性可加分位数回归模型:
2 部分线性可加分位数回归模型的双惩罚估计
2.1 基于Atan双惩罚的估计
在实际数据中,通常并不知道哪些变量是重要变量。为了得到稀疏的估计量,最小化如下惩罚目标函数:
其中,P(β,γ)表示关于参数β以及非参数函数gj的惩罚函数。为了构造一个在保证模型稀疏性的同时还能保证估计函数光滑性的估计量,本文提出了Atan 双惩罚函数:
2.2 渐近性质
条件(1)是分位数回归中使用的标准假设。条件(2)对于B样条基函数是必要的,它可以用来有效地逼近满足Holders条件的函数。条件(3)是一个可识别条件,对Oracle模型下的协变量和设计阵进行了约束。假设xi四阶矩有界就足够了。条件(4)给出了用B样条逼近非参数部分时样条基的维度。条件(5)给出了β最小非零项个数的下限。条件(6)对Atan 双惩罚中的调整参数λ1和α进行了约束,类似的约束可参见文献[6]。条件(7)限制了双惩罚函数的一阶导数和二阶导数的变化速度。条件(8)用于证明Atan 估计的渐近正态性,与Lindeberg-Feller 中心极限定理中的Lindeberg条件有关。
定理1:假设正 则条件(1)至 条件(8)成立,则∀η∈(0,1),∃常数C>0,使得:
定理2:假设正则条件(1)至条件(8)成立,则:
3 算法
交替迭代算法的步骤如下:
在步骤2.2中,Atan惩罚很显然是非凸函数,可以用它的一阶泰勒近似代替非凸惩罚值,得到一个在当前值β(t)处的凸目标函数,即。本文使用分位迭代坐标下降算法对步骤2.2中的目标函数进行最小化,限于篇幅,算法的具体步骤省略。
4 模拟研究
本文通过模拟研究对所提方法的性能进行研究,并将其与现有方法(Lasso、SCAD和MCP惩罚)进行比较。为了减轻计算负担,将SCAD、MCP 以及Atan 双惩罚中的参数分别设置为a1=3.7、a2=2.7 以及a3=0.005。对于样本量和协变量维度,考虑n=200 和pn=100,500。在模拟研究中,重复模拟100次并考虑3个不同的分位点τ=0.3,0.5,0.7。
考虑如下模型:
对于参数估计的精度,通过以下指标进行评价:(1)均方误差(MSE):通过MSE 来衡量参数估计的精度。(2)在一个由均匀分布在[0,1]上的500 个点(t1,…,tT)组成的细网格上计算两个分量函数的均方根误差(RMSE),通过MSE来评估非参数函数的性能。在计算中,若参数估计值小于1e-06,则默认其值为0。
对于随机误差项的分布,考虑如下三种不同的情形:(1)标准正态分布;(2)自由度为3的t 分布;(3)异方差的正态分布,即ϵi=Xi1ζi,其中,ζi~N(0,1) 且与Xi相互独立。不同误差分布下的模拟结果见表1至表3。
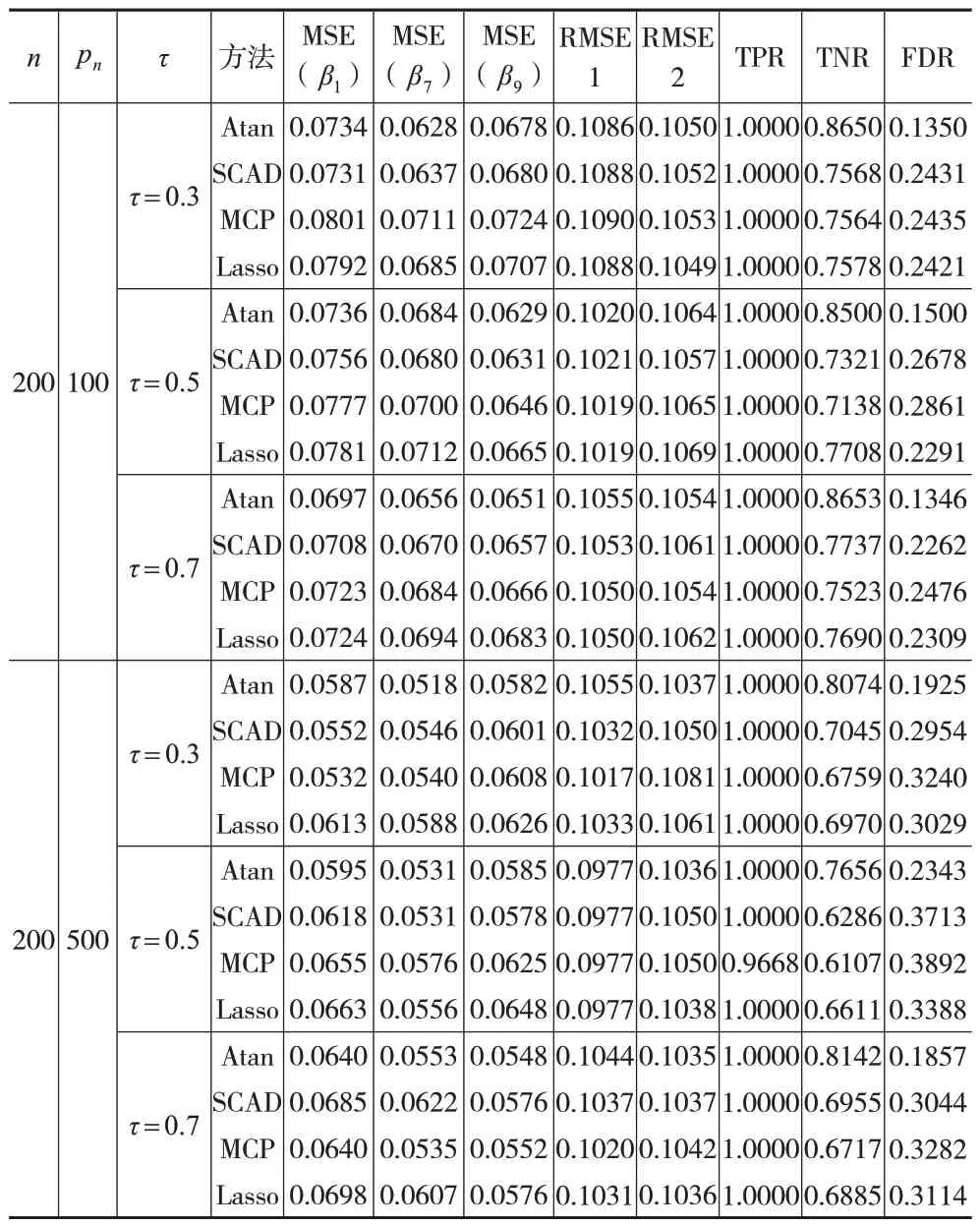
表1 随机误差项ϵ~N(0,1)情况下的模拟结果
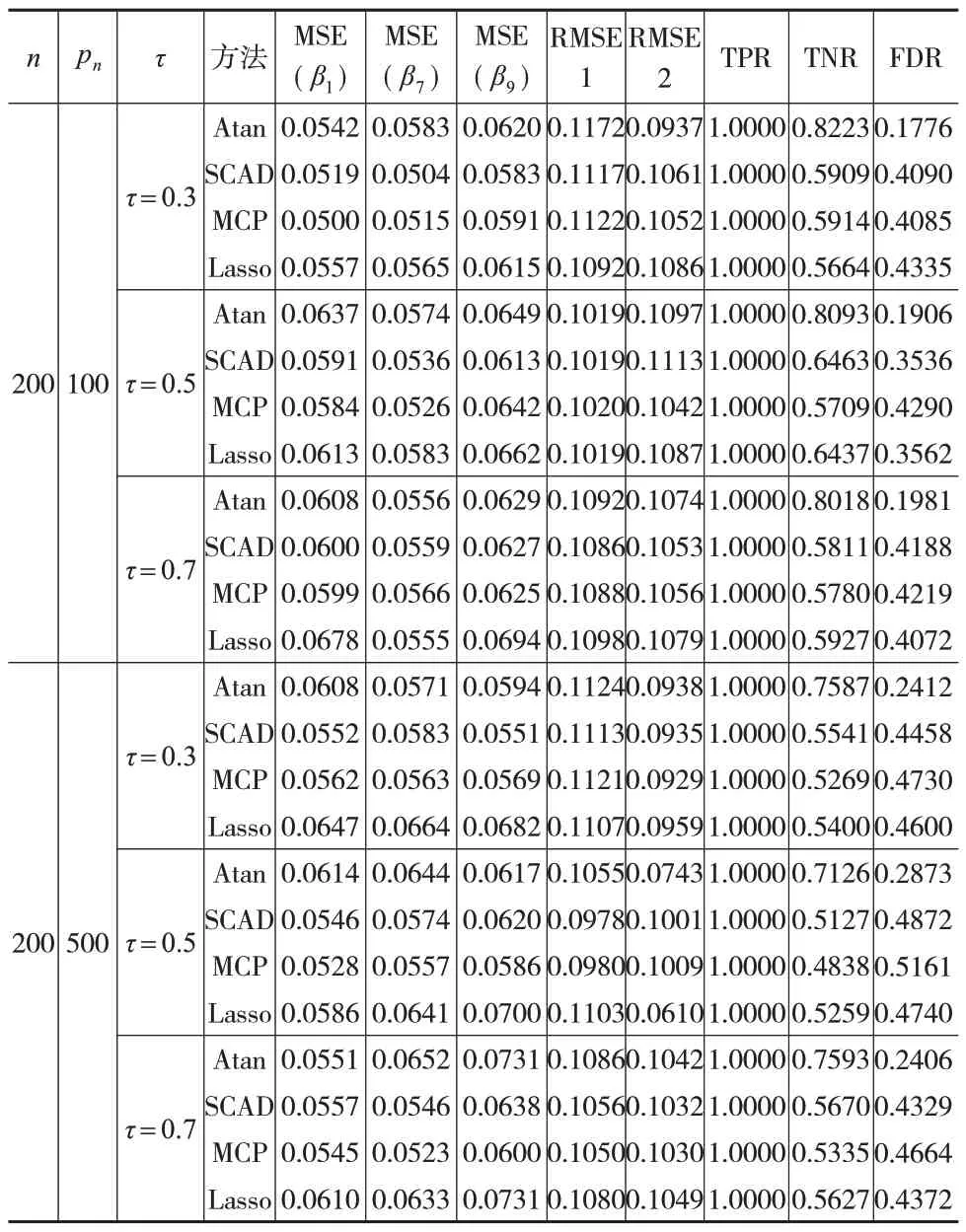
表2 随机误差项ϵ~t(3)情况下的模拟结果

表3 随机误差项ϵ~Xi1ζi, ζi~N(0,1) 情况下的模拟结果
从表1 至表3 可以看出,在不同随机误差项分布和不同pn值下,所有方法对非线性部分的拟合都比较相似。同时,在变量选择上,这些方法的TPR都在1左右,说明所有方法都可以选择重要的变量。进一步观察发现,在大多数情况下,特别是当随机误差项服从标准正态分布时,本文所提Atan 双惩罚估计量的MSE 小于其他惩罚的估计量,这可能是因为Atan 双惩罚估计量是无偏的。同时,Atan 双惩罚估计量不正确筛选重要变量的比例相比其他方法也更低。更重要的是,当随机误差项服从t分布和异方差的正态分布时,其他惩罚估计量的TNR显著下降,主要集中在0.5 左右,而Atan 双惩罚估计量的TNR 保持在0.8左右。与此同时,其他惩罚估计量的FDR逐渐上升,而Atan 双惩罚估计量的FDR 大部分保持在0.2 附近。不可忽视的是,本文所提方法以较大的MSE为代价,选择了更精确的模型。总之,当随机误差项服从重尾分布和异方差分布时,本文所提Atan双惩罚的性能更好。
5 实证分析
将本文提出的Atan 双惩罚方法应用于一个包含315个癌症筛查病人的血液样本数据集。该数据集来源于http://lib.stat.cmu.edu/datasets/Plasma_Retinol,主要记录了每个病人的β-胡萝卜素血浆浓度、年龄、性别、体重、是否抽烟饮酒等14 个变量的数据。已有研究表明,血浆中的β-胡萝卜素含量与患一些特定类型癌症的风险相关,因此本文的目标是找到影响β-胡萝卜素血浆浓度的变量。Guo等(2013)[14]研究发现,Age(年龄)、Chol(每天摄入的胆固醇)和Fiber(每天摄入的动植物纤维)与血浆β-胡萝卜素水平存在非线性关系,其他变量则与血浆β-胡萝卜素水平存在线性关系。因此,本文考虑采用部分线性可加分位数回归模型对标准化后的数据集进行变量选择。表4 给出了不同惩罚下变量选择的结果,其中,协变量分别为Quet(体重/身高的平方)、Calor(每天摄入的卡路里)、Fat(每天摄入的脂肪)、Alco(每周摄入的酒精)、Betad(每天摄入的β-胡萝卜素)、Retd(每天摄入的视网醇)、Retpl(视网醇血浆浓度)、Sex(性别)、Smok(是否抽烟)、Vit(是否经常使用维生素)。图1给出了三个非参数成分在不同分位数下的估计曲线。从表4可以看出,在Lasso 惩罚下,协变量Fat和Retd未被选出,但是其他三个非凸惩罚均选出了这两个协变量。同时,三种非凸惩罚的结果相似,但SCAD 和MCP 惩罚法高估了协变量Fat和Retd。Fat和Retd对变量选择结果的影响相对较小。

图1 不同分位数下年龄、摄入纤维、胆固醇的估计曲线

表4 不同惩罚下变量选择的结果(τ=0.5)
为了进一步评估本文方法的性能,将数据集随机分为样本量为215的训练集和样本量为100的测试集。重复模拟100次并计算预测误差。表5给出了100次模拟下不同筛选方法在0.3,0.5,0.7 分位点处选择的平均变量数量以及预测误差,反映了模型的平均复杂程度和预测能力;括号内的值为相应的标准误,反映了不同方法在100次重复模拟中的波动性。从表5 可以看出,在不同惩罚下,选出的模型往往不同。在Lasso惩罚下选出的模型比在非凸惩罚下选出的模型复杂程度更低,但同时预测精度也更低。对比三种非凸惩罚可以发现,本文提出的Atan 双惩罚方法比SCAD 和MCP 惩罚预测精度更高,而且标准差也更小,即本文方法更稳定。综合来看,基于Atan双惩罚的变量选择结果较为理想,是一种相对稳健的惩罚方法。
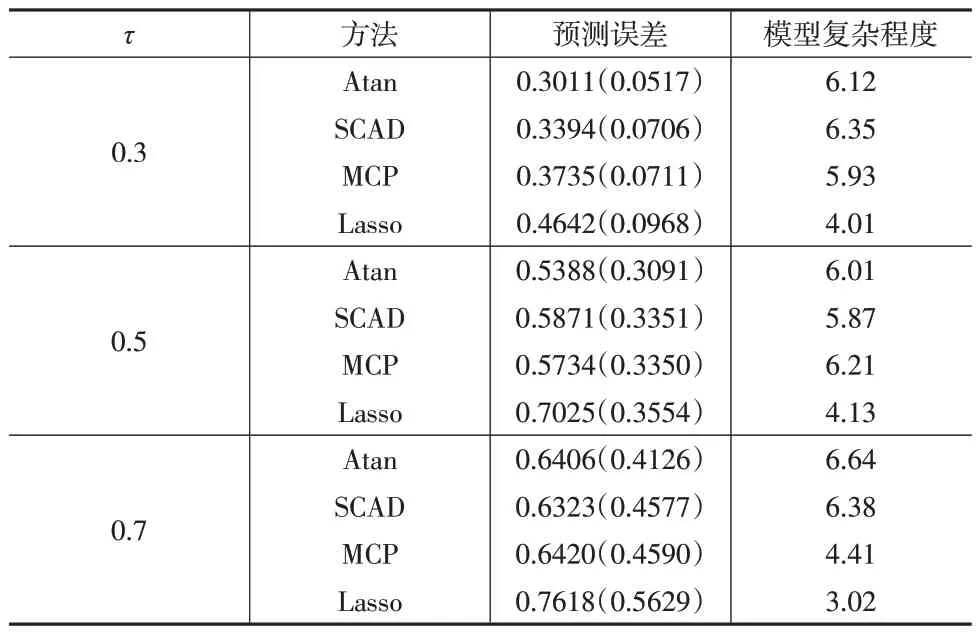
表5 模型拟合和预测
6 结论
本文研究了协变量维度pn发散且为超高维情况下的部分线性可加分位数回归模型的变量选择和稳健估计问题。首先,对于模型中的非参数函数,考虑用三次B 样条函数进行拟合。这种方法不仅在计算上十分便捷,而且通常能够提供准确的结果。为了实现超高维线性部分的稀疏性以及非参数函数的光滑性,本文提出一种Atan 双惩罚估计量,并在一定的正则条件下推导了双惩罚估计量的收敛速度和变量选择的一致性。其次,为了解决所提方法中的优化问题,采用了一种迭代坐标下降算法,即使在pn≫n的情况下也能够实现快速收敛。模拟研究表明,当随机误差项服从标准正态分布时,本文所提Atan 双惩罚估计量的MSE 小于其他惩罚的估计量,因为Atan 惩罚估计量是无偏的。值得注意的是,当误差分布存在重尾时,其他惩罚估计量的FDR 逐渐上升,而Atan 双惩罚估计量的伪发现率仍能保持在较低水平,即Atan 方法选择了更精确的模型。最后,将本文提出的方法应用于一个包含315 个癌症筛查病人的血液样本数据的数据集。通过比较不同惩罚下的变量选择结果发现,本文提出的Atan 双惩罚方法在预测精度和标准误方面均优于SCAD 和MCP惩罚,表明该方法更稳定。总体而言,基于Atan双惩罚的选择结果相对理想,是一种相对稳健的惩罚方法。
