整体设计 凸显一致——“分数与除法”的教学新实践

文| 刘士锋，李士娟

在学习整数除法和小数除法时，学生不仅要掌握算法，还要基于计数单位对算理进行表达，也就是初步形成“算理+算法”的知识结构和“基于计数单位对数进行均分”的思维结构。

一、激活已有经验，生成新问题

1.把8 个月饼平均分给4 个人，每人分得几个？

师：怎样列式？结果是多少？

生：8÷4=2（个）

生：就是把8 个月饼平均分成4 份，所以用除法，每份2 个。

2.把1 个月饼平均分给4 个人，每人分得几个？

生：1÷4=0.25（个）

师：你是怎样想的？

生：把1 个月饼平均分给4 个人，每人分不到1个，所以商用小数表示。

师：是的，当每人分不到1 个月饼时，可以用小数来表示。除了用小数表示1÷4 的商外，还可以用什么数来表示呢？

【思考】创设学生熟悉的分月饼情境，引导学生借助已有的“总数÷份数＝每份数”的经验，列出相应的除法算式并用整数或小数表示结果，为后续学习运算的一致性提供素材，同时生成新的问题。

二、数形结合，寻求答案

1.用分数表示1÷4 的商

师：在学习“分数的意义”时，我们有什么经验呢？

生：画图或折一折。

师：那我们先用画图的方法来看一看。

（课件出示画图的过程）

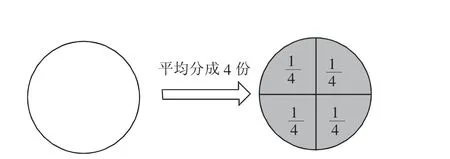
师：看来1 个月饼的几分之几，就是几分之几个。

【思考】在之前“分数意义”的学习中，主要学习了分数对部分和整体关系的表达，缺少用分数表示数量的经验，使得学生对分数意义认识不全面，因此本环节借助画图和分数的意义，除了直观地得到1÷4 的商外，还增加了1 个月饼的几分之几就是几分之几个的表述与理解，初步感悟分数既可以表示关系又可以表示具体的数量，为接下来的研究奠定知识基础。

2.探究3÷4 的商

课件出示：把3 个月饼平均分给4 个人，每人分得几个？

学生借助学具，分一分，折一折，并进行汇报。

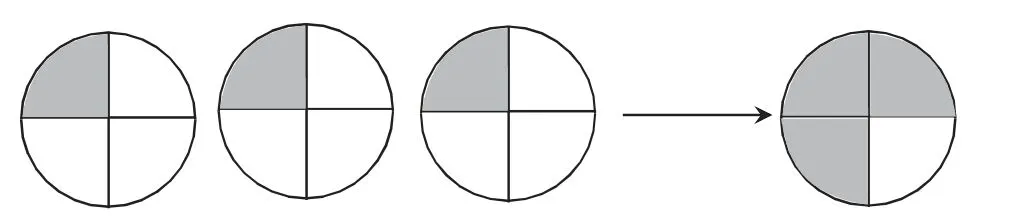
生：把每个月饼都平均分成4 份，分别拿出1 份，每个人就分得3 份，把这3 份拼在一起，就是1 个月饼的，是个，所以3÷4=（个）。

方法2：

【思考】在以往的教学中，本环节通常会让学生解释其中道理，每人分得3 个个，这样学生在描述的过程中非常拗口，通过实践来看，可以帮助学生清晰地理解算理，故而借助操作寻求算式的结果淡化了说理。

3.探究5÷6 的商

出示：把5 个月饼平均分给6 个人，每人分得几个？

师：刚才我们借助画图或折纸的方法分别找到了1÷4 和3÷4 的商，如果我们不画图、不折纸，你能用分数表示5÷6 的商吗？

师：能说一说你是怎样想的吗？

生：我们可以把5 个月饼分别平均分成6 份，每个月饼拿出1 份，拼在一起就是1 个月饼的，是个，所以5÷6=（个）。

生：我们也可以把5 个月饼叠在一起，平均分成6 份，每人分得这样的1 份，然后把它们拼在一起，也得到1 个月饼的，是个。

师：看来同学们很善于利用已有的经验来解决问题，那究竟对不对呢？我们借助图形来验证一下。（出示图形验证答案）

【思考】本环节不再借助具体操作，而是利用前一环节中的单个分或者整体分的研究经验，发挥想象，进行推理，有利于培养学生的推理意识，同时在描述分月饼的过程中进一步加深了理解。

三、观察分析，探寻关系

师：如果把78 个月饼，平均分给99 个人，每人分得几个呢？

师：看来同学们已经有所发现了，我们一起来看一看刚才的研究成果。

师：大家仔细观察，有什么发现？

生：这3 个算式都是整数除法，在计算时，如果商不能用整数表示，就可以用分数来表示。

生：用分数表示整数除法的商时，分子和被除数一样，分母和除数一样。

师：是的，整数除法运算出现不够除的时候，就产生了分数，而且用分数表示整数除法的商时，分子相当于除法算式中的被除数，分母相当于除法算式中的除数。可以这样表示：被除数÷除数=。会用字母来表示它吗？

生：在除法里除数不能是0，还得补充上b≠0。

师：真好，考虑得非常全面。请同学们继续思考两个问题：分数和除法有什么区别？你对分数有哪些新的认识？

生：有区别，除法是一种运算，而分数是一种数，不完全一样。

生：我发现分数除了表示部分和整体的关系，还能表示一个具体的数量、除法计算的商。

【思考】通过观察思考，学生能够发现分数与除法的关系，在此基础上引导学生思考，对分数有了进一步的认识，分数既可以表示部分与整体的关系，又可以表示具体数量和商，从而实现了整数、分数、小数认识的一致性。

四、对比联系，感悟一致性

师：刚才我们通过研究不仅知道了分数与除法的关系，还对分数有了更全面的认识，大家观察下面几个算式有什么新的发现呢？

师：我们先来看8÷4=2，大家能借助计数单位解释其中的道理吗？

生：我来说8÷4，8 表示8 个一，把8 个一平均分成4 份，每份分得2 个一，所以商是2。

师：说得真不错，那剩下的2 个算式中又有怎样的道理呢？比如1÷4=，谁能来说一说？

师：研究到这里，大家有什么想说的？（学生陷入了短暂的沉默）

生：老师，我有发现，后面2 个算式的商都不能用整数表示，这时就可以把几个一平均分，这样一来就变成了几个几分之一，就能用分数表示了。

生：我给补充一下，平均分的时候，就产生了一个新的分数单位，如把1 平均分成4 份，就产生了分数单位，把1 平均分成6 份，就产生了分数单位，这样计数单位小了，但是计数单位的个数增加了，就够分了。

师：同学们的发现太重要了，当商不能用整数来表示的时候，我们可以把大的计数单位，通过平均分产生新的小的计数单位，再进行运算。

师：这两个算式都是计算1÷4，商一个是用小数表示，一个是用分数表示，大家还有什么发现？

生：用小数表示的时候，就是把大的计数单位转化成了0.1 和0.01，用分数表示的时候是把大的计数单位转化成了。

师：大家同意他的说法吗？

生：同意。

生：我还有个疑问，要是这样的话，8÷4 的商是不是也可以用分数来表示？

师：提出一个问题比解决一个问题更有价值。那8÷4 的商能不能用分数来表示呢？

师：理解得真透彻。我们一起来梳理一下，这些除法算式都是把什么进行平均分的？

生：计数单位。

生：可以根据需要把计数单位进行转换。

师：是的，整数除法无论是用整数、小数还是分数来表示商，均分的都是计数单位，它们是一致的。通过对数的认识的学习，我们知道数是对计数单位个数的表达，现在看来数的认识和数的运算都是以“计数单位”为核心的。

【思考】在借助操作探寻出分数与除法的关系后，进一步引领学生从“计数单位”的角度，对除法算式进行算理的解释，这样学生在激活已有用整数表示商的基础上，结合操作获得直观经验，发现在平均分的时候，产生了新的计数单位（分数单位）。在不改变数的大小的前提下，通过把计数单位进行细分获得新的小的计数单位，这样新计数单位变小的同时，增加了新计数单位的个数，使得除法计算得以进行，而且通过对8÷4 的商既可以用整数表示又可以用分数表示的对比，让学生深刻体会到用分数表示商的通用性。