小学数学“问题解决”教学模式的实践探究
——以人教版五年级“多边形的面积”为例
2024-05-25熊晓岚
文| 熊晓岚
在小学数学教育中,面对以形象思维为主导的小学生群体,如何激发他们的学习兴趣,培养他们的逻辑思维和问题解决能力,成为每位教师面临的挑战。传统的“口耳相传”与“题海战术”虽然短期内可能带来成绩的提升,但长远来看,这种机械化的学习方式抑制了学生的创造性和探索精神。而随着“问题解决”教学模式的提出,打破了这一僵局。它鼓励教师从生活实际出发,设计富有启发性的问题,使学生在解决问题的过程中,不仅能锻炼逻辑思维,还能深切感受到数学与生活的紧密联系。这种教学模式让学生成为学习的主体,激发他们的主动性和创造性,培养他们独立思考和解决问题的能力。
一、小学数学“问题解决”教学模式概述
(一)“问题解决”教学模式的概念
小学数学“问题解决”教学模式是一种以学生为中心,以实际问题解决为导向的教学方法,它强调将数学教学内容与实际生活情景相结合,让学生在解决问题的过程中学习数学,发散数学思维,并提升问题解决能力。在这种教学模式下,教师不再是单纯的知识传授者,而是学生学习过程中的引导者和协作者,通过设计具有挑战性和启发性的问题,引导学生通过观察、思考、猜测、交流和推理等富有思维成分的活动,发现数学问题,分析数学关系,提出解决方案,并进行验证。这种教学模式旨在培养学生的数学意识、逻辑思维、创新精神和合作能力。“问题解决”教学模式的核心在于问题的设计和解决过程。问题应该具有现实意义和趣味性,能够激发学生的学习兴趣和好奇心。解决过程则强调学生的主动性和合作性,鼓励他们通过自主探索和小组讨论来找到问题的解决方案。
(二)“问题解决”教学模式的价值
“问题解决”教学模式在小学数学教学中展现出极高的价值。它鼓励学生主动参与到问题的发现、分析和解决过程中,从而培养学生的主动学习与探究精神。通过将数学知识与实际生活情景相结合,这种教学模式不仅增强了学生的数学应用意识和能力,还使他们在解决问题的过程中体会到数学的实用性。此外,学生在解决问题的过程中需要深入思考和推理,这有助于培养他们的数学思维能力,同时鼓励他们发扬创新精神,尝试不同的解决方案,进而提升创新能力。值得一提的是,该教学模式还强调学生之间的合作与交流,这不仅提升了他们之间的沟通与合作能力,还培养了他们的团队合作精神。
二、“问题解决”教学模式在小学数学教学中的应用策略
(一)借助生活实际,实现教学内容的与时俱进
随着时代的进步和科技的发展,学生所接触和生活的环境也在不断变化。为了使学生能够更好地应用数学知识解决实际问题,并激发他们的学习兴趣,数学教师需要时刻关注学生的生活实际,将最新的生活元素融入教学内容中。例如,利用现代科技,如智能手机、电子支付等,设计与学生日常生活紧密相关的数学问题。这样,学生不仅能感受到数学与生活的紧密联系,还能在解决问题的过程中,体验到数学知识的实用性和趣味性。同时,教师还可以根据社会热点和时事新闻,设计与之相关的数学问题。这样,学生不仅能学到数学知识,还能培养关注社会、关心时事的好习惯。这种与时俱进的教学内容设计,能使学生更加愿意参与数学学习,更加主动地应用数学知识解决生活中的实际问题。
例如,在人教版小学数学五年级“多边形的面积”的教学中,为了使学生更好地理解和应用多边形面积的计算方法,教师可以运用“问题解决”教学模式,并结合学生的生活实际来设计具体的教学案例。
案例背景:学校准备为学生修建一个新的多功能运动场,该运动场由多个不同形状的区域组成,包括长方形、正方形、三角形和梯形等。为了预算建设成本,学校需要计算每个区域的面积。教师提出问题:如何帮助学校计算这些不同形状区域的面积呢?教师引导学生思考:
1.如何确定每个区域的形状和尺寸?
2.如何使用测量工具(如卷尺、激光测距仪等)来测量每个区域的边长和高?
3.如何计算长方形和正方形的面积?(长方形面积=长×宽,正方形面积=边长×边长)?
4.如何计算三角形和梯形的面积?[三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2]
学生可以选择分组讨论,每组选择一种形状的区域进行计算,计算完成后分享计算结果,并讨论不同形状区域面积计算的异同点。在完成这个案例后,教师可以引导学生思考如何将多个不同形状的区域面积相加,得到整个运动场的总面积。教师还可以让学生自行设计一个小型运动场模型,并计算其各个区域的面积及总面积。通过这个教学案例,学生不仅能够掌握多边形面积的计算方法,还能够将所学知识应用于解决实际问题中,通过参与讨论、计算和分享,提高自己的思维能力和解决问题的能力。同时,学生设计运动场模型还能够发挥创造力,将数学知识与实际生活相结合,实现知识的迁移与应用。
(二)科学设定教学目标,实现学生学科核心素养的培养
在小学数学教学中,应用“问题解决”教学模式的首要方法是科学设定教学目标,不仅要涵盖数学基础知识的掌握,还要注重学生学科核心素养的培养,学科核心素养包括但不限于学生的数感、空间观念、数据分析观念、运算能力、推理能力等。教师在设定教学目标时,需要明确每项核心素养的培养目标和阶段,确保教学内容和方法与学生的认知发展相匹配。在问题的解决过程中,学生可以亲身体验到数学知识的应用价值,进而提高他们的学习兴趣和主动性,促进学科核心素养的全面发展。
例如,在讲解“多边形面积”内容时,为提高教学效率,教师可以设计一系列与多边形面积计算相关的问题,帮助学生巩固所学知识,并将学生的空间思维、逻辑推理和问题解决能力等学科核心素养的培养融入问题设计中。
活动一:基础练习
在平行四边形中,已知其两个底和一个高的长度,求图1 的面积。
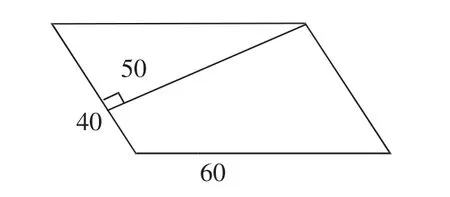
图1
在本题中,已经给出了三个量,分别给出了两个底和一个高的长度,要想用平行四边形面积公式,就要确定出高与哪条底是对应的,然后用对应的底和高相乘,求出平行四边形的面积,最后可以得出40×50=2000(cm2)。所以这个平行四边形的面积为2000cm2。
活动二:挑战提升
教师还可以展示更复杂的多边形,要求学生尝试计算面积。学生可以先独立思考,然后小组讨论,最后分享解题思路和答案。
如图2 所示,一个大梯形里包含一个梯形和一个三角形。已知大梯形的上底AE 为5cm,下底BD为9cm,高AB 为4cm。同时,小梯形的面积与右边三角形的面积相等,求三角形的底是多少?
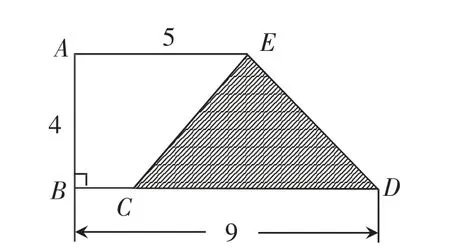
图2
根据题意,我们可以推断出三角形的面积是大梯形面积的一半。首先,需要计算大梯形的面积。根据梯形面积的计算公式,梯形面积=(上底+下底)×高÷2,代入已知数值,得到大梯形的面积为(5+9)×4÷2=28cm2。因为小梯形的面积与三角形的面积相等,所以三角形的面积是28÷2=14cm2。接下来,需要利用三角形的面积计算公式来求出三角形的底。三角形面积=底×高÷2,由于三角形的高为4cm,可以通过等式变换求出三角形的底。设三角形的底为xcm,则有4x÷2=14cm2。解这个等式,得到x=14×2÷4=7cm。因此,根据题目条件和数学计算,可以得出三角形的底是7cm。这个解题过程不仅能帮助学生理解多边形面积的计算方法,还能让他们深刻体会到等式性质在实际问题中的应用,通过独立思考、小组讨论和分享答案,学生能够更加深入地理解和掌握这些知识点。
(三)因材施教,实现问题解决的多样化
由于学生具有不同的数学基础和学习能力,教师应根据学生的个体差异,为他们量身定制适合的学习任务。这种个性化的教学方法不仅有助于激发学生的学习兴趣和动力,还能使学生根据自身的实际情况,对所学知识进行深入理解和掌握。同时,教师应鼓励学生采用多样化的方法来解决数学问题,因为不同的解题方法能够培养学生不同的创新思维和解决问题的能力。教师可以引导学生从不同角度和层面解析数学习题,帮助学生开拓解题思路,提高他们的解题能力。
在教授“多边形面积”这节课时,如图3 所示,王大伯想要围成一个鸡圈,他利用了一面墙和一段篱笆。这个鸡圈的形状是一个多边形,已知篱笆的全长是11.5m。
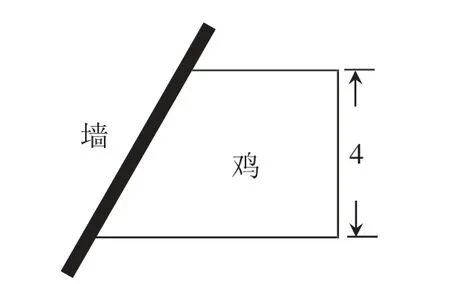
图3
教师可以提出一个探究问题:“如何计算这个多边形鸡圈的面积?”鼓励学生思考不同的解题方法。
由于学生的数学基础和思维方式不同,他们可能会提出多种不同的解题方法。有些学生可能会直接应用多边形面积的公式进行计算,而有些学生可能会尝试通过分割、旋转或平移等方式将多边形转化为已知面积的图形,从而间接计算其面积。
在这个案例中,学生观察鸡圈的形状可以发现,该鸡圈属于矩形性形状,由三个篱笆与墙面共同组成。根据梯形面积计算公式S=(上底+下底)×高÷2 可知,在该鸡圈中,上底和下底分别为篱笆的两端,高为篱笆的另外一端,在计算鸡圈的面积时,学生只需要测量出篱笆的三边就能得出对应的数据,经过计算后,最终可以得出鸡圈的面积。
“问题解决”教学模式的应用,使得学生的探究方法变多了,思路变开阔了,解决问题的路径变丰富了。每个学生都可以根据自己的思维方式来解决问题,而不仅仅局限于一种方法。同时,教师在课堂教学中可以设置讨论环节,让学生在合作中探究,分享自己的解题方法,听取他人的思路,并尝试将不同的方法进行比较和优化。
这样,学生可以详细了解同一个问题的多种解决方法,在提高解决问题能力的同时,还能发散思维,不仅学会了如何计算多边形面积,还学会了如何从不同角度思考问题,如何运用创造性思维来解决问题;不仅提高了学生的数学核心素养,还激发了他们的学习兴趣和动力,为他们的全面发展奠定了坚实的基础。
三、总结
在小学数学“问题解决”教学模式的实践探究中,学生展现出极高的学习热情和解决问题的能力,在面对各种数学问题时,能够积极思考、主动探究,并尝试用不同方法找到答案。这种教学模式不仅让学生掌握了数学知识,还培养了他们的逻辑思维和创新能力。未来,随着“问题解决”教学模式的深入应用,相信学生能够在数学学习中取得更大的进步,为他们的全面发展奠定坚实的基础。
