面向枢纽机场的多因素滑行路径规划综合研究
2024-05-24祁欣月陈长煜
祁欣月, 张 汛, 陈长煜, 张 涛
(1.西藏大学工学院, 拉萨 850000; 2.96951部队, 北京 100085)
随着我国民航业迎来跨越式发展,机队规模日益庞大,机场地面的交通拥堵成为制约航空运输效率的“瓶颈”,枢纽机场作为中枢航线网络的节点,面临更大的挑战。这种状况导致机场资源利用不充分,同时加剧了航班延误和废气排放等问题。扩大机场容量、完善基础设施建设是最直接的解决方案,但考虑成本和机场环境,短时间内扩建不现实。为此,从航空器路径规划和减少燃油消耗两方面入手,针对场面资源中滑行道容量不足问题,在避免冲突基础上进一步缩短航空器滑行距离,可以在一定程度上缓解这一问题。
国内外学者在航空器路径规划方面展开了大量研究。刘帆等[1]提出了场面滑行动态规划的A*算法,建立航空器总体滑行耗时最短、延误最少的动态优化模型,减少了航空器总体滑行时间。张兆宁和余州[2]基于态势感知对滑行路径进行优化,在传统的先到先服务算法基础之上,加入了滑行道系统运行态势。黄邦菊和史继龙[3]为解决多航空器之间的冲突问题,以优化后的滑行路径距离作为目标代价函数,提出一种滑动时间窗与遗传算法相融合的冲突解脱模型。姜雨等[4]提出适用于航空器滑行时空协同优化模型的双层规划算法,以降低场面航空器滑行距离和等待时间。彭可欣等[5]通过对机场航班运行管理程序的研究,建立了协调航班移交的整数线性规划模型,优化航班推出时刻及滑行时间,从而减少航班延误。Idrissi等[6]利用决策支持系统为航空器滑行指定一条直达路线并更准确地预测滑行时间,提高场面运行效率。Ali等[7]以预测动态热点作为空侧冲突的预兆事件,在时间和空间维度上模拟飞机到达不同滑行道的交叉口,使用统计学中的时空模型计算已识别交叉口的冲突概率并评估冲突系数及热点值。Xiang等[8]提出了一种基于强化学习方法Q-Learning算法的改进方法,为航空器提供滑行路径引导。Ning等[9]采用改进的A*算法求解滑行路径优化模型,生成无冲突滑行路径及新的滑行轨迹占用时间窗,可进一步减少航空器在场面运行的总滑行时间,从而大幅减少航空器冲突次数,保障机场运行安全。
综上所述,国内外学者在减少机场场面滑行时间,缓解交通压力方面的研究取得了一定的成效,但现有的航空器滑行路径优化算法未能在充分考虑航空公司成本及节能减排效果的基础上提出最优路径。针对机场整体运行效能低下,尤其是滑行道容量不足、解决方式不够全面等关键难题,通过研究枢纽机场高效运行模式、优化航空器总滑行距离来提高整体协同决策,分析航空器滑行规则,依据国内某枢纽机场场面滑行系统实际航图建立模型,保障场面运行安全的前提下考虑经济、环保和公平性原则,重点规划缩短航空器总滑行距离的路径,提高滑行效率,扩大滑行道容量。本文通过对路径优化问题的研究分析,本文基于Dijkstra算法将机场场面滑行路径转换为邻接矩阵,寻找固定起终点的最短路,并利用MATLAB模拟来执行Dijkstra算法。研究内容包括:①建立机场场面资源网络简图,利用计算机辅助设计(computer aided design,CAD) 测量相邻节点间的图上距离,基于Dijkstra算法为多条航空器滑行路径建立邻接矩阵;②对滑行路径进行优化求解,减少滑行距离及时间;③通过减少转弯次数及滑行时间来降低燃油消耗和污染物排放。
1 滑行路径规划算法
1.1 滑行道运行分析
滑行道系统是机场的重要组成部分,是供航空器滑行和连接机场各功能区的通道。滑行道容量在一定程度上影响机场的场面运行效率。图1为某机场滑行道示意图,包括进出口滑行道、主滑行道、机坪滑行道、辅助滑行道及滑行道道肩等。
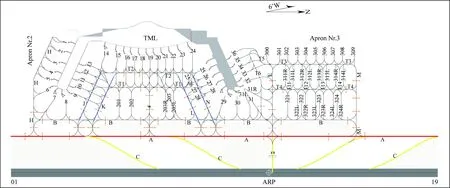
TML表示航站楼;Apron表示相应的停机坪;ARP表示机场基准点;A、B、C等均表示滑行道;数字表示停机位
一般将滑行道冲突分为3类:A交叉冲突、B追尾冲突、C对头冲突。 对头冲突是指同一滑行道上两航空器相向滑行,在某时刻存在碰撞风险,这是滑行过程中最危险的状况,应当各自靠右侧滑行,保持一定距离。此外,针对交叉及追尾冲突,民航局严格规定了不同机型在滑行过程中前后机之间的安全间隔(表1),通过保持安全间隔主动避让或另选滑行路径的方法解脱冲突。

表1 航空器滑行尾流间隔标准
1.2 航空器燃油消耗和排放
在缩短总滑行距离的前提下兼顾场面运行安全、航空公司经济以及环保效能。避免滑行冲突的同时,控制滑行速度并减少转弯次数可有效降低燃油消耗[10]。
根据不同运行模式下的燃油流率和排放指数,采用国际民航组织(ICAO)规定的燃油消耗和废气排放计算方法,公式为
(1)
(2)

当发动机处于怠速时,部分机型的燃油流率及排放指数见表2。

表2 燃油流量及排放指数
1.3 滑行路径规划目标函数
将安全间隔、冲突解脱和公平性原则作为约束条件,建立滑行路径优化模型。采用Dijkstra算法综合考虑飞机的滑行距离、滑行过程中的大转向及避撞情况,最小化飞机的总滑行时间,从而减少滑行阶段的油耗及污染物排放。
(3)
式中:xijf=1表示飞机f通过滑行道节点Ni滑行到下一个相邻节点Nj,否则xijf=0;tijf为飞机f从滑行道节点Ni滑行到下一个相邻节点Nj所用的滑行时间;nf为飞机f在滑行路径上累计转弯的总数;tn为飞机f平均每次转弯所需的时间。
为避免滑行过程中发生冲突,考虑以下约束条件。
(1)滑行道容量限制:
Wisu≤Lsu,∀fi∈F,∀ns,nu∈N
(4)
式中:ns为滑行道起始节点;nu为滑行道终点;F为航空器集合;N为滑行节点集合;Wisu为航空器fi从节点s到节点u的滑行道容量;Lsu=1表示节点s到u之间存在可用滑行路径,否则Lsu=0。约束条件(4)确保航空器fi从起点到终点存在有效的滑行路径且满足滑行道容量。
(2)优先级约束:
(5)
式中:Gf1f2为优先级因子;γfi为航空器fi的优先级。
(3)滑行安全间隔:
L=[lsu/(Tiu-Tis)](Tjs-Tis)
(6)
式中:lsu为节点s与u之间的距离;Tis为航空器fi到达节点ns的时刻;Tjs为航空器fj到达节点ns的时刻;Tiu为航空器fi到达节点nu的时刻。式(6)是为了确保同一滑行道上两架相邻航空器之间保持一定的安全间隔。
(4)滑行冲突约束:
A对头冲突
Xsuf1tuf1-Xsuf2tuf2≥0
(7)
式中:Xsufi为航空器fi从节点s滑行到节点u;tufi为航空器fi滑行到节点u的时刻。
B超越冲突
(Xsuf1tsf1-Xsuf2tsf2)(Xsuf1tuf1-Xsuf2tuf2)>0
(8)
式中:tsfi为航空器fi滑行到节点s的时刻。
航空器在滑行道系统中的冲突如图2所示。

R1~R4表示跑道节点;G3表示停机坪;m、n、k表示滑行道节点
(5)公平性约束:
(9)
式中:Dα为α航空公司产生额外滑行路线的总长度,A为航空公司集合;Pα为α航空公司的数量占总航空公司数的比值;∑Pα为α航空公司航班数累计占总航空数的比值;ε1为Gini系数的参数值(Gini系数可以反映资源分配的公平程度,值越小,分布越平均)。式(9)旨在确保滑行路线长度的公平性。
2 MATLAB仿真与算法流程
2.1 场面滑行仿真
基于国内某枢纽机场的航班数据,使用MATLAB程序模拟来执行Dijkstra的算法。
算法1:

2.2 Dijkstra算法流程
Dijkstra算法用于求解指定两点Vi、Vj间的最短路,或从指定点Vi到其余各点的最短路,是求解非负权值网络最短路问题的最佳方法。若序列Vi-Vj为最优路径,则其任意子集也被定义为最优解[11]。
基于Dijkstra算法的航空器滑行路径规划基本步骤如下。
(1)固定滑行路径起终点。用Xij表示滑行道权值,Xij≥0。若节点Vi与Vj不相邻,则定义Xij=+∞。给起点Vi以P标号,其中P为永久性标号,P(Vi)=0,将剩余节点标注T,T为试探性标号,T(Vj)=+∞。
(2)将P标号的节点与T标号节点划分为两个集合,从T标号的集合中选取任意与P点相邻的节点,对T标号进行如下计算:T(Vj)=min[T(Vj),P(Vi)+Xij]。
(3)比较所有T标号的权值,将最小值定义为P标号,更新两个集合,重复此过程,直到所有节点均为P标号。此时,找到一条权值最小的滑行路径。
3 实例分析
以国内某枢纽机场2018年某日18:00—19:00的实际航班滑行数据为例,基于该机场航图选取T1、T2航站楼两侧跑道、滑行道和停机坪区域,省略部分无关滑行道,并将停机位抽象为6个综合停机坪,构建机场场面资源网络图(图3)。

R1~R19为跑道节点;G1~G6表示不同区域的停机坪;剩余标号均表示滑行道节点;虚线段表示进场;双线段表示离场
该机场跑道实施隔离平行运行模式,采取“固定、单向、顺向、循环”的滑行规则。停机坪区域通过机坪滑行道与普通滑行道和停机位相连接[12]。
利用Dijkstra算法对航班数据进行模拟计算,基于MATLAB仿真得到航空器地面滑行的具体最优路径。考虑不同机型的滑行速度、滑行时间及热点冲突路段,分析不同的冲突类型,划分航空器优先级,采取加权的方法合理规划路径。
首先确定机场场面资源网络图的节点个数和节点间相对距离,见表3。基于该机场航图,利用CAD测量出相邻节点间的图上距离。在实际运用中,可依据比例尺进行换算,不影响算法结论。
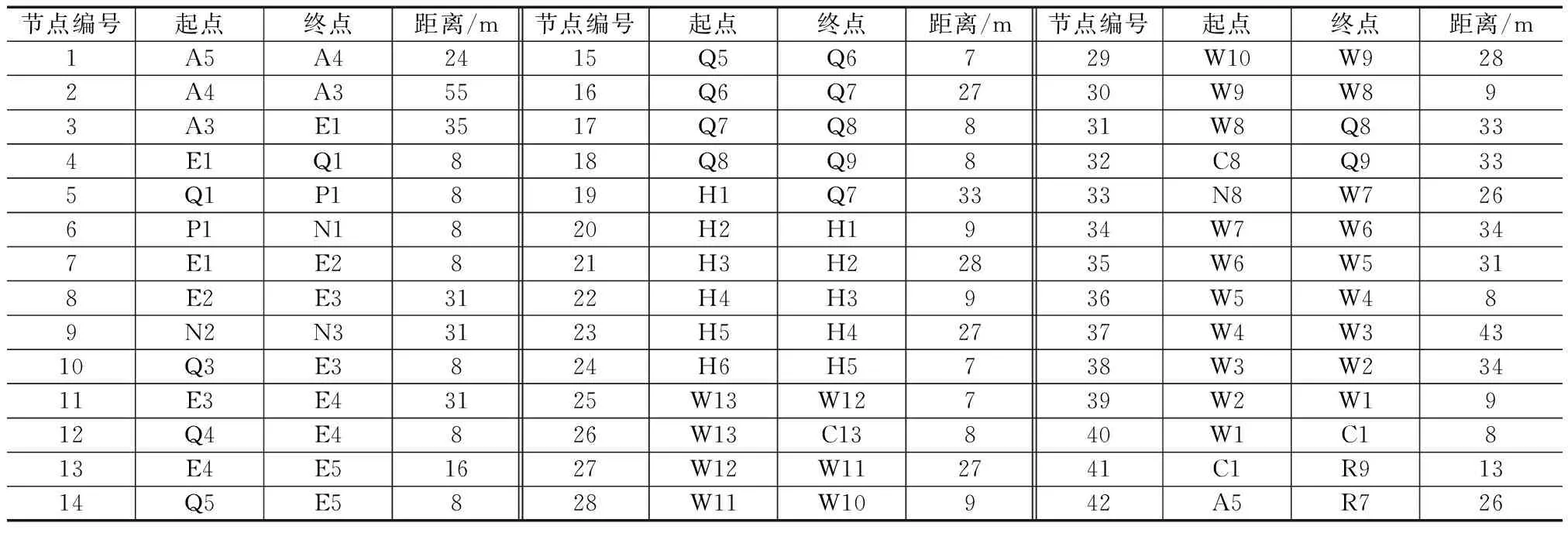
表3 节点距离(部分)
运用Dijkstra算法构建滑行路径起终点间的邻接矩阵,在首次规划不考虑热点冲突及特殊因素的情况下,寻找经过节点数最少、距离Sij及滑行时间Tij最短的滑行路径。飞机时刻表中的最优滑行路径见表4。

表4 滑行路径优化结果
以航班3U8173滑行路径为例,假设E1-E2段因紧急状况暂时关闭,则需另选最短路径。经简化,以Q1为起点,E3为终点不断寻优,由MATLAB最终输出1-3-10,故更新路径为R7-A5-A4-A3-E1-Q1-Q2-E2-E3,路径长度为195 m,滑行时间为234 s。
考虑航空器滑行路径冲突状况,图3中虚线段表示进场,双划线段表示离场。可见,航班CZ6338与HU7268在节点Q6处存在交叉冲突。此时不再运用传统的先到先服务原则,而通过比较优先级以解脱冲突。由于离场航空器相对进场航空器具有绝对优先权,故航班HU7268应选择其他滑行路径或在冲突区域前等待。通过加权的方法为航空器重新规划滑行路径,赋予滑行道不同的权值,假设“100”表示权重上限,分别为停机坪滑行道、联络滑行道、平行滑行道冲突路段赋值80、50、30。故Q5-Q6段距离为57,根据Dijksrta算法重新建立其邻接矩阵,确定其次优路径:R7-A5-A4-A3-E1-Q1-P1-P2-P3-P4-P5-P6-Q6,路径长度为257 m,在有效避免冲突的情况下,与最短滑行路径相比,距离略有增加,在可接受范围内。根据实际滑行距离及该航班滑行速度得出避撞前后滑行时间,显然,两种方案之间仅有17 s时间差,不影响场面运行效率。结果对比见表5。

表5 避撞前后滑行效率结果对比
此外,对比传统A*算法对滑行路径的规划,A*算法[13]是通过比较当前路径栅格邻域的启发式函数值F来确定下一路径栅格,但当存在多个最小值时A*算法不能保证搜索路径最优。A*算法求解15个航班的滑行路径见表6。
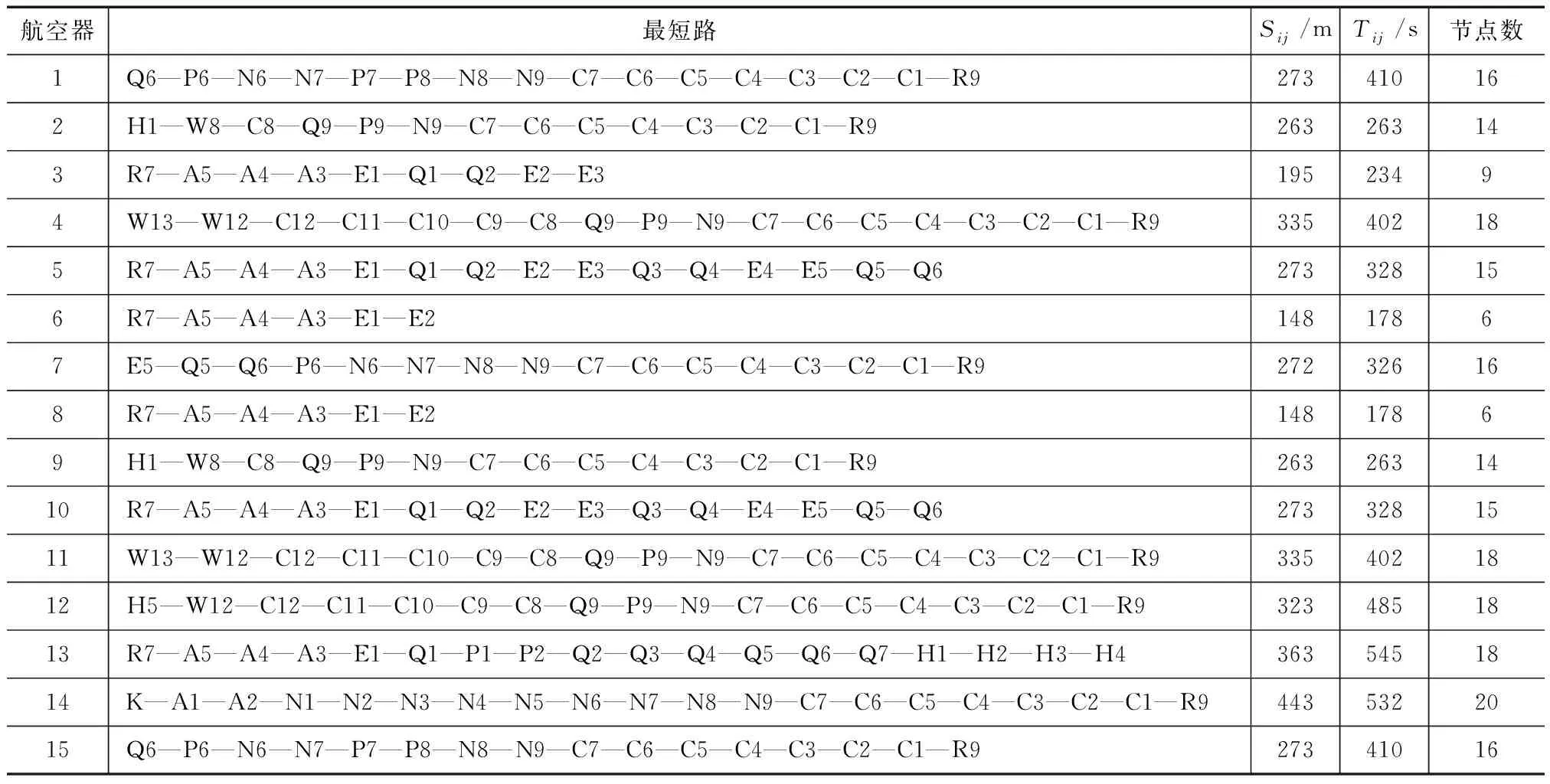
表6 传统A*算法求解滑行路径
对比表4和表6两种算法下的路径规划可知,传统A*算法下15个航班的总滑行距离为4 180 m,总滑行时间为5 284 s,共计转弯44次;Dijkstra算法求解的航空器总滑行距离为4 052 m,总滑行时间为5 115 s,共计转弯25次。
较少的转弯次数及滑行时间有利于降低燃油消耗和污染物排放。根据式(1)、式(2)及部分机型的燃油消耗和排放指数计算两种算法下的航空器滑行油耗及污染物排放总量。图4为15个航空器分别在两种算法求解下的滑行路径油耗量,图5为航空器滑行产生的3种污染物HC、CO及NOx排放总量对比。由图4、图5可知,本文提出的Dijkstra算法在相比传统A*算法油耗总量下降了3.29%,同时3种污染物总量分别减少了3.32%、3.34%、3.28%。枢纽机场繁忙时段航空器起降频繁,采用Dijkstra算法为多架航空器滑行提供合理路径,将显著提升滑行效率,大幅减少油耗及污染物排放。

图4 两种算法求解下15个航空器滑行油耗量对比

图5 两种算法求解下15个航空器滑行产生的3种污染物HC、CO及NOx排放量对比
4 结语
针对机场场面滑行道容量不足问题,构建了滑行路径规划模型,设计了Dijsktra求解算法,并利用国内某枢纽机场航空器地面实际滑行数据进行了验证对比。结果表明,基于Dijsktra算法的路径规划有助于缩短滑行时间从而减少燃油消耗及污染物排放,所提出的模型及算法可行,可显著提升滑行效率。
为保证该算法的鲁棒性,在未来的实际运用中可将机场场面滑行路径以固定的邻接矩阵编入代码中。此外,基于航空器滑行的动态性特点,应充分考虑多方因素,如地面特种车辆对航空器滑行路径的影响等,综合运行现状,确保滑行道容量最大化。
