ARIMA与ARIMAX模型在私人汽车拥有量预测中的应用

张淑娴

(安徽建筑大学数理学院, 合肥 230601)

随着国民经济的持续快速发展,全国私人汽车的拥有量急剧攀升。汽车的广泛普及便捷了人们的生活,但又在一定程度上对环境造成了危害。因此,研究全国私人汽车拥有量对于改善环境具有重要意义。

目前,一些学者对汽车拥有量的影响因素及预测进行了研究。张琪[1]综合考虑了私人汽车拥有量与经济、城市和交通这3种属性之间的关系,分别建立了随机效应模型、固定效应模型与混合回归模型,通过分析发现城镇居民家庭人均可支配收入为私人汽车拥有量的主导因素。周亚林等[2]首先借助机器学习中的极度梯度提升树法识别得到了影响新疆私人汽车保有量的因素,然后比较了极端梯度提升树(extreme gradient boosting,XGBoost)、随机森林和神经网络这3种方法的预测结果,结果表明神经网络预测效果最好。杨昆等[3]采用M-K(Mann-Kendall)检验、Theil指数、线性倾向率和面板数据模型,从全国、8大经济区域、各省3个尺度研究了中国民用汽车拥有量的时空变化特征及其与地区生产总值、公路里程和居民消费水平这3个影响因素的关系,结果表明在不同的时间阶段和空间尺度,各因素对民用汽车拥有量的作用方向以及强度上表现出了差异。Kai等[4]在经典指数曲线模型和修正指数曲线模型的基础上,提出了一种具有一阶多项式项的新型指数曲线模型,将这3种模型的预测结果进行比较,结果显示运用新型指数曲线模型预测中国私家车拥有量具有更高的精度。郭艳莉[5]采用灰色-广义回归神经网络预测模型分析私人汽车拥有量,预测结果表明该模型优于回归预测模型、灰色预测模型和反向传播(back propagation,BP)神经网络预测模型。李炳炎等[6]利用多元线性回归模型和向量自回归(vector autoregression,VAR)模型预测江苏省私人汽车拥有量,结果显示年末总人口数为私人汽车拥有量的主导因素。上述研究大多局限于单变量的时间序列分析。

本文选取2005—2020年全国私人汽车拥有量的相关数据进行实证分析,分别构建基于Lasso和灰色关联分析方法下的差分自回归移动平均模型(autoregressive integrated moving average,ARIMA)模型与动态回归(ARIMAX)模型,分析影响私人汽车拥有量的关键因素,借此进一步预测私人汽车拥有量的变化趋势,以期为汽车数量的有效控制提供依据。值得一提的是,在本文的研究中考虑了多因素影响的ARIMAX模型,其预测效果优于ARIMA模型,能更好地反映各变量之间在时间上的动态关系。

1 模型简介

1.1 Lasso模型

考虑一个具有标准化自变量和因变量的线性回归Y=βX+ε,其中Y=(y1,y2,…,yn)Τ;X=(x1,x2,…,xp),xp=(x1i,x2i,…,xni)Τ,i=1,2,…,p,n为样本的个数;β=(β1,β2,…,βp)Τ,p为解释变量的个数;ε=(ε1,ε2,…,εn)Τ,ε为误差向量且满足E(ε)=0,Cov(ε)=σ2I,I为单位矩阵。

在线性模型的基础上产生的Lasso筛选变量公式为

(1)

(2)

1.2 ARMA模型

自回归移动平均(ARMA)模型[7]是通过自回归模型与移动平均模型相结合产生的,其定义为

(3)

式中:yt为当前序列值;φ0为常数项;p为AR(p)模型的偏自相关系数p阶截尾;φi为自相关系数;q为MA(q)模型的自相关系数q阶截尾;θi为偏自相关系数;εt为随机干扰项;yt-i为t-i时刻的序列值;εt-i为t-i时刻的残差值;φp为p时刻的自相关系数;θq为q时刻的偏自相关系数;εs为s时刻的残差;xs为s时刻(过去)的序列值;s为s时刻(过去时刻);t为t时刻(当期)。

差分自回归移动平均(ARIMA)模型与ARMA模型的区别是ARIMA模型需要对时间序列进行d阶差分,从而得到平稳的时间序列。

1.3 多元时间序列ARIMAX动态回归模型

ARIMAX模型构造之前必须满足响应序列{yt}和输入变量序列{x1t,x2t,…,xkt}均为平稳序列;若不是平稳序列则需要采用差分或对数化的方法使其变平稳,随后便能够构造响应变量与输入变量之间的模型。

ARIMAX模型构造的基本思想[7]为:考虑响应序列{yt}(即因变量序列)与输入变量序列(即自变量序列){x1t,x2t,…,xkt}均平稳,构建因变量序列与自变量序列的回归模型为

(4)

式中:μ为模型常数项均值;B为移位算子;Φi(B)为第i个输入变量的自回归系数多项式;Θi(B)为第i个输入变量的移动平均系数多项式;li为第i个输入变量的延迟阶数;{εt}为回归残差序列。

由于{yt},{x1t},{x2t},…,{xkt}均平稳,那么平稳序列的线性组合仍然是平稳的,也就是说残差序列{εt}是平稳序列,{εt}的表达式为

(5)

接着借助ARMA模型继续提取残差序列{εt}中的相关信息,最终得到的模型称为动态回归模型,简记为ARIMAX。该模型表达式为

(6)

式中:Φ(B)为残差序列的自回归系数多项式;Θ(B)为残差序列的移动平均系数多项式;at为零均值白噪声序列。

2 变量筛选

选取国家统计局提供的数据进行归纳整理,将全国私人汽车拥有量看作被解释变量,居民消费价格指数、公路里程等8个因素看作解释变量进行分析,见表1,并基于Lasso和灰色关联分析方法筛选影响私人汽车拥有量的关键因素。

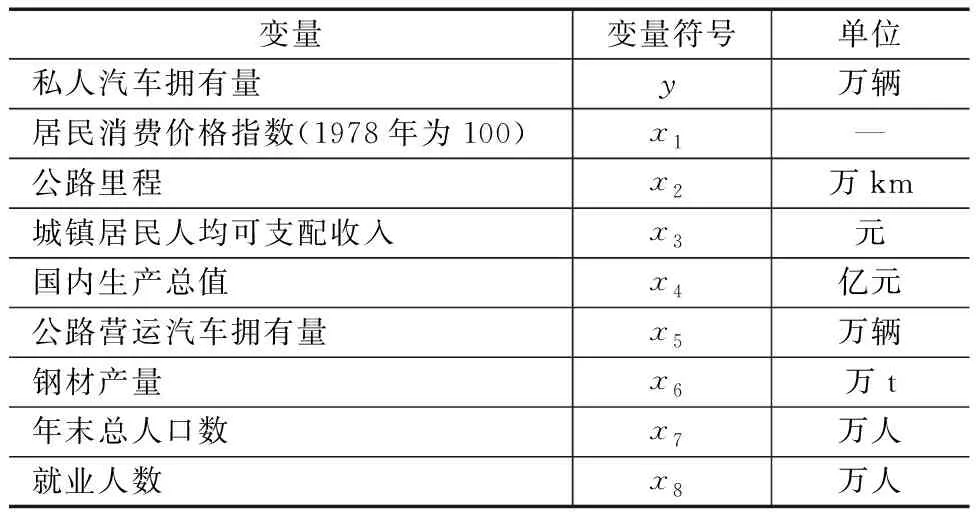
表1 影响私人汽车拥有量的变量选取及其含义

2.1 Lasso筛选关键因素

通过R语言中的glmnet函数对私人汽车拥有量和8个影响因素的数据构建Lasso回归模型。压缩系数λ的取值不同,模型的系数变化不同,图1中每一条曲线的变化代表每个变量的回归系数随λ变化的趋势。

图1 模型的回归系数值随着压缩系数的变化趋势

在图1中,横坐标表示压缩系数λ的对数值lgλ,纵坐标表示模型的回归系数值。图形顶部的数字表示在对应的λ下得到的非零系数的个数。结果显示模型系数随着压缩系数λ值而变化,变化越来越平稳,最终模型系数趋近于一个相同的值。说明只要找到相对合理的λ值,就能够筛选出有效准确的变量。因此运用交叉验证方法选取最优参数λ值,结果如图2所示。

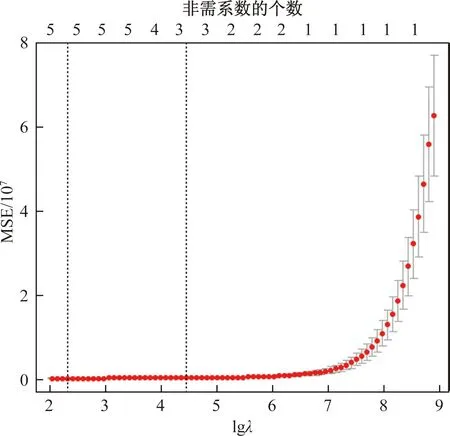
图2 模型的压缩系数与均方误差MSE的变化

在图2中,横轴表示压缩系数λ的对数值lgλ,纵轴表示模型均方误差(MSE),结果显示压缩系数lgλ越小,均方误差越稳定,左侧虚线表示在均方误差最小时所对应的模型包含了5个变量,右侧虚线表示在一倍标准误(SE)内更简洁的模型,包含了3个变量。

最终,Lasso从所有变量中筛选出x3(城镇居民人均可支配收入)、x5(公路营运汽车拥有量)、x8(就业人数)3个变量,其他的变量则被压缩至0。这就说明城镇居民人均可支配收入、公路营运汽车拥有量、就业人数主要影响着私人汽车拥有量的变化。

借助R软件作参数估计,由表2可知,得到变量x8的检验P值为0.298,大于显著性水平α=0.05,故没有通过检验,所以在后续研究中剔除变量x8,只保留变量x3、x5。

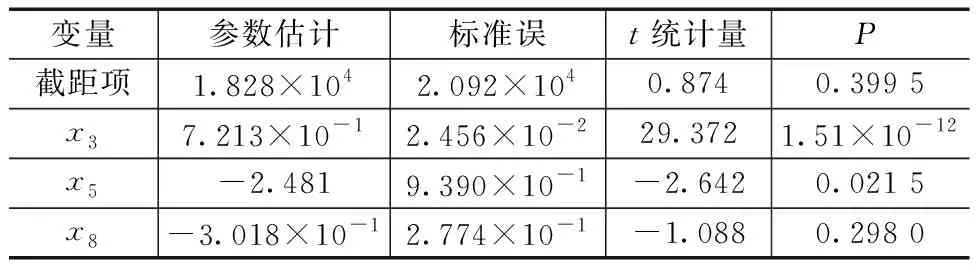
表2 Lasso回归模型参数估计

2.2 灰色关联分析法筛选关键因素

灰色关联分析法可以用来衡量变量之间发展趋势的相近或相异程度,故用此分析方法有利于筛选出影响私人汽车拥有量的因素。此外,灰色关联度的大小代表着各个序列影响主序列的程度大小,有利于分析变量的动态历程。

(1)将私人汽车拥有量作为主序列X0={x0(1), … ,x0(k)},k=1,2,…,16,将居民消费价格指数等8个因素作为影响序列Xi={xi(1),xi(2),…,xi(k)},i=1,2,…,8;k=16。

k=1,2,…,16;i=1,…,8

(7)

式中:ρ为分辨系数,ρ∈(0,1),一般取0.5。

(4)计算全国私人汽车拥有量与各影响因素之间的灰色关联度γoi。

(8)

根据计算步骤,借助MATLAB软件编程求解,得到各相关因子与私人汽车拥有量的灰色关联度,并从大到小排序,结果见表3。

表3 灰色关联度排序

根据灰色关联度排序结果可知,在0.5的分辨系数下,这8个因素对私人汽车拥有量的影响程度为:国内生产总值>城镇居民人均可支配收入>居民人均消费价格指数>钢材产量>公路里程>公路营运汽车拥有量>年末总人口数>就业人员。

对比以上两种方法,筛选出更加完善的影响汽车拥有量的关键因素,其中包括国内生产总值、城镇居民可支配收入和公路营运汽车拥有量。

3 模型建立

3.1 用ARIMA模型预测私人汽车拥有量

借助Eviews软件进行ADF检验(augmented Dickey-Fuller test)可知{yt}是非平稳序列,但对数化后的序列能够通过ADF检验,说明{lnyt}是平稳序列。考察对数化后序列的自相关图与偏自相关图的性质并结合AIC(Akaike information criterion)准则进行定阶,构建模型ARIMA(1,0,2),该模型的AIC值为-26.45,表达式为

lnyt=8.757 5+0.987 2lnyt-1+εt+1.638 2εt-1+εt-2

(9)

下面利用LB(Ljung-Box)检验对残差序列进行检验,当显著性水平α=0.05时,由图3的结果分析发现,有95%以上的标准化残差都是在区间[-2,2]以内的,此外,ARIMA(1,0,2)模型的残差的自相关函数在0阶后迅速下降至上下两条虚线之中,总体上Ljung-Box统计量的P值都大于显著性水平,表明该模型已充分提取信息。参数检验的结果亦显示模型的参数具有统计学意义。因此,可以判定建立的ARIMA(1,0,2)模型是合理的。

图3 ARIMA(1,0,2)模型残差诊断检验

可以利用该模型对原始时间序列作预测,预测2021年、2022年的私人汽车拥有量数据。

3.2 用ARMAX模型预测私人汽车拥有量

由于序列{yt}、{x3t}、{x4t}、{x5t}均未通过ADF检验,所以它们是非平稳序列,考虑将这4个序列对数化可以使它们变平稳,然后借助Eviews检验对数化之后的序列是否平稳。

将城镇居民人均可支配收入、国内生产总值和私人汽车拥有量这3个因素对数化后可表示为{lnx3t}、{lnx4t}、{lnyt}。采用Eviews中的ADF检验可以得到检验P值分别为0.014 5,0.021 8,0.045 7,它们均小于显著性水平α=0.05。由此可知{lnx3t}、{lnx4t}、{lnyt}这3个序列具有稳定性。然而{lnx5t}与{lnyt}非同阶单整,所以剔除序列{lnx5t}。

由于涉及的自变量个数比较多,变量之间也可能会产生多重共线性,如果仅仅使用线性回归来分析输入变量与响应变量之间的关系,就会影响到参数估计的精确度。因此,利用转移函数的结构形式来构建模型能够避免发生以上问题。下面借助R软件的forecast程序包中的arima函数来对输入变量定阶:得到{lnx3t}的拟合模型是AR(1),AIC值为-18.4;{lnx4t}的拟合模型是AR(1),AIC值为-12.07;对残差序列进行LB检验的结果为P值均显著大于显著性水平α=0.05,这表明模型拟合效果好。

对城镇居民人均可支配收入对数化后建立如下拟合模型:

lnx3t=9.981 5+0.989 2lnx3t-1+εt

(10)

对国内生产总值对数化后建立如下拟合模型:

lnx4t=12.999 2+0.988 46lnx4t-1+εt

(11)

根据图4绘制的{lnyt}与{lnx3t}、{lnx4t}的互相关图可知,序列在滞后阶数为0时相关系数最大,说明延迟0阶时最相关,可以同期建模。

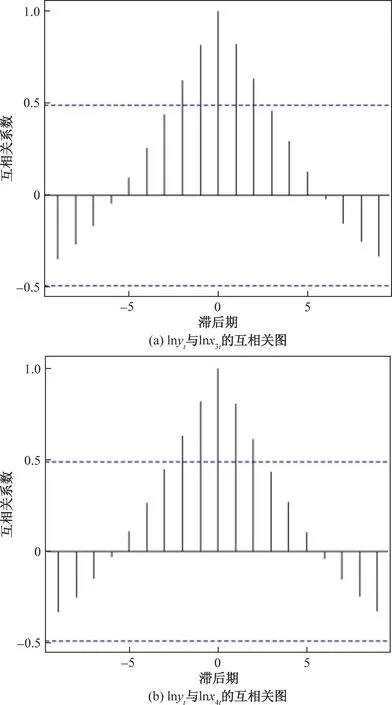
图4 互相关图

将上述关于城镇居民人均可支配收入与国内生产总值的两个模型作为输入变量模型运用到ARIMAX模型中,借助R软件中的TSA程序包里的arimax函数便于拟合ARIMAX模型。结果显示拟合后模型的AIC值为-54.59,那么ARIMAX模型的拟合精度高于没有考虑到影响因素的ARIMA模型。通过LB检验得到的残差序列的P值大于显著性水平α=0.05。说明模型信息已提取充分。此外,利用条件最小二乘法估计模型参数,检验结果显示各参数亦均有统计学意义,即模型显著有效。该模型表达式为

(12)

3.3 模型预测比较

利用上述建立的ARIMAX模型对测试集(2021年、2022年)的全国私人汽车拥有量进行预测,并与ARIMA模型进行对比分析,结果见表4。

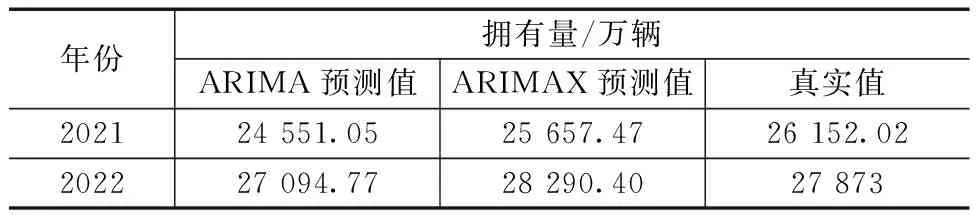
表4 2021年、2022年全国私人汽车拥有量预测结果

表5 2021年、2022年不同方法的相对误差

由表4可知,ARIMAX模型的预测值更接近于真实值。ARIMAX模型的AIC值为-54.59,ARIMA模型的AIC值为-26.45,通过相对误差对预测效果进行定量评估可知,ARIMAX模型的相对误差更小,因此,ARIMAX模型的预测精度要高于ARIMA模型。

4 结论

以2015—2020年全国的私人汽车拥有量数据为基础,利用Lasso回归和灰色关联分析方法综合筛选了变量,结果表明公路营运汽车拥有量、城镇居民人均可支配收入和国内生产总值是影响全国私人汽车拥有量的3个关键因素;随后将它们作为输入变量引入到模型中,分别构建了ARIMA模型与多因素影响的ARIMAX模型来对私人汽车拥有量进行预测。借助R软件对ARIMA模型进行参数估计与残差检验,结果显示建立的ARIMA(1,0,2)模型是合理的。由于私人汽车拥有量与城镇居民人均可支配收入、国内生产总值均在滞后阶数为0时相关系数最大,可以同期建立ARIMAX模型,利用LB检验对模型的残差序列检验通过,说明建立的ARIMAX模型有效。

从实证分析结果来看,ARIMAX模型具有更小的AIC值,预测结果的相对误差也更小,即ARIMAX模型的预测精度优于ARIMA模型,更适用于私人汽车拥有量的预测。通过该模型对未来私人汽车拥有量进行预测,能够为汽车产业的未来经营和发展提供依据。在未来的研究中,还可以进一步考虑将基于定量分析与政策定性分析相结合,从而实现更科学的预测。